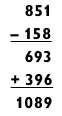в чем магия математики
Матемагия
Как известно, наука творит чудеса. А царица наук — математика. Пусть даже расхожий тезис, будто бы во всякой дисциплине есть ровно столько науки, сколько в ней есть математики, чересчур категоричен, нельзя не признать: она проникает в самые разные отрасли знания, и даже самым махровым гуманитариям порой никуда без её методов, компьютерная лингвистика не даст соврать. Со времён античности и Платоновской Академии, куда «Не геометр да не войдёт», и до наших дней пиетет перед алгебраическими и прочими подобными операциями только увеличивался — особенно в последнее время, с растущей крутизной вычислительных технологий.
И, само собой, людям не могла не закрасться в голову мысль, что числом может быть выражено вообще всё. Не только количественные отношения наподобие габаритов, стоимости, числа аллелей и атомного веса — а совсем уж абстрактные понятия, вроде эмоций, души, жизни, Вселенной и всего остального. А там уж рукой подать до следующего логического (или хотя бы кажущегося таковым) хода: а вот бы найти формулу, по которой эти вещи можно менять. Чтобы сама реальность трансформировалась вместе с вычислением! Хотя, конечно, при наличии таких формул стоит забыть о праве на ошибку. И, конечно, лучше даже не задумываться, что будет, если случайно поделишь на ноль.
Знакомьтесь, перед вами матемагия — богатая родственница нумерологии, ухитрившаяся выбить жилплощадь в НФ и родственных направлениях. Представляет собой нечастый, но весьма эффектный прикладной флеботинум, позволяющий вводить во вроде как наукобразный сеттинг совершенно дичайшие вещи.
Nota bene: нас интересуют только те случаи, когда всякие интересные эффекты достигаются путём целенаправленных вычислений и построений. Когда между двумя и тремя затесалось число Тета, а дважды два на полном серьёзе равно пяти — это не сюда, ибо уже чуждая математика. Кроме тех случаев, когда чудесатые чиселки и формулки используются вместо заклинаний.
Надтроп: Чему б ни учился — опять колдун получился. В нормальной науке тоже есть важные числа, самое известное из них — Пи. Также см. нумерология.
В чем магия математики
Магия математики: Как найти x и зачем это нужно
Переводчик Д. Глебов
Научный редактор А. Чижова
Редактор В. Потапов
Руководитель проекта А. Василенко
Корректор С. Мозалёва
Компьютерная верстка А. Абрамов
Дизайн обложки Ю. Буга
В оформлении обложки использованы изображения из фотобанка shutterstock.com
© Arthur Benjamin, 2015
Публикуется с разрешения издательства BASIC BOOKS, an imprint of PERSEUS BOOKS LLC. (США) при содействии Агентства Александра Корженевского (Россия)
© Издание на русском языке, перевод, оформление. ООО «Альпина Паблишер», 2016
Все права защищены. Произведение предназначено исключительно для частного использования. Никакая часть электронного экземпляра данной книги не может быть воспроизведена в какой бы то ни было форме и какими бы то ни было средствами, включая размещение в сети Интернет и в корпоративных сетях, для публичного или коллективного использования без письменного разрешения владельца авторских прав. За нарушение авторских прав законодательством предусмотрена выплата компенсации правообладателя в размере до 5 млн. рублей (ст. 49 ЗОАП), а также уголовная ответственность в виде лишения свободы на срок до 6 лет (ст. 146 УК РФ).
Эту книгу я посвящаю своей жене Дине и нашим дочерям – Лорел и Ариэль
Математику уже затем учить надо, что она ум в порядок приводит.
Не люблю длинных предисловий. Хочется сразу начать читать книгу. Но здесь не совсем обычная книга. Кажется, что слово «магия» предполагает некоторые фокусы и трюки. Не скрою, они здесь есть, и многим это понравится. Правда, книга не об этом.
Мы задаемся вопросом, зачем нам нужна математика. Особенно гуманитариям. Мой личный опыт научил меня определенному отношению к этому вопросу. Навыки математического мышления оказались нужны всем и каждому. Если вы, конечно, любите размышлять, а не зубрить. Если вам доставляет удовольствие сам процесс логических рассуждений. Парадокс именно в том, что магия, волшебство математики проявляется постепенно, как рассвет. Не сразу, но заметно. Не ярко, но очень красиво.
Вдруг вы замечаете у себя умение логически мыслить и рассуждать, грамотно и четко формулировать мысли, делать верные логические выводы. Вдруг вам просто становится после этого легче общаться с людьми.
Особенно математика важна для развития ребенка. Она дает возможность сразу правильно и рационально мыслить. Причем навсегда. Мне повезло в жизни. У меня было два прекрасных преподавателя. Оба стали моими Учителями. Один преподавал язык и литературу и утверждал, что, «не зная грамматики – не выучишь математики». Второй преподавал математику и «приводил в порядок наши мысли». Они крепко дружили между собой. И, похоже, они считали оба эти предмета волшебно полезными для нашей жизни. Одно оказалось неотделимо от другого. Особенно сильно это проявилось позднее, когда я стал играть (иногда небезуспешно) в различные интеллектуальные игры. Вот такая магия получилась.
Мозг требует таких же тренировок, как и любая другая мышца человеческого организма. Когда-то, лет 30 назад, я работал в Федерации бодибилдинга, как смешно это ни звучит. Должен заметить, что тогда меня сильно удивило интеллектуальное развитие спортсменов, особенно занимающих призовые места на самых престижных турнирах. Оказалось, что для подготовки надо быть почти кандидатом медицинских наук. Ну а когда человек начинает читать разную литературу, его любопытство направляет ум в самые невероятные места. Призер «Мистер Олимпия» Олег Отрох специально занимался математикой. Она помогала ему добиться нужной концентрации. Кроме того, он был убежден, что математика защищает его разум от всяких Паркинсонов и Альцгеймеров. Роберт Фишер – между прочим, чемпион мира по шахматам – научился читать и писать только потому, что иначе он не мог записывать шахматные партии, как того требовали правила. И вот тут он открыл для себя, как помогает ему мыслить математика. Не мог оторваться до последних своих дней.
Вы еще задаетесь вопросом, зачем вам нужна математика? Особенно гуманитариям? Выходит, не только сдачу в магазине считать. Мой личный опыт научил меня определенному отношению к этому вопросу. Навыки математического мышления оказались нужны всем и каждому. Вся эволюция человека от узелков на веревочках и абака до суперкомпьютеров прошла рука об руку с математикой. Даже просто оценивая картину в музее или памятник на улице, мы подсознательно обращаем внимание на пропорции. Благодаря математике мы умеем видеть красоты мира и природы. Каждый раз, выбирая смартфон или компьютер, мы невольно оперируем математическими терминами. Мы гордимся своими селфи, произнося слово «мегапиксели» как заклинание. Вот такая математика. Она не только делает нас разумнее, тренирует наш мозг, развивает нас как личность. Она просто помогает нам жить.
А магия? А что магия? Магия в книге есть. Забавная, замечательная, необыкновенная и неожиданная. Причем даже для тех, кто полагает, что знает эту самую математику. Хочется, чтобы вы ее тоже увидели своими глазами. Увидели и насладились. Это очень красиво.
P.S. А парочку фокусов и трюков я все-таки запомнил.
Всю мою жизнь меня тянуло к магии. Не счесть, сколько кудесников видел я на своем веку, как и не счесть, сколько чудес я сотворил собственными руками. Но я не перестаю восхищаться тем, как работает магия, как из простых и понятных вроде бы действий и алгоритмов вдруг рождается поразительное, непостижимое искусство – искусство, которое я так обожаю постигать. Несколько основных принципов – и вот я уже сам придумываю трюки.
Примерно то же чувство я испытываю, когда дело касается математики. С самого детства шестым чувством я ощущал, что в числах кроется истинная магия. Как вам, например, вот это? Задумайте любое число в промежутке от 20 от 100. Задумали? Сложите между собой составляющие его цифры. Вычтите получившуюся сумму из задуманного вами числа. И снова сложите цифры. Получилось 9? Если нет – перепроверьте свои вычисления. Здорово, правда? Вся математика построена на таких вот фокусах, о которых в школах нам почему-то не рассказывают. В этой книжке я покажу вам, как с помощью обычных чисел, фигур и простой логики творить настоящие чудеса. Добавим немного алгебры и геометрии, и перед нами откроются двери в производственные цеха фабрики магии, а может, и самого человеческого естества.
Эта книжка полна чисел, алгебры и математического анализа, геометрии и тригонометрии. Но есть в ней и много такого, что не столь хорошо знакомо неискушенному читателю и при этом не объяснено в мельчайших подробностях: треугольник Паскаля, математическая бесконечность, магические свойства некоторых чисел (9, π, e, i), последовательность Фибоначчи, золотое сечение… И хотя нескольких десятков страниц будет явно недостаточно, чтобы подробно рассказать о каждом из этих понятий, я все же надеюсь, что мне удастся объяснить вам их суть и показать, насколько удивительными и значительными они могут быть. И даже если вы с ними уже когда-то сталкивались, здесь вы увидите их под немного другим углом. Это расширит и обогатит ваши знания и представления, ведь чем глубже мы постигаем математику, тем более изощренной и восхитительной предстает перед нами ее магия. Вот, например, одна из самых любимых моих формул:
Магическая математика
Основано на реальных событиях.
Лёва усердно пытался решить задачи математического кружка, но задачи не поддавались. Пришлось просить помощи у отца.
— Ну, что вам тут задали? — спросил Олег Сергеевич. Он окончил мехмат МГУ и ему всё ещё казалось, что он с лёгкостью решит любую задачу. Уж за шестой-то класс точно!
— Вот, — Лёва протянул листок с условием, — тут три задачи. Учитель сказал, что это одна и та же задача, но я не понимаю, почему. Мне они кажутся абсолютно разными!
1. Имеется 9 слитков золота с маркировкой 100 г, 200 г, 300 г, 400 г, 500 г, 600 г, 700 г, 800 г, 900 г. Известно, что вес ровно одного слитка меньше заявленного. Как найти этот слиток на двухчашечных весах без гирь за два взвешивания?
2. Есть 9 борцов разной силы. В поединке любых двух всегда побеждает сильнейший. Можно ли разбить их на три команды по три борца так, чтобы во встречах команд по системе «каждый с каждым» первая команда по числу побед одержала верх над второй, вторая — над третьей, а третья — над первой?
3. В клетки таблицы 3 × 3 впишите различные натуральные числа так, чтобы произведения чисел в каждой строке, каждом столбце и на каждой из двух главных диагоналей были одинаковы.
— Хм, мне тоже так кажется. — Олег Сергеевич провёл рукой по некогда пышной шевелюре и задумался. — Если бы в третьей задаче речь шла не о произведениях, а о суммах, то её было бы легко решить. В математике это называется магическим квадратом. Магический квадрат 3 × 3, в котором записаны целые числа от 1 до 9, знали ещё в Древнем Китае более чем за 2000 лет до нашей эры! А ты сможешь заполнить клетки таблицы 3 × 3 числами от 1 до 9, чтобы суммы чисел в каждом столбце, каждой строке и на каждой из двух диагоналей были одинаковы?
— Папа, ты вместо того, чтобы помочь, задаёшь мне четвёртую задачу!? — возмутился Лёва.
— Подожди, возможно это необходимо. Давай решим её вместе! Какие у тебя идеи?
— Ну, чисел всего 9. Значит, можно попробовать перебрать варианты. — нерешительно произнёс Лёва.
— Не торопись. Смотри, в первую клетку таблицы можно записать целое число от 1 до 9, это 9 способов. В следующую выбираем уже из оставшихся, то есть 8-ю способами, и т. д. Получается, что всего способов 9 · 8 · 7 · 6 · 5 · 4 · 3 · 2 · 1. Мой смартфон показывает, что это число (математики его называют «9 факториал» и обозначают 9!) равно 362 880. Даже если проверять по таблице в секунду, на всю проверку уйдёт около 100 часов изнурительного однообразного труда. В общем, до следующего кружка не успеешь. Перебор можно подсократить за счёт одинаковых таблиц (отличающихся только поворотом или отражением), но это не тот путь, которым бы я советовал идти.
— Что же делать. — перебил Лёва.
— Думай! Знаем ли мы что-то про такую таблицу?
— Ну, знаем, что в ней все числа от 1 до 9, но не знаем, как они там переставлены. Ага, понял! Мы можем сказать, чему равна сумма чисел в строке или столбце. Так как общая сумма 1 + 2 + 3 +. + 9 равна 45, всего в таблице 3 столбца и в каждом сумма одинакова, то эта сумма должна равняться 45 : 3 = 15.
— Отлично! А можешь теперь сказать, какое число должно стоять в центре и почему?
Читатель, а ты сможешь ответить на этот вопрос?
— Ну, давай подумаем вместе, — Олег Сергеевич нарисовал на листе квадрат и 4 стрелки. — Просуммируем числа в таблице по четырём направлениям, показанным стрелками на рисунке 1. По условию, должно получиться 4 раза по 15, то есть в сумме 60. С другой стороны, в общую сумму войдут все числа таблицы по одному разу, кроме центрального числа (обозначим его через x), оно войдёт 4 раза вместо одного. Но сумму всех чисел в таблице мы уже знаем, она равна 45. Получаем, что 60 = 45 + 3x. Значит, x = 5. То есть в центре может стоять только 5.
— Здорово! Выходит, мы можем сильно сократить перебор? — спросил Лёва.
— Всё ещё проще. Поставим куда-нибудь девятку. Например, так (рис. 2).
Тогда вместо знака «?» стоит 1, ведь сумма чисел строки равна 15. Если в последнем столбце (там, где 1) не стоит 8, то сумма чисел в нём не больше 1 + 7 + 6 Рис. 4
Легко проверить, что такая таблица подходит.
— Но какая связь с нашими тремя задачами. Мы же просто решили задачу, которую нам не задавали! — казалось, что Лёва был расстроен.
Поэтому, заменив каждое число магического квадрата на двойку в степени, равной этому числу, мы получим искомую таблицу (рис. 5). Задача решена!
— Хорошо, но третья задача хотя бы тоже про таблицу. А как связать это с первой задачей?
— В ней же тоже есть набор из 9 чисел: от 100 до 900 с одинаковым шагом 100. Давай запишем их в виде магического квадрата с одинаковой суммой по строкам и столбцам, просто дописав нули к числам построенного магического квадрата (рис. 6).
Положим на первую чашку весов слитки, соответствующие числам первой строки, а на вторую — слитки, соответствующие числам второй строки (рис. 7). Если одна из чашек перевесила, то мы знаем набор из трёх слитков, в котором более лёгкий слиток. Если же весы в равновесии, то более лёгкий слиток в наборе последней строки. В любом случае, после первого взвешивания мы знаем строку таблицы, в наборе которой есть более лёгкий слиток.
Далее кладём на первую чашку весов слитки, соответствующие числам первого столбца, а на вторую чашку — слитки, соответствующие числам второго (рис. 8). Аналогично, находим столбец с наиболее лёгким слитком, и сам этот слиток — он на пересечении найденных строки и столбца!
— Красиво! А как быть с борцами? Там же вообще нет никаких чисел!
— Нет, значит их нужно ввести, — спокойно ответил Олег Сергеевич. Он только что понял, как нужно решать эту задачу. — Итак, у нас 9 борцов. Обозначим их силу числами от 1 до 9. Давай снова посмотрим на магический квадрат и отметим борцов, которые входят в наши команды (рис. 9).
Во встрече любых двух команд всего будет 9 поединков (можно образовать 3 × 3 = 9 разных пар соперников). Первая команда выиграет у второй со счётом 5 : 4, так как 2 > 1, 7 > 5, 7 > 1, 6 > 5, 6 > 1 (всего 5 побед из 9). Вторая команда выиграет у третьей со счётом 5 : 4, так как 9 > 4, 9 > 3, 9 > 8, 5 > 4, 5 > 3. И третья команда выиграет у первой со счётом 5 : 4, так как 4 > 2, 3 > 2, 8 > 2, 8 > 7, 8 > 6. Вот мы и разбили борцов на три команды как требовалось!
— Просто магия какая-то! — удивился Лёва.
— А математика это и есть магия, — загадочно улыбнулся Олег Сергеевич.
Глава 9 Искусство математической магии
Искусство математической магии
Я всегда получал удовольствие от игры с цифрами. Я нахожу арифметику такой же занимательной, как и магию. Но понимание магических секретов арифметики требует знаний алгебры. Конечно, есть и другие причины для ее изучения. Назову лишь несколько: сдача экзаменов, моделирование проблем из реального мира, программирование и возможность понимания высшей математики. Но интерес к алгебре у меня вызвало в первую очередь желание понять некоторые математические трюки. Их я вам сейчас и представлю!
Попросите добровольца в аудитории загадать любое число, состоящее из одной-двух цифр. Затем скажите, что никоим образом не можете знать, что это за число, и предложите сделать следующее.
3. Разделите сумму на 2.
4. Вычтите из нее исходное число.
Спросите: «Думаете ли вы сейчас о цифре 6?» Опробуйте этот трюк сначала на себе и увидите, что данная последовательность вычислений всегда в итоге приводит к цифре 6, какое бы число вы изначально ни выбрали.
Почему это работает
Этот трюк целиком основан на простой алгебре. Я иногда использую его как способ познакомить с алгеброй студентов.
Секретное число, выбранное добровольцем, можно обозначить как х. Тогда выполняемые действия представляем так:
1. 2х (удвоить число).
2. 2х + 12 (прибавить 12).
3. (2х + 12)/2 = х + 6 (разделить на 2).
4. х + 6 — х (вычесть исходное число).
Не важно, какое число выбрано, итоговый ответ всегда будет 6. При повторении данного приема попросите добровольца прибавить другое число на втором шаге (скажем, 18). Итоговый ответ будет половиной этого числа (а именно 9).
Следующий трюк существует уже не одно столетие. Сделайте так, чтобы человек из аудитории достал ручку и бумагу:
1) и тайно записал трехзначное число, цифры которого идут в порядке уменьшения (например, 851 или 973);
2) записал число в обратном порядке и вычел его из исходного числа;
3) к полученному ответу добавил его же, только в обратном порядке.
В конце последовательности магическим образом появится ответ 1089, какое бы число ни выбрал доброволец. Например:
Почему это работает
Независимо от того, какое трехзначное число вы или кто-либо другой выберете в этой игре, окончательный ответ всегда будет равен 1089. Почему? Обозначим аbс неизвестное трехзначное число. Алгебраически это эквивалентно:
100a + 10b + c.
Запись числа в обратном порядке (для вычитания из исходного) дает сbа, которое алгебраически равно:
100c + 10b + a.
После вычитания сbа из аbс выходит:
100a + 10b + c — (100c + 10b + a) = 100(a — c) + (c — a) = 99(a — c).
Поэтому после вычитания на шаге 2 должно получиться одно из следующих чисел, кратных 99: 297, 396, 495, 594, 693, 792 или 891. Каждое из них после прибавления к нему своей перевернутой версии в итоге даст 1089, что мы и видим на шаге 3.
ТРЮК С ПРОПУЩЕННОЙ ЦИФРОЙ
Используя число 1089 из предыдущего примера, вручите добровольцу калькулятор и попросите умножить 1089 на любое трехзначное число, не называя его. (Предположим, он тайно умножил 1089 х 256 = 278 784) Теперь поинтересуйтесь, сколько цифр в полученном ответе. Ответ — 6.
Затем попросите: «Громко назовите пять из этих шести цифр в любом порядке. Я попытаюсь определить недостающую». Предположим, доброволец громко перечисляет: «Два… четыре… семь… восемь… восемь». Вы вежливо говорите ему, что он пропустил цифру 7. Секрет основан на том, что число кратно 9 тогда, и только тогда, когда сумма составляющих его цифр кратна 9. Так как 1 + 0 + 8 + 9 = 18 кратно 9, значит, число 1089 кратно 9. Поэтому 1089 при умножении на любое целое число даст кратное 9. И раз уж прозвучавшие цифры в сумме дают 29, и следующее кратное 9, большее 29, это 36, то наш доброволец пропустил число 7 (так как 29 + 7 = 36).
Есть более утонченные способы заставить добровольца в конечном итоге прийти к кратному 9. Вот некоторые из моих любимых.
1. Пусть он наугад выберет шестизначное число, перемешает его цифры, затем отнимет меньшее из шестизначных чисел из большего. Поскольку мы производим вычитание двух чисел с одинаковой модульной суммой (в самом деле, сумма цифр идентична), полученная в итоге разность будет иметь нулевую модульную сумму, следовательно, число будет кратно 9. Далее продолжайте действовать, как было описано выше, чтобы найти недостающую цифру.
2. Пусть он тайно выберет любое четырехзначное число, запишет его в обратном порядке, а потом вычтет меньшее число из большего. (Получится кратное 9.) Затем пусть умножит результат на 3. Далее, как и раньше, вы ищете пропущенную цифру.
3. Попросите добровольца перемножать разные цифры до тех пор, пока их произведение не превратится в семизначное число. Это не гарантия получения числа, кратного 9, но на практике такую «гарантию» можно получить не меньше чем в 90 % случаев (с большой вероятностью перемножаемые цифры будут включать девятки или две тройки, или две шестерки, или 3 и 6). Я часто использую данный способ, выступая перед математически продвинутой публикой, которая может раскусить другие методы.
Однако существует одна проблема, за которой нужно постоянно следить. Предположим, прозвучавшие числа в сумме дают кратное 9 (скажем, 18). После такого ответа у вас не будет возможности определить, пропущен ли 0 или 9. Как справиться с этой ситуацией? Очень просто! Сжульничайте! Просто спросите: «Вы ведь не пропустили 0, не так ли?» Если 0 пропущен, то вы успешно провернули свой трюк. Если нет, скажите: «Ой, просто показалось, что вы отвлеклись! Вы не пропустили один, два, три или четыре, не так ли?» Доброволец либо покачает головой, либо скажет «нет». Затем вы продолжаете: «Как и не пропустили пять, шесть, семь или восемь. Вы не включили девять, не так ли?» Доброволец ответит утвердительно, а вы получите заслуженные аплодисменты!
Этот прием сочетает в себе быстрые вычисления в уме и поразительные предсказания. Вручите зрителю карту с расчерченными на ней десятью линиями, пронумерованными от 1 до 10.
Пусть он загадает два положительных числа от 1 до 20 и подпишет ими линии 1 и 2. Далее попросите его записать сумму 1-й и 2-й линий на линии 3. Затем сумму линии 2 и 3 на линии 4 и так далее, как проиллюстрировано ниже.
Пусть зритель покажет вам карту. Вы сразу же можете назвать ему сумму всех чисел на ней. Например, в нашем случае вы могли бы мгновенно объявить, что числа в сумме дают 671 (быстрее, чем зритель подсчитал бы это с калькулятором).
В качестве приза вручите зрителю калькулятор и попросите его разделить число на линии 10 на число с линии 9. В данном примере получится частное 257/159 = 1,616. Пусть он произнесет первые три цифры частного, а после перевернет карточку (там вы уже написали свое предсказание). Он будет очень удивлен увиденным 1,61!
Почему это работает
Для выполнения быстрого расчета нужно просто умножить число с линии 7 на 11. Здесь 61 х 11 = 671. Причина эффективности этого приема проиллюстрирована в таблице ниже. Если обозначить числа на линиях 1 и 2 как х и у соответственно, а затем просуммировать числа на всех линиях от 1 до 10, то в итоге выйдет 55х + 88у, что составляет 11 х (5х + 8у). А это равно произведению числа 11 на число на линии 7.
БЫСТРЫЕ КУБИЧЕСКИЕ КОРНИ
Попросите кого-нибудь выбрать двузначное число, но не называть его. Затем попросите возвести это число в куб, то есть умножить само на себя трижды, используя калькулятор. Например, если секретное число 68, пусть доброволец вычислит 68 х 68 х 68 = 314 432 и назовет ответ. Как только он произнесет его вслух, вы можете мгновенно раскрыть секрет исходного числа — это кубический корень 68. Как это делается?
Чтобы быстро вычислять кубические корни, нужно выучить кубы чисел от 1 до 10.
1 3 = 1
2 3 = 8
3 3 = 27
4 3 = 64
5 3 = 125
6 3 = 216
7 3 = 343
8 3 = 512
9 3 = 729
10 3 = 1000
Как только вы запомните эти значения, вычислять кубические корни станет так же легко, как и назвать значение числа ?. Приведем пример.
Чему равен кубический корень из 314 432?
Кажется, что это довольно сложное задание для начала, но не паникуйте, на самом деле оно довольно простое. Как обычно, будем двигаться постепенно.
1. Посмотрите на величину тысяч, 314 в данном примере.
2. Поскольку 314 лежит между 6 3 = 216 и 7 3 = 343, то кубический корень находится в диапазоне «60 плюс» (так как 60 3 = 216 000 и 70 3 = 343 000). Следовательно, первая цифра кубического корня будет 6.
3. Для определения последней цифры заметьте, что только куб числа 8 оканчивается на 2 (8 3 = 512), так что последней цифрой будет 8.
Поэтому кубический корень из 314 432 равен 68. Три простых шага — и вы у цели. Обратите внимание, что каждая цифра от 0 до 9 появляется по одному разу в виде последней цифры куба.
А теперь попрактикуйтесь.
Чему равен кубический корень из 19 683?
1. 19 находится между 8 и 27 (2 3 и 3 3 ).
2. Следовательно, кубический корень лежит в диапазоне «20 плюс».
Обратите внимание, что наши выводы по поводу последней цифры работают только тогда, когда исходное число является кубом целого числа. Например, кубический корень из 19 684 будет 27,0004572… Определенно не 27. Вот почему эта тема включена в раздел математической магии, а не в более ранние главы. (Кроме того, расчеты производятся настолько быстро, что кажется, будто без магии не обошлось!)
УПРОЩЕННЫЕ КВАДРАТНЫЕ КОРНИ
Квадратные корни так же просто вычислить, если задан полный квадрат. Например, если кто-то сказал вам, что квадрат двузначного числа равен 7569, то вы в состоянии мгновенно ответить, что исходное число (квадратный корень) равно 87. Вот как это делается.
1. Посмотрите на величину сотен (цифры, предшествующие последним двум) в данном примере.
2. Так как 75 находится между 8 2 (8 х 8 = 64) и 9 2 (9 х 9 = 81), то нам известно, что квадратный корень будет где-то в диапазоне «80 плюс». Следовательно, его первая цифра 8.
Существует два числа, квадраты которых заканчиваются на 9: 3 2 = 9, 7 2 = 49. Поэтому последняя цифра квадратного корня должна равняться 3 или 7. Таким образом, квадратный корень равен либо 83, либо 87. Какой из них?
3. Сравните исходное число с квадратом числа 85 (который можно легко посчитать как 80 х 90 + 25 = 7225). Так как 7569 больше, чем 7225, квадратный корень будет б?льшим числом, то есть 87.
Решим еще один пример.
Чему равен квадратный корень из 4761?
Поскольку 47 лежит между 6 2 = 36 и 7 2 = 49, ответ должен находиться в диапазоне «60 плюс». Если последняя цифра квадрата равна 1, то последняя цифра квадратного корня должна быть 1 или 9. Так как 4761 больше 65 2 = 4225, то квадратный корень должен равняться 69. Как и с предыдущим трюком для кубического корня, этот метод можно использовать только тогда, когда исходное число является полным квадратом.
Следующий трюк мне впервые показал Джеймс Рэнди, который эффективно использовал его в своей магии. В нем волшебник предсказывает сумму четырех случайно выбранных трехзначных чисел.
Чтобы подготовить такой фокус, понадобятся три колоды из девяти карт каждая и лист бумаги с записанным числом 2247, который вы запечатаете в конверт. Далее над каждым комплектом карт произведите следующие действия.
На колоде А запишите такие цифры (одно на каждую карту):
4286 5771 9083 6518 2396 6860 2909 5546 8174
На колоде Б запишите числа:
5792 6881 7547 3299 7187 6557 7097 5288 6548
На колоде В запишите следующие числа:
2708 5435 6812 7343 1286 5237 6470 8234 5129
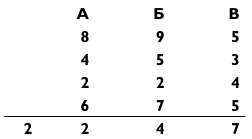
Выберите троих человек из аудитории и вручите им по колоде карт. Пусть каждый из них наугад вытащит оттуда одну карту. Допустим, это карты с числами 4286, 5792 и 5435. Теперь, соблюдая очередность, пусть каждый громко назовет одну из цифр четырехзначного числа: сначала человек А, потом человек Б и, наконец, человек В. Скажем, они назвали цифры 8, 9 и 5. Запишите их (получится число 895) и скажите: «Вы должны признать, что данное число — результат абсолютно случайного выбора и его нельзя заранее предсказать».
Далее пусть три человека назовут другие цифры своих карт. Скажем, 4, 5 и 3. Запишите 453 ниже числа 895. Затем повторите данную процедуру еще два раза для двух оставшихся чисел, получив в итоге четыре трехзначных числа, например:
Затем пусть кто-нибудь сложит эти четыре числа и назовет сумму. А дальше пусть кто-то откроет конверт и покажет ваше предсказание. Теперь наслаждайтесь аплодисментами!
Почему это работает
Взгляните на числа на картах каждой колоды и подумайте, прослеживается ли в них какая-либо последовательность. Каждый набор чисел в сумме дает одинаковую величину. Сумма цифр каждого числа колоды А равна 20. Сумма цифр каждого числа колоды Б — 23. И сумма цифр каждого числа колоды В равна 17. Поскольку цифры из колоды В, которые в правом столбике, всегда в сумме дают 17, то в итоговой сумме в разряде единиц можно записать 7 и запомнить перенос 1 в следующий разряд.
Так как цифры из колоды Б в сумме дают 23, то в итоговой сумме в разряде десятков можно записать 4 (3 + 1) и запомнить перенос 2 в следующий разряд. Наконец, цифры из колоды А в сумме дают 20, поэтому после прибавления 2 получим итоговую сумму 2247!
ДЕНЬ ДЛЯ ЛЮБОЙ ДАТЫ
Мы завершим нашу книгу одним из проверенных временем подвигов ментальных вычислений — определением дня недели, на который приходится чей-либо день рождения. Это действительно очень практический навык. Вряд ли вас каждый день кто-то будет просить возвести в квадрат трехзначное число, но почти ни один день не проходит без того, чтобы кто-то не упоминал дату из прошлого или будущего. Всего лишь немного практики, и вы сможете быстро и легко определять день недели практически любой исторической даты.
Сначала присвоим кодовый номер каждому дню недели.
Их легко запомнить.
Далее нам понадобится код для каждого месяца. Эти коды применимы для любого года за исключением високосных. Для високосного года (например, 2000, 2004, 2008 и т. д.) кодом для января будет 5, а для февраля — 1.
Теперь вычислим день недели для любой даты в 2006 году.
После этого опишем 2007 год, затем 2008-й и т. д., до конца вашей жизни. Когда все даты из будущего будут определены, мы заглянем в прошлое и вычислим дни недели для любой даты из 1900-х или любого другого века.
Каждому году присвоен кодовый номер, и в случае 2006 года таковым будет 0 (см. таблицу ниже).
Чтобы вычислить день недели, нужно просто сложить код месяца, день месяца (дата) и код года. Таким образом, для 3 декабря 2006 года рассчитываем
Код месяца + Дата + Код года = 4 + 3 + 0 = 7.
Следовательно, эта дата приходится на 7-й день недели, то есть воскресенье.
Что вы скажете о 18 ноября 2006 года? Поскольку код ноября — 2, имеем:
Код месяца + Дата + Код года = 2 + 18 + 0 = 20.
Что можно сказать о 2007 годе? Точнее, что происходит с вашим днем рождения при переходе от одного года к следующему? Большинство годов состоят из 365 дней, а так как 365 = 7 х 52 + 1, то день недели вашего рождения сдвинется на один день вперед. Если между вашими днями рождения 366 дней, то день недели вашего рождения сдвинется на два дня вперед. Поэтому для 2007 года мы вычисляем день недели как и раньше, но применяем код года, равный 1. Далее следует 2008 год — високосный. (Високосный год бывает раз в четыре года, так что 2000, 2004, 2008, 2012… 2096 — високосные годы XXI века.) Поэтому для 2008 года его код увеличивается на два и равен 3. Следующий 2009 год не високосный, поэтому код увеличивается на 1 (и равен 4).
Таким образом, для 2 мая 2007 года, например, имеем:
Код месяца + Дата + Код года = 0 + 2 + 1 = 3.
Следовательно, данная дата приходится на среду.
Для 9 сентября 2008 года имеем:
Код месяца + Дата + Код года = 4 + 9 + 3 = 16.
Отнимая наибольшее кратное 7, получаем 16–14 = 2, значит, эта дата приходится на вторник.
Но для 16 января 2008 года, поскольку этот год високосный, код месяца январь будет равен 5, а не 6. Поэтому:
Код месяца + Дата + Код года = 5 + 16 + 3 = 24,
и, следовательно, нужная дата попадает на день 24–21 = 3, который является средой.
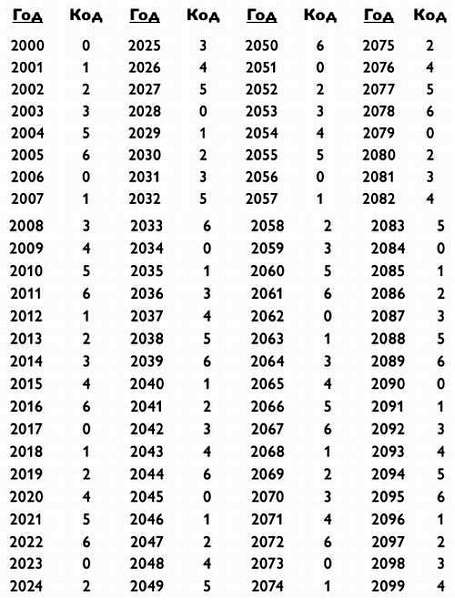
Мы перечислили все коды для каждого года XXI века в следующей таблице. Но вам не нужно запоминать ее. Можно устно посчитать код для любого года в промежутке от 2000 до 2099.
Для определения кода года 2000 + x берем частное х/4 (игнорируя остаток) и прибавляем его к х. Код года можно уменьшить путем вычитания из него кратного 7.
Например, для 2061 года имеем 61/4 = 15 (с остатком 1, который не учитывается). Тогда код 2061 года составит 61 + 15 = 76.
Или сокращенно 76–70 = 6.
Следовательно, для 19 марта 2061 получается:
Код месяца + Дата + Код года = 2 + 19 + 6 = 27.
Результат вычитания 27–21 = 6 говорит о том, что эта дата придется на субботу.
Что можно сказать о днях рождения между 1900 и 1999 годами? В этом случае задачу следует решать точно так же, как и предыдущие, но передвинуть итоговый ответ на один день вперед (или просто прибавить 1 к коду года). Тогда 19 марта 1961 года — это воскресенье.
Для даты 3 декабря 1998 года имеем 98/4 = 24 (с остатком 2, который не берем в расчет). Отсюда код 1998 года равен 98 + 24 + 1 = 123, где «плюс один» применяется ко всем номерам годов, больших 1900. Далее вычитаем наибольшее кратное 7.
Для удобства приведем числа, кратные 7, которые могут вам понадобиться:
7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126…
Так как 123–119 = 4, код 1998 года будет 4. Следовательно, для 3 декабря 1998 года имеем:
Код месяца + Дата + Код года = 5 + 16 + 3 = 24
и 11 — 7 = 4, так что эта дата приходится на четверг.
Для дат годов, больших 1800 и меньших 1900, нужно прибавлять 3 к коду соответствующего года из XXI века. Например, Чарльз Дарвин и Авраам Линкольн родились 12 февраля 1809 года. Так как код 2009 года — 4, то 1809-й будет иметь код 4 + 3 = 7, который можно сократить до нуля. Таким образом, для 12 февраля 1809 будет
Код месяца + Дата + Код года = 2 + 12 + 0 = 14
и 14–14 = 0, значит, оба родились в воскресенье.
Для дат 2100-х годов (то есть дат XXII столетия) следует прибавить 5 к коду соответствующего года XXI века (или вычесть из него 2, что эквивалентно). Например, код 2009 года равен 4, тогда 2109 год имеет код 4 + 5 = 9, который после вычитания 7 идентичен коду года 2.
Даты 1700-х годов (XVIII столетие) рассчитываются так же, как даты XXII века (путем прибавления 5 или вычитания 2), но здесь нужно быть внимательным. В то время был принят григорианский календарь, созданный в 1582 году. Но он не был официально принят англичанами (и американскими колониями) вплоть до 1752 года, когда среда 2 сентября вдруг стала четвергом 14 сентября. Удостоверимся, что 14 сентября 1752 года в самом деле было четвергом. Так как код 2052 года равен 2 (посмотрите в таблице выше или посчитайте 52 + 13–63 = 2), то 1752 год будет иметь код 0. Отсюда для 14 сентября 1752 года получаем:
Код месяца + Дата + Код года = 4 + 14 + 0 = 18
и 18–14 = 4, что действительно означает четверг. Однако наша формула не сработает для более ранних дат (которые исчислялись по юлианскому календарю)[18].
Наконец, отметим, что в соответствии с григорианским календарем високосный год наступает раз в четыре года, за исключением тех годов, которые делятся на 100, хотя есть и исключение из исключения: годы, делимые на 400, тоже являются високосными. Так, 1600, 2000, 2400 и 2800 годы будут високосными, а 1700, 1800, 1900, 2100, 2200, 2300 и 2500-й — нет. По сути, григорианский календарь повторяет себя каждые 400 лет, так что вы можете преобразовать любую дату из будущего в дату около 2000 года. Например, 19 марта 2361 года и 19 марта 2761 года придутся на тот же день недели, что и 19 марта 1961 года, которое мы ранее уже определили как воскресенье.
УПРАЖНЕНИЕ: ДЕНЬ ДЛЯ ЛЮБОЙ ДАТЫ
Определите день недели для следующих дат.
1. 19 января 2007 г.
2. 14 февраля 2012 г.
3. 20 июня 1993 г.
4. 1 сентября 1983 г.
5. 8 сентября 1954 г.
6. 19 ноября 1863 г.
7. 4 июля 1776 г.
8. 22 февраля 2222 г.
9. 31 июня 2468 г.
10. 1 января 2358 г.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
Глава 5 Искусство приближенной оценки
Глава 5 Искусство приближенной оценки До сих пор вы совершенствовали ментальные техники, необходимые для получения точных ответов в математических задачах. Однако часто бывает достаточно приблизительной оценки решения. Скажем, вы получаете расценки различных
Глава 7 Запоминающаяся глава для запоминания чисел[9]
Глава 7 Запоминающаяся глава для запоминания чисел[9] Наиболее часто мне задают вопрос о моей памяти. Нет, сразу скажу я вам, она у меня не феноменальная. Скорее, я применяю систему мнемотехники, которая может быть изучена любым человеком и описана на следующих страницах.
Глава 1
Глава 1 Кто Джон? Для того чтобы узнать, кого из двух братьев-близнецов зовут Джон, нужно спросить одного из них: «Джон говорит правду?». Если в ответ на этот вопрос последует «да», то независимо от того, лжет ли спрошенный близнец или говорит всегда только правду, он должен
Глава 2
Глава 2 1. История первая. По существу, Болванщик заявил, что варенье украли либо Мартовский Заяц, либо Соня. Если Болванщик солгал, то ни Мартовский Заяц, ни Соня не украли варенье. Но тогда Мартовский Заяц, поскольку он не украл варенье, дал правдивые показания.
Глава 3
Глава 3 14. Гусеница и Ящерка Билль. Гусеница считает, что и она, и Ящерка Билль не в своем уме. Если бы Гусеница была в здравом уме, то мнение о том, что и она, и Ящерка Билль не в своем уме, было бы ложно. Следовательно, Гусеница (будучи в здравом уме) не могла бы придерживаться
Глава 4
Глава 4 26. Сколько кренделей у каждого? Назовем одной порцией все крендельки, которые достались Соне, сколько бы их ни было. Тогда Соне досталась 1 порция. Мартовскому Зайцу досталось вдвое больше крендельков, чем Соне (потому что Соню Болванщик посадил на такое место, где
Глава 5
Глава 5 42. Появление первого шпиона. С заведомо не может быть рыцарем, так как ни один рыцарь не стал бы лгать и утверждать, будто он шпион. Следовательно, С либо лжец, либо шпион. Предположим, что С шпион. Тогда показание А ложно, значит, А шпион (А не может быть шпионом, так
Глава 6
Глава 6 52. Первый вопрос. Алиса ошиблась, записав одиннадцать тысяч одиннадцать сотен и одиннадцать как 11111, что неверно! Число 11111 – это одиннадцать тысяч одна сотня и одиннадцать! Для того чтобы понять, как правильно записать делимое, сложим одиннадцать тысяч,
Глава 7
Глава 7 64. Первый раунд (Красное н черное). Если внезапно заговоривший братец сказал правду, то его звали бы Траляля и в кармане у него была бы черная карта. Но тот, у кого в кармане карта черной масти, не может говорить правду. Следовательно, он лжет. Значит, в кармане у него
Глава 9
Глава 9 Во всех решениях этой главы А означает первого подсудимого, В – второго и С – третьего.78. Кто виновен? Из условий задачи известно, что виновный дал ложные показания. Если бы В был виновен, то он сказал бы правду, когда признал виновным себя. Следовательно, В не может
Глава 11
Глава 11 88. Всего лишь один вопрос. Действительно следуют. Рассмотрим сначала утверждение 1. Предположим, некто убежден, что он бодрствует. В действительности он либо бодрствует, либо не бодрствует. Предположим, что он бодрствует. Тогда его убеждение правильно, но всякий,
Глава 1
Глава 1 graphics46 Кто Джон?Чтобы узнать, кто из двух братьев Джон, спросите одного из них: «Джон правдив?» Если он ответит «да», это должен быть Джон, независимо от того, солгал он или сказал правду. Если же он ответит «нет», значит, он не Джон. И вот как это подтверждается.Ответив
Глава 7
Глава 7 graphics54 64. Первый раундЕсли бы братец говорил правду, его звали бы Траляля и у него была бы карта черной масти. Но он не может говорить правду, если у него в кармане карта черной масти. Поэтому он лжет. Это означает, что у него действительно карта черной масти, а