в чем измеряются касательные напряжения
Касательное механическое напряжение
Касательное механическое напряжение
| Механика сплошных сред | ||||||||||
 | ||||||||||
Сплошная среда
|
Механическое напряжение — это мера внутренних сил, возникающих в деформируемом теле под влиянием внешних воздействий. Механическое напряжение в точке тела измеряется отношением упругой силы, возникающей в теле при деформации, к площади малого элемента сечения, перпендикулярного к этой силе.
Различают две составляющие вектора механического напряжения:
В системе СИ механическое напряжение измеряется в паскалях.
Полезное
Смотреть что такое «Касательное механическое напряжение» в других словарях:
Механическое напряжение — У этого термина существуют и другие значения, см. Напряжение. Механическое напряжение Размерность L−1MT−2 Единицы измерения СИ … Википедия
Нормальное механическое напряжение — Механика сплошных сред Сплошная среда Классическая механика Закон сохранения массы · Закон сохранения импульса … Википедия
Напряжение (механическое) — Механика сплошных сред Сплошная среда Классическая механика Закон сохранения массы · Закон сохранения импульса … Википедия
Напряжение — Напряжение: В Викисловаре есть статья «напряжение» Электрическое напряжение между точками A и B отношение работы электрического поля при переносе пробного заряда из точки A в B к величине этого пробного заряда. Номинальное напряжение… … Википедия
Напряжение — [stress] 1. Мера внутренних сил, возникающих в образце (изделии) под влиянием внешних воздействий, равная отношению величины равнодействвующей силы к площади ее приложения (механическое напряжение); размерность МПа: Смотри также: электрическое… … Энциклопедический словарь по металлургии
Напряжение — механическое, мера внутренних сил, возникающих в деформируемом теле под влиянием внешних воздействий. При изучении Н. в любой точке проводят сечение тела через эту точку (рис. 1). Взаимодействие соприкасающихся по сечению частей тела… … Большая советская энциклопедия
Арка — У этого термина существуют и другие значения, см. Арка (значения). Арка из каменной кладки 1. Замковый камень 2. Клинчатый камень 3. Внешн … Википедия
Гука закон — основной закон, выражающий связь между напряжённым состоянием и деформацией упругого тела. Установлен англ. физиком Р. Гуком в 1660 для простейшего случая растяжения или сжатия стержня в форме: абсолютное удлинение (укорочение) Δl… … Большая советская энциклопедия
Нормальные и касательные напряжения.
Единицы нормальных и касательных напряжений в СИ – паскаль (Па). Один паскаль – это напряжение, при котором на площадке в один квадратный метр возникает внутренняя сила, равная одному ньютону. Часто используют значения: 1 МПа = 10 6 Па. В технической системе единицы напряжения измеряются в килограммах силы на миллиметр в квадрате (кгс/мм 2 ).
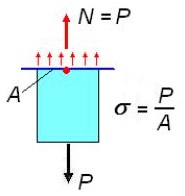
Напряжения при растяжении и сжатии.В поперечных сечениях при растяжении-сжатииимеют место только нормальные напряжения σ, которые определяются отношением внутренней силы N к площади A соответствующего поперечного сечения стержня.
Напряжения в поперечном сечении при растяжении.
Знак напряжений зависит от знака внутренней силы на рассматриваемом участке стержня. Для обеспечения необходимой прочности элементов и конструкций напряжения не должны превышать допустимых значений. При растяжении и сжатии в сечении действует только нормальное напряжение. Напряжения могут рассматриваться как силы, приходящиеся на единицу площади.
Таким образом, направление и знак напряжения в сечении совпадают с направлением и знаком силы в сечении.
Нормальное напряжение можно рассчитать по формуле:
Таким образом: величина напряжения прямо пропорциональна продольной силе и обратно пропорциональна площади поперечного сечения.
Нормальные напряжения действуют при растяжении от сечения, а при сжатии к сечению.
Размерность напряжений: Н/м 2 (Па), однако это слишком малая единица, и практически напряжения рассчитывают в Н/мм 2 (МПа):
Поперечные размеры стержня в результате деформирования также изменяются, при этом при растяжении они уменьшаются, а при сжатии – увеличиваются.
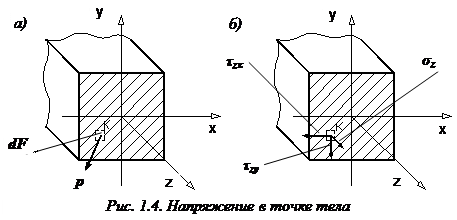
Напряжение в точке тела
Напряженное состояние в точке тела является ключевым понятием в сопромате. Необходимость введения понятия напряжения в точке для суждения об интенсивности внутренних сил в некоторой точке сечения стержня вызвана неравномерным распределением внутренних сил по длине и поперечному сечению в общем случае нагружения.
Напряжение в точке тела K (обозначено буквой p) – это интенсивность внутренней силы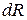 
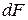
, возникающей на бесконечно малой площадке 
в окрестности данной точки (рис. 1.4, а).
В количественном выражении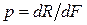 
.
Понятие о напряжении в точке твердого тела в некотором смысле напоминает понятие о давлении, действующем, например, внутри жидкости. Однако давление в точке жидкости одинаково во всех направлениях. Если проведем через точку K тела другое сечение, иной будет внутренняя сила. Следовательно, иным будет и напряжение, хотя оно возникает в той же самой точке K.
Напряжение в точке тела в разных направлениях (на разных площадках, проходящих через данную точку тела) может быть различным (в частности, оно может возникать только в одном направлении).
Понятие о напряжении в точке деформируемого твердого тела ввел в 1822 г. французский ученый Огюстен Луи Коши.
Основную роль в расчетах прочности играет не полное напряжение p, а его проекции на оси координат x, y и z: нормальное напряжение (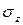 
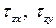
– сигма), направленное по перпендикуляру к площадке (параллельно оси z), и касательные напряжения ( 
– тау), лежащие в плоскости сечения и направленные, соответственно, вдоль осей x и y (рис. 1.4, б). Первый индекс у касательных напряжений характеризует нормаль к площадке z, на которой они возникают.
Между полным (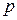
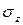
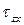
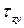
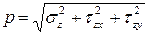
), нормальным () и касательными напряжениями ( 
и 
) существует зависимость:
.
Касательные напряжения служат мерой тенденции одной части сечения смещаться (или скользить) относительно другой его части.
Единицы нормальных и касательных напряжений в СИ – паскаль (Па). Один паскаль – это напряжение, при котором на площадке в один квадратный метр возникает внутренняя сила, равная одному ньютону (то есть равная, приблизительно, весу одного яблока). Как мы увидим в дальнейшем, эта единица напряжения мизерно мала. В сопромате чаще используются другие единицы:
1 МПа = 106 Па; 1 кН/см2 = 107 Па.
В чем измеряются касательные напряжения
Во время работы на элементы конструкции действуют внешние усилия, создающие напряжения и деформации. Рассмотрим общие методы анализа напряженного состояния.
3. Нормальные и касательные напряжения
Метод сечений. Пусть на элемент конструкции, условно изображенный на рис. 2.1, а, действуют внешние силы (сосредоточенные или распределенные на участках поверхности). Считаем, что элемент конструкции под действием указанных сил находится в равновесии. Проведем плоскость П, которая рассечет элемент на две части, и рассмотрим одну из частей, например левую (рис. 2.1, б).
Рис. 2.1. Напряжения в сечении элемента
Приложим к поверхности сечения П силы взаимодействия между обеими частями элемента. Когда тело находится в равновесии, то и любая часть тела также будет в равновесии, если к поверхности сечения приложить силы взаимодействия между частями. Силы, действующие в сечений, представляют собой силы взаимодействия между частицами материала, вызванные внешней нагрузкой на. элемент. Из условия равновесия рассматриваемой части тела можно определить главный вектор и главный момент внутренних сил, действующих по сечению П. В этом состоит сущность метода сечений — одного из ражных методов механики деформируемых сред. Распределение внутренних усилий по сечению заранее неизвестно и составляет одну из главных задач дальнейшего изучения.
Понятие напряжения.
Оказывается необходимым ввести характеристику интенсивности сил взаимодействия — напряжения, которые в разных точках сечения могут быть, разумеется, различныки.
Пусть на малую площадку 
расположенную в окрестности точки А (рис. 2.1, б), действует сила 
.
Назовем напряжением 
в точке А рассматриваемого сечения предел отношения
при условии, что 
стремится к нулю.
Вектор напряжения совпадает по направлению с вектором усилия 
. Отметим, что напряжения в сечении элемента не могут быть определены только из уравнений статики (уравнений равновесия). Для их нахождения, как будет ясно из дальнейшего, необходимо разобраться в характере деформаций элемента. Однако в ряде случаев можно сделать некоторые обоснованные предположения о распределении напряжений, что позволит найти их величину и без рассмотрения деформаций. Использование предположений (гипотез), основанных на результатах экспериментальных исследований и дающих достаточную точность при решении инженерных задач, составляет примечательную черту прикладных технических дисциплин, в частности сопротивления материалов.
Рис. 2.2. Напряжения растяжения в сечении болта
При растяжении болта, усилием 
(рис. 2.2) есть все основания предположить, что напряжения в сечении П (поперечное сечение стержня болта) направлены нормально к плоскости сечения и распределены равномерно. Тогда значение растягивающего напряжения
Из последнего равенства очевидно, что напряжение имеет размерность 
Размерность обозначается символом 
(начальные буквы слова «dimension» — размерность).
В международной системе единиц СИ для измерения напряжен 
(давления) применяется специальная единица — паскаль: 
. Это — очень маленькая величина, и практические расчеты ведут, измеряя напряжения в мегапаскалях 
причем
В технической литературе напряжения часто измеряют в системе МКС.
Связь единиц измерения такова: 1 МПа = 0,1 кгс/мм2. В общем случае напряжения в разных точках сечения могут быть различными.
Еще одно важное обстоятельство состоит в том, что напряжение в точке зависит также и от положения плоскости сечения. Поэтому надо всегда указывать не только точку тела, где определяется напряжение, но и ориентацию сечения (площадки), проходящего через рассматриваемую точку.
Нормальные и касательные напряжения.
Микроосновы дисциплины
«Сопротивление материалов».
Устойчивость стержня.
Основные требования к деталям и конструкциям. Детали должны быть: прочными, то есть не разрушаться под нагрузкой, жесткими, то есть не деформироваться под нагрузкой, устойчивыми, то есть не терять первоначальную форму упругого равновесия.
Виды расчетов в сопротивлении материалов. Расчет на прочность обеспечивает неразрушение конструкции. Расчет на жесткость обеспечивает деформации конструкции под нагрузкой в пределах допустимых норм. Расчет на устойчивость обеспечивает сохранение необходимой формы равновесия и предотвращает внезапное искривление длинных стержней.
Формы элементов конструкции:
а,б,в – брус, г – оболочка, д – пластина, е – массивное тело
Классификация нагрузок. Различают внешние и внутренние силы и моменты.
Схематизация внешних сил.
Виды деформаций:
а – сжатие, б – растяжение, в – изгиб, г – сдвиг (срез), д – кручение
В зависимости от характера внешних сил различают следующие виды деформаций:
изгиб – состоит в искривлении оси.
Бывают более сложные деформации, которые образуются сочетанием нескольких основных видов деформаций, например – изгиб и кручение.
Внутренние силы.
Нормальные и касательные напряжения.
Единицы нормальных и касательных напряжений в СИ – паскаль (Па). Один паскаль – это напряжение, при котором на площадке в один квадратный метр возникает внутренняя сила, равная одному ньютону. Часто используют значения: 1 МПа = 10 6 Па. В технической системе единицы напряжения измеряются в килограммах силы на миллиметр в квадрате (кгс/мм 2 ).
Напряжения при растяжении и сжатии. В поперечных сечениях при растяжении-сжатииимеют место только нормальные напряжения σ, которые определяются отношением внутренней силы N к площади A соответствующего поперечного сечения стержня.
Дата добавления: 2019-08-30 ; просмотров: 3086 ; Мы поможем в написании вашей работы!