в чем измеряют магнитную индукцию

Измерение магнитной индукции и напряженности магнитного поля

Наиболее распространенными магнитоизмерительными приборами для определения индукции и напряженности являются: Тм с преобразователем Холла, ферромодуляционный и ядерно-резонансный тесламетр.

Тм с преобразователем Холла определяют параметры средних (от 10-5 до 10-1 Тл) и сильных (10-1 до102 Тл) МП. Принцип работы таких тесламетров основан на появлении ЭДС в полупроводниках, помещенных в зону влияния МП.

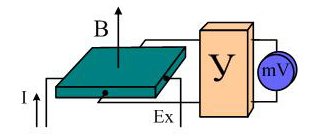
При этом вектор магнитной индукции искомого МП должен быть перпендикулярен пластине полупроводника.

Через тело полупроводника протекает электрический ток I. В результате на боковых гранях пластины образуется разность потенциалов, которую называют ЭДС Холла. ЭДС определяется компенсационным методом или милливольтметром, шкала которого градуирована в теслах. На практике ЭДС Холла зависит от следующих параметров:

где С – коэффициент, учитывающий конструктивные параметры пластины полупроводника; I – сила тока, А; В – магнитная индукция, Тл.

Зная силу тока I, коэффициент С и значение Ех, прибор градуируют в единицах измерения МП, при условии, что сила тока постоянна.

Тм с преобразователем Холла просты в применении, имеют небольшие размеры, что позволяет применять их при измерениях в малых зазорах. С их помощью определяют параметры постоянных, переменных и импульсных полей.

Пределы измерения обычного прибора от 2*10-3 до 2 Тл, с относительной погрешностью ±1,5–2,5%.

Вторым видом приборов для определения характеристик МП является ферромодуляционный тесламетр (ФМТ). Используют ФМТ для измерения слабых и средних, постоянных и переменных (до 1кГц) МП.

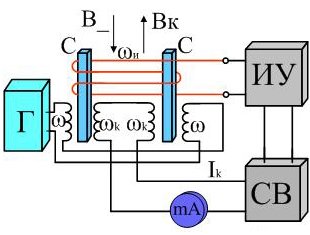
В основу работы ФМТ заложено свойство пермаллоевых сердечников С, изменять свое магнитное состояние, при одновременном воздействии на них постоянного и переменного МП.

Наиболее широкое применение в схеме измерения рис.2 нашли дифференциальные ферромодуляционные преобразователи. Генератор Г служит для создания переменного МП, которое посредствам катушек ω влияет на сердечники С.

В связи с тем, что эти катушки включены встречно, т. е. конец одной совпадает с другой, ЭДС в цепи индикаторной катушки ωи отсутствует.

Если внести сердечники С в постоянное МП (измеряемое поле), так чтобы вектор магнитной индукции был параллелен оси сердечников, в измерительной обмотке появится ЭДС. Это явление происходит благодаря физическим свойствам пермаллоя, изменять свое магнитное состояние под воздействием двух разнородных полей.

Синхронный выпрямитель получает с выхода ИУ усиленный сигнал ЭДС второй гармоники, преобразует ЭДС в пропорциональный ей (а значит и Н и В_) ток компенсации Iк.

Ток компенсации, протекая по компенсирующим обмоткам ωк, создает компенсирующее поле Вк, которое стремится уравновеситься с В_, и имеет встречное направление. Миллиамперметр, по которому также протекает ток Iк, градуирован в теслах.

Ферромодуляционные тесламетры имеют высокую чувствительность, точность, и могут быть использованы для непрерывных измерений параметров магнитного поля. Пределы измерения ФМТ от 10-6 до 1 мТл, с погрешностью от 1 до 5%.

Тесламетры с квантовыми магнитоизмерительными преобразователями используют для измерения средних и слабых МП, постоянных и переменных частотой до 20 кГц полей. Принцип действия квантовых магнитоизмерительных преобразователей заключается во взаимодействии ядер молекул вещества с МП.

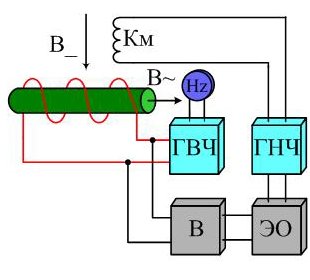
На рис.3 представлена схема распространенного ядерно-резонансного преобразователя. В колбе находится рабочее вещество. По средствам генератора высокой частоты ГВЧ и катушки, охватывающей витками колбу, к рабочему веществу приложено переменное МП.

Взаимодействие ядер с МП называется прецессией. Итак, в колбе частицы прецессируют вокруг вектора магнитной индукции переменного поля.

Под прямым углом, на колбу с рабочим веществом, начинает действовать измеряемое постоянное МП В_. Плавно изменяя частоту переменного поля, добиваются ядерного магнитного резонанса – совпадения частоты прецессии с частотой переменного поля. Резонанс заключается в увеличении амплитуды прецессии.

Этот процесс сопровождается поглощением части энергии переменного ВЧ поля, что приводит к изменению добротности катушки, а соответственно и изменению напряжения на ее концах.

Явление резонанса можно наблюдать на экране электронного осциллографа ЭО, на горизонтальный вход которого подается напряжение ГНЧ, а на вертикальный – выпрямленное напряжение рабочей катушки. ГНЧ питает током низкой частоты катушку модуляции Км, которая служит для модуляции магнитной индукции В_.

Ядерно-резонансные тесламетры являются самыми точными, их относительная погрешность составляет 0,001–0,1%, в области значений 10-2–10 Тл.

Источник

Принципиальные методы измерения напряженности и индукции магнитного поля в магнетиках

Прямое измерение индукции магнитного поля

Прямое измерение индукции магнитного поля при помощи витка с током основано на явлении электромагнитной индукции Фарадея.

Напомним один из основных законов электромагнетизма.

Закон электромагнитной индукции Фарадея

При изменении магнитного потока, проходящего через замкнутый контур, в контуре возникает ЭДС индукции.

Скорость изменения магнитного потока через замкнутый контур по модулю равна ЭДС индукции, возникающей в контуре.

Косвенные методы измерение напряженности и индукции магнитного поля

Прямое (непосредственное) измерение величины B описанным выше способом возможно не всегда. Например, так невозможно измерить индукцию магнитного поля в веществе.

Необходимо принимать во внимание, что при переходе границы магнетика нормальные составляющие вектора магнитной индукции и тангенциальные составляющие вектора напряженности непрерывны.

Как измеряют вектор магнитной индукции в веществе? Для этого в исследуемом материале делают полость и проводят измерение. Также при обработке результатов учитывают форму полости.

Способ 2. В магнетике создают бесконечно узкую щель. Удаление вещества, учитывая бесконечно малый размер щели, не сказывается на магнитном поле (удалением вещества можно пренебречь). Измеряя индукцию в щели, узнаем индукцию магнитного поля в веществе.

Магнитная индукция в зазоре и сердечнике одинакова по модулю, если зазор бесконечно мал.

H F e l F e + H v l v = N I

Подставим сюда записанные выше выражение для напряженности:

Отсюда выразим магнитную индукцию:

Магнитная проницаемость железа велика, и соотношением l F e μ F e ≪ 1 можно пренебречь. Тогда выражение для индукции запишется в виде:

Измерение напряженности магнитного поля методом Гаусса

Данный метод применяется для измерения магнитного поля Земли.

Под воздействием полей B → и B → 1 стрелка установится под углом α к постоянному магнитному полю:

Источник

Средства и методы измерения магнитных величин

Иногда в процессе работы, научного исследования или простого любопытства возникает необходимость в определении магнитных величин. Их можно либо рассчитать по формулам, имея необходимые данные, или же произвести замер магнитной величины. В данной статью мы будем рассматривать измерение магнитных величин.

К магнитным величинам, как правило, относят напряженность магнитного поля H, поток магнитный Ф, а также величину магнитной индукции В.

Методику измерения магнитных величин основывают на преобразовании этих величин в электрические, и с помощью электроизмерительного прибора приводят к доступному для человеческого восприятия виду.

Наиболее широкое распространение получили два метода измерения – индукционный и гальваномагнитных эффектов. Разберем каждый в отдельности.

Индукционный метод

Он основан на эффекте возникновения ЭДС в витках электромагнитной катушки при изменении магнитного потока Ф, который сцепляется с ним, как это показано ниже:

Аналитическая зависимость будет иметь вид:

Где: w – число витков в катушке, ψ – потокосцепление.

Если магнитный поле будет однородно, то поток магнитный Ф будет связан с магнитной индукцией В следующим выражением – Ф = Вs, где s – представляет собой площадь сечения катушки.

Если среда, в которой происходит такое явление воздушная, то индукция магнитная В будет связана с напряженностью магнитного поля H такой зависимостью: В = μ₀Н, где μ₀ – магнитная постоянная для воздушной среды.

Можно сделать вывод, что индукционный метод позволяет определить напряженность магнитного поля, магнитный поток и индукцию магнитную:

Приборы, которые измеряют магнитный поток, называют веберметрами.

Простейшая схема такого устройства показана ниже:

Она состоит из индукционной катушки, обозначенной на схеме (W_к) и интегрирующего устройства ИУ. Магнитоэлектрические гальванометры, без устройств противодействующего момента, зачастую используют в качестве интегрирующих устройств ИУ. Если катушку измерительного устройства подносить или удалять от магнитного поля, то отклонения измерительного механизма будет пропорционально магнитному потоку и определятся зависимостью:

Где: α – угол отклонения стрелки прибора, W_к – количество витков в катушке измерительной, С_ф – цена деления веберметра.

Метод гальваномагнитных эффектов

Очень широкое применение из этих гальваномагнитных эффектов получил так называемый метод Холла.

Суть его заключается в следующем – если через пластину, которая состоит из полупроводника и находится в магнитном поле с индукцией В, пропустить какой – то ток I, то между точками Х – Х возникнет разность потенциалов Е_х, которая носит название ЭДС Холла. Схема приведена ниже:

ЭДС Холла будет равна:

Где: S_п – чувствительность преобразователя при токе I.

Устройства, которые измеряют магнитную индукцию В называют тесламетрами.

Упрощенная схема такого прибора с преобразователем Холла (ПХ) показана ниже:

По такой схеме работает тесламетр типа Ш1-8, который может измерять индукцию в диапазоне от 0,01 – 1,6 Тл. Основная погрешность этого устройства не превышает ±2%.

Также датчики Холла очень активно применяют в современных асинхронных электродвигателях с векторным управлением по потокосцеплению электрической машины.

Источник

Магнитная индукция, магнитный поток: определение, формулы, смысл

Физический смысл магнитной индукции

Физически это явление объясняется следующим образом. Металл имеет кристаллическую структуру (катушка состоит из металла). В кристаллической решетке металла расположены электрические заряды — электроны. Если на металл не оказывать ни какое магнитное воздействие, то заряды (электроны) находятся в покое и никуда не движутся.

Васильев Дмитрий ПетровичПрофессор электротехники СПбГПУ Если же металл попадает под действие переменного магнитного поля (из-за перемещения постоянного магнита внутри катушки – именно перемещения), то заряды начинают двигаться под действием этого магнитного поля.

В результате чего в металле возникает электрический ток. Сила этого тока зависит от физических свойств магнита и катушки и скорости перемещения одного относительно другого.

При помещении металлической катушки в магнитное поле заряженные частицы металлический решетки (в кашутке) поворачиваются на определенный угол и размещаются вдоль силовых линий магнитного поля.

Чем выше сила магнитного поля, тем больше количество частиц поворачиваются и тем более однородным будет являться их расположение.

Магнитные поля, ориентированные в одном направлении не нейтрализуют друг друга, а складываются, формируя единое поле.

Формула магнитной индукции

где, В — вектор магнитной индукции, F — максимальная сила действующая на проводник с током, I — сила тока в проводнике, l — длина проводника.

Формула магнитной индукции:

Формула магнитной индукции: B = Mmax/IS

Другие формулы, где встречается B

Эти формулы также можно использовать для её расчёта.

Сила Ампера:

Сила Ампера: Fa=IBL sinα

Сила Лоренца:

Сила Лоренца: Fл = qvB sinα

Магнитный поток:

Магнитный поток: Ф = BS cosα

Магнитный поток

Магнитный поток это скалярная величина, которая характеризует действие магнитной индукции на некий металлический контур.

Магнитная индукция определяется числом силовых линий, проходящих через 1 см2 сечения металла.

Магнитометры, используемые для ее измерения, называют теслометрами.

Абрамян Евгений ПавловичДоцент кафедры электротехники СПбГПУ Единицей измерения магнитной индукции в системе СИ является Тесла (Тл).

После прекращения движение электронов в катушке сердечник, если он выполнен из мягкого железа, теряет магнитные качества. Если он изготовлен из стали, то он имеет способность некоторое время сохранять свои магнитные свойства.

Взаимодействие магнитов

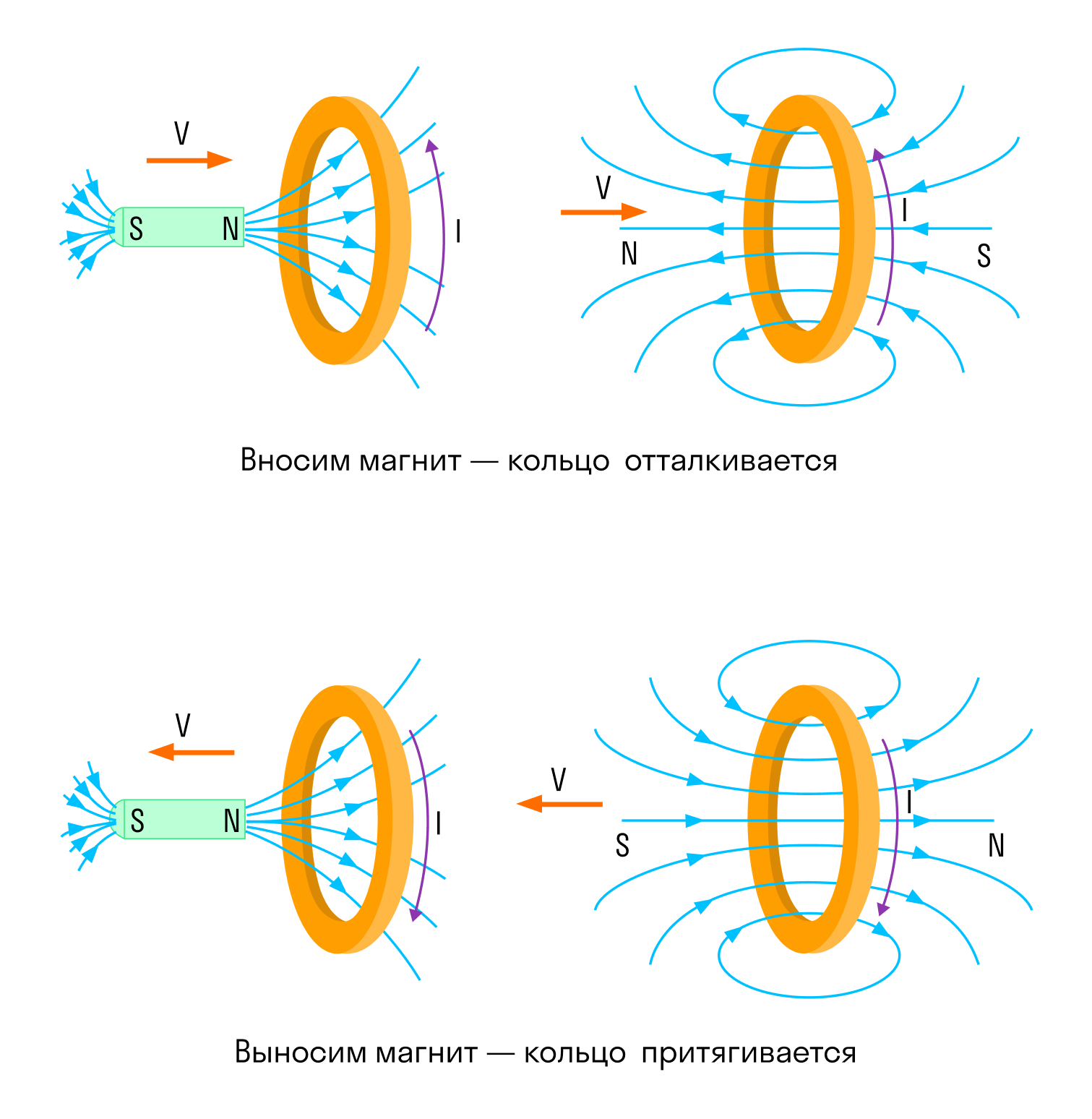
Постоянный магнит (или магнитная стрелка) ориентируется вдоль магнитного меридиана Земли. Тот его конец, который указывает на север, называется северным полюсом (N), а противоположный конец — южным полюсом (S). Приближая два магнита друг к другу, заметим, что одноименные их полюсы отталкиваются, а разноименные — притягиваются (рис. 1).

Если разделить полюса, разрезав постоянный магнит на две части, то мы обнаружим, что каждая из них тоже будет иметь два полюса, т. е. будет постоянным магнитом (рис. 2). Оба полюса — северный и южный, — неотделимые друг от друга, равноправны.

Магнитное поле, создаваемое Землей или постоянными магнитами, изображается, подобно электрическому полю, магнитными силовыми линиями. Картину силовых линий магнитного поля какого-либо магнита можно получить, помещая над ним лист бумаги, на котором насыпаны равномерным слоем железные опилки. Попадая в магнитное поле, опилки намагничиваются — у каждой из них появляется северный и южный полюсы. Противоположные полюсы стремятся сблизиться друг с другом, но этому мешает трение опилок о бумагу. Если постучать по бумаге пальцем, трение уменьшится и опилки притянутся друг к другу, образуя цепочки, изображающие линии магнитного поля.

На рис. 3 показано расположение в поле прямого магнита опилок и маленьких магнитных стрелок, указывающих направление линий магнитного поля. За это направление принято направление северного полюса магнитной стрелки.

Направление вектора МИ

Направление магнитных полей может указать стрелка магнита, помещаемая в эти поля. Она будет крутиться до тех пор, пока не остановится. Северный конец стрелки покажет, куда ориентирован B→ орт того или иного поля.

Линии магнитной индукции

Таким же образом ведёт себя рамка с током, имеющая возможность без помех ориентироваться в МП. Направленность вектора индукции указывает ориентацию нормали к такому замкнутому электромагнитному контуру.

Внимание! Здесь используют правило буравчика (правого винта). Если винт вращать так, как направлен ток в рамке, то поступательное продвижение винта совпадёт с направлением положительной нормали.

В некоторых случаях, чтобы найти направление, применяют правило правой руки.

Наглядное отображение линий МИ

Линию, к которой можно провести касательную, совпадающую с B→, называют линией магнитной индукции (МИ). С помощью таких линий можно визуально отобразить магнитное поле. Это сомкнутые контурные чёрточки, которые охватывают токи. Их густота всегда пропорциональна величине B→ в конкретной точке МП.

Информация. Когда имеют дело с МП прямого движения заряженных частиц, то эти линии изображаются в виде концентрических окружностей. Они имеют свой центр, расположенный на прямой линии с током, и находятся в плоскостях, расположенных под прямым углом к нему.

С направлением магнитных линий также можно определиться, пользуясь правилом буравчика.

Основные формулы для вычисления вектора МИ

Вектор магнитной индукции, формула которого B = Fm/I*∆L, можно находить, применяя другие математические вычисления.

Закон электромагнитной индукции

Закон электромагнитной индукции (закон Фарадея) звучит так:

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.

Математически его можно описать формулой:

Ɛi — ЭДС индукции [В]

ΔФ/Δt — скорость изменения магнитного потока [Вб/с]

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из ​N витков (то есть он — катушка), то ЭДС индукции будет вычисляться следующим образом.

Закон Фарадея для контура из N витков

Ɛi — ЭДС индукции [В]

ΔФ/Δt — скорость изменения магнитного потока [Вб/с]

N — количество витков [-]

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ​R​:

Закон Ома для проводящего контура

Ɛi — ЭДС индукции [В]

I — сила индукционного тока [А]

R — сопротивление контура [Ом]

Если проводник длиной l будет двигаться со скоростью ​v​ в постоянном однородном магнитном поле с индукцией ​B​ ЭДС электромагнитной индукции равна:

ЭДС индукции для движущегося проводника

Ɛi — ЭДС индукции [В]

B — магнитная индукция [Тл]

v — скорость проводника [м/с]

l — длина проводника [м]

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

Закон Био-Савара-Лапласа

Формула ЭДС индукции

Описывает правила нахождения B→ магнитного поля, которое создаёт постоянный электроток. Это экспериментально установленная закономерность. Био и Савар в 1820 году выявили её на практике, Лапласу удалось сформулировать. Этот закон является основополагающим в магнитостатике. При практическом опыте рассматривался неподвижный провод с малым сечением, через который пропускали электроток. Для изучения выбирался малый участок провода, который характеризовался вектором dl. Его модуль соответствовал длине рассматриваемого участка, а направление совпадало с направлением тока.

Интересно. Лаплас Пьер Симон предложил считать током даже движение одного электрона и на этом утверждении, с помощью данного закона, доказал возможность определения МП продвигающегося точечного заряда.

Согласно этому физическому правилу, каждый сегмент dl проводника, по которому протекает электрический ток I, образовывает в пространстве вокруг себя на промежутке r и под углом α магнитное поле dB:

dB = µ0 *I*dl*sin α /4*π*r2,

Важно! Согласно закону Био-Савара-Лапласа, суммируя векторы магнитных полей отдельных секторов, можно определить МП нужного тока. Оно будет равно векторной сумме.

Существуют формулы, описывающие этот закон для отдельных случаев МП:

Формула для МП первого типа имеет вид:

Для кругового движения она выглядит так:

В этих формулах µ – это магнитная проницаемость среды (относительная).

Рассматриваемый закон вытекает из уравнений Максвелла. Максвелл вывел два уравнения для МП, случай, где электрическое поле постоянно, как раз рассматривают Био и Савар.

Принцип суперпозиции

Для МП существует принцип, согласно которому общий вектор магнитной индукции в определённой точке равен векторной сумме всех векторов МИ, созданных разными токами в данной точке:

Правило Ленца

Чтобы определить направление индукционного тока, нужно воспользоваться правилом Ленца.

Академически это правило звучит следующим образом: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Давайте попробуем чуть проще: катушка в данном случае — это недовольная бабуля. Забирают у нее магнитный поток — она недовольна и создает магнитное поле, которое этот магнитный поток хочет обратно отобрать.

Дают ей магнитный поток, забирай, мол, пользуйся, а она такая — «Да зачем сдался мне ваш магнитный поток!» и создает магнитное поле, которое этот магнитный поток выгоняет.

Электромагнитная индукция

Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

Майкл Фарадей провел ряд опытов, которые помогли открыть явление электромагнитной индукции.

Опыт раз. На одну непроводящую основу намотали две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.

При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.

Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.

Опыт три. Катушка замкнута на гальванометр, а магнит движется вдвигается (выдвигается) относительно катушки

Вот, что показали эти опыты:

Почему возникает индукционный ток?

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС.

Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Источник