в чем измеряется возраст нейтронов

ФИЗИЧЕСКИЕ ОСНОВЫ ПОЛУЧЕНИЯ ЯДЕРНОЙ ЭНЕРГИИ

Длина замедления и возраст нейтронов в среде. Дадим вначале строгое определение понятию средней длины замедления:

При замедлении одиночного нейтрона частные (не средние!) величины пространственных смещений нейтронов в процессе замедления схематически представить нетрудно (рис.5.7).

Путь, проходимый нейтроном при замедлении от энергии Е0 до энергии Ес

Точка рождения БН Точка, где энергия

Частное смещение данного нейтрона (по прямой) при замедлении до Ес

Среднеквадратичное значение этой величины – и есть длина замедления.

Рис.5.7. Графическое пояснение понятия длины замедления.

Вопрос в том, как усреднять величину пространственных смещений множества нейтронов: брать ли среднеарифметическую их величину или среднестатистическую (среднеквадратичную)?

Как показали физические эксперименты, с действительностью согласуется именно среднеквадратичная величина смещения нейтронов в процессе замедления:

В кинетической теории доказательно выводится связь средней длины замедления с другими характеристиками замедляющих свойств среды:

В теории реакторов чаще используется не сама величина средней длины замедления, а шестая часть квадрата её, названная Ферми возрастом нейтронов в среде при энергии Е.

Величина возраста обозначается греческой буквой t (E) с указанием на энергию Е замедляющихся нейтронов, которой соответствует возраст.

С учётом выражения (5.3.8) и следующего за ним выражения для величины Сs(E) формула для возраста замедляющихся нейтронов с энергией Е обретает свой окончательный вид:

Хотя несложно понять, что возраст нейтронов в среде явно находится в прямой взаимосвязи с хронологическим временем замедления нейтронов: чем больше времени идёт процесс замедления нейтрона, тем на большее расстояние смещается нейтрон в объёме среды от точки своего рождения при делении ядра.

Величина возраста для вещества (среды) характеризует меру способности этого вещества (среды) давать определённое среднеквадратичное пространственное смещение в ней замедляющихся нейтронов.

Поэтому каждое однородное вещество характеризуется своим значением возраста нейтронов любой энергии Е. В частности возраст тепловых нейтронов:

— для воды в нормальных условиях t то = 29.6 см2;

— для бериллия t то = 90 см2;

— для графита t то = 352 см2, и т.д.

а) С ростом температуры все вещества в различной степени снижают свою плотность ( g ), и ядерную концентрацию N = g NА/A; следовательно, с ростом температуры снижаются величины двух макросечений ( S s = s sN и S tr = s trN); уменьшение величин этих сечений (они стоят в знаменателе (5.3.10а)) влечёт увеличение значения возраста тепловых нейтронов. Таким образом, температурное уменьшение плотности вещества ведёт к увеличению возраста тепловых нейтронов в нём.

*) Разумеется, сказанное существенно лишь для жидких и газообразных веществ. В твёрдых реакторных материалах (топливная композиция, конструкционные материалы, твёрдые замедлители), для которых характерны крайне низкие (порядка 10-6) величины температурных коэффициентов объёмного расширения, температурно-плотностное изменение возраста тепловых нейтронов практически незаметно, но для теплоносителя (воды) плотностная составляющая температурного изменения возраста не только существенна, но и является определяющей.

Приведенные рассуждения укладываются в простую и достаточно наглядную схему качественного влияния температуры на величину возраста t т:

to ® Тн ® kTн ® Eс ® t т ¯

tо ® g ¯ ® N ¯ ® S s, S tr ¯ ® t т

Схема опосредствованного влияния температуры среды на величину возраста тепловых нейтронов.

Итак, величина возраста тепловых нейтронов в общем случае находится во власти двух конкурирующих факторов. Какой из них является превалирующим?

— В твёрдых материалах (топливная композиция, графит, циркониевый сплав, нержавеющая сталь) величина возраста тепловых нейтронов с увеличением температуры слабо уменьшается (уменьшение плотности твердых материалов крайне незначительно; влияние температуры на величину возраста тепловых нейтронов прослеживается только по верхней цепочке, через увеличение Ес);

В частности, в воде активной зоны ВВЭР при разогреве реактора от 20 до 300оС величина возраста тепловых нейтронов растёт приблизительно от 30 до 80 см2.

— средний возраст тепловых нейтронов в среде активной зоны ВВЭР, где вода занимает более половины объёма активной зоны, с ростом средней температуры активной зоны также однозначно растёт, что должно быть отнесено на счёт превалирующего влияния воды на величину возраста перед прочими материалами активной зоны.

Если быть принципиальным, то надо отметить, что с ростом давления (p) плотность воды ( g ) слабо возрастает, а потому возрастают и величины её молекулярной концентрации (N) и сечений S s и S tr, а, следовательно, величина возраста тепловых нейтронов с ростом давления немного уменьшается.

Впрочем, барометрическое изменение плотности воды незначительно, а, значит, незначительно и барометрическое изменение возраста тепловых нейтронов.

Источник

5.3.4. Длина замедления и возраст нейтронов в среде

При замедлении одиночного нейтрона частные (не средние!) величины пространственных смещений нейтронов в процессе замедления схематически представить нетрудно (рис.5.7).

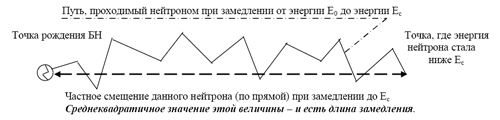Рис.5.7. Графическое пояснение понятия длины замедления.

_{— n}
l_з 2 (Е) = (1/n) Σ l_зi 2 (E) (5.3.7)
i=1


В кинетической теории доказательно выводится связь средней длины замедления с другими характеристиками замедляющих свойств среды:

_
l_з(Е) = √ ( 2C_s(E)/Σ_sΣtr ) (5.3.8)

В теории реакторов чаще используется не сама величина средней дли­ны замедления, а шестая часть квадрата её, названная Э.Ферми возрас­том нейтронов при энергии Е.

С учётом выражения (5.3.8) и следующего за ним выражения для ве­личины С_s(E) формула для возраста замедляющихся нейтронов с энергией Е обретает свой окончательный вид:

Хотя несложно понять, что возраст нейтронов в среде явно находит­ся в прямой взаимосвязи с хронологическим временем замедления нейтро­нов: чем больше времени идёт процесс замедления нейтрона, тем на боль­шее расстояние смещается нейтрон в объёме среды от точки своего рожде­ния при делении ядра.

Величина возраста для вещества (среды) определяет меру способнос­ти этого вещества (среды) давать определенное среднеквадратичное прост­ранственное смещение в ней замедляющихся нейтронов.

Поэтому каждое однородное вещество характеризуется своим значени­ем возраста нейтронов любой энергии Е. В частности возраст тепловых нейтронов:

Источник

Что такое возраст нейтронов?

Физическая природа выделения энергии при делении тяжелого ядра

Энергией связи называется энергия, которую необходимо затратить для того, чтобы расщепить ядро. Ее обычно выражают в мегаэлектронвольтах (МэВ) (1 МэВ= 1,6 · 10-13Дж). Устойчивость атомного ядра характеризуется энергией связи (Eсв).

Под энергией связи ядра понимается энергия, необходимая для полного расщепления ядра на отдельные нуклоны. Основываясь на законе сохранения энергии можно сказать, что энергия связи равняется той энергии, которая выделяется при образовании ядра из отдельных частиц.

Удельной энергией связи является энергия связи, которая приходится на один нуклон ядра. Она определяется экспериментально.

Эффективный коэффициент размножения нейтронов через возраст и длину замедления

В общем виде, когда коэффициент размножения в реакторе отличается от единицы, уравнение (3.12) запишется следующим образом:

(3.14)

τ – величина, называемая возрастом нейтронов и имеющая размерность см2.

L – длина диффузии.cм

В^2 называется геометрическим параметром

Уравнение (3.14) является основным уравнением реактора, раскрывающим зависимость эффективного коэффициента размножения нейтронов от состава и размеров активной зоны. Это уравнение справедливо для гомогенного и гетерогенного реакторов. Особенность гетерогенности активной зоны отражается в подходе к расчету параметров уравнения четырех сомножителей, а именно величин ε, φ и θ.

При стационарном процессе

(3.15)

где М2 = L2 + τ величина, называемая площадью миграции, см2

Решение уравнения (3.11) дает возможность определить величину В2. В данном случае этот параметр является функцией размеров и геометрической формы активной зоны. В частности, для цилиндрического реактора

(3.16)

Скорость ядерной реакции

N-ядерная концентрация элемента (см^-3)

Что такое возраст нейтронов?

Хотя несложно понять, что возраст нейтронов в среде явно находит­ся в прямой взаимосвязи с хронологическим временем замедления нейтро­нов: чем больше времени идёт процесс замедления нейтрона, тем на боль­шее расстояние смещается нейтрон в объёме среды от точки своего рожде­ния при делении ядра.

Продуктыреакцииделения

Условное схематическое изображение стадий процесса деления (r — расстояние между образовавшимися ядрами, t — время протекания стадий).

Деление начинается с образования составного ядра. Спустя примерно 10 −14 секунды это ядро делится на два осколка, которые, ускоряясь под действием кулоновских сил, разлетаются в противоположные стороны. Ускоренное движение осколков заканчивается спустя 10 −17 с с момента их образования. К этому времени они имеют суммарную кинетическую энергию примерно 170 МэВ и находятся на расстоянии друг от друга примерно 10 −8 см, то есть порядка размера атома.

Часть энергии деления переходит в энергию возбуждения осколков деления, которые ведут себя как любые возбуждённые ядра — либо переходят в основные состояния, излучая гамма-кванты, либо испускают нуклоны и превращаются в новые ядра, которые также могут оказаться в возбуждённом состоянии и их поведение будет аналогично поведению ядер, образовавшихся при делении исходного составного ядра.

Испускание ядром нуклона возможно лишь в случае, когда энергия возбуждения превышает энергию связи нуклона в ядре, тогда он испускается с большей вероятностью, чем гамма-квант, так как последний процесс протекает гораздо медленнее (электромагнитное взаимодействие намного слабее ядерного). Чаще всего испускаемым нуклоном является нейтрон, так как ему не нужно преодолевать кулоновский барьер при вылете из ядра, а для осколков деления это ещё вероятнее, так как они перегружены нейтронами, что приводит к понижению энергии связи последних. Энергия возбуждения осколков деления примерно равна 20 МэВ, что намного больше энергии связи нейтронов в осколках, а следовательно возможно испускание одного или двух нейтронов каждым из осколков спустя 10 −17 −10 −14 секунды с момента их образования. В результате практически мгновенно после деления составного ядра осколки деления испускают два или три нейтрона, которые принято называть мгновенными.

Образовавшиеся ядра по-прежнему находятся в возбуждённых состояниях, однако в каждом из них энергия возбуждения меньше энергии связи нейтрона, поэтому остатки энергии возбуждения излучаются в виде гамма-квантов спустя 10 −14 −10 −9 секунды с момента испускания нейтронов, такие гамма-кванты также называются мгновенными.

В дальнейшем движение осколков деления не связано с их превращениями. Так как они увлекают за собой не все электроны исходного атома, из них образуются многозарядные ионы, кинетическая энергия которых тратится на ионизацию и возбуждение атомов среды, что вызывает их торможение. В результате ионы превращаются в нейтральные атомы с ядрами в основных энергетических состояниях. Такие атомы называются продуктами деления.

Дата добавления: 2018-05-12 ; просмотров: 1154 ; Мы поможем в написании вашей работы!

Источник

Модель непрерывного замедления. Возраст нейтронов

В гл. 2 была рассмотрена диффузия моноэнергетических нейтронов (подразумевались тепловые) в среде конечных размеров. Обмен энергий с ядрами при этом не учитывался, и все нейтроны имели одну и ту же энергию после любого числа столкновений. В дальнейшем (гл. 3) рассматривалось замедление нейтронов в бесконечной однородной и гомогенной среде с равномерно распределенными источниками, т. е. в отсутствие диффузии нейтронов. Такое изложение в первую очередь обусловлено стремлением более наглядно представить физическую сущность процессов диффузии и замедления. Необходимо также отметить, что в чаще всего преобладающую роль играет лишь один из этих процессов. Тем не менее, при вычислении распределения плотности нейтронов ядерном реакторе нельзя разделять процессы диффузии и замедления.

Конечно, было бы желательно неким образом совместить эти модели. Существует несколько способов нахождения пространственного распределения замедляющихся нейтронов. Вначале остановимся на сравнительно простом, основанном на модели непрерывного замедления.

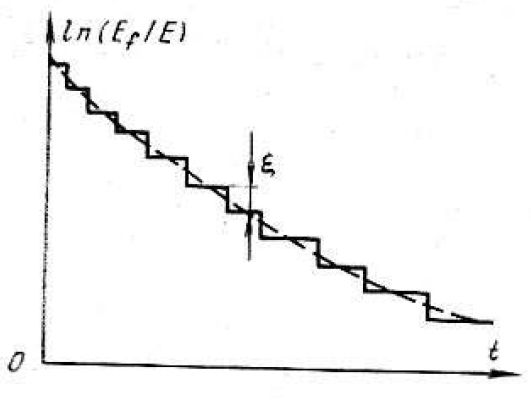
Суть этой модели удобно выяснить с помощью рис. 3.5, на котором представлена качественная зависимость 1n (E_f/E) от времени t.

Рис. 3.5 Зависимость 1n (E_f/E) от времени t

Примем, что все нейтроны, диффундировавшие в течение времени tпосле рождения, имеют скорость v. Тогда число столкновений, испытываемых одним нейтроном за время dt, равно vdt/λ_s. В то же время число столкновений нейтрона в интервале энергии dE есть dE/ ζE, а в шкале летаргии (du/ ζ) .

Иначе говоря, мы связываем через число столкновений dn переменные времени и энергии(летаргии):

При отсутствии источников и поглощения нейтронов уравнение диффузии для плотности нейтронов n(r,t) примет вид:

Имея связь времени t с летаргией u перейдем в последнем уравнении от плотности n(r, t) к плотности n(r, и). Поскольку

Здесь Ф(г, u)=vn(r,u)-поток нейтронов на единицу интервала летаргии. Величина, стоящая в квадратных скобках, есть плотность замедления q(r, и)— плотность замедления в среде без поглощения.

Ее по-другому называют поток нейтронов по энергетической оси – это другое определение – плотность замедления нейтронов или поток нейтронов по энергетической оси.

Теперь вместо летаргии и введем новую независимую переменную, называемую возрастом нейтронов:

τ(u) = 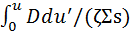(3.13a)

Эквивалентное определение в дифференциальной форме:

dτ(u)/du = 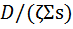(3.13б)

Тогда уравнение (3.12) запишется в виде :

Это уравнение и называется уравнением возраста(в среде без поглощения).

В среде с источниками оно примет вид

Δq(r, τ)=∂q(r, τ)/∂τ +S(r) δ(τ) (3.14б)

Для сред с поглощением математический аппарат усложняется, но смысл основных понятий не меняется.

Для сред и источников вводятся специальные граничные условия.

Возраст нейтронов τ был введен чисто формально при выводе уравнений возраста и замедления и определяется выражением (3.13а-б).

Однако он имеет и физический смысл и, более того, его можно измерить в эксперименте.

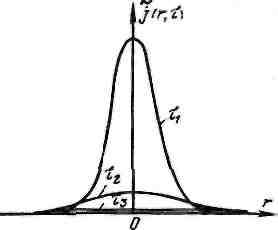
Физический смысл. На рис. 3.6 показано распределение плотности замедления j(r, τ) вблизи точечного источника (τ₁ 3/2 в точке, где расположен источник. Поэтому, когда возраст τ мал (энергия нейтронов близка к энергии нейтронов источника), кривая оказывается высокой и узкой. По мере замедления нейтронов (τ увеличивается) кривая становится более низкой и размытой. Такого характера кривых следует ожидать и из физических соображений. Нейтроны больших энергий (кривая τ₁ ) испытали в среде мало столкновений и не успели продиффунднровать далеко от источника. Нейтроны, замедлившиеся до низких энергий (большие τ), испытали много столкновении, успели продиффунднровать на значительные расстояния и распределены в среде более или менее равномерно (кривая τз). Естественно, площадь под кривой при всех значениях т остается постоянной. Это означает, что число нейтронов всех энергий в единицу времени одинаково и равно S_T.

Рис. 3.6 Распределение плотности замедления j(r, τ) вблизи точечного источника (τ₁ 2 (τ)> =6 τ

Следовательно, возраст нейтронов есть 1/6 среднего квадрата расстояния (по прямой), на которое смещается нейтрон при замедлении от энергии источника (соответствующего нулевому возрасту) до данной энергии, отвечающей возрасту τ.

Источник

ФИЗИЧЕСКИЕ ОСНОВЫ ПОЛУЧЕНИЯ ЯДЕРНОЙ ЭНЕРГИИ

Познакомимся с ещё одной комплексной характеристикой замедляющих свойств различных сред, называемой возрастом нейтронов, поскольку именно она является ключевым понятием теории замедления и чаще иных характеристик встречается в формулах и уравнениях теории реакторов.

Путь к пониманию этой характеристики проходит через понятия анизотропии рассеяния и транспортного макросечения вещества.

Анизотропия рассеяния и её мера. Ранее (п.2.4.1) мы уже познакомились с понятием средней длины свободного пробега рассеяния нейтронов:

величиной, обратной макросечению рассеяния среды. Эта величина в нашем понимании ассоциируется со средним расстоянием по прямой, проходимым нейтроном между двумя последовательными рассеяниями.

рассеивается нейтрон Следующее ядро, на котором

происходит рассеяние нейтрона

Длина пробега рассеяния l s

Рис.5.2. Схематическое изображение двух последовательных рассеяний нейтрона и средняя

длина свободного пробега рассеяния в образно-механическом представлении.

Но (вспомнить п.2.1.2) акт одиночного рассеяния является полноправной нейтронной реакцией, начинающейся с проникновения нейтрона в ядро, образования возбуждённого составного ядра, и заканчивающейся испусканием нейтрона возбуждённым ядром. Поэтому, ставя вопрос о пробеге нейтрона между последовательными рассеяниями, уместно вначале задать вопрос: сколько времени нейтрон будет находиться в составе возбуждённого ядра, и куда будет двигаться это возбуждённое ядро в течение этого времени?

Если одиночное рассеяние нейтрона в любом направлении равновероятно, то, очевидно, что после большого множества рассеяний нейтрон окажется вообще неспособным на какое-то заметное смещение в пространстве. Ведь если каждому направлению испускания нейтрона после рассеяния на одном ядре соответствует с той же вероятностью противоположное направление испускания в одном из последующих рассеяний на иных ядрах, то это значит, что мечущийся во всех мыслимых направлениях нейтрон «скачет» около одной фиксированной точки пространства среды, не сдвигаясь относительно этой точки, подобно неопытному туристу в лесу, ежеминутно меняющего направления, но не могущего удалиться от той точки леса, где он впервые обнаружил, что заблудился.

А если же нейтрон имеет какое-то закономерно-предпочтительное направление после рассеяния, то в процессе последовательных рассеяний на ядрах среды он будет постепенно удаляться от точки первого рассеяния в этом предпочтительном направлении.

Понятно, что на вопрос о равно- или неравновероятности рассеяния нейтрона по различным направлениям дать точный доказательный ответ мы не в состоянии: одиночные нейтроны пока не наблюдались даже с помощью самого современного электронного микроскопа. Поэтому судить о вероятностях рассеяния нейтрона в разных направлениях можно только на основе косвенных признаков, фиксируемых в тонких физических экспериментах.

Пространственное смещение нейтронов в процессе их рассеяния установлено как непреложный факт, и это потребовало теоретических объяснений. Поскольку принципиальных или логических противопоказаний к любому направлению рассеяния нейтрона ядром нет, условились считать, что покоящиеся ядра испускают рассеянные нейтроны равновероятно по всем возможным направлениям (в пределах 4 p стерадиан телесного угла). Коротко такое рассеяние называют изотропным.

Рис.5.3. Упрощенные (плоские) схемы изтропного и анизотропного рассеяния.

Всякое другое рассеяние, то есть такое, при котором определённые направления испускания рассеянных ядрами нейтронов оказываются более вероятными, чем другие, называется анизотропным.

В качестве направления начала отсчёта углов рассеяния обычно выбирается направление движения нейтрона до рассеяния.

Углом рассеяния ( y ) в системе координат, жёстко связанной с реактором, называют угол между направлениями движения нейтрона после и до рассеяния (рис.5.4).

Положение ядра в рассеяния

Нейтрон до рассеяния момент столкновения

Рис.5.4. Иллюстрация к понятию плоского угла рассеяния.

Мерой анизотропии рассеяния служит средний косинус угла рассеяния:

Ясно, что при изотропном рассеянии p( y ) = idem и cos y = 0, а при анизотропном рассеянии средний косинус угла рассеяния не равен 0.

Из кинетической теории следует, что величина среднего косинуса угла рассеяния определяется только массовым числом ядра-рассеивателя:

Выражение (5.3.3) недвусмысленно говорит о том, что тяжёлые ядра (с большим массовым числом А) рассеивают нейтроны практически изотропно (например, для урана-235 m = 0.0028 » 0), в то время как лёгкие ядра в рассеяниях нейтронов существенно анизотропны (например, для ядра водорода 1Н1 m = 0.667, то есть существенно отличается от нуля).

Источник