в чем измеряется вес в физике в системе си
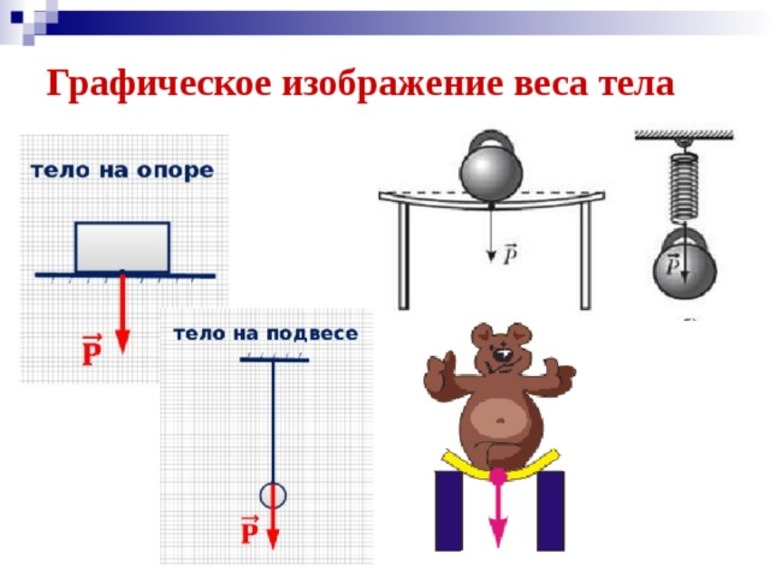
Вес тела
Невесомость: что это такое
Невесомость — это состояние, при котором тело не давит на опору или подвес.
Само слово «невесомость» как бы подсказывает нам, что веса здесь быть не должно. При этом непонятно, что с ним тогда происходит. Давайте разбираться.
Вес тела
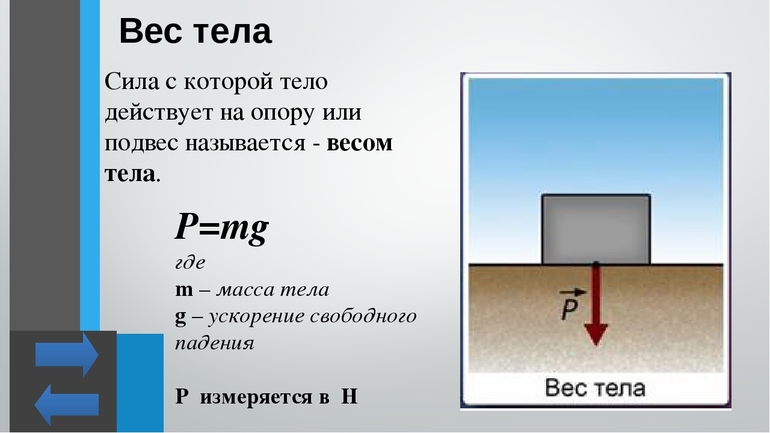
Вес — это сила, с которой тело действует на опору или подвес. Измеряется вес, как и любая другая сила, в Ньютонах.
«Но погодите! Вес же измеряют в килограммах — я вот вешу 50»
Это не совсем верно. В быту мы часто подменяем понятие «масса» понятием «вес» и говорим: вес чемодана — десять килограммам. В физике это два совершенно разных понятия, которые при этом взаимосвязаны.
Если у вас неподалеку есть весы — приглашаем в эксперимент! Один нюанс: наша затея сработает именно с механическими весами, но не с электронными. Поехали!
Шаг 1. Если встать на весы ровно и не двигаться — ваш вес будет высчитываться по формуле:
P = mg
g — ускорение свободного падения [м/с2]
На планете Земля g = 9,8 м/с2
Здесь может возникнуть два возражения:
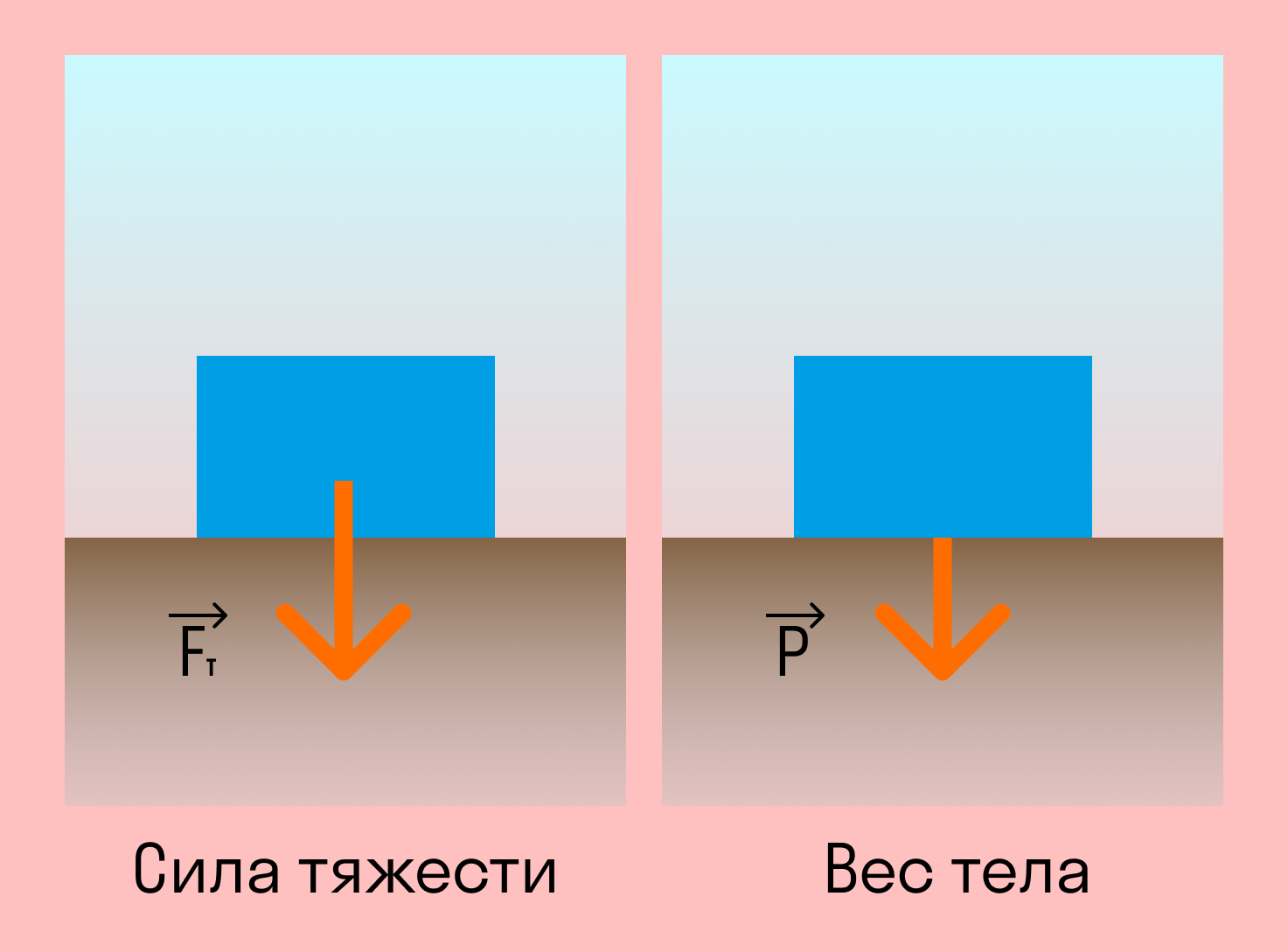
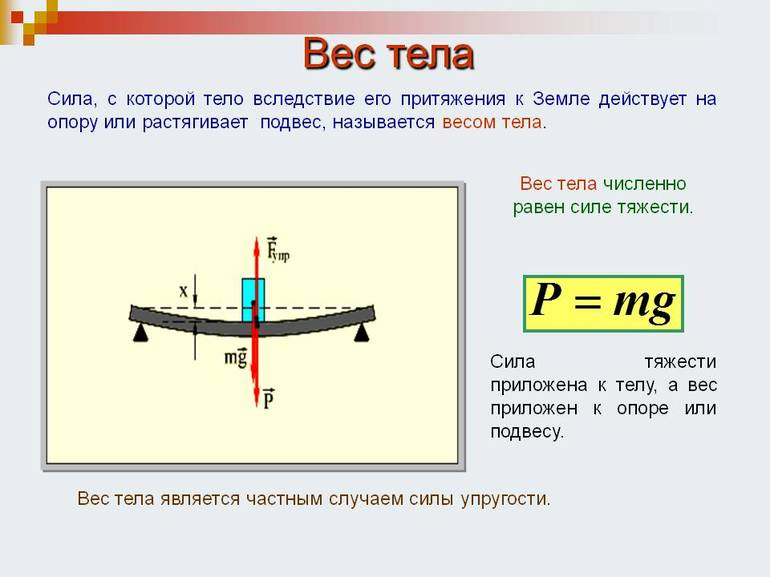
Точка приложения силы. Эта формула и правда аналогична силе тяжести. Вес тела в состоянии покоя численно равен массе тела, разница состоит лишь в точке приложения силы.
Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.
Весы измеряют силу. Весы работают таким образом, что измеряют вес тела — силу, с которой мы на них действуем, а показывают — массу. Можно сделать вывод, что весы — это динамометр (прибор, измеряющий силу).
Шаг 2. Теперь пошалим и резко встанем на носочки! Стрелка резко отклонилась влево, а потом вернулась на место. Вы придали себе ускорение, направленное вверх — в то время, как ускорение свободного падения всегда направлено к центру Земли (вниз).
Теперь вес тела вычисляем по формуле:
P = m (g-a)
g — ускорение свободного падения [м/с2]
a — ваше ускорение [м/с2]
На планете Земля g = 9,8 м/с2
Шаг 3. Последняя часть эксперимента — резко опуститься на пятки. Теперь вы сильнее давите на весы, потому что придали ускорение, направленное вниз. Стрелка весов отклонится вправо и вернется на место, когда вы придете в состояние покоя.
Формула веса примет вид:
P = m (g+a)
g — ускорение свободного падения [м/с2]
a — ваше ускорение [м/с2]
На планете Земля g = 9,8 м/с2
Кстати, если ровно стоять на весах, но взвешиваться в лифте — все будет работать наоборот. Если лифт едет вверх, то он как будто давит весами на человека, стоящего на них, а это как раз ситуация с увеличением веса. А если вниз — весы как будто бы от вас «убегают», чтобы показать меньшее значение.
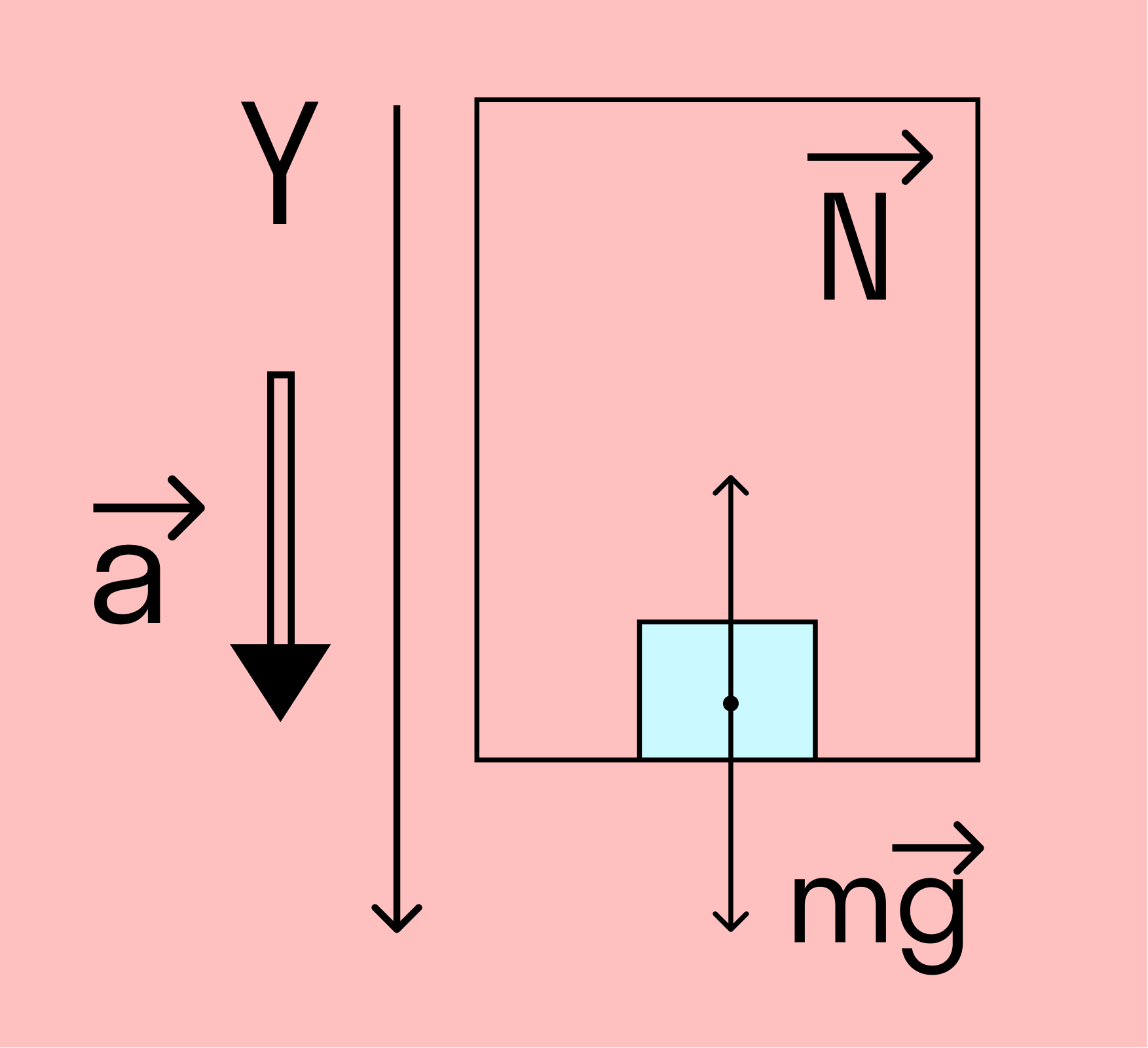
Этот случай мы можем описать через 2 закон Ньютона. Возьмем лифт, который едет вниз. Обозначим силы на рисунке.
N – сила реакции опоры [Н];
mg – сила тяжести [Н];
a – ускорение, с которым движется лифт [м/с2].
При проецировании на ось y, направленную вниз, мы получаем:
А теперь нам понадобится третий закон Ньютона — по нему сила реакции опоры равна весу тела:
Снова невесомость
Ну что, с весом разобрались. А теперь давайте сделаем так, чтобы его не стало и получилась та самая невесомость.
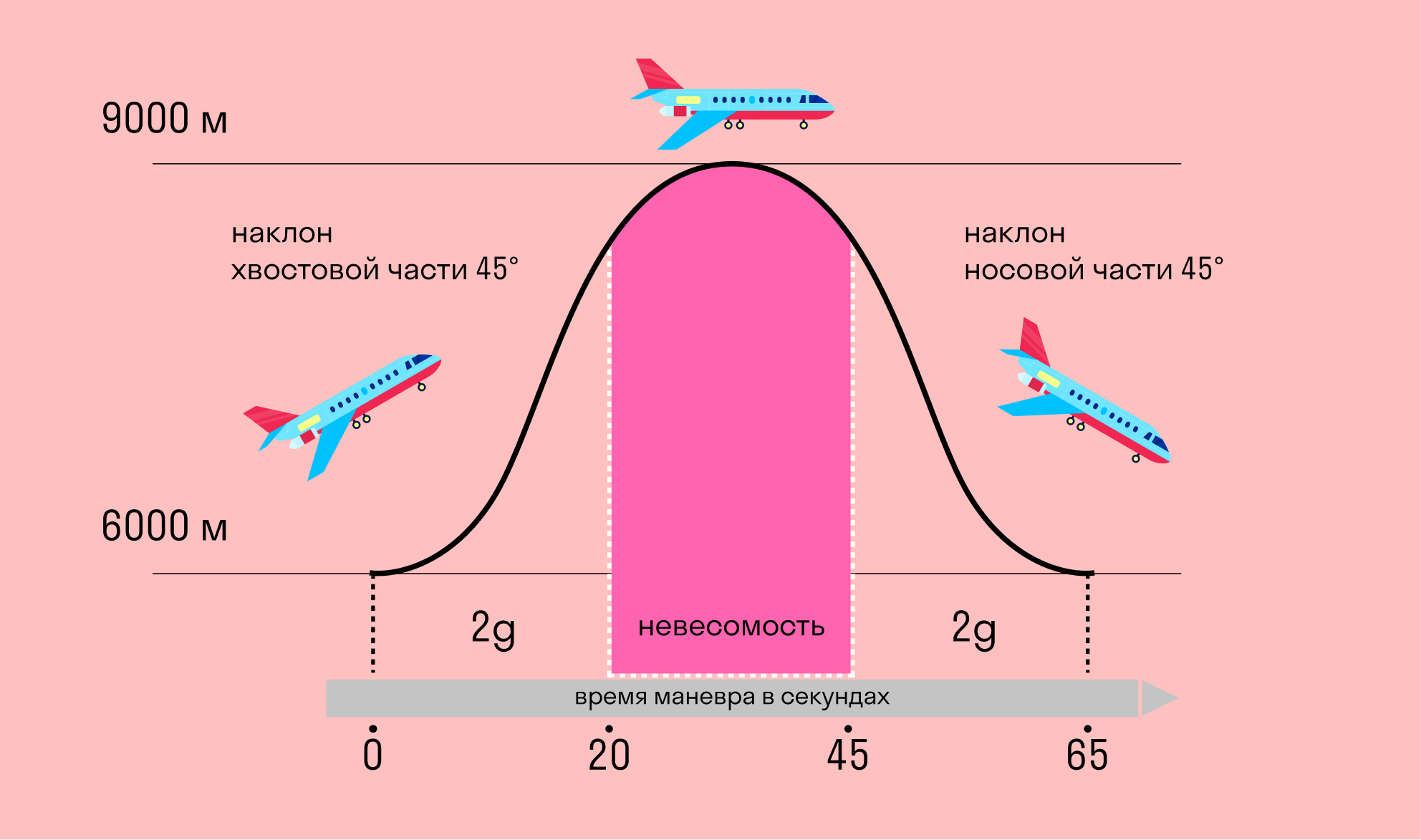
Чтобы привыкнуть к ощущению невесомости в космосе, космонавты тренируется в специальных самолетах-лабораториях:
Он взлетает и начинает просто падать, чтобы ускорение самолета было равно ускорению свободного падения. В этот момент, в формуле веса из g вычитается равное ему значение и получается 0:
Вот мы и в невесомости!
Если они летят вокруг Земли, то да. Как писал Дуглас Адамс в книге «Автоспом по галактике»: «Летать просто. Нужно просто промахнуться мимо Земли».
Когда космический корабль обращается вокруг Земли, он просто пытается на нее упасть, но промахивается. Такой процесс происходит, когда корабль движется с первой космической скоростью, равной 7.9 км/с. Это та скорость, с которой корабль становится искусственным спутником Земли.
Кстати, есть еще вторая и третья космические скорости. Вторая космическая скорость — это скорость, которая нужна, чтобы корабль стал искусственным спутником Солнца, а третья — чтобы вылетел за пределы солнечной системы. Такие дела 🙂
Понятие и определения
Массой (обозначается буквой m) называют одну из физических величин, таких, как объём, определяющих количество вещества в объекте. Существует несколько явлений, которые позволяют её оценить. Среди теоретиков есть мнение, что некоторые из этих явлений могут быть независимы друг от друга, но в ходе экспериментов не обнаружено различий в результатах от способа измерений массы:
Человек чувствует свою массу находясь в контакте с другой поверхностью. Это может быть стулом, земной твердью, креслом космонавта во время ускорения в ракете. В этих примерах речь идёт о величине, которую физики называют весом, а субъективно воспринимающимся как кажущийся вес.
Он равен фактической измеряемой массе почти во всех бытовых случаях, за следующими исключениями:
Гравитационный подход
В большинстве случаев при определении понятия веса (принятое обозначение — P, по-латински пишется как pondus) оперируют так называемым гравитационным определением. В учебниках физики формула веса для тела описывает величину как силу, действующую на объект в результате земного притяжения. На языке математики это определяется выражением P=mg, где:
Из формулы вытекает, в чём измеряется вес: количественно он рассчитывается в тех же единицах, что и сила. Поэтому, согласно Международной системе единиц (СИ), P измеряется в Ньютонах.
Гравитационное поле Земли не является однородным и варьируется в пределах 0,5% по поверхности планеты. Соответственно, величина g также непостоянна. Общепринятым считается значение, называемое стандартным и равное 9,80665 м/с2. В различных местах на поверхности Земли фактическое ускорение свободного падения составляет (м/с2):
В 1901 году третья Генеральная конференция по весам и мерам установила: вес означает количество такой же природы, что и сила, То есть определила его как вектор, так как сила — векторная величина. Тем не менее некоторые школьные учебники физики и сейчас принимают P за скаляр.
Контактное определение
Другой подход описывает явление с позиции понимания какую силу называют весом тела. В этом случае P определяется процедурой взвешивания и означает силу, с которой объект действует на опору. Этот подход предполагает различие результатов в зависимости от деталей.
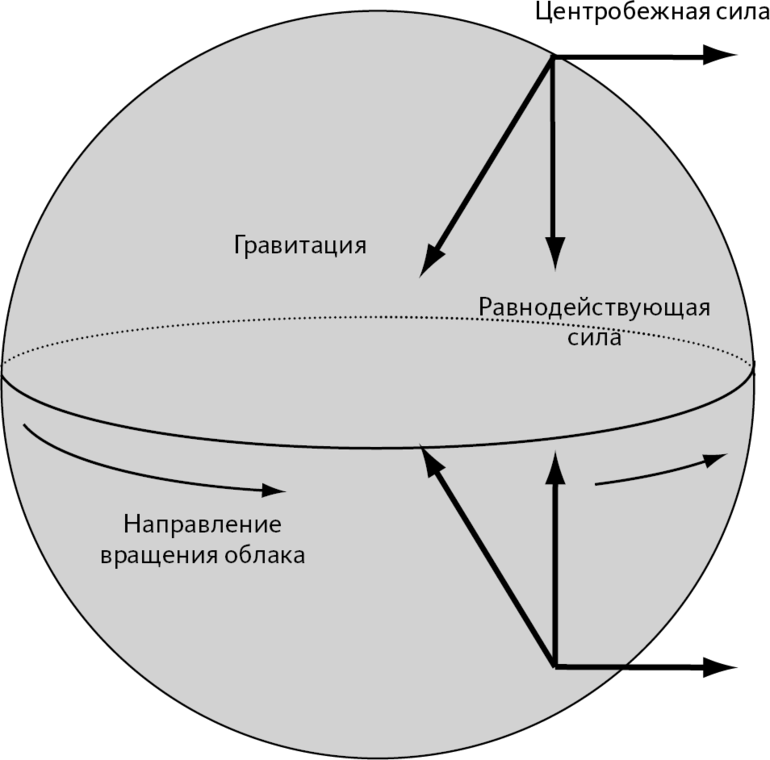
Например, объект в свободном падении оказывает незначительное воздействие на опору, однако, нахождение в невесомости не меняет вес в соответствии с гравитационным определением. Следовательно, подобный подход требует нахождения исследуемого тела в состоянии покоя, под действием стандартной гравитации без влияния центробежной силы вращения Земли.
Кроме того, контактное определение не исключает искажения от плавучести, которое уменьшает измеренный вес объекта. В воздухе на тела также действует сила, аналогичная влияющей на погружённое в воде. Для объектов с низкой плотностью эффект влияния становится более заметен. Примером тому может служить наполненный гелием воздушный шар, обладающий отрицательным весом. В общем смысле любое воздействие оказывает искажающий эффект на контактный вес, например:
История понятия
Понятия тяжести и лёгкости в качестве неотъемлемых свойств физических тел упоминаются ещё древнегреческими философами. Платон описывал вес как естественную тенденцию предметов к поиску себе подобных. Для Аристотеля лёгкость была свойством в восстановлении порядка основных элементов: воздуха, земли, огня и воды. Архимед рассматривал вес как качество, противоположное плавучести. Первое контактное определение было дано Евклидом, описывающее величину как лёгкость одной вещи по сравнению с другой, измеряемую балансом.
Когда средневековые учёные обнаружили, что на практике скорость падающего предмета со временем возрастала. Они изменили концепцию веса для сохранения причинно-следственных связей между явлениями. Понятие было разделено для тел в состоянии покоя и находящихся в гравитационном падении.
Значительных результатов в теории добился Галилей, пришедший к выводу, что величина пропорциональна количеству вещества в объекте, а не скорости его движения, как предполагала Аристотелева физика. Открытие Ньютоном закона всемирного тяготения привело к принципиальному отделению веса от фундаментального свойства объектов, связанных с инерцией. Факторы окружающей среды и плавучесть учёный считал искажением условий измерения. Для подобных обстоятельств он ввёл термин кажущийся вес.
В XX веке ньютоновские концепции абсолютного времени и пространства были поставлены под сомнение работами Эйнштейна. Теория относительности поставила всех наблюдателей, движущихся и ускоряющихся, в разные условия. Это привело к двусмысленности относительно того, что именно подразумевается под массой, которая вместе с гравитационной силой стала по существу зависящей от системы отсчёта величиной.
Неоднозначности, порождённые относительностью, привели к серьёзным дебатам в педагогическом сообществе о том, как определять вес для учеников и что им должно называться. Выбор стал лежать между пониманием его как силы, вызванной гравитацией Земли, и контактным определением, вытекающим из акта взвешивания.
Различия с массой
Путаница в понимании того, чем отличается масса от веса, свойственна для людей, не изучающих физику подробно. Этому есть простое объяснение — как правило, эти термины используются в повседневной жизни взаимозаменяемо. В общем случае, если тело находится на поверхности земли и неподвижно, значение массы будет равно скаляру веса в килограммах. Таблица, проясняющая разницу между понятиями, выглядит так:
| Масса | Вес |
| Является свойством материи. Постоянна всегда. | Зависит от действия силы тяжести. |
| У материального объекта никогда не бывает равна нулю. | Может быть равен нулю при определённых условиях. |
| Не меняется в зависимости от местоположения. | Уменьшается или увеличивается в разных местах Земли или в зависимости от высоты над её поверхностью. |
| Является скалярной величиной. | Вектор с направлением к центру земли или к другому гравитационному центру. |
| Может быть измерена с помощью баланса | Измеряется с помощью пружинных весов. |
| Как правило, измеряется в граммах и килограммах. | Единица у силы и веса одна — Ньютон (обозначается как Н) |
Главное отличительное свойство массы заключается в том, что для классической динамики она является конкретной инвариантной величиной для каждого тела. Общая теория относительности описывает переход массы в энергию и наоборот.
Обычно численное значение между m и P на Земле строго пропорционально. На бытовом уровне чтобы узнать вес тела с известной массой, достаточно помнить, что объекты обычно весят в ньютонах приблизительно в 10 раз больше значения m в килограммах.
Способы измерения
Фактически вес можно измерить как силу реакции опоры на массу, появляющуюся в точке приложения. Величина возникновения этой силы по значению равна искомому P. Определить её можно с помощью пружинных весов. Поскольку сила тяжести, вызывающая фиксируемое отклонение на шкале, может варьироваться в разных местах, значения также будут отличаться. Для стандартизации измерительные приборы такого типа всегда калибруются на 9,80665 м/с2 в заводских условиях, а затем повторно в том месте, где будут использоваться.
Для измерения массы применяют рычажный механизм. Поскольку любые изменения в гравитации будут одинаково воздействовать на известные и неизвестные массы, балансный способ позволяет иметь в результате одинаковые значения в любом месте Земли. Весовые коэффициенты в этом случае калибруются и маркируются в единицах массы, поэтому балансировочный рычаг позволяет найти массу, сравнивая воздействие притяжения на искомый объект с воздействием на эталон.
При отсутствии гравитационного поля вдали от крупных астрономических тел, баланс рычага работать не будет, но, например, на Луне он покажет те же значения, что и на Земле. Некоторые подобные инструменты могут быть размечены в единицах веса, но, поскольку они калибруются на заводе-изготовителе для стандартной гравитации, то будут показывать P для условий, под которые они настроены.
Это значит, что рычажные весы не предназначены для измерения локальной силы тяжести, воздействующей на объект. Точный вес можно определить расчётным путём, умножив массу на значение локальной гравитации из соответствующих таблиц.
На других планетах
В отличие от массы, вес тела в разных местах варьируется в зависимости от изменения значения гравитационного ускорения. Величина силы притяжения на других планетах, как и на Земле, зависит не только от их массы, но и от того, насколько удалена поверхность от центра тяжести.
В таблице ниже приведены сравнительные гравитационные ускорения на других планетах, Солнце и Луне. Под поверхностью для газовых гигантов (Юпитер, Сатурн, Уран и Нептун) подразумеваются их внешние облачные слои, для Солнца — фотосфера. Значения в таблице указаны без учёта центробежного вращения и отражают фактическую гравитацию, наблюдаемую вблизи полюсов.
| Астрономический объект | Насколько гравитация превышает земную | Поверхностное ускорение м/с2 |
| Солнце | 27,9 | 274,1 |
| Меркурий | 0,377 | 3,703 |
| Венера | 0,9032 | 8,872 |
| Земной шар | 1 | 9,8226 |
| Луна | 0,1655 | 1,625 |
| Марс | 0,3895 | 3,728 |
| Юпитер | 2,64 | 25,93 |
| Сатурн | 1,139 | 11,19 |
| Уран | 0,917 | 9,01 |
| Нептун | 1,148 | 11,28 |
Для того чтобы получить собственный вес на другой планете, необходимо просто умножить его на число кратности из соответствующего столбика. Чем ближе к центру планеты делать замер, тем значение будет выше, и наоборот. Поэтому, несмотря на то что сила притяжения Юпитера из-за огромной массы в 316 раз превышает земную, вес на уровне облаков, из-за большой их удалённости от центра масс, выглядит не таким впечатляющим, как можно было бы ожидать.
Ещё один интересный эффект, называемый невесомостью, характерный не только для космоса. Его можно наблюдать при различных обстоятельствах и на Земле. Например, при свободном падении нет опоры, к которой была бы приложена сила, а значит вес будет равен нулю, несмотря на присутствие ускорения силы тяжести и массы.
Подобный феномен происходит с космонавтами Международной космической станции на орбите Земли. Фактически она всегда падает вместе со своими обитателями на поверхность планеты, поэтому её обитатели постоянно находятся в состоянии невесомости.
Таким образом, главное правило, объясняющее наблюдаемые феномены и позволяющее избежать путаницы с массой, выглядит так: значение P всегда измеряется с помощью контактных весов, помещённых между объектом и опорной поверхностью. Именно поэтому тело, размещённое на весах и падающее вместе с ними, не будет давить на прибор, а шкала, соответственно, покажет нулевое значение.
Единицы измерения массы.
Всякое свойство тел выражается определенной величиной. Одно из важнейших свойств тела – инертность, от которой зависит его ускорение в результате взаимодействия с другими телами. Количественной мерой инертности тела является масса тела. Чем больше масса тела, тем меньшее ускорение оно получит при взаимодействии. Обозначив массы взаимодействующих тел через m1 и m2, можем предположить, что
Отношение модулей ускорений двух взаимодействующих тел равно обратному отношению их масс.
Измерив модули ускорений тела и эталона, можно найти отношение массы тела к массе эталона, которое будет равно отношению модуля ускорения эталона к модулю ускорения тела при их взаимодействии:
Массу тела можно выразить через массу эталона:
Однако, этот способ неудобен и на практике обычно неудобен. Более удобно измерять массу взвешиванием. Этот метод основан на том, что действующая на тело сила тяжести и масса этого тела пропорциональны друг другу:
Силу тяжести можно измерить на весах, так как она равна весу тела, если весы вместе с взвешиваемым телом покоятся относительно Земли. Измерив вес тела пружинными весами и зная ускорение свободного падения в месте, где производится взвешивание, можно вычислить массу:

Более удобным способом является взвешивание на рычажных весах, где сравнивают вес тела и гирь. В уравновешенном состоянии можно утверждать, что вес тела равен весу гирь, следовательно равны и их массы. Поскольку на гирях указаны их массы, то масса тела определяется суммой масс гирь.
Однако, невозможно взвешиванием измерить массу небесных тел или, наоборот, очень малые массы – атомы и частицы, из которых они состоят.
Масса тела обладает интересным и важным свойством: она зависит от того, как движется тело. Масса тела растет с увеличением его скорости. Однако, заметным это становится только при скоростях, близких к скорости света. Но с такими скоростями обычные тела не движутся.
За единицу массы в СИ принята масса специального эталона из сплава иридия и платины, которая называется килограммом (кг).
Что является единицей массы в международной системе
Единицы измерения массы в физике
Что является основной
Определение «массы», как меры количества вещества, было введено Ньютоном. До этого исследователи оперировали понятием веса. В своем труде «Математические начала натуральной философии» (1687 г.) Ньютон сначала определил «количество материи» в физическом теле как произведение его плотности на объем.
Далее он указал, что в том же смысле будет использовать термин «масса». Ньютон ввел массу в законы физики: сначала во второй закон Ньютона (через количество движения), а затем и в закон тяготения.
Масса — скалярная физическая величина, определяющая гравитационные и инерционные свойства тел. Масса — одна из основных величин в системе единиц, имеющая эталон.
Очень часто путают понятия масса и вес. Вес — это сила, с которой тело действует на опору или подвес (векторная величина). Масса же не имеет направления, а является характеристикой. Для конкретного тела масса всегда остается постоянной. Для простого тела масса напрямую связана с плотностью и образована суммой всех частичек этого тела.
Чтобы узнать массу, можно умножить плотность на объем тела и получить искомое значение массы. В бытовых условиях проще всего ее узнать с помощью обычных весов, но не стоит забывать, что весы имеют погрешность измерения.
Метрическая система
Метрическая система — общее название международной десятичной системы единиц, основанной на использовании метра и килограмма.
Основное отличие метрической системы от применявшихся ранее традиционных систем заключается в использовании упорядоченного набора единиц измерения. В этой системе для любой физической величины существует лишь одна главная единица и набор дольных и кратных единиц, образуемых стандартным образом с помощью десятичных приставок.
В России используется метрическая система измерений. Самая малая единица измерения в метрической системе — микрограмм, самая большая — тонна.
В таблице ниже представлены основные единицы измерения массы в метрической системе.
| Единица измерения | Обозначение | Величина, принцип перевода в другие единицы |
| микрограмм | мкг | 1 мкг = 1/1000 мг = 0,001 мг |
| миллиграмм | мг | 1 мг = 1/1000 г = 0,001 г |
| грамм | г | 1 г = 1/1000 кг = 0,001 кг |
| килограмм | кг | 1 кг = 1000 г |
| центнер | ц | 1 ц = 100 кг |
| тонна | т | 1 т = 1000 кг |
Американская и Британская системы
Британская (Английская) система измерения используется в Великобритании (хотя с 1995 года в качестве официальной используется метрическая система), США, частично в Канаде. Английская система мер берет свое начало из Римской системы мер. С XX века постепенно меры английской системы вытесняются метрической системой. Фунт, унция, стоун используются одинаково в Американской и Британской системе.
В таблице представлены основные единицы измерения Британской и Американской систем.
| Единица измерения | Величина, принцип перевода в другие единицы |
| Общие единицы измерения | |
| стоун | 1 стоун = 14 фунтов = 6350,29 г (или 6,35 кг) |
| фунт | 1 фунт = 16 унций = 453,59 г |
| клов | 1 клов = 0,5 стоуна = 7 фунтам = 3,175 кг |
| унция | 1 унция = 28,35 г |
| Британская система | |
| тод | 1 тод = 28 фунтам = 2 стоунам = 12,7 кг |
| гран | 1 гран = 1/98000 стоуна = 1/7000 фунта = 1/437,5 унции = 1/27,34 драхмы = 64,80 мг |
| английская длинная тонна | 1 англ. т. = 2240 фунтов = 1016,047 кг |
| английский центнер | 1 англ. ц. = 112 фунтов = 50,80 кг |
| Американская система | |
| квартер | 1 квартер = 25 фунтам = 11,34 кг |
| квинтал | 1 квинтал = 100 фунтам = 45,36 кг |
| американская короткая тонна | 1 ам. т. = 2000 фунтов = 907,18474 кг |
| американская драхма | 1 драхма = 1/16 унции = 1/256 фунта = 1/3584 стоуна = 1,77 г |
| американский центнер | 1 ам. ц. = 100 фунтов = 45,36 кг |
Перевод единиц из одной системы в другую
Разберем несколько примеров перевода. Допустим нам нужно узнать: