в чем измеряется увеличение линзы
Формула тонкой линзы
теория по физике 🧲 оптика
Формула тонкой линзы — формула, связывающая три величины: расстояние от предмета до линзы, расстояние от изображения до линзы и фокусное расстояние линзы.
Вывод формулы
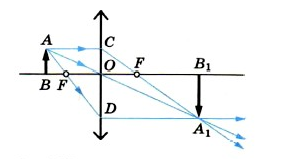
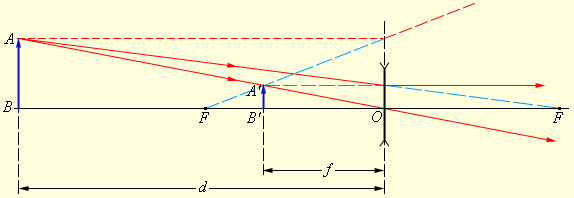
Обратимся к рисунку, который мы использовали для объяснения правила построения изображений в собирающих линзах:
Видно, что треугольники АОВ и А1В1О подобные (по двум углам). Следовательно:
По двум углам также являются подобными треугольники COF и FA1B1. Отсюда делаем вывод, что:
Линия предмета образует с частью главной оптической оси, перпендикуляром, проведенным из верхней точки к линзе, и частью самой линзы прямоугольник. Следовательно, его противоположные стороны равны:
Отсюда следует, что:
B O является расстоянием от предмета до линзы. Обозначим его за d. O B 1 является расстоянием от линзы до изображения. Обозначим его за f. O F является фокусным расстоянием линзы. Обозначим его за F. F B 1 является разностью расстояния от линзы до изображения и фокусного расстояния линзы. Поэтому это выражение мы можем записать так:
Избавимся от знаменателей и получим:
Или можно записать так:
Теперь все члены равенства поделим на произведение Ffd. В результате вычислений получим формулу тонкой линзы:
Формула тонкой линзы
Поскольку величиной, равной обратной фокусному расстоянию, является оптическая сила, формулу тонкой линзы можно записать следующим образом:
Величины d, ƒ и F могут быть как положительными, так и отрицательными. Отметим (без доказательства), что при применении формулы тонкой линзы знаки нужно ставить перед членами уравнения согласно следующим правилам.
Иногда случается, что перед величинами F, f и d знаки неизвестны. Тогда при вычислениях перед ними ставят знаки «плюс». Но если в результате вычислений фокусного расстояния или расстояния от линзы до изображения либо до источника получается отрицательная величина, то это означает, что фокус, изображение или источник мнимые.
Пример №1. Фокусное расстояние линзы равно 10 см. Найти расстояние от предмета до линзы, если расстояние от нее до изображения составляет 15 см.
Переводить в СИ единицы измерения не будем, поскольку они однородны. Так как все величины выражены в см, то и ответ будет выражен в см.
Применим формулу тонкой линзы:
Умножим выражение на 150d:
Увеличение линзы
Раньше мы уже упоминали, что изображение, полученное в линзе, может быть увеличенным или уменьшенным. Различие размеров предмета и изображения характеризуется увеличением.
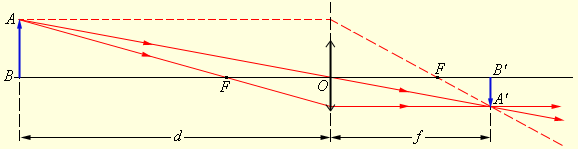
Чтобы найти линейное увеличение изображения предмета в линзе, снова обратимся к первому рисунку этого параграфа. Если высота предмета АВ равна h, а высота изображения А1В1 равна Н, то:
Мы уже выяснили, что треугольники АОВ и ОА1В1 подобны. Поэтому:
Где H — высота изображения предмета, h — высота самого предмета.
Отсюда вытекает, что увеличение линзы равно:
Пример №2. Предмет имеет высоту h = 2 см. Какое фокусное расстояние F должна иметь линза, расположенная от экрана на расстоянии f = 4 м, чтобы изображение указанного предмета имело высоту H = 1 м?
Сначала применим формулы тонкой линзы:
Она необходима, чтобы выразить фокусное расстояние линзы:
Расстояние от предмета до линзы неизвестно. Но его можно выразить из формулы увеличения линзы:
Отсюда это расстояние равно:
Подставим полученное выражение в формулу фокусного расстояния линзы:

В чем измеряется увеличение линзы
Выведем формулу, связывающую три величины: расстояние d от предмета до линзы, расстояние ƒ от изображения до линзы и фокусное расстояние F.
Из подобия треугольников АОВ и А1В1О следует равенство
Из подобия треугольников COF и FA1B1 имеем:
Учитывая свойство пропорции, имеем:
ƒF + Fd = ƒd
Поделив все члены полученного равенства на произведение Fƒd, получим
Уравнение принято называть формулой тонкой линзы.
Величины d, ƒ и F могут быть как положительными, так и отрицательными.
Применяя формулу линзы, нужно ставить знаки перед членами уравнения согласно следующему правилу.
Если линза собирающая, то ее фокус действительный, и перед членом : 
В случае рассеивающей линзы F
есть линейное увеличение.
Из подобия треугольников АОВ и ОА1В1 следует, что
Следовательно, увеличение линзы равно отношению расстояния от изображения до линзы к расстоянию от линзы до предмета:
Линзы являются основной частью фотоаппарата, проекционного аппарата, микроскопа, телескопа.
В глазу тоже есть линза — хрусталик.
Оптика. Линза. Оптическая сила линзы.
Для указания оптической силы линзы применяют латинский символ D.
где, d- дистанция от предмета до линзы;
f – дистанция от линзы до изображения.
Другими словами, чем мельче (короче) фокусное расстояние, тем значительнее оптическая сила линзы.
Потому как у рассеивающей линзы фокус мнимый, то было принято, что ее фокусное расстояние со знаком«-». Из этого получаем, что и оптическая сила для указанной линзы будет отрицательной.
Оптическую силу собирающей линзы принято указывать как положительную «+».
Оптическая сила системы, сформированной из пары размещенных в воздухе линз с оптическими силами D 1 и D 2, находится согласно выражения:
где a— дистанция между задней главной плоскостью первой линзы и передней главной плоскостью второй линзы.
В случае тонких линз a сходится с дистанцией между линзами и выражение упрощается до двух первых слагаемых.
И получаем, что суммарная оптическая сила двух либо более тонких линз определяется суммой оптических сил каждой отдельной линзы.
Как правило, оптическая сила применяется для описания характерных свойств линз, практикуемых в офтальмологии, в наименовании очков и для более простого геометрического нахождения траектории луча.
При диагностировании оптической силы линз нашли широкое применение диоптриметры, дающие возможность выполнять измерения, в том числе, астигматических и контактных линз.
Физика. 11 класс
Конспект урока
Урок 13. Линза. Построение изображения в линзе
Перечень вопросов, рассматриваемых на уроке:
1. Виды линз, их основные характеристики.
2. Построение изображений в линзах. Характеристики полученных изображений.
3. Оптическая сила линзы.
4. Формула тонкой линзы.
5. Линейное увеличение линзы.
Линза – прозрачное тело, ограниченное криволинейными поверхностями.
Оптический центр линзы – это точка, проходя через которую лучи не меняют своего направления.
Главная оптическая ось – прямая, проходящая через центры сферических поверхностей линзы.
Побочная оптическая ось – любая прямая, кроме главной оптической оси, проходящая через оптический центр.
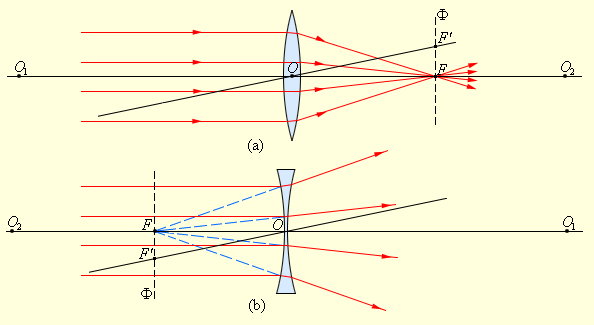
Главный оптический фокус – точка, в которой после преломления пересекаются все лучи, падающие на линзу, параллельно главной оптической оси.
Фокусное расстояние – расстояние от линзы до ее фокуса.
Фокальная плоскость – плоскость, проведенная через главный фокус перпендикулярно главной оптической оси.
Оптическая сила линзы – величина, обратная фокусному расстоянию.
Линейное увеличение – отношение линейного размера изображения к линейному размеру предмета.
Мениск – вогнуто-выпуклая или выпукло-вогнутая линза, ограниченная двумя сферическими поверхностями.
Аберрация оптической системы – искажение или погрешность изображения в оптической системе, вызываемая отклонением луча от того направления, по которому он должен был бы идти в идеальной оптической системе.
Аккомодация – приспособленность глаза к изменению внешних условий.
Адаптация – приспособление глаза к изменяющимся условиям освещения.
Близорукость – дефект зрения, при котором изображения предметов фокусируются перед сетчаткой глаза при спокойном состоянии глазной мышцы.
Дальнозоркость – дефект зрения, при котором изображения предметов фокусируются за сетчаткой глаза при спокойном состоянии глазной мышцы.
Список обязательной и дополнительной литературы:
Мякишев Г.Я., Буховцев Б.Б., Чаругин В. М.. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С.191 – 202.
Рымкевич А.П. Сборник задач по физике. 10-11 класс. М.: Дрофа,2009.
Теоретический материал для самостоятельного изучения
Простейшей оптической системой является линза.
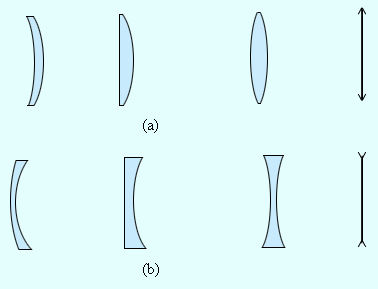
Виды линз: выпуклые и вогнутые.
Выпуклые линзы: двояковыпуклая, плоско-выпуклая, вогнуто-выпуклая.
Вогнутые линзы: двояковогнутая, плоско-вогнутая, выпукло-вогнутая.
Физической моделью реальной линзы является тонкая линза.
Если толщина линзы d пренебрежимо мала по сравнению с радиусами кривизны R1 и R2 сферических поверхностей, линзу называют тонкой
Основные элементы и характеристики тонкой линзы: оптический центр, главная оптическая ось, побочная оптическая ось, фокус, фокусное расстояние, фокальная плоскость, оптическая сила.
Основное свойство линзы: световые лучи, исходящие из какой-либо точки предмета (источника), проходя через линзу, пересекаются в одной точке (изображении) независимо от того через какую часть линзы прошли.
Чтобы построить изображение точки, расположенной на главной оптической оси, необходимо применить метод побочных осей: надо провести вспомогательную побочную оптическую ось и рассматривать данную точку как находящуюся вне проведенной оптической оси.
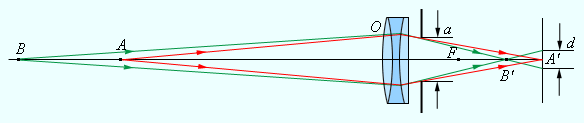
Собирающая линза может давать различные изображения в зависимости от того, на каком расстоянии d от линзы расположен предмет: увеличенное, уменьшенное, прямое, перевернутое, действительное, мнимое.
Для рассеивающей линзы положение предмета относительно линзы не имеет значения. Изображение предмета в линзе всегда мнимое, прямое и уменьшенное.
Основные формулы и уравнения:
Оптическая сила линзы:
где F – фокусное расстояние.
Или
где где R1 и R2 – радиусы кривизны поверхностей; n – показатель преломления линзы в веществе.
Оптическая сила сложной системы равна сумме оптических сил составляющих систем.
Уравнение, связывающее фокусное расстояние F, расстояние от линзы до изображения 
Линейным увеличением (Г) называется отношение линейного размера изображения (H) к линейному размеру предмета (h):
При расчетах числовые значения действительных величин всегда подставляются со знаком «+», а мнимых со знаком «-».
Если после преломления лучи, идущие от источника, пересекаются в одной точке за линзой, то они образуют действительное изображение. Изображение является мнимым, когда прошедшие через линзу лучи расходятся и изображение находится в точке пересечения их продолжений.
Линзы являются основной частью многих оптических приборов. Например, глаз, как орган зрения, тоже является уникальной оптической системой, в которой роль линзы выполняют роговица и хрусталик.
Линзы применяют на практике для получения изображений высокого качества. Однако, изображение, даваемое простой линзой, в силу ряда недостатков не удовлетворяет этим требованиям. Недостатки оптических систем, приводящие к искажению изображений на выходе из оптической системы, называются аберрациями. Виды аберраций: сферическая аберрация, хроматическая аберрация, кома, астигматизм, дисторсия.
Разбор тренировочного задания.
1. Заполните пропуски в тексте: «Лучи, падающие на рассеивающую линзу параллельно ________ оптической оси, после прохождения линзы идут так, что их ___________ проходят через _____, расположенный с той стороны линзы, откуда ______ лучи»
Варианты ответов: побочной; фокус; преломляются; продолжения; падают; центр; окончания; главной.
Правильный вариант: главной; продолжения; фокус; падают.
Подсказка: Ход лучей в тонкой линзе.
2. Фокусное расстояние тонкой собирающей линзы равно 20 см. Предмет малых размеров расположен на её главной оптической оси, при этом изображение предмета находится на расстоянии 60 см от линзы. Предмет расположен от линзы на расстоянии ___ см.
Правильный вариант: 30.
Подсказка: Формула тонкой линзы
Формула тонкой линзы:
отсюда получаем формулу для расчета расстояния от линзы до предмета:
Тонкие линзы
Линза – это прозрачное тело, имеющая 2 сферические поверхности. Она, является тонкой, если ее толщина меньше радиусов кривизны сферических поверхностей.
Линза, имеющая большую толщину по краям, называется рассеивающей.
Главная оптическая ось – это прямая, которая проходит через центры кривизны O 1 и O 2 сферических поверхностей.
Побочные оптические оси – это прямые, проходящие через оптический центр.
Эта точка получила название главный фокус линзы.
Тонкая линза имеет два главных фокуса, которые располагаются симметрично на главной оптической оси по отношению к линзе.
Фокус собирающей линзы – действительный, а у рассеивающей – мнимый.
Главным свойством линз является способность передавать изображения предметов. Они, в свою очередь, бывают:
Построение изображения в линзах
Величина D – это оптическая сила линзы, равная обратному фокусному расстоянию.
Величина d и f тоже подчиняются определенным знакам:
Линейные размеры изображения зависят от положения предмета по отношению к линзе.
Выпуклая поверхность имеет положительный радиус кривизны, а вогнутая поверхность – отрицательным. Данная формула применима в изготовлении линз с заданной оптической силой.
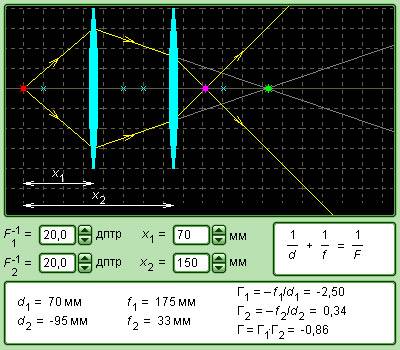
Астрономическая труба Кеплера и земная труба Галилея
Тонкая линза имеет некоторые недостатки, которые не позволяют получать изображения высокого разрешения.
Аберрация – это искажение, которое возникает в процессе формирования изображения. В зависимости от расстояния, на котором проводится наблюдение, аберрации могут быть сферическими и хроматическими.
Смысл сферической аберрации в том, что при широких световых пучках лучи, находящиеся на далеком расстоянии от оптической оси, пересекают ее не в месте фокуса. Формула тонкой линзы действует лишь для лучей, которые находятся близко к оптической оси. Изображение удаленного источника, которое создается широким пучком лучей, преломленных линзой, размыто.
Современные оптические приборы оснащены не тонкими линзами, а сложными линзовыми системами, в которых есть возможность исключить некоторые искажения.
В таких приборах, как фотоаппараты, проекторы и т.д., используются собирающие линзы для формирования действительных изображений предметов.
Что представляет собой фотоаппарат
Фотоаппарат – это замкнутая светонепроницаемая камера, в которой изображение запечатленных предметов создается на пленке системой линз – объективом. На время экспозиции объектив открывается и закрывается с помощью специального затвора.