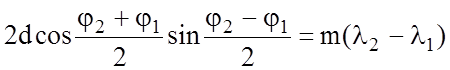в чем измеряется угловая дисперсия
Характеристики спектральных приборов. Угловая и линейная дисперсия СП. Область дисперсии СП
Страницы работы
Фрагмент текста работы
ХАРАКТЕРИСТИКИ СПЕКТРАЛЬНЫХ ПРИБОРОВ
Спектральные приборы (СП) представляют собой оптические устройства, служащие для получения и анализа спектров излучения и поглощения различных светящихся (рассеивающих) объектов. Они позволяют с большой точностью определять длины волн или разницу в длинах волн двух близких спектральных линий, измерять интенсивность того или иного участка спектра или отдельных линий.
Под спектральной линией обычно понимают изображение входной щели СП, освещаемой источником, спектральный состав которого анализируется в плоскости приемника (экран, фотоэлектронный приемник, фотопластинка, глаз). Спектром или спектральным составом излучения или поглощения называют упорядоченное расположение по длинам волн или частотам энергии излучения или поглощения исследуемого объекта.
На рис. 6.1 приведена принципиальная схема СП.
СП делятся на несколько групп по следующим оптическим характеристикам:
3) По величине обратной линейной дисперсии: малая (десятки нм/мм); средняя (единицы нм/мм), большая (десятые доли нм/мм) и высокая (сотые доли нм/мм).
6.1. Угловая и линейная дисперсия СП
Угловая дисперсия Dj характеризует скорость изменения угла отклонения спектральной линии при изменении длины волны (рис.6.2) и определяется как 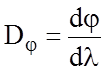
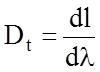
Из рисунков легко установить связь между Dj и Dl.
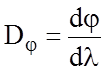
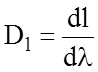
Под обратной линейной дисперсией понимается величина 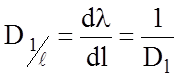
а) Дисперсия дифракционной решетки. Угловая дисперсия определяется из условия образования главных максимумов дифракционной картины dsinj = ml.
Сделав преобразования, получим:
Если l1 = l, а l2 = l + dl, и j1 = j, а j2 = j + dj, тогда окончательно dcosj×dj = mdl.
Отсюда величина угловой дисперсии выразится как
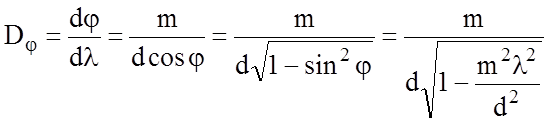
Для грубых решеток d>>l и, следовательно,
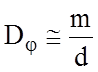
б) Дисперсия призмы. В области прозрачности вещества, из которого сделана призма, зависимость показателя преломления n от длины волны определяется формулой Коши 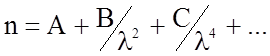
Наиболее простым диспергирующим элементом в призменных СП является трехгранная призма (рис.6.5). Она располагается обычно под углом наименьшего отклонения j, который вместе с преломляющим углом призмы y определяет функциональную связь между ними и показателями преломления вещества призмы n.
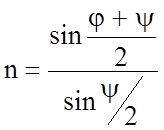
Угловая дисперсия призмы Dj в соответствии с ее определением запишется
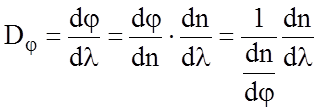
Так как 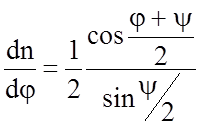
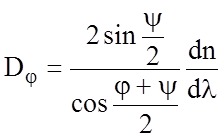
Обычно 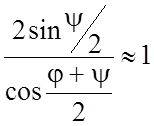
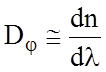
6.2. Разрешающая способность СП
Под разрешающей способностью R понимается величина, характеризующая отношение длины волны спектра l, вблизи которой необходимо определить минимальную разницу в двух длинах волн (l1 = l и l2=l + dl) dl, разрешаемую данным СП, к величине этого минимального интервала:
Угловая дисперсия спектральной призмы.



Призма, как спектральный прибор, характеризуется угловой дисперсией Dj. Угловая дисперсия представляет собой отношение разности углов отклонения dj двух спектрально близких монохроматических пучков к разности их длин волн dl:

Угловой дисперсией определяется степень растянутости спектра. Значения Dj в системе СИ измеряются в радианах на метр (рад/м). Пользуются также внесистемной единицей измерения угловой дисперсии: угловая минута на нанометр (мин/нм).
Угловую дисперсию можно непосредственно определить по формуле (10), если известны углы отклонения спектрально близких длин волн.
Согласно формуле (9), лучам различной длины волны должны соответствовать разные значения jmin, так как n = ¦(l). Примем во внимание зависимость j от n, а также зависимость n от l. Правую часть уравнения (10) умножим и разделим на dn, тогда для j = jmin

Продифференцировав формулу (9), получим

тогда (11) преобразуется как

Поскольку, как следует из формулы (9),
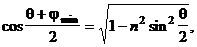
то окончательное выражение для угловой дисперсии призмы принимает вид:


Из формул (15, 16) следует, что угловая дисперсия растет с увеличением n и с увеличением дисперсии материала призмы dn/dl. Поскольку с уменьшением длины волны показатель преломления увеличивается, а также увеличивается дисперсия материала призмы (случай нормальной дисперсии), то и угловая дисперсия в области более коротких длин волн должна быть больше.
Описание установки
Угловая дисперсия спектральной призмы
Призма, как спектральный прибор, характеризуется угловой дисперсией Dj. Угловая дисперсия представляет собой отношение разности углов отклонения dj двух спектрально близких монохроматических пучков к разности их длин волн dl:

Угловой дисперсией определяется степень растянутости спектра. Значения Dj в системе СИ измеряются в радианах на метр (рад/м). Пользуются также внесистемной единицей измерения угловой дисперсии: угловая минута на нанометр (мин/нм).
Угловую дисперсию можно непосредственно определить по формуле (10), если известны углы отклонения спектрально близких длин волн.
Согласно формуле (9), лучам различной длины волны должны соответствовать разные значения jmin, так как n = ¦(l). Примем во внимание зависимость j от n, а также зависимость n от l. Правую часть уравнения (10) умножим и разделим на dn, тогда для j = jmin

Продифференцировав формулу (9), получим

тогда (11) преобразуется как

Поскольку, как следует из формулы (9),

то окончательное выражение для угловой дисперсии призмы принимает вид:


Из формул (15, 16) следует, что угловая дисперсия растет с увеличением n и с увеличением дисперсии материала призмы dn/dl. Поскольку с уменьшением длины волны показатель преломления увеличивается, а также увеличивается дисперсия материала призмы (случай нормальной дисперсии), то и угловая дисперсия в области более коротких длин волн должна быть больше.
Описание установки
В чем измеряется угловая дисперсия
30.1.(а).Освещая тонкую пленку из прозрачного материала монохроматическим светом, падающим нормально к поверхности пленки, на ней наблюдают параллельные чередующиеся равноудаленные темные и светлые полосы. Что можно сказать о толщине пленки?
30.1.(б).Что такое угловая и линейная дисперсии дифракционной решетки?
Угловая дисперсия дифракционной решетки:

• Линейная дисперсия дифракционной решетки:
Из рисунка видно, что при небольших 

собирающей дифрагирующие лучи на экране. Следовательно,
линейная дисперсия может быть выражена через угловую
дисперсию D :
Для дифракционной решетки (при небольших
30.1.(в).Что такое угол Брюстера? Чем он замечателен?
Угол, при котором происходит полная поляризация при отражении, называется углом Брюстера :

30.1 (г) Можно ли определить длину волны рентгеновского излучения и постоянную кристаллической решетки исследуемого вещества, измерив углы скольжения, при которых наблюдаются рентгеновские дифракционные пики трех смежных порядков 
Направления максимумов лежат на линиях пересечения трех косинусов, оси которых параллельны координатным осям и заданы условия:
Углы зависимы: 
Разность фаз: 

Лабораторная работа №8
ОПРЕДЕЛЕНИЕ ОСНОВНЫХ ХАРАКТЕРИСТИК ДИФРАКЦИОННОЙ РЕШЕТКИ
Теоретическая часть

Следовательно, условие возникновения главных интерференционных максимумов решетки имеет вид
В фокальной плоскости линзы для лучей, не испытавших дифракции, наблюдается центральный белый максимум нулевого порядка (φ = 0, k = 0), вправо и влево от которого располагаются цветные максимумы (спектральные линии) первого, второго и последующих порядков интерференции (см. рис. 1). Интенсивность максимумов сильно уменьшается с ростом их порядка, то есть с увеличением угла дифракции.
Уравнение (1) позволяет рассчитать период дифракционной решетки d, если измерен угол дифракции φ, соответствующий спектральной линии, для которой известны ее длина волны и порядок спектра.
Зная период решетки, легко рассчитать число штрихов, нанесенных на один миллиметр ширины решетки:

Одной из основных характеристик дифракционной решетки является ее угловая дисперсия. Угловой дисперсией решетки называется величина, определяемая приращением угла дифракции при изменении длины волны на единицу,

Дисперсия определяет угловое расстояние между направлениями двух спектральных линий, отличающихся по длине волны на 1 нм (Dl = 1 нм), и характеризует степень растянутости спектра вблизи данной длины волны. Формула для расчета угловой дисперсии решетки может быть получена при дифференцировании уравнения
определяющего положение главных максимумов:


Из этого выражения следует, что угловая дисперсия решетки тем больше, чем больше порядок спектра. Этим объясняется расширение спектра одного порядка у решеток с ростом порядка.
Для решеток с разными периодами ширина спектра больше у решетки с меньшим периодом. Обычно в пределах одного порядка Dφ меняется незначительно (особенно для решеток с небольшим числом штрихов на миллиметр), поэтому дисперсия в пределах одного порядка почти не меняется. Спектр, полученный при постоянной дисперсии, растянут равномерно во всей области длин волн, что выгодно отличает спектр решетки от спектра, даваемого призмой.
В спектроскопии принято считать, что оптический прибор разрешил две линии спектра, если изображения этих линий в спектре, полученном с помощью данного прибора, видны раздельно. Если изображения двух линий сливаются в одну, то говорят, что прибор их не разрешил. Одни и те же линии спектра могут быть разрешены одним прибором и не разрешены другим. Это связано с шириной максимумов интенсивности этих линий.
Разрешающей способностью (или разрешающей силой) принято называть способность решетки дать увидеть раздельно на экране в области длин волн l две длины волны, отличных друг от друга на Dl. Разрешающая способность является величиной безразмерной. Чем она больше, тем более близкие по длине волны линии способен разрешить прибор. По критерию Релея разрешающая способность дифракционной решетки определяется порядком спектра и полным числом штрихов решетки N:

Описание лабораторной установки
Порядок выполнения работы
Включить источник света, повернуть окуляр так, чтобы его оптическая ось совпадала с осью коллиматора. При этом в поле зрения окуляра зрительной трубы появится изображение входной щели коллиматора. Вращая окуляр, следует добиться резкого изображения щели. Установить изображение щели параллельно отсчетной нити окуляра поворотом трубы в кронштейне вокруг оптической оси, предварительно ослабив зажимной винт.
Зная период решетки, рассчитать число штрихов на 1 мм ширины решетки по формуле (2).
Произвести измерение угла дифракции для других спектральных линий из рекомендуемых ниже по заданию преподавателя. Рассчитать угловую дисперсию решетки, зная углы дифракции на разных спектральных линиях (формулы 3, 4). Сравнить результаты двух способов вычисления и сделать выводы.
Вычислить разрешающую способность по формуле 5, найти полное число штрихов решетки, зная число штрихов на 1 мм и измерив ширину нарезанной части решетки.
Вывести формулу погрешности для периода решетки и оценить ее значение в соответствии с самой величиной.
Рекомендуемые задания
| Тип решетки | Порядок | Цвета линии |
| 1 50 штр/мм | k = 1 | голубой, зеленый, красный |
| k = 2 | фиолетовый, голубой, зеленый, красный | |
| k = 3 | фиолетовый, зеленый, желтый (2линии), красный | |
| 2 100 штр/мм | k = 1 | фиолетовый, голубой, зеленый, красный |
| k = 2 | фиолетовый, зеленый, желтый (2линии), красный | |
| k = 3 | фиолетовый, зеленый, желтый (2линии), красный |