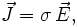в чем измеряется удельная проводимость
Удельная проводимость
Удельная проводимость
Уде́льная проводи́мость (уде́льная электропрово́дность) — мера способности вещества проводить электрический ток. (Точнее следует говорить об электропроводности среды, т.к. не имеется в виду обязательно химически чистое вещество; эта величина различна для разных веществ или смесей, сплавов и т.п.). В линейном изотропном веществе плотность возникающего тока прямо пропорциональна электрическому полю (см. Закон Ома) Удельной проводимостью называют величину, обратную удельному сопротивлению.
В неоднородной среде σ может зависеть (и в общем случае зависит) от координат, т.е. не совпадает в различных точках проводника.
В анизотропных средах формула остаётся той же, но σ является тензором 2 ранга, и векторы плотности тока и напряжённости поля, вообще говоря, не коллинеарны.
Величина, обратная удельной проводимости, называется удельным сопротивлением.
Удельная проводимость некоторых веществ
Удельной проводимостью называют величину, обратную удельному сопротивлению. (см. удельное сопротивление).
Удельная проводимость при температуре 20 °C:
| вещество | См/м |
|---|---|
| платина | 5 800 000 |
| золото | 43 470 000 |
| серебро | 62 500 000 |
| медь | 58 800 000 |
| алюминий | 36 000 000 |
| иридий | 21 090 000 |
| молибден | 18 500 000 |
| вольфрам | 18 180 000 |
| цинк | 16 940 000 |
| никель | 11 500 000 |
| железо чистое | 10 000 000 |
| иридий | 9 350 000 |
| олово | 8 330 000 |
| сталь литая | 7 690 000 |
| свинец | 4 810 000 |
| нейзильбер | 3 030 000 |
| константан | 2 000 000 |
| манганин | 2 330 000 |
| ртуть | 1 040 000 |
| нихром | 893 000 |
| графит | 125 000 |
| вода морская | 3 |
| земля влажная | 10 −2 |
| вода дистилл. | 10 −4 |
| мрамор | 10 −8 |
| Сжиженные углеводородные газы | 1.2*10 −10 |
| стекло | 10 −11 |
| фарфор | 10 −14 |
| кварцевое стекло | 10 −16 |
| янтарь | 10 −18 |
Источник данных: Кухлинг Х. Справочник по физике. Пер. с нем., М.: Мир, 1982, стр. 475 (табл. 39); значения удельной проводимости вычислены из удельного сопротивления и округлены до 3 значащих цифр.
Электропроводность веществ
Примечания
Электропроводность и носители тока
Электропроводность всех веществ связана с наличием в них носителей тока (носителей заряда) — подвижных заряженных частиц (электронов, ионов) или квазичастиц (например, дырок в полупроводнике), способных перемещаться в данном веществе на большое расстояние, упрощенно можно сказать, что имеется в виду что такая частица или квазичастица должна быть способна пройти в данном веществе сколь угодно большое, по крайней мере макроскопическое, расстояние, хотя в некоторых частных случаях носители могут меняться, рождаясь и уничтожаясь (вообще говоря, иногда, возможно, и через очень небольшое расстояние), и переносить ток, сменяя друг друга.
Поскольку плотность тока определяется формулой
j→=qnv→cp.<\displaystyle <\vec
j→=∑iqiniv→icp.<\displaystyle <\vec
то, учитывая, что (установившаяся) средняя скорость каждого типа частиц при движении в конкретном веществе (среде) пропорциональна приложенному электрическому полю (в том случае, когда движение вызвано именно этим полем, что мы здесь и рассматриваем):
где μ — коэффициент пропорциональности, называемый подвижностью и зависящий от вида носителя тока в данной конкретной среде,
видим, что для электропроводности справедливо:
σ=∑iqiniμi<\displaystyle \sigma =\sum _q_n_\mu _> для более чем одного вида носителей.
Удельная электропроводность[править | править код]
Удельной электропроводностью (удельной проводимостью) называют меру способности вещества проводить электрический ток. Согласно закону Ома в линейном изотропном веществе удельная проводимость является коэффициентом пропорциональности между плотностью возникающего тока и величиной электрического поля в среде:
σ <\displaystyle \sigma >— удельная проводимость, J→<\displaystyle <\vec
Электрическая проводимость G однородного проводника длиной L с постоянным поперечным сечением площадью S может быть выражена через удельную проводимость вещества, из которого сделан проводник:
В системе СИ удельная электропроводность измеряется в сименсах на метр (См/м) или в Ом−1·м−1. В СГСЭ единицей удельной электропроводности является обратная секунда (с−1).









В неоднородной среде σ может зависеть (и в общем случае зависит) от координат, то есть не совпадает в различных точках проводника.
Удельная проводимость анизотропных (в отличие от изотропных) сред является, вообще говоря, не скаляром, а тензором (симметричным тензором ранга 2), и умножение на него сводится к матричному умножению:
при этом векторы плотности тока и напряжённости поля в общем случае не коллинеарны.
Для любой линейной среды можно выбрать локально (а если среда однородная, то и глобально) т. н. собственный базис — ортогональную систему декартовых координат, в которых матрица σik<\displaystyle \sigma _
Величины σi<\displaystyle \sigma _> называют главными значениями тензора удельной проводимости. В общем случае приведённое соотношение выполняется только в одной системе координат.
Величина, обратная удельной проводимости, называется удельным сопротивлением.
Вообще говоря, линейное соотношение, написанное выше (как скалярное, так и тензорное), верно в лучшем случае приближённо, причём приближение это хорошо только для сравнительно малых величин E. Впрочем, и при таких величинах E, когда отклонения от линейности заметны, удельная электропроводность может сохранять свою роль в качестве коэффициента при линейном члене разложения, тогда как другие, старшие, члены разложения дадут поправки, обеспечивающие хорошую точность.









Также в случае нелинейной зависимости J от E (то есть в общем случае) может явно вводиться дифференциальная удельная электропроводность, зависящая от E:
Электропроводность растворов
Скорость движения ионов зависит от напряженности электрического поля, температуры, вязкости раствора, радиуса и заряда иона и межионного взаимодействия.
У растворов сильных электролитов наблюдается характер концентрационной зависимости электрической проводимости объясняется действием двух взаимнопротивоположных эффектов. С одной стороны, с ростом разбавления уменьшается число ионов в единице объёма раствора. С другой стороны, возрастает их скорость за счет ослабления торможения ионами противоположного знака.
Для растворов слабых электролитов наблюдается характер концентрационной зависимости электрической проводимости можно объяснить тем, что рост разбавления ведёт, с одной стороны, к уменьшению концентрации молекул электролита. В то же время возрастает число ионов за счёт роста степени ионизации.
В отличие от металлов (проводники 1-го рода) электрическая проводимость растворов как слабых, так и сильных электролитов (проводники 2-го рода) при повышении температуры возрастает. Этот факт можно объяснить увеличением подвижности в результате понижения вязкости раствора и ослаблением межионного взаимодействия
Электрофоретический эффект — возникновение торможения носителей вследствие того, что ионы противоположного знака под действием электрического поля двигаются в направлении, обратном направлению движения рассматриваемого иона
Релаксационый эффект — торможение носителей в связи с тем, что ионы при движении расположены асимметрично по отношению к их ионным атмосферам. Накопление зарядов противоположного знака в пространстве за ионом приводит к торможению его движения.









При больших напряжениях электрического поля скорость движения ионов настолько велика, что ионная атмосфера не успевает образоваться. В результате электрофоретическое и релаксационное торможение не проявляется.
Электропроводность металлов[править | править код]
Ещё до открытия электронов было обнаружено, что протекание тока в металлах, в отличие от тока в жидких электролитах, не обусловлено переносом вещества металла. Эксперимент, который выполнил немецкий физик Карл Виктор Эдуард Рикке (Riecke Carl Viktor Eduard) в 1901 году, состоял в том, что через контакты различных металлов, — двух медных и одного алюминиевого цилиндра с тщательно отшлифованными торцами, поставленными один на другой, в течение года пропускался постоянный электрический ток. Затем исследовался состав материала вблизи контактов. Оказалось, что переноса вещества металла через границу не происходит и вещество по разные стороны границы раздела имеет тот же состав, что и до пропускания тока. Таким образом было показано, что перенос электрического тока осуществляется не атомами и молекулами металлов. Однако эти опыты не дали ответа на вопрос о природе носителей заряда в металлах.
Связь с коэффициентом теплопроводностиправить | править код
Основная статья: Закон Видемана — Франца
Закон Видемана — Франца, выполняющийся для металлов при высоких температурах, устанавливает однозначную связь удельной электрической проводимости σ <\displaystyle \sigma >с коэффициентом теплопроводности K:
где k — постоянная Больцмана, e — элементарный заряд. Эта связь основана на том факте, что как электропроводность, так и теплопроводность в металлах обусловлены движением свободных электронов проводимости.
СОДЕРЖАНИЕ
Единицы
СИ единицей проводимости является S / м и, если иное квалификацию, он не относится к 25 ° C. Чаще встречается традиционная единица измерения мкСм / см.
Преобразование проводимости в общее количество растворенных твердых веществ зависит от химического состава образца и может варьироваться от 0,54 до 0,96. Как правило, преобразование выполняется, предполагая, что твердым веществом является хлорид натрия, т.е. 1 мкСм / см в этом случае эквивалентно примерно 0,64 мг NaCl на кг воды.
Измерение
На рынке имеется широкий выбор приборов. Чаще всего используются два типа электродных датчиков: электродные датчики и индукционные датчики. Электродные датчики со статической конструкцией подходят для низкой и средней проводимости и существуют в различных типах, с 2 или 4 электродами, где электроды могут быть расположены напротив друг друга, плоские или в цилиндре. Электродные ячейки с гибкой конструкцией, в которой расстояние между двумя противоположно расположенными электродами может варьироваться, обеспечивают высокую точность и также могут использоваться для измерения высокопроводящих сред. Индуктивные датчики подходят для жестких химических условий, но требуют большего объема пробы, чем электродные датчики. Датчики проводимости обычно калибруются растворами KCl известной проводимости. Электролитическая проводимость сильно зависит от температуры, но многие коммерческие системы предлагают автоматическую температурную коррекцию. Таблицы эталонных проводимостей доступны для многих распространенных решений.
Определения
Сопротивление R пропорционально расстоянию l между электродами и обратно пропорционально площади поперечного сечения образца A ( обозначено буквой S на рисунке выше). Записывая ρ (rho) для удельного сопротивления (или удельного сопротивления ),
Удельная проводимость (проводимость) κ (каппа) обратно пропорциональна удельному сопротивлению.
Теория
Сильные электролиты
Сильные электролиты предположили диссоциируют полностью в растворе. Электропроводность раствора сильного электролита при низкой концентрации подчиняется закону Кольрауша.
Однако по мере увеличения концентрации проводимость больше не увеличивается пропорционально. Более того, Кольрауш также обнаружил, что предельная проводимость электролита;
В следующей таблице приведены значения предельной молярной проводимости для некоторых выбранных ионов.
Интерпретация этих результатов была основана на теории Дебая и Хюккеля, что привело к теории Дебая-Хюккеля-Онзагера:
Слабые электролиты
Различные растворители демонстрируют одинаковую диссоциацию, если отношение относительных диэлектрических проницаемостей равно отношению кубических корней концентраций электролитов (правило Вальдена).
Более высокие концентрации
Существование так называемого минимума проводимости в растворителях с относительной диэлектрической проницаемостью ниже 60 оказалось спорным вопросом с точки зрения интерпретации. Фуосс и Краус предположили, что это вызвано образованием ионных триплетов, и это предположение недавно получило некоторую поддержку.
Системы смешанных растворителей
Проводимость в зависимости от температуры
Обычно проводимость раствора увеличивается с повышением температуры, так как подвижность ионов увеличивается. Для сравнения эталонные значения указаны при согласованной температуре, обычно 298 K (≈ 25 ° C или 77 ° F), хотя иногда используется 20 ° C (68 ° F). Так называемые «компенсированные» измерения выполняются при удобной температуре, но сообщаемое значение является расчетным значением ожидаемого значения проводимости раствора, как если бы оно было измерено при эталонной температуре. Базовая компенсация обычно выполняется, исходя из предположения, что линейное увеличение проводимости в зависимости от температуры обычно составляет 2% на Кельвин. Это значение широко применимо для большинства солей при комнатной температуре. Определить точный температурный коэффициент для конкретного раствора просто, и приборы, как правило, могут применять производный коэффициент (т.е. отличный от 2%).
Изотопный эффект растворителя
Изменение проводимости из-за изотопного эффекта для дейтерированных электролитов является значительным.
Приложения
Несмотря на сложность теоретической интерпретации, измеренная проводимость является хорошим индикатором присутствия или отсутствия проводящих ионов в растворе, и измерения широко используются во многих отраслях промышленности. Например, измерения электропроводности используются для контроля качества воды в коммунальном водоснабжении, больницах, котловой воде и в промышленности, которая зависит от качества воды, например, в пивоварении. Этот тип измерения не зависит от ионов; иногда его можно использовать для определения общего количества растворенных твердых веществ (TDS или TDS), если известны состав раствора и его поведение проводимости. Измерения проводимости, проводимые для определения чистоты воды, не будут реагировать на непроводящие загрязнения (многие органические соединения попадают в эту категорию), поэтому в зависимости от области применения могут потребоваться дополнительные испытания на чистоту.
Иногда измерения проводимости связаны с другими методами, чтобы повысить чувствительность обнаружения определенных типов ионов. Например, в технологии котловой воды продувка котла постоянно контролируется на предмет «катионной проводимости», то есть проводимости воды после того, как она прошла через катионообменную смолу. Это чувствительный метод контроля анионных примесей в котловой воде в присутствии избытка катионов (в составе подщелачивающего агента, обычно используемого для обработки воды). Чувствительность этого метода зависит от высокой подвижности H + по сравнению с подвижностью других катионов или анионов. Помимо катионной проводимости, существуют аналитические приборы, предназначенные для измерения проводимости по дегазации, где проводимость измеряется после удаления растворенного диоксида углерода из образца путем повторного кипячения или динамической дегазации.
Как же измеряется содержание солей в жидкости? Раньше приходилось выпаривать воду в ёмкости, остаток солей принимать за ориентир. Сегодня достаточно погрузить прибор в воду и в считанные секунды мы уже в курсе сколько ppm содержит жидкость, но об этом чуть позднее.
Растения требуют определенного уровня TDS, определенный период питания растений характеризуется определенной программой: вегетативное развитие, цветение и получение плодов. В качестве единицы уровня насыщенности минералами принято считать миллиграмм на литр, что означает массу соли растворенную в одном литре воды.
Иногда уровень минерализации определяется зависимостью частиц соли на миллион частиц воды. Сокращенно: ppm (parts per million).
Удельная электропроводность
Электропроводность часто называют кондуктометрией – электрохимический метод исследований, который основан на измерении электропроводности растворов. От того, насколько проводит ток вещество, зависит морфология растения. Это очень важно при сборе конечного урожая (качества и количества). Кондуктометр и есть прибор, которым измеряют проводимость растворов. Большинство современных устройств имеют показатели таких значений, как EC и ppm.
Интересно, что дистиллированная вода не проводит электричество. Она имеет бесконечный запас электропроводности. Как только соли попадают в воду, через нее начинает проходить ток. Чем больше соли будет в воде, тем больше проводимость у жидкости.
Соли имеют различную электропроводность. Чем выше проводимость воды, тем выше должна быть концентрация солей. Соленую воду растениям поглощать сложнее. С помощью специальных приборов можно быстро измерить удельную проводимость воды. Сегодня существует большое количество способов проверить состав воды любого происхождения.
Стоимость TDS-метра бывает разной. Все зависит от его оснащения. Несмотря на цену, прибор очень чувствителен к механическим повреждениям. Потому очень важно обращаться с прибором аккуратно. Перед использованием оборудования прочтите инструкцию и откалибруйте.
Единицы измерения ЕС
Основной единицей сопротивления является Ом. Удельная проводимость, как известно, величина, обратная сопротивлению. Ее измеряют в Сименсах.
Разница между TDS, PPM, EC сложнее чем может показаться. Одна измерительная базовая основа в различных системах показывает разные данные. Основной считается EC, но например большинство производителей Америки применяют PPM, в европе же своя история. Производители используют различные стандартные значения преобразования между PPM, EC, CF. В системе гидропоники чаще всего применяются шкалы:
Итак, ppm: 1000 Ppm = 1 Ppt (Частей на триллион).
Далее EC: 1000 µS (Микросименс/см) = 1 mS (Миллисименс/см).
Итог: 1 µS (Микросименс/см) = 1 EC = 10 CF.
Остается добавить, что карманные TDS-метры используют шкалу 500, и если производитель дает рекомендации в ЕС, по этой таблице легко получить РРМ
Электрическая проводимость
 Классическая электродинамика Классическая электродинамика | ||||||||||||
 | ||||||||||||
| Электричество · Магнетизм | ||||||||||||
| ||||||||||||
| См. также: Портал:Физика |
Содержание
Удельная проводимость
Удельной проводимостью (удельной электропроводностью) называют меру способности вещества проводить электрический ток. Согласно закону Ома в линейном изотропном веществе удельная проводимость является коэффициентом пропорциональности между плотностью возникающего тока и величиной электрического поля в среде:
В неоднородной среде σ может зависеть (и в общем случае зависит) от координат, то есть не совпадает в различных точках проводника.
Удельная проводимость анизотропных (в отличие от изотропных) сред является, вообще говоря, не скаляром, а тензором (симметричным тензором ранга 2), и умножение на него сводится к матричному умножению:
векторы же плотности тока и напряжённости поля в этом случае, вообще говоря, не коллинеарны.
Для любой линейной среды можно выбрать локально (а если среда однородная, то и глобально) ортогональную систему координат (собственные оси тензора проводимости), в которой тензор проводимости диагонализуется. В таких координатах соотношение упрощается и записывается так:
(но такое соотношение для анизотропной среды реализуется только в одних выделенных координатах) [2]
Величина, обратная удельной проводимости, называется удельным сопротивлением.
Электрическая проводимость G проводника длиной L с площадью поперечного сечения S может быть выражена через удельную проводимость вещества, из которого сделан проводник, следующей формулой:
Связь с коэффициентом теплопроводности
Закон Видемана — Франца устанавливает однозначную связь удельной электрической проводимости 

Электропроводность металлов
Ещё задолго до открытия электронов было экспериментально показано, что прохождение тока в металлах не связано, в отличие от тока в жидких электролитах, с переносом вещества металла. Опыт состоял в том, что через контакт двух различных металлов, например золота и серебра, в течение времени, исчисляемого многими месяцами, пропускался постоянный электрический ток. После этого исследовался материал вблизи контактов. Было показано, что никакого переноса вещества через границу не наблюдается и вещество по различные стороны границы раздела имеет тот же состав, что и до пропускания тока. Эти опыты показали, что атомы и молекулы металлов не принимают участия в переносе электрического тока, но они не ответили на вопрос о природе носителей заряда в металлах.
Опыты Толмена и Стюарта
Прямым доказательством, что электрический ток в металлах обуславливается движением электронов, были опыты Толмена и Стюарта, проведённые в 1916 г. Идея этих опытов была высказана Мандельштамом и Папалекси в 1913 г.
Возьмём катушку, которая может вращаться вокруг своей оси. Концы катушки с помощью скользящих контактов замкнуты на гальванометр. Если находящуюся в быстром вращении катушку резко затормозить, то свободные электроны в проволоке продолжат двигаться по инерции, в результате чего гальванометр должен зарегистрировать импульс тока.
При достаточно плотной намотке и тонких проводах можно считать, что линейное ускорение катушки при торможении 


Поэтому эффективная электродвижущая сила в катушке, обусловленная инерцией свободных электронов, равна
где L — длина провода на катушке. [4]
Введём обозначения: I — сила тока, протекающего по замкнутой цепи, R — сопротивление всей цепи, включая сопротивление проводов катушки и проводов внешней цепи и гальванометра. Запишем закон Ома в виде:
Тогда за время торможения через гальванометр пройдёт заряд
Удельная проводимость некоторых веществ
Удельная проводимость приведена при температуре 20 °C [5] :