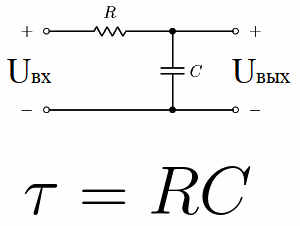в чем измеряется тау

Природе свойственны периодические процессы: день сменяет ночь, теплое время года сменяется холодным и т. д. Период этих событий почти постоянен и поэтому может быть строго определен. Кроме того, мы вправе утверждать, что приведенные в качестве примера периодические природные процессы не являются затухающими, по крайней мере по отношению к продолжительности жизни одного человека.

Сплошь и рядом в электротехнике можно встретить так называемые экспоненциальные переходные процессы, суть которых заключается в том, что система просто стремится придти к какому-то равновесному состоянию, которое в конце концов выглядит как состояние покоя. Такой переходный процесс может быть как нарастающим, так и спадающим.

Внешняя сила сначала выводят динамическую систему из состояния равновесия, а затем не препятствует естественному возврату данной системы к ее исходному состоянию. Эта последняя фаза и есть так называемый переходный процесс, которому свойственна определенная длительность. Кроме того процесс выведения системы из равновесия также является переходным процессом с характерной длительностью.

Так или иначе, постоянной времени переходного процесса мы называем его временную характеристику, определяющую время, через которое некоторый параметр данного процесса изменится в «е» раз, то есть увеличится или уменьшится примерно в 2,718 раз по сравнению с состоянием, принятым за исходное.

Рассмотрим для примера электрическую цепь, состоящую из источника постоянного напряжения, конденсатора и резистора. Подобного рода цепь, где резистор включен последовательно с конденсатором, называется интегрирующей RC-цепью.

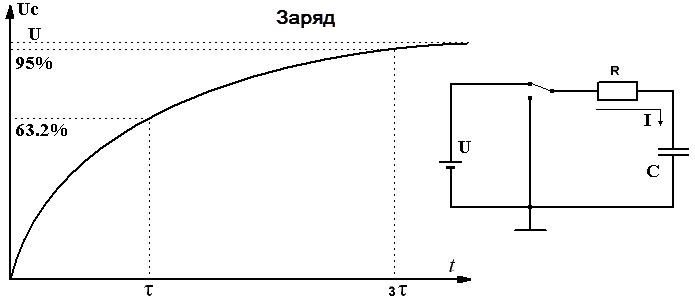
Если в начальный момент времени подать на такую цепь питание, то есть установить на входе некоторое постоянное напряжение Uвх, то Uвых — напряжение на конденсаторе, начнет по экспоненте нарастать.

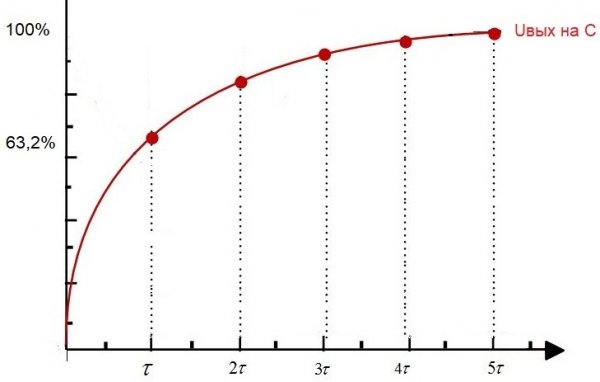
Через время t1 напряжение на конденсаторе достигнет 63,2% от напряжения на входе. Так вот, промежуток времени от начального момента до t1 – это и будет постоянная времени данной RC-цепи.

Данную константу цепи называют «тау», она измеряется в секундах, а обозначают ее соответствующей греческой буквой. Численно для RC-цепи она равна R*C, где R выражается в омах, а С — в фарадах.

Интегрирующие RC-цепи применяются в электронике в качестве фильтров нижних частот, когда более высокие частоты необходимо отсечь (подавить), а более низкие — пропустить.

Практически механизм такой фильтрации зиждиться на следующем принципе. Для переменного тока конденсатор выступает как емкостное сопротивление, значение которого обратно пропорционально частоте, то есть чем выше частота — тем меньшим будет реактивное сопротивление конденсатора в омах.

Следовательно, если пропустить через RC-цепь переменный ток, то, как на плечах делителя напряжения, на конденсаторе упадет определенное напряжение, пропорциональное его емкостному сопротивлению на частоте пропускаемого тока.

Если известна частота среза и амплитуда входного переменного сигнала, то для разработчика не составит труда подобрать такие конденсатор и резистор в RC-цепь, чтобы минимальное (граничное) напряжение (для частоты среза — верхней частотной границы) приходилось на конденсатор как на реактивное сопротивление, входящее в состав делителя в совокупности с резистором.

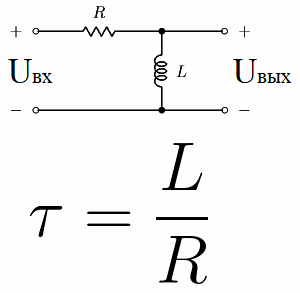
Теперь рассмотрим так называемую дифференцирующую цепь. Это цепь, состоящая из последовательно соединенных резистора и катушки индуктивности, RL-цепь. Ее постоянная времени численно равна L/R, где L – индуктивность катушки в генри, а R – сопротивление резистора в омах.

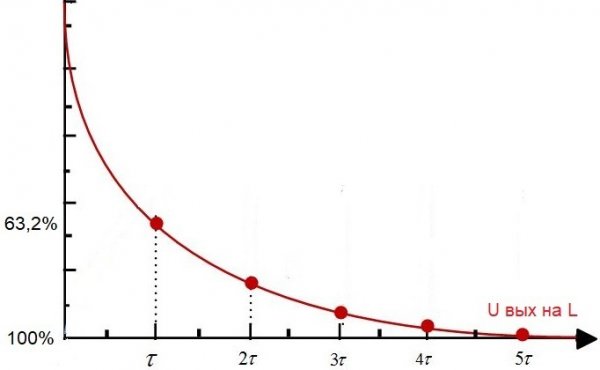
Если к такой цепи приложить постоянное напряжение от источника, то через время тау напряжение на катушке уменьшится по сравнению с U вх на 63,2%, то есть в полном соответствии со значением постоянной времени для данной электрической цепи.

В цепях переменного тока (переменных сигналов) LR-цепи применяются в качестве фильтров верхних частот, когда низкие частоты необходимо отсечь (подавить), а частоты выше (выше частоты среза — нижней частотной границы)— пропустить. Так вот, индуктивное сопротивление катушки тем больше, чем выше частота.

Как и в случае с рассмотренной выше RC-цепью, здесь используется принцип делителя напряжения. Ток более высокой частоты, пропускаемый через RL-цепь, вызовет большее падение напряжения на индуктивности L, как на индуктивном сопротивлении, входящем в состав делителя напряжения в совокупности с резистором. Задача разработчика — подобрать такие R и L, чтобы минимальное (граничное) напряжение на катушке получалось как раз на частоте среза.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Источник

Постоянная времени цепи RC

Электрическая цепь RC

Из рисунка видно, что электрический ток I в элементах C и R цепи будет иметь одинаковое значение и противоположное направление, согласно закону Кирхгофа. Следовательно, его можно выразить следующим образом:

Интегрируем:

Из таблицы интегралов здесь используем преобразование

Постоянная времени τ

Если конденсатор емкостью C последовательно с резистором сопротивлением R подключить к источнику постоянного напряжения U, в цепи пойдёт ток, который за любое время t зарядит конденсатор до значения U_C и определится выражением:

Тогда напряжение U_C на выводах конденсатора будет увеличиваться от нуля до значения U по экспоненте:

Постоянная времени τ = RC

Если к конденсатору емкостью C, заряженному до напряжения U, параллельно подключить резистор сопротивлением R, тогда в цепи пойдёт ток разряда конденсатора.

За время τ напряжение на конденсаторе уменьшится до значения U/e, что составит 1/e*100% ≈ 36.8% значения U.
За время 3τ конденсатор разрядится до (1/e 3 )*100% ≈ 5% от значения U.
За время 5τ до (1/e 5 )*100% ≈ 1% значения U.

Параметр τ широко применяется при расчётах RC-фильтров различных электронных цепей и узлов.

Замечания и предложения принимаются и приветствуются!

Источник

ПОМОГИТЕ РАЗОБРАТЬСЯ. Механика. Подробно объясните что такое касательное напряжение (тау)

Напряжение в точке тела в разных направлениях (на разных площадках, проходящих через данную точку тела) может быть различным (в частности, оно может возникать только в одном направлении).

Понятие о напряжении в точке деформируемого твердого тела ввел в 1822 г. французский ученый Огюстен Луи Коши.

Основную роль в расчетах прочности играет не полное напряжение p, а его проекции на оси координат x, y и z: нормальное напряжение (изображение Напряжение сопромат – сигма), направленное по перпендикуляру к площадке (параллельно оси z), и касательные напряжения (изображение Напряжение сопромат – тау), лежащие в плоскости сечения и направленные, соответственно, вдоль осей x и y (рис. 1.4, б). Первый индекс у касательных напряжений характеризует нормаль к площадке z, на которой они возникают.

Между полным (изображение Напряжение сопромат), нормальным (изображение Напряжение сопромат) и касательными напряжениями (изображение Напряжение сопромат и изображение Напряжение сопромат) существует зависимость:

изображение Напряжение сопромат.

Касательные напряжения служат мерой тенденции одной части сечения смещаться (или скользить) относительно другой его части.

Единицы нормальных и касательных напряжений в СИ – паскаль (Па). Один паскаль – это напряжение, при котором на площадке в один квадратный метр возникает внутренняя сила, равная одному ньютону (то есть равная, приблизительно, весу одного яблока). Как мы увидим в дальнейшем, эта единица напряжения мизерно мала. В сопромате чаще используются другие единицы:

1 МПа = 106 Па; 1 кН/см2 = 107 Па.

Источник

Время на квантовом уровне течет иначе. Но как? И что это означает для физики?

До начала ХХ столетия считалось, что время – есть величина абсолютная. Но после того, как Альберт Эйнштейн опубликовал общую теорию относительности (ОТО), стало понятно, что время – понятие более субъективное и имеет отношение к наблюдателю, который его измеряет. И все же, многие продолжали трактовать время так, словно это прямая железнодорожная линия, двигаться по которой можно только вперед или назад. Но что, если эта железнодорожная линия ветвится или вовсе имеет окружные пути, двигаясь по которым поезд возвращается на станцию, которую уже проезжал? Иными словами, можно ли путешествовать в будущее или прошлое? Начиная со знаменитого романа Герберта Уэллса «Машина времени», научные фантасты придаются фантазиям во всю. Но в реальной жизни представить нечто подобное невозможно. Ведь если бы кто-то в будущем изобрел машину времени, неужто он бы не предупредил нас об угрозе пандемии COVID-19 или об ужасных последствиях глобального потепления? Но к нам так никто и не прибыл. Быть может, стоит посмотреть на время под другим углом?

Законы квантового мира очень сильно отличаются от тех, что мы можем непосредственно наблюдать

Квантовая механика – раздел теоретической физики, описывающий физические явления, действие в которых сравнимо по величине с постоянной Планка.

Ход времени

Наше понятие времени восходит к картине, описанной Исааком Ньютоном: стрела времени движется только вперед, лишая нас всякой возможности вернуться назад, в прошлое. В то же самое время ОТО гласит, что ход времени различен для наблюдателей в разных гравитационных полях.

Это означает, что у поверхности Земли время течет медленнее, так как сила гравитации на планете сильнее, чем на орбите. И чем сильнее гравитационное поле, тем больше этот эффект. Подробнее о том, почему время на вершине горы и на пляже течет по-разному, можно прочитать здесь.

Выходит, законы движения Ньютона положили конец идее абсолютного положения времени в пространстве, а теория относительности и вовсе поставила на этой идее крест. Более того, как пишут в своей книге «Кратчайшая история времени» физики Стивен Хокинг и Леонард Млодинов, путешествия во времени возможны.

Обложка замечательной книги Стивена Хокинга и Леонарда Млодинова, настоятельно рекомендуем к прочтению

Теория относительности показывает, что создание машины времени, способной переместить нас в будущее действительно возможно. Все, что нужно сделать после ее создания – войти внутрь, подождать некоторое время, а затем выйти – и обнаружить, что на Земле время шло иначе, нежели для вас. То есть намного быстрее. Безусловно, никто на планете не обладает подобными технологиями, но их появление – вопрос времени. Ведь если хорошенько подумать, то что нужно для изобретения такой машины?

Во-первых, она должна разгонятся до околосветовых скоростей (напомню, что скорость света достигает 300 000 км/с), а во-вторых, следует вспомнить знаменитый парадокс близнецов, при помощи которого физики пытаются доказать противоречивость специальной теории относительности, которая гласит, что с точки зрения «неподвижных» наблюдателей все процессы у двигающихся объектов замедляются.

Согласно специальной теории относительности (СТО) все физические законы одинаковы для всех свободно двигающихся наблюдателей, независимо от их скорости.

Альберт Эйнштейн опубликовал теорию относительности 106 лет назад.

Немного проясним – данный способ предполагает, что машина времени, в которую вы вошли, взлетает, разгоняется до околосветовой скорости, движется так какое-то время (в зависимости от того, как далеко вперед во времени вы направляетесь) и затем возвращается назад. Когда путешествие заканчивается, покинув машину времени вы понимаете, что для вас прошло намного меньше времени, чем для всех жителей Земли – вы совершили путешествие в будущее. Но если отныне мы воспринимаем время по-другому, быть может, законы физики подскажут, как путешествовать в прошлое?

Можно ли отправиться в прошлое?

Первый намек на то, что человек может совершать путешествия во времени, появился в 1949 году, когда австрийский математик Курт Гедель нашел новое решение уравнений Эйнштейна. Или новую структуру пространства-времени, допустимую с точки зрения ОТО.

Вообще, говоря об уравнениях Эйнштейна, важно понимать, что они удовлетворяют множество разных математических моделей Вселенной. Эти модели различаются, например, начальными или граничными условиями.

И чтобы понять, соответствуют ли они Вселенной, в которой мы живем, мы должны проверить их физические предсказания.

Кстати, если вы давно не пересматривали «Назад в будущее» – самое время)

Гедель, будучи математиком, прославился тем, что доказал – не все истинные утверждения можно доказать, даже если дело сводится к попытке доказать все истинные утверждения, например, с помощью простой арифметики. Таким образом, подобно принципу неопределенности, теорема Геделя о неполноте может быть фундаментальным ограничением нашей способности познавать и предсказывать Вселенную.

Принцип неопределенности – принцип, сформулированный Гейзенбергом и утверждающий, что нельзя одновременно точно определить и положение, и скорость частицы; чем точнее мы знаем одно, тем менее точно другое.

Интересно, что пространство-время Геделя имело любопытную особенность: Вселенная в его представлении вращалась как целое. А вот Эйнштейн был очень огорчен тем, что его уравнения допускают подобное решение. Общая теория относительности в его понимании не должна позволять путешествия во времени. Уравнение Геделя, однако, не соответствует Вселенной, в которой мы живем, но его труд позволил миру взглянуть на время (а заодно и на Вселенную) иначе.

Итак, пространство-время, как известно, тесно взаимосвязаны. Это означает, что вопрос о путешествиях во времени переплетается с проблемой перемещения на скоростях, превыщающих 300 000 км/с, то есть скорость света. А когда речь заходит о фотонах, общая теория относительности, увы, уходит на задний план, а ее место занимает квантовая механика.

Подробнее о том, что изучает квантовая механика, а главное как, мы рассказывали в этой статье, рекомендую к прочтению!

Переход на квантовый уровень

Не так давно команда физиков из Университетов Вены, Бристоля, Балеарских островов и Института квантовой оптики и квантовой информации (IQOQI-Вена) показала, как квантовые системы могут одновременно развиваться по двум противоположным временным стрелкам (вперед и назад во времени). Иными словами, квантовые системы могут двигаться как вперед, так и назад во времени.

Квантовые системы могут двигаться как вперед, так и назад во времени

Ранее, чтобы понять почему, ученые установили, что время знает только одно направление — вперед. Так что нам с вами придется вспомнить второй закон термодинамики. Он гласит, что в замкнутой системе энтропия системы (то есть мера беспорядка и случайности внутри системы) остается постоянной или увеличивается.

Если наша Вселенная представляет собой замкнутый цикл, свернутый в клубок, ее энтропия никогда не может уменьшиться, а это означает, что Вселенная никогда не вернется в более раннюю точку. Но что, если бы стрела времени «посмотрела» на явления, где изменения энтропии невелики?

Второй закон термодинамики – это статистический закон, в среднем верный для макроскопической системы. В микроскопической системе мы можем видеть, как система естественным образом эволюционируют в сторону ситуаций с более низкой энтропией, – пишут авторы научной работы.

Вот что говорит об этом Джулия Рубино, научный сотрудник Университета Бристоля и ведущий автор новой статьи: «Давайте предположим, что в начале газ в сосуде занимает только его половину. Затем представьте, что мы удаляем клапан, который удерживал его в пределах половины сосуда, так что газ теперь может свободно расширяться по всему сосуду».

Термодинамика хранит в себе множество тайн о нашем мире и Вселенной

В результате мы увидим, что частицы начнут свободно перемещаться по всему объему сосуда. Со временем газ займет весь сосуд. «В принципе, существует ненулевая вероятность того, что в какой-то момент газ естественным образом вернется, чтобы занять половину сосуда, только эта вероятность становится меньше, чем больше становится количество частиц, составляющих газ», – объясняет Рубино.

Если бы существовало только три частицы газа вместо огромного количества газа (состоящего из миллиардов частиц), эти несколько частиц могли бы снова оказаться в той части сосуда, откуда они первоначально стартовали. Вот такая физика.

ОТО допускает путешествия во времени в будущее. С прошлым все намного сложнее

Далее, как вы могли догадаться, следует второй закон термодинамики – так называемый статистический закон, который является верным в среднем для макроскопической системы. «В микроскопической системе мы можем видеть, как система естественным образом эволюционирует в сторону ситуаций с более низкой энтропией», – отмечают исследователи.

Стрела времени

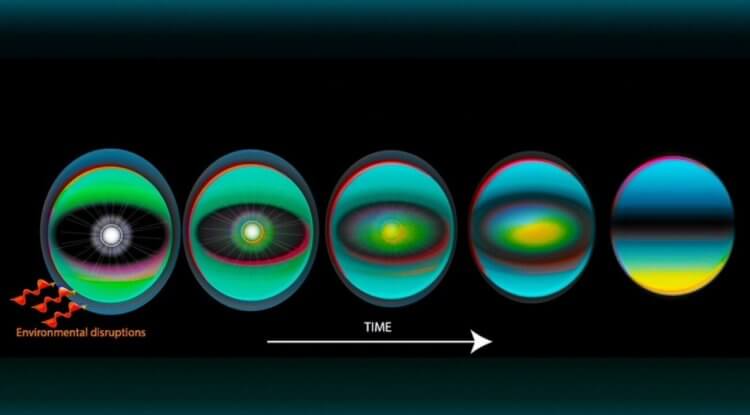
Чтобы разобраться еще подробнее, отметим, что в ходе нового исследования физики задавались вопросом о последствиях применения описанной выше парадигмы в квантовой области. Согласно принципу квантовой суперпозиции, отдельные единицы (например, свет) могут существовать одновременно в двух состояниях, как в виде волн, так и в виде частиц, проявляясь в том или ином виде в зависимости от того, что именно вы тестируете.

Команда Рубино рассмотрела квантовую суперпозицию с состоянием, которое развивается как назад, так и вперед во времени. Измерения показали, что чаще всего система в конечном итоге движется вперед во времени. Если бы не небольшие изменения энтропии, система действительно могла бы продолжать развиваться как вперед, так и назад во времени.

Разрушение суперпозиции состоянии при взаимодействии с окружением с течением времени Изображение Joint Quantum Institute

Так как же эти сложные физические понятия соотносятся с реальным человеческим опытом? Неужели наконец-то пришло время начать собирать вещи для путешествия назад во времени? Увы.

«Мы, люди, являемся макроскопическими системами. Мы не можем воспринимать эти квантовые суперпозиции временных эволюций», – говорит Рубино. Для нас время действительно движется вперед. Возможно, это тот случай, когда мир немного не определился.

И действительно – на самом фундаментальном уровне мир состоит из квантовых систем (которые могут двигаться вперед и назад). Более глубокое понимание того, как описать течение времени на уровне этих элементарных составляющих, могло бы позволить физикам сформулировать более точные теории для их описания и, в конечном счете, получить более глубокое понимание физических явлений мира, в котором мы живем.

Еще больше интересных статей обо всем на свете, а также о путешествиях во времени и Мультивселенной читайте на нашем канале в Яндекс.Дзен. Там регулярно выходят статьи, которых нет на сайте!

Выводы

Однако не все согласны с тем, что различие между макроскопическим и микроскопическим является четким. Как пишет Popular Mechanics, Рамакришна Подила, доцент кафедры физики и астрономии Университета Клемсона в Южной Каролине, говорит, что статистика многих частиц по сравнению со статистикой отдельных частиц является более точным способом описания вещей.

Даже у одной частицы есть свои собственные, уникальные микросостояния. Подила считает, что в нашем стремлении понять время мы ставим уравнения выше физической реальности — и упускаем главное.

Связывание стрелы времени с энтропией или коллапсом квантово-механической системы (как указано в статье) – это не формальные утверждения, а популярные методы, которые просты в использовании. Даже то, что время движется вперед, само по себе не аксиома, а теория, которую астрофизик Артур Эддингтон придумал и популяризировал в 1927 году.

Время и пространство неразрывно связаны, но правильно ли мы их понимаем?

Так что, возможно, идея о том, что пространство и время сливаются в один переплетенный континуум, имеет право на жизнь. С тех пор как Альберт Эйнштейн сформулировал теорию относительности, мы перестали воспринимать пространство как трехмерную фигуру, а время — как одномерное.

Время стало четвертым элементом четырехмерного вектора, описывающего пространство и время, — говорит Рубино. Это единая, динамичная сущность, над которой мы все еще ломаем голову.

В заключение же хочу не только поблагодарить читателя за внимание, но и вновь процитировать ученых: «Хотя время часто рассматривается как непрерывно увеличивающийся параметр, наше исследование показывает, что законы, управляющие его течением в квантово-механических контекстах, намного сложнее. Это может означать, что нам нужно переосмыслить то, как мы представляем эту величину во всех тех контекстах, где квантовые законы играют решающую роль».

Из-за квантовой суперпозиции ход времени в микромире не имеет определенного направления — исчезает грань между причиной и следствием.

Полностью ознакомиться с текстом научной работы можно в журнале Nature. Кстати, как вы думаете, можно ли путешествовать во времени и что новое исследование говорит нам о Вселенной? Ответ будем ждать здесь, а также в комментариях к этой статье!

Новости, статьи и анонсы публикаций

Свободное общение и обсуждение материалов

Физикам впервые удалось не только создать максимально правдоподобный кристалл Вигнера, но даже изучить его свойства. Более того, собранные учеными визуальные данные являются наиболее убедительным доказательством существования этих удивительных объектов 🔮

Считается, что в таинственном Бермудском треугольнике каждый год пропадает по меньшей мере 20 кораблей и 4 самолета. Но ведь это очень много, быть может, тут что-то не так? Разбираемся, что современной науке известно об этом регионе и откуда вообще взялся миф о Бермудском треугольнике.

В феврале 2012 года нобелевский лауреат, физик Франк Вилчек, решил выйти на публику со странным и, как ему показалось, слегка неуклюжим предположением. Невоз…

Источник

Введение в теорию автоматического управления. Основные понятия теории управления техническим системами

Публикую первую главу лекций по теории автоматического управления, после которых ваша жизнь уже никогда не будет прежней.

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика привествуется.

1. Основные понятия теории управления техническими системами

1.1. Цели, принципы управления, виды систем управления, основные определения, примеры

Развитие и совершенствование промышленного производства (энергетики, транспорта, машиностроения, космической техники и т.д.) требует непрерывного увеличения производительности машин и агрегатов, повышения качества продукции, снижения себестоимости и, особенно в атомной энергетике, резкого повышения безопасности (ядерной, радиационной и т.д.) эксплуатации АЭС и ядерных установок.

Реализация поставленных целей невозможна без внедрения современных систем управления, включая как автоматизированные (с участием человека-оператора), так и автоматические (без участия человека-оператора) системы управления (СУ).

Определение: Управление – это такая организация того или иного технологического процесса, которая обеспечивает достижение поставленной цели.

Теория управления является разделом современной науки и техники. Она базируется (основывается) как на фундаментальных (общенаучных) дисциплинах (например, математика, физика, химия и т.д.), так и на прикладных дисциплинах (электроника, микропроцессорная техника, программирование и т.д.).

Любой процесс управления (автоматического) состоит из следующих основных этапов (элементов):

Для реализации Процесса Управления система управления (СУ) должна иметь:

Определение: Если система управления (СУ) содержит все перечисленные выше части, то она является замкнутой.

Определение: Управление техническим объектом с использованием информации о результатах управления называется принципом обратной связи.

Схематично такая система управления может быть представлена в виде:

Рис. 1.1.1 — Структура системы управления (СУ)

Если система управления (СУ) имеет структурную схему, вид которой соответствует рис. 1.1.1, и функционирует (работает) без участия человека (оператора), то она называется системой автоматического управления (САУ).

Если СУ функционирует с участием человека (оператора), то она называется автоматизированной СУ.

Если Управление обеспечивает заданный закон изменения объекта во времени независимо от результатов управления, то такое управление совершается по разомкнутому циклу, а само управление называется программным управлением.

К системам, работающим по разомкнутому циклу, относятся промышленные автоматы (конвейерные линии, роторные линии и т.д.), станки с числовым программным управлением (ЧПУ): см. пример на рис. 1.1.2.

Задающее устройство может быть, например, и “копиром”.

Поскольку в данном примере нет датчиков (измерителей), контролирующих изготавливаемую деталь, то если, например, резец был установлен неправильно или сломался, то поставленная цель (изготовление детали) не может быть достигнута (реализована). Обычно в системах подобного типа необходим выходной контроль, который будет только фиксировать отклонение размеров и формы детали от желаемой.

Автоматические системы управления подразделяются на 3 типа:

САР и СС являются подмножествами САУ ==> .

Определение: Автоматическая система управления, обеспечивающая постоянство какой-либо физической величины (группы величин) в объекте управления называется системой автоматического регулирования (САР).

Системы автоматического регулирования (САР) — наиболее распространенный тип систем автоматического управления.

Первый в мире автоматический регулятор (18-е столетие) – регулятор Уатта. Данная схема (см. рис. 1.1.3) реализована Уаттом в Англии для поддержания постоянной скорости вращения колеса паровой машины и, соответственно, для поддержания постоянства скорости вращения (движения) шкива (ремня) трансмиссии.

В данной схеме чувствительными элементами (измерительными датчиками) являются “грузы” (сферы). «Грузы» (сферы) также “заставляют” перемещаться коромысло и затем задвижку. Поэтому данную систему можно отнести к системе прямого регулирования, а регулятор — к регулятору прямого действия, так как он одновременно выполняет функции и “измерителя” и “регулятора”.

В регуляторах прямого действия дополнительного источника энергии для перемещения регулирующего органа не требуется.

В системах непрямого регулирования необходимо присутствие (наличие) усилителя (например, мощности), дополнительного исполнительного механизма, содержащего, например, электродвигатель, серводвигатель, гидропривод и т.д.

Примером САУ (системы автоматического управления), в полном смысле этого определения, может служить система управления, обеспечивающая вывод ракеты на орбиту, где управляемой величиной может быть, например, угол между осью ракеты и нормалью к Земле ==> см. рис. 1.1.4.а и рис. 1.1.4.б

1.2. Структура систем управления: простые и многомерные системы

В теории управления техническими системами часто бывает удобно систему разделить на набор звеньев, соединенных в сетевые структуры. В простейшем случае система содержит одно звено, на вход которого подается входной воздействие (вход), на входе получается отклик системы (выход).

В теории Управления Техническими Системам используют 2 основных способа представления звеньев систем управления:

— в переменных “вход-выход”;

— в переменных состояния (более подробно см. разделы 6…7).

Представление в переменных “вход-выход” обычно используется для описания относительно простых систем, имеющих один “вход” (одно управляющее воздействие) и один “выход” (одна регулируемая величина, см. рисунок 1.2.1).

Обычно такое описание используется для технически несложных САУ (систем автоматического управления).

В последнее время широкое распространение имеет представление в переменных состояния, особенно для технически сложных систем, в том числе и для многомерных САУ. На рис. 1.2.2 приведено схематичное представление многомерной системы автоматического управления, где u₁(t)…u_m(t) — управляющие воздействия (вектор управления), y₁(t)…y_p(t) — регулируемые параметры САУ (вектор выхода).

Рассмотрим более детально структуру САУ, представленную в переменных “вход-выход” и имеющую один вход (входное или задающее, или управляющее воздействие) и один выход (выходное воздействие или управляемая (или регулируемая) переменная).

Предположим, что структурная схема такой САУ состоит из некоторого числа элементов (звеньев). Группируя звенья по функциональному принципу (что звенья делают), структурную схему САУ можно привести к следующему типовому виду:

Рис. 1.2.3 — Структурная схема системы автоматического управления

Символом ε(t) или переменной ε(t) обозначается рассогласование (ошибка) на выходе сравнивающего устройства, которое может “работать” в режиме как простых сравнительных арифметических операций (чаще всего вычитание, реже сложение), так и более сложных сравнительных операций (процедур).

Задача системы управления состоит в том (если она устойчива), чтобы “работать” на уничтожение рассогласования (ошибки) ε(t), т.е. ==> ε(t) → 0.

Следует отметить, что на систему управления действуют как внешние воздействия (управляющее, возмущающее, помехи), так и внутренние помехи. Помеха отличается от воздействия стохастичностью (случайностью) своего существования, тогда как воздействие почти всегда детерминировано.

Для обозначения управляющего (задающего воздействие) будем использовать либо x(t), либо u(t).

1.3. Основные законы управления

Если вернуться к последнему рисунку (структурная схема САУ на рис. 1.2.3), то необходимо “расшифровать” роль, которую играет усилительно-преобразующее устройство (какие функции оно выполняет).

Если усилительно-преобразующее устройство (УПУ) выполняет только усиление (или ослабление) сигнала рассогласования ε(t), а именно: , где – коэффициент пропорциональности (в частном случае = Const), то такой режим управления замкнутой САУ называется режимом пропорционального управления (П-управление).

Если УПУ выполняет формирование выходного сигнала ε1(t), пропорционального ошибке ε(t) и интегралу от ε(t), т.е. , то такой режим управления называется пропорционально-интегрирующим (ПИ-управление). ==> , где b – коэффициент пропорциональности (в частном случае b = Const).

Обычно ПИ-управление используется для повышения точности управления (регулирования).

Если УПУ формирует выходной сигнал ε₁(t), пропорциональный ошибке ε(t) и ее производной, то такой режим называется пропорционально-дифференцирующим (ПД-управление): ==>

Обычно использование ПД-управления повышает быстродействие САУ

Если УПУ формирует выходной сигнал ε₁(t), пропорциональный ошибке ε(t), ее производной, и интегралу от ошибки ==> , то такой режим называетсято такой режим управления называется пропорционально-интегрально-дифференцирующим режимом управления (ПИД-управление).

ПИД-управление позволяет зачастую обеспечить “хорошую” точность управления при “хорошем” быстродействии

1.4. Классификация систем автоматического управления

1.4.1. Классификация по виду математического описания

По виду математического описания (уравнений динамики и статики) системы автоматического управления (САУ) подразделяются на линейные и нелинейные системы (САУ или САР).

Каждый “подкласс” (линейных и нелинейных) подразделяется на еще ряд “подклассов”. Например, линейные САУ (САР) имеют различия по виду математического описания.
Поскольку в этом семестре будут рассматриваться динамические свойства только линейных систем автоматического управления (регулирования), то ниже приведем классификацию по виду математического описания для линейных САУ (САР):

1) Линейные системы автоматического управления, описываемые в переменных «вход-выход» обыкновенными дифференциальными уравнениями (ОДУ) с постоянными коэффициентами:

где x(t) – входное воздействие; y(t) – выходное воздействие (регулируемая величина).

Если использовать операторную («компактную») форму записи линейного ОДУ, то уравнение (1.4.1) можно представить в следующем виде:

где, p = d/dt — оператор дифференцирования; L(p), N(p) — соответствующие линейные дифференциальные операторы, которые равны:

2) Линейные системы автоматического управления, описываемые линейными обыкновенными дифференциальными уравнениями (ОДУ) с переменными (во времени) коэффициентами:

В общем случае такие системы можно отнести и к классу нелинейных САУ (САР).

3) Линейные системы автоматического управления, описываемые линейными разностными уравнениями:

где f(…) – линейная функция аргументов; k = 1, 2, 3… — целые числа; Δt – интервал квантования (интервал дискретизации).

Уравнение (1.4.4) можно представить в «компактной» форме записи:

Обычно такое описание линейных САУ (САР) используется в цифровых системах управления (с использованием ЭВМ).

4) Линейные системы автоматического управления с запаздыванием:

где L(p), N(p) — линейные дифференциальные операторы; τ — время запаздывания или постоянная запаздывания.

Если операторы L(p) и N(p) вырождаются (L(p) = 1; N(p) = 1), то уравнение (1.4.6) соответствует математическому описанию динамики звена идеального запаздывания:

а графическая иллюстрация его свойств привдена на рис. 1.4.1

5) Линейные системы автоматического управления, описываемые линейными дифференциальными уравнения в частных производных. Нередко такие САУ называют распределенными системами управления. ==> «Абстрактный» пример такого описания:

Система уравнений (1.4.7) описывает динамику линейно распределенной САУ, т.е. регулируемая величина зависит не только от времени, но и от одной пространственной координаты.
Если система управления представляет собой «пространственный» объект, то ==>

где зависит от времени и пространственных координат, определяемых радиусом-вектором

6) САУ, описываемые системами ОДУ, или системами разностных уравнений, или системами уравнений в частных производных ==> и так далее…

Аналогичную классификацию можно предложить и для нелинейных САУ (САР)…

Для линейных систем выполеняются следующие требования:

Статической характеристикой называется зависимость выхода от величины входного воздействия в установившемся режиме (когда все переходные процессы затухли).

Для систем, описываемых линейными обыкновенными дифференциальными уравнениями с постоянными коэффициентами статическая характеристика получается из уравнения динамики (1.4.1) приравниванием нулю всех нестационарных членов ==>

На рис.1.4.2 представлены примеры линейной и нелинейных статических характеристик систем автоматического управления (регулирования).

Нелинейность членов, содержащих производные по времени в уравнениях динамики, может возникнуть при использовании нелинейных математических операций (*, /, , , sin, ln и т.д.). Например, рассматривая уравнение динамики некоторой «абстрактной» САУ

отметим, что в этом уравнении при линейной статической характеристики второе и третье слагаемые (динамические члены) в левой части уравнения — нелинейные, поэтому САУ, описываемая подобным уравнением, является нелинейной в динамическом плане.

1.4.2. Классификация по характеру передаваемых сигналов

По характеру передаваемых сигналов системы автоматического управления (или регулирования) подразделяются:

Системой непрерывного действия называется такая САУ, в каждом из звеньев которой непрерывному изменению входного сигнала во времени соответствует непрерывное изменение выходного сигнала, при этом закон изменения выходного сигнала может быть произвольным. Чтобы САУ была непрерывной, необходимо, чтобы статические характеристики всех звеньев были непрерывными.

Системой релейного действия называется САУ, в которой хотя бы в одном звене при непрерывном изменении входной величины выходная величина в некоторые моменты процесса управления меняется “скачком” в зависимости от величины входного сигнала. Статическая характеристика такого звена имеет точки разрыва или излома с разрывом.

Системой дискретного действия называется система, в которой хотя бы в одном звене при непрерывном изменении входной величины выходная величина имеет вид отдельных импульсов, появляющиеся через некоторый промежуток времени.

Звено, преобразующее непрерывный сигнал в дискретный сигнал, называется импульсным. Подобный вид передаваемых сигналов имеет место в САУ с ЭВМ или контроллером.

Наиболее часто реализуются следующие методы (алгоритмы) преобразования непрерывного входного сигнала в импульсный выходной сигнал:

На рис. 1.4.5 представлена графическая иллюстрация алгоритма амплитудно-импульсной модуляции (АИМ). В верхней части рис. представлена временная зависимость x(t) — сигнала на входе в импульсное звено. Выходной сигнал импульсного блока (звена) y(t) – последовательность прямоугольных импульсов, появляющихся с постоянным периодом квантования Δt (см. нижнюю часть рис.). Длительность импульсов – одинакова и равна Δ. Амплитуда импульса на выходе блока пропорциональна соответствующей величине непрерывного сигнала x(t) на входе данного блока.

Данный метод импульсной модуляции был весьма распространен в электронно-измерительной аппаратуре систем управления и защиты (СУЗ) ядерных энергетических установок (ЯЭУ) в 70-х…80-х годах прошлого столетия.

На рис. 1.4.6 представлена графическая иллюстрация алгоритма широтно-импульсной модуляции (ШИМ). В верхней части рис. 1.14 представлена временная зависимость x(t) – сигнала на входе в импульсное звено. Выходной сигнал импульсного блока (звена) y(t) – последовательность прямоугольных импульсов, появляющихся с постоянным периодом квантования Δt (см. нижнюю часть рис. 1.14). Амплитуда всех импульсов – одинакова. Длительность импульса Δt на выходе блока пропорциональна соответствующей величине непрерывного сигнала x(t) на входе импульсного блока.

Данный метод импульсной модуляции в настоящее время является наиболее распространенным в электронно-измерительной аппаратуре систем управления и защиты (СУЗ) ядерных энергетических установок (ЯЭУ) и САУ других технических систем.

Завершая данный подраздел, необходимо заметить, что если характерные постоянные времени в других звеньях САУ (САР) существенно больше Δt (на порядки), то импульсная система может считаться непрерывной системой автоматического управления (при использовании как АИМ, так и ШИМ).

1.4.3. Классификация по характеру управления

По характеру процессов управления системы автоматического управления подразделяются на следующие типы:

Выходной стохастический сигнал характеризуется:

Кроме приведенных основных видов классификации систем управления, существуют и другие классификации. Например, классификация может проводиться по методу управления и основываться на взаимодействии с внешней средой и возможности адаптации САУ к изменению параметров окружающей среды. Системы делятся на два больших класса:

1) Обыкновенные (несамонастраивающиеся) СУ без адаптации; эти системы относятся к разряду простых, не изменяющих свою структуру в процессе управления. Они наиболее разработаны и широко применяются. Обыкновенные СУ подразделяются на три подкласса: разомкнутые, замкнутые и комбинированные системы управления.

2) Самонастраивающиеся (адаптивные) СУ. В этих системах при изменении внешних условий или характеристик объекта регулирования происходит автоматическое (заранее не заданное) изменение параметров управляющего устройства за счет изменения коэффициентов СУ, структуры СУ или даже введения новых элементов.

Другой пример классификации: по иерархическому признаку (одноуровневые, двухуровневые, многоуровневые).

Источник