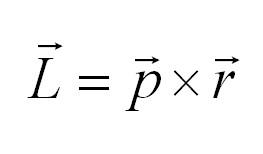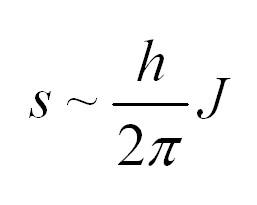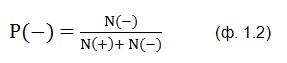в чем измеряется спин

В чем измеряется спин

Спин (от англ. spin — вертеть[-ся], вращение) — собственный момент импульса элементарных частиц, имеющий квантовую природу и не связанный с перемещением частицы как целого. Спином называют также собственный момент импульса атомного ядра или атома; в этом случае спин определяется как векторная сумма (вычисленная по правилам сложения моментов в квантовой механике) спинов элементарных частиц, образующих систему, и орбитальных моментов этих частиц, обусловленных их движением внутри системы.

В связи с этим говорят о целом или полуцелом спине частицы.

Существование спина в системе тождественных взаимодействующих частиц является причиной нового квантовомеханического явления, не имеющего аналогии в классической механике: обменного взаимодействия.

Содержание

Свойства спина

Любая частица может обладать двумя видами углового момента: орбитальным угловым моментом и спином.

В отличие от орбитального углового момента, который порождается движением частицы в пространстве, спин не связан с движением в пространстве. Спин — это внутренняя, исключительно квантовая характеристика, которую нельзя объяснить в рамках релятивистской механики. Если представлять частицу (например, электрон) как вращающийся шарик, а спин как момент, связанный с этим вращением, то оказывается, что поперечная скорость движения оболочки частицы должна быть выше скорости света, что недопустимо с позиции релятивизма.

Будучи одним из проявлений углового момента, спин в квантовой механике описывается векторным оператором спина алгебра компонент которого полностью совпадает с алгеброй операторов орбитального углового момента Однако, в отличие от орбитального углового момента, оператор спина не выражается через классические переменные, иными словами, это только квантовая величина. Следствием этого является тот факт, что спин (и его проекции на какую-либо ось) может принимать не только целые, но и полуцелые значения (в единицах постоянной Дирака ħ ).

Примеры

Ниже указаны спины некоторых микрочастиц.

На июль 2004 года, максимальным спином среди известных элементарных частиц обладает барионный резонанс Δ(2950) со спином 15/2. Спин ядер может превышать 20

История

В 1921 году опыт Штерна — Герлаха подтвердил наличие у атомов спина и факт пространственного квантования направления их магнитных моментов.

В 1924 году, ещё до точной формулировки квантовой механики, Вольфганг Паули вводит новую, двухкомпонентную внутреннюю степень свободы для описания валентного электрона в щелочных металлах. В 1927 году он же модифицирует недавно открытое уравнение Шрёдингера для учёта спиновой переменной. Модифицированное таким образом уравнение носит сейчас название уравнение Паули. При таком описании у электрона появляется новая спиновая часть волновой функции, которая описывается спинором — «вектором» в абстрактном (то есть не связанном прямо с обычным) двумерном спиновом пространстве.

В 1928 году Поль Дирак строит релятивистскую теорию спина и вводит уже четырёхкомпонентную величину — биспинор.

Математически теория спина оказалась очень прозрачной, и в дальнейшем по аналогии с ней была построена теория изоспина.

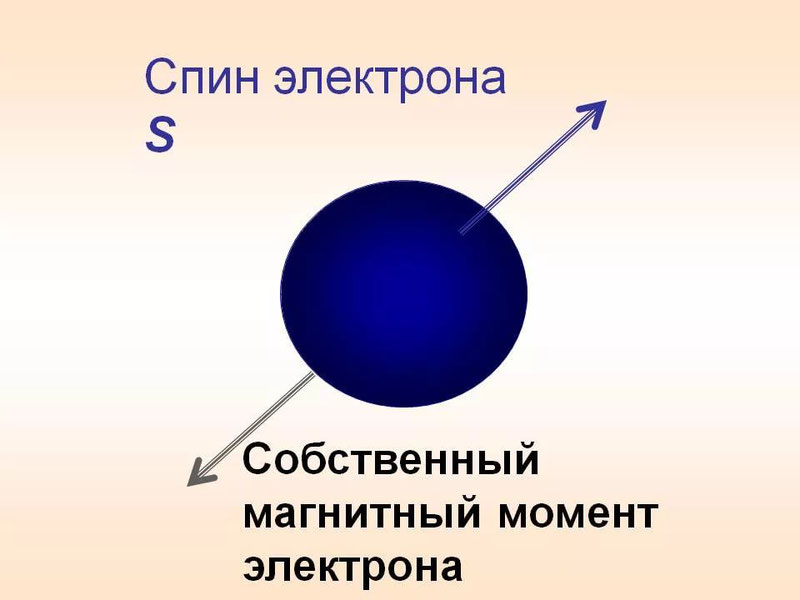
Спин и магнитный момент

Несмотря на то, что спин не связан с реальным вращением частицы, он тем не менее порождает определённый магнитный момент, а значит, приводит к дополнительному (по сравнению с классической электродинамикой) взаимодействию с магнитным полем. Отношение величины магнитного момента к величине спина называется гиромагнитным отношением, и, в отличие от орбитального углового момента, оно не равно магнетону ():

Спин и статистика

Вследствие того, что все элементарные частицы одного и того же сорта тождественны, волновая функция системы из нескольких одинаковых частиц должна быть либо симметричной (то есть не изменяется), либо антисимметричной (домножается на −1) относительно перестановки местами двух любых частиц. В первом случае говорят, что частицы подчиняются статистике Бозе — Эйнштейна и называются бозонами. Во втором случае частицы описываются статистикой Ферми — Дирака и называются фермионами.

Оказывается, именно значение спина частицы говорит о том, каковы будут эти симметрийные свойства. Сформулированная Вольфгангом Паули в 1940 году теорема о связи спина со статистикой утверждает, что частицы с целым спином ( s = 0, 1, 2, …) являются бозонами, а частицы с полуцелым спином ( s = 1/2, 3/2, …) — фермионами.

Обобщение спина

Введение спина явилось удачным применением новой физической идеи: постулирование того, что существует пространство состояний, никак не связанных с перемещением частицы в обычном пространстве. Обобщение этой идеи в ядерной физике привело к понятию изотопического спина, который действует в особом изоспиновом пространстве. В дальнейшем, при описании сильных взаимодействий были введены внутреннее цветовое пространство и квантовое число «цвет» — более сложный аналог спина.

Спин классических систем

В силу антисимметрии тензора Леви-Чивиты, 4-вектор спина всегда ортогонален к 4-скорости В системе отсчёта, в которой суммарный импульс системы равен нулю, пространственные компоненты спина совпадают с вектором момента импульса, а временная компонента равна нулю.

Именно поэтому спин называют собственным моментом импульса.

В квантовой теории поля это определение спина сохраняется. В качестве момента импульса и суммарного импульса выступают интегралы движения соответствующего поля. В результате процедуры вторичного квантования 4-вектор спина становится оператором с дискретными собственными значениями.

См. также

Примечания

Литература

Статьи

Полезное

Смотреть что такое «Спин» в других словарях:

СПИН — собственный момент импульса элементарной частицы или системы, образованной из этих частиц, напр. атомного ядра. Спин частицы не связан с её движением в пространстве и не может быть объяснён с позиций классической физики он обусловлен квантовой… … Большая политехническая энциклопедия

спин — а; м. [англ. spin вращение] Физ. Собственный момент количества движения элементарной частицы, атомного ядра, присущий им и определяющий их квантовые свойства. * * * спин (англ. spin, буквально вращение), собственный момент количества движения… … Энциклопедический словарь

Спин — Спин. Спиновый момент, присущий, например, протону, можно наглядно представить, связав его с вращательным движением частицы. СПИН (английское spin, буквально вращение), собственный момент количества движения микрочастицы, имеющий квантовую… … Иллюстрированный энциклопедический словарь

СПИН — (обозначение s), в КВАНТОВОЙ МЕХАНИКЕ собственный угловой момент, присущий некоторым ЭЛЕМЕНТАРНЫМ ЧАСТИЦАМ, атомам и ядрам. Спин может рассматриваться как вращение частицы вокруг своей оси. Спин является одним из квантовых чисел, посредством… … Научно-технический энциклопедический словарь

СПИН — (английское spin, буквально вращение), собственный момент количества движения микрочастицы, имеющий квантовую природу и не связанный с движением частицы как целого. Измеряется в единицах постоянной Планка h и может быть целым (0, 1, 2. ) или… … Современная энциклопедия

СПИН — (от англ. spin вращаться, вертеться), собственный момент кол ва движения элем. ч ц, имеющий квант. природу и не связанный с перемещением ч цы как целого. С. называют также собств. момент кол ва движения ат. ядра (и иногда атома); в этом случае С … Физическая энциклопедия

Спинёв — Спинёв, Николай Николаевич Спортивные награды Академическая гребля Олимпийские игры Золото Афины 2004 четвёрка Николай Николаевич Спинёв (род. 30 мая 1974, Ростов на Дону) российский спортсмен, олимпийский чемпион … Википедия

спин — (англ. spin вращаться) собственный механический момент количества движения элементарной частиц (электрона, протона, нейтрона) или атомного ядра, всегда присущий данному виду частиц, определяющий их свойства и обусловленный их квантовой природой;… … Словарь иностранных слов русского языка

спин — момент, вращение Словарь русских синонимов. спин сущ., кол во синонимов: 2 • вращение (15) • момент … Словарь синонимов

спин — спин, а (физ.) … Русский орфографический словарь

Источник

Что такое спин в физике: момент импульса, бозоны, фермионы

Итак, полностью абстрагируемся и забываем любые классические определения. Ибо спин – это понятие, присущее исключительно квантовому миру. Попробуем разобраться в том, что это такое.

Больше полезной информации для учащихся – у нас в телеграм.

Спин и момент импульса

Спин (от английского spin – вращаться) – собственный момент импульса элементарной частицы.

Теперь вспомним, что такое момент импульса в классической механике.

Момент импульса – это физическая величина, характеризующая вращательное движение, точнее, количество вращательного движения.

В классической механике момент импульса определяется как векторное произведение импульса частицы на ее радиус вектор:

По аналогии с классической механикой спин характеризует вращение частиц. Их представляют в виде волчков, вращающихся вокруг оси. Если частица имеет заряд, то, вращаясь, она создает магнитный момент и явлеятся своего рода магнитом.

Однако данное вращение нельзя трактовать классически. Все частицы помимо спина обладают внешним или орбитальным моментом импульса, характеризующим вращение частицы относительно какой-то точки. Например, когда частица движется по круговой траектории (электрон вокруг ядра).

Спин же является собственным моментом импульса, то есть характеризует внутреннее вращательное состояние частицы вне зависимости от внешнего орбитального момента импульса. При этом спин не зависит от внешних перемещений частицы.

Представить, что же там вращается внутри частицы, невозможно. Однако факт остается фактом – для заряженных частиц с разнонаправленными спинами траектории движения в магнитном поле будут различны.

Спиновое квантовое число

Для характеристики спина в квантовой физике введено спиновое квантовое число.

Спиновое квантовое число – одно из квантовых чисел, присущих частицам. Часто спиновое квантовое число называют просто спином. Однако следует понимать, что спин частицы (в понимании собственного момента импульса) и спиновое квантовое число – это не одно и то же. Спиновое число обозначается буквой J и принимает ряд дискретных значений, а само значение спина пропорционально приведенной постоянной Планка:

Бозоны и фермионы

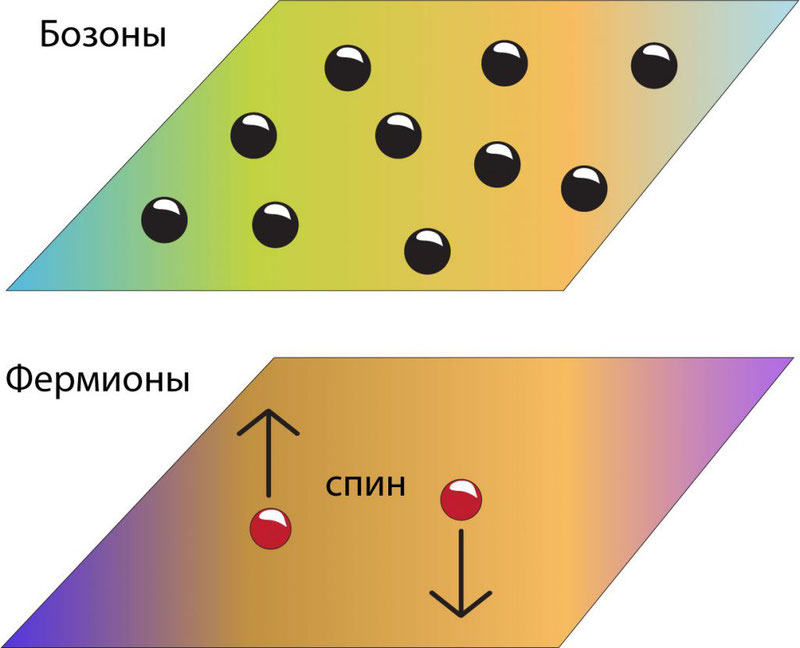
Разным частицам присущи разные спиновые числа. Так, главное отличие состоит в том, что одни обладают целым спином, а другие – полуцелым. Частицы обладающие целым спином называются бозонами, а полуцелым – фермионами.

Бозоны подчиняются статистике Бозе-Эйнштейна, а фермионы – Ферми-Дирака. В ансамбле частиц, состоящем из бозонов, любое их количество может находиться в одинаковом состоянии. С фермионами все наоборот – наличие двух тождественных фермионов в одной системе частиц невозможно.

Фермионы: электрон, лептон, кварк

Попробуем представить, чем отличаются частицы с разными спиновыми числами на примерах из макромира. Если спин объекта равен нулю, то его можно представить в виде точки. Со всех сторон, как ни вращай этот объект, он будет одинаков. При спине равном 1 поворот объекта на 360 градусов возвращает его в состояние, идентичное первоначальному состоянию.

Надеемся, что вы осилите эту теорию быстро и сможете при случае применить знания на практике. Ну а если задачка по квантовой механике оказалось непосильно сложной или не можете не забывайте о студенческом сервисе, специалисты которого готовы прийти на выручку. Учитывая, что сам Ричард Фейнман сказал, что «в полной мере квантовую физику не понимает никто», обратиться за помощью к опытным специалистам – вполне естественно!

Источник

В чем измеряется спин

Добавить в закладки

Вы сможете увидеть эту публикацию в личном кабинете

Добавить в закладки

Вы сможете увидеть эту публикацию в личном кабинете

Добавить в закладки

Вы сможете увидеть эту публикацию в личном кабинете

Добавить в закладки

Вы сможете увидеть эту публикацию в личном кабинете

Добавить в закладки

Вы сможете увидеть эту публикацию в личном кабинете

Добавить в закладки

Вы сможете увидеть эту публикацию в личном кабинете

Добавить в закладки

Вы сможете увидеть эту публикацию в личном кабинете

Добавить в закладки

Вы сможете увидеть эту публикацию в личном кабинете

Подпишитесь на нашу рассылку и получайте новости о последних проектах, мероприятиях и материалах ПостНауки

Источник

# чтиво | Что такое спин?

После того, как мы выяснили, что такое абсолютный ноль и можно ли восстановить информацию о том, что ела черная дыра, на повестке дня появился еще один интересный вопрос. Вопрос сложный, поскольку лежит в области квантовой физики. Звучит он примерно так:

Что еще за спин?

Если вы думаете, что экспрессия была лишней, вы ошибаетесь. Спин — одна из тех странных вещей в квантовой механике, пытаясь понять которые, вы думаете, что интуиция и личный жизненный опыт вам помогут. Но это не так. Напротив, ваша интуиция более вероятно упадет на колени перед вами. Попробуйте не доверять ей.

Начнем с того, что у всех частиц есть фундаментальный спин. Спин — «ось» от английского spin. Так же, как электрический заряд или масса, спин помогает определить тип частицы.

Некоторые частицы, вроде электронов, позитронов и кварков (протоны и нейтроны состоят из кварков, также фундаментальных частиц Стандартной модели), обладают спином ½. Они известны как «фермионы». Другие, фотоны, глюоны, а также W- и Z-частицы, обладают спином 1. Они известны как «бозоны». Очевидно, фермионы и бозоны ведут себя по-разному.

Если все это время вы согласно кивали, тонкий голосок у вас в голове, наверное, говорил что-то типа «полспина чего?». Стоит отметить, к внутреннему голосу по-хорошему нужно прислушиваться, поэтому давайте поговорим о том, как работает спин электрона.

Это как маленький гироскоп, но не совсем.

Почему электроны? Потому что если вы поймете, что такое спин электрона, все остальное будет простым. Попробуйте представить, что электрон — это маленький гироскоп. Он вращается и вертится без остановки. Вне зависимости от того, что вы делаете с ним, вы не можете замедлить или ускорить вращение электрона; вы просто можете изменить его положение.

Что бы вы ни делали, у электрона всегда будет спин ½. Но ½ чего? Числа, известного как «приведенная постоянная Планка». Это очень маленькое число. Очень.

Вот вам первый странный факт. Обычно вы можете замедлить вращающееся тело. Супермен смог остановить вращение Земли, например.

С другой стороны, мы имеем дело с маленьким вращающимся гироскопом. Угловой момент — это одна из тех постоянных величин, которые сводят с ума физиков. При изменении направления спина электрона, угловой момент передается куда угодно — от орбиты до другого электрона.

Поскольку у электрона есть заряд, и поскольку он «вращается по оси», он создает небольшое магнитное поле. Так работает любой электромагнит. Мы можем обнаружить магнитное поле электрона или отклонить отдельные электроны, используя другие магниты, чтобы выяснить, в каком направлении вращается электрон. Но…

Магнитное поле работает совсем не так.

Возьмите маленький заряженный шарик и закрутите его вокруг оси. Вы создадите магнит. Вне зависимости от того, насколько велик или мал шар, оказывается, что магнитное поле будет точно предсказано кратным угловым моментом. Есть куча констант, связанных с зарядом и массой шарика, но не с размером.

Проблема в том, что если представить электрон таким же образом, описанная выше процедура не прокатит вообще. Магнитное поле будет в два раза больше. Точнее, в 2,0023193044 раза. Это число измерено с безумным уровнем точности и вычислено теоретически. В игру вступает эта чертова «квантовая теория поля», потому что мы можем сделать несколько точных предсказаний.

Странный факт номер два: вы не можете, не имеете права думать об электроне, как о маленькой микроскопической заряженной сфере. Просто получатся неправильные цифры.

Хотя у электронов есть фиксированный спин, вы можете предположить, что компоненты спина в определенном направлении могут принимать любое старое значение, которое нам нравится. Подумайте об этом в следующем примере. Допустим, у меня была метровая палка (длиной в 1 метр), одним концом воткнутая в землю под углом. Вы можете измерить высоту от верхнего конца до земли, и в зависимости от угла, получите значение между 0 и 1 метром.

Вы знаете, что Земля вращается, но если вы когда-нибудь видели глобус, вы в курсе, что он наклонен где-то под углом 23 с половиной градуса по отношению к плоскости орбиты. Другими словами, если вы измерите «ось» (или спин) Земли сверху донизу, вы получите меньше, чем полную длину оси. Ось представляется немного расшатанной из стороны в сторону.

С электронами такое не работает. Если вы создали небольшое магнитное поле, чтобы различить их, вы выясните, что отдельный электрон в 100 % случаев вертится вверх и в 100 % случаев вертится вниз, в зависимости от случая, и никогда — между. Что более странно, не имеет значения, как вы будете настраивать свою измерительную аппаратуру, вы всегда придете к одному и тому же начальному результату: либо одна сторона, либо другая, третьего не дано.

И здесь у нас рождается третий странный факт. Предположим, вы измеряете электрон и выясняете, что он обладает верхним спином. После вы пытаетесь измерить спин слева-направо. Здравый смысл подскажет вам, что число будет равно нулю, так как вы знаете, что электрон вертится снизу вверх, а не слева направо. Но как мы отмечали выше, здравый смысл вам не поможет. Выясняется, что: а) в половине случаев, когда вы измеряете электрон, он будет «слева», в половине — «справа», и б) право и лево определяется абсолютной случайностью. Правда. Ничто во вселенной не сможет сказать вам, какую сторону выберет электрон. Такого рода случайность сильно огорчала Эйнштейна (вспомните его высказывание о том, что Бог не играет в кости).

Вам нужно дважды повернуть электрон, чтобы он выглядел, «как прежде»

Это четвертый странный факт. Вам нужно дважды повернуть электрон вокруг оси, и он будет выглядеть так же, как и в начале.

Тот же эффект возникнет, если вы представите, будто подменяете один электрон другим. Ничего не меняется, только появляется знак минус перед всей волновой функцией. Кажется незначительным, пока вы не поймете, что…

Знак минус — это то, что делает вас возможным.

Другой способ сказать это: электроны (и все фермионы: кварки, позитроны, нейтрино и т.д.) не могут находиться в одном и том же месте с одним и тем же спином. Это знаменитый «запрет Паули». Он предсказывает, что электроны в атомах не могут быть в одном и том же состоянии, но вместе этого занимают разные орбитали. Если бы все было не так, электроны занимали бы самые низкие уровни, и элементы вели бы себя скучновато, как водород. Скучно и не способствует зарождению жизни.

Бозоны, другой тип частиц, не работают по этому принципу. Поменяйте местами два бозона, и ничего не изменится. Поверните бозон единожды, и все вернется в нормальное русло. У них спин равен одному, что означает только то, что они ведут себя точно так, как вы ожидаете. Но таковы лишь бозоны, обнаруженные на сегодняшний день. У бозона Хиггса (если он существует) спин 0, у гравитона (если он существует) спин 2, но мы пока можем о них не говорить. Бозоны могут находиться в одном месте и обладать одним и тем же спином. Вот почему мы можем получить конденсат Бозе-Эйнштейна, который представляет собой кучу бозонов в одном состоянии.

«Фишка» не в том, что спин — странная штука, хотя с этим никто не спорит. «Фишка» в том, что спин лежит в центре куда более серьезных и фундаментальных вещей, в основе их работы, чем вы можете подозревать.

Источник

В чем измеряется спин

Физические эксперименты всегда подразумевают измерение каких-либо величин. В экспериментах по схеме Белла, мы будем измерять спин элементарных частиц, поэтому нам следует разобраться, что же это за штука такая.

Спин элементарной частицы – это её момент импульса. Можно считать, что частица – это шарик, который вращается вокруг собственной оси, как, например, наша планета. Такое представление, вообще-то, довольно примитивно, но для нашей задачи сгодится. Надо только понимать, что спин, в отличие от классического момента импульса – величина квантовая, и поэтому обладает некоторыми специфическими особенностями, которые мы ниже рассмотрим.

Момент импульса тела может быть любым как по направлению, так и по абсолютной величине. Спин частицы по абсолютной величине может принимать только одно из небольшого набора значений (количество возможных значений определяется типом частицы). Иными словами, спин квантуется. А вот направление спина частицы может быть любым. Стало быть, измерять мы будем именно направление спина.

Ну что же, перейдём к «практической» части. Нет, это ещё не белловские эксперименты, для начала мы проделаем несколько простых опытов, чтобы лучше понять свойства спина и поупражняться с его измерением.

Для измерения спина частиц используют устройство, которое называется «прибор Штерна-Герлаха», по фамилиям его изобретателей. Дальше мы будем называть это устройство сокращено: «ПШГ». Кратко рассмотрим принцип действия прибора.

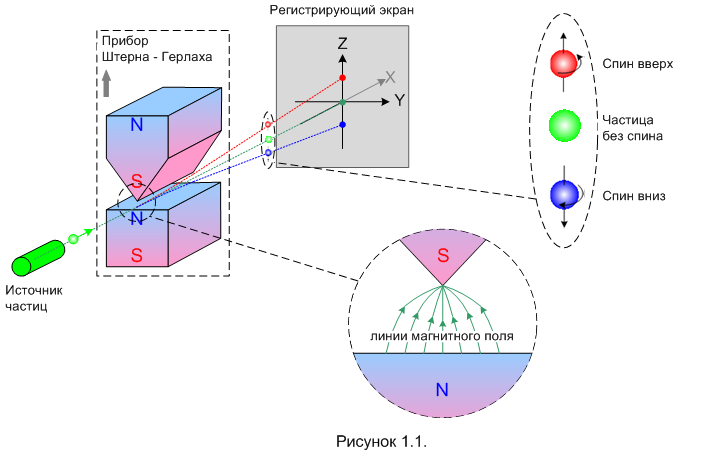
Элементарная частица имеет электрический заряд* и вращается, а значит, она представляет собой маленький магнит. Другими словами, если у частицы есть спин, значит, у неё есть и магнитные свойства, или, говоря более научно – магнитный момент. Вот этот-то магнитный момент вращающейся частицы и использует ПШГ. Устройство ПШГ, а также прочее оборудование, необходимое для опытов, показаны на рисунке 1.1.

Собственно, сам ПШГ состоит из двух магнитов. Верхний и нижний магниты имеют различную форму, благодаря чему магнитное поле в промежутке между ними неоднородно. Также на рисунке изображены источник частиц, (надо же их откуда-то брать?) и экран, который регистрирует точку попадания частицы. Например, в качестве экрана может использоваться фотопластинка: попавшая в неё частица «засвечивает» точку попадания.

Итак, источник выпускает частицу в направлении оси X. Затем частица попадает в ПШГ и проходит через зазор между магнитами. Если частица не обладает спином, то магнитное поле на неё никак не влияет, она движется по прямой и попадает в центр экрана – его мы приняли за начало координат. Траектория такой частицы показана на рисунке зелёной линией. На самом деле мы тут будем «работать» только с частицами, обладающими ненулевым спином, так что зелёную траекторию я нарисовал чисто для того, чтобы обозначить центр экрана.

Если спин направлен вверх, то неравномерное магнитное поле в зазоре отклоняет частицу вверх (красная траектория). Если спин направлен вниз, то частица отклоняется вниз (синяя траектория). Таким образом, наблюдая на экране точку попадания частицы, мы определяем, как был направлен её спин – вверх или вниз.

Мы рассмотрели случаи, когда спин частицы направлен вдоль оси Z. То есть, направление спина совпадает с ориентацией прибора или строго противоположно ей. Но ведь спин частицы может быть ориентирован в пространстве как угодно. Возникает вопрос: а что же будет с частицей, если её спин и ориентация ПШГ не совпадают? Тут классическая физика и квантовая механика дают разные ответы.

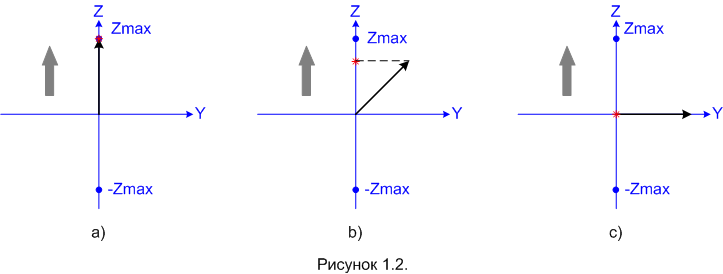
Если рассматривать ситуацию чисто «классически», и представлять себе частицу как вращающийся заряженный шарик, то ответ будет такой: отклонение частицы пропорционально проекции её спина на направление ориентации прибора (в нашем случае это то же самое, что ось Z). То есть, максимальное отклонение точки попадания от центра экрана будет у тех частиц, у которых спин направлен параллельно оси Z (Рисунок 1.2-a, точка «Zmax»). Разумеется, если спин параллелен оси Z, но направлен в противоположную сторону, то частица попадёт в точку «–Zmax».

Отклонения частицы по оси Y при такой ориентации прибора (напоминаю – она показана толстой серой стрелкой) быть не должно.

Ось X на рисунке 1.2 и на следующих рисунках не показана, чтобы не загромождать. Можете считать, что она направлена от нас прямо вглубь рисунка. Места попадания частиц в регистрирующий экран показаны красной звёздочкой. Направление спина показано так, как мы условились раньше: тонкой чёрной стрелкой.

Квантовая механика предсказывает совершенно другой результат: все частицы будут отклоняться на максимально возможное расстояние и попадать только в одну из двух точек, причём, линия, походящая через эти две точки и центр экрана, будет параллельна ориентации прибора. В нашем случае, когда ПШГ ориентирован параллельно оси Z, это будут точки либо «Zmax», либо «–Zmax». В этом, собственно, и заключается «квантовость». Если в «классике» мы можем намерять любое отклонение, а значит и направление момента импульса, то в квантовой механике направление спина «квантуется»: есть только два возможных результата измерения.

Тут, чтобы вас не запутать на будущее, я должен оговорить вот что: на самом деле два результата измерения мы получим только на частицах со спином 1/2. К таким частицам относятся, в частности, электроны, протоны, нейтроны и некоторые другие. Для прочих частиц возможны три результата, четыре, пять и так далее, но в любом случае число возможных результатов будет конечным. Чтобы не делать в дальнейшем таких оговорок, давайте определимся: мы будем в наших экспериментах работать только с протонами.

Итак, классическая физика и квантовая механика предсказывают разные результаты опытов с протонами. Ну что же, вооружившись банальностью «опыт – критерий истины» приступим к экспериментальной проверке.

Установка для опыта у нас уже есть, она показана на рисунке 1.1. Только там у нас был «источник частиц», теперь это будет источник конкретно протонов.

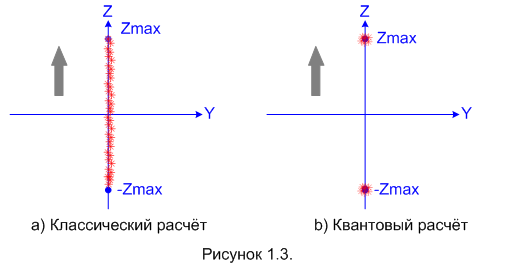
Предполагаем, что источник выпускает протоны со случайно ориентированным спином. Значит, если права классическая физика, то протоны должны попадать в экран со случайным отклонением по оси Z в диапазоне от «–Zmax» до «Zmax». Тогда, если мы выпустим достаточно много протонов, то картинка на экране должна будет выглядеть так, как показано на рисунке 1.3-a. То есть, будет сплошная полоса попаданий.

Ну а если права квантовая механика, то после серии «выстрелов» на экране будет картинка как на рисунке 1.3-b: только два варианта попаданий. Причём, попадания распределятся примерно пополам: половина вверх, половина вниз.

В реальности такой эксперимент даёт картинку в полном соответствии с предсказаниями квантовой механики, как на рисунке 1.3-b. Это один из тех экспериментов, о которых я говорил во введении: с точки зрения классической физики его результаты объяснить не удаётся, а квантовая механика объясняет их «на раз».

Сторонники классического подхода тут могут «уцепиться за соломинку»: мол, мы предположили, что спин протонов, испускаемых источником, ориентирован случайно, а вдруг это не так? Возможно, источник выпускает протоны, ориентированные только вертикально, вдоль оси Z. В таком случае «классический» расчёт даст такую же картину распределения попаданий, как и квантовый (рисунок 1.3-b).

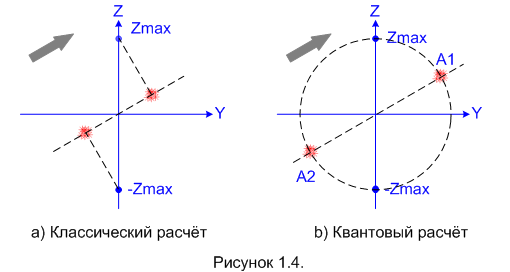
Хорошо, мы это можем легко проверить. Повернём ПШГ на некоторый угол вокруг оси X и проделаем опять длинную серию «выстрелов». Если версия «классиков» верна, то мы увидим на экране картинку типа 1.4-a. Ну а если всё же правда на «квантовой» стороне, то картинка будет как 1.4-b.

Разобрались? Отлично, тогда едем дальше. Проделав эксперимент с «повёрнутым» ПШГ (на рисунке 1.4 он повёрнут вокруг оси X на 60 градусов вправо), убеждаемся, что результаты опыта совпадают с квантовыми предсказаниями: половина (приблизительно) протонов попадает в точку A1, половина – в точку A2. Для верности можем провести эксперименты с разными углами поворота ПШГ и убедиться: результат всегда таков, как предсказывает квантовая механика. Заодно мы убедимся в том, что наше предположение о случайной ориентации спинов на входе прибора было правильным.

Итак, констатируем важный вывод, на который мы будем ссылаться в дальнейших рассуждениях:

Утверждение 1.1.

Вне зависимости от того, с каким направлением спина протон входит в измерительный прибор, мы получим только один из двух возможных результатов измерения: направление спина протона либо совпадает с ориентацией прибора, либо строго противоположно ему.

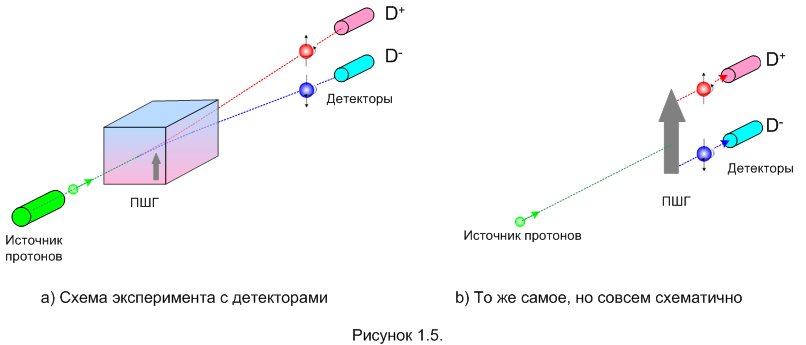
Для порядка отмечу, что в нашем случае измерительным прибором является устройство, включающее ПШГ и регистрирующий экран. Однако, утверждение 1.1. верно и для любого другого устройства, измеряющего направление спина. Но мы будем и дальше пользоваться прибором Штерна-Герлаха. Только вот, в свете утверждения 1.1., регистрирующий экран нам больше не нужен. Поскольку из ПШГ все протоны выходят только по одной из двух возможных траекторий, мы можем вместо экрана поставить на каждой траектории детектор протонов. Теперь схема эксперимента, показанного на рисунке 1.1, будет выглядеть так, как на рисунке 1.5-a.

Детекторы обозначены как D + (плюс – детектор) и D – (минус – детектор). В плюс – детектор будут попадать все протоны, направление спина которых совпадает с ориентацией прибора. В минус – детектор попадут все протоны с противоположной прибору ориентацией.

Разумеется, если мы теперь захотим покрутить ПШГ вокруг «линии выстрела», показанной на рисунке зелёным пунктиром, то мы должны будем соответствующим образом переместить и детекторы, иначе все «выстрелы» уйдут в «молоко». Чтобы не мучится с определением нового положения детекторов, мы можем просто объединить ПШГ и детекторы в единую конструкцию и вращать её всю целиком так, как нам требуется. Дальше при описании опытов я буду эту измерительную конструкцию изображать так, как показано на рисунке 1.5-b.

Итак, мы выяснили, что ПШГ направляет входные протоны по одной и из двух возможных траекторий. Дальше эти траектории будем называть так: «плюс-канал» и «минус-канал». Выше, на рисунках 1.1, 1.5, протон в плюс-канале (красный) я изобразил со спином вверх, а протон в минус-канале (синий) со спином вниз. Но это было сделано, так сказать, «авансом», на самом деле мы пока не уверены, что протоны выходят из прибора именно в таких состояниях. Есть ведь серьёзные поводы для сомнений.

Во-первых, может быть, вообще никакого спина у протона не существует, а ПШГ просто разбрасывает протоны по каналам каким-то случайным или псевдослучайным образом, как, например, фонтан разбрасывает водяные брызни?

Во-вторых, в «классическом» случае, если бы мы действительно имели дело с вращающимися заряженными шариками без всяких квантовых свойств, шарик отклонялся бы в неравномерном магнитном поле, но его момент импульса при этом бы не изменился: какой на входе, такой и на выходе. Другими словами, «классическое» измерение не меняет измеряемой величины. Может быть и в квантовом случае такая картина: с каким протон спином вошел в прибор, с таким и вышел?

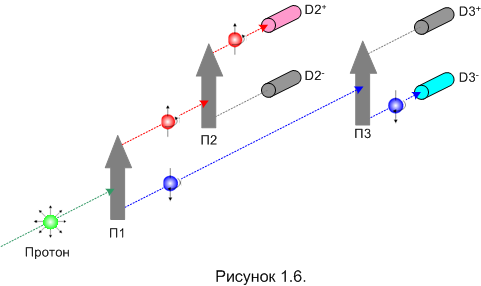
Для начала проведём эксперимент, который должен развеять наши сомнения на счёт «во-первых» (рисунок 1.6).

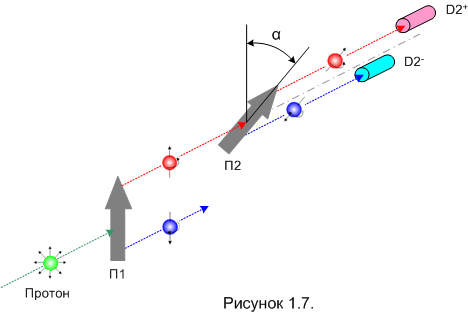
Чтобы дальше исследовать свойства спина, проделаем следующий эксперимент. (рисунок 1.7).

Вероятность срабатывания плюс-детектора D2 + :

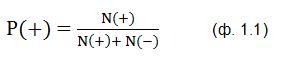
где:

Соответственно, вероятность срабатывания минус-детектора D2 – :

Как не трудно догадаться, вероятности P(+) и P(–) в сумме всегда дают единицу

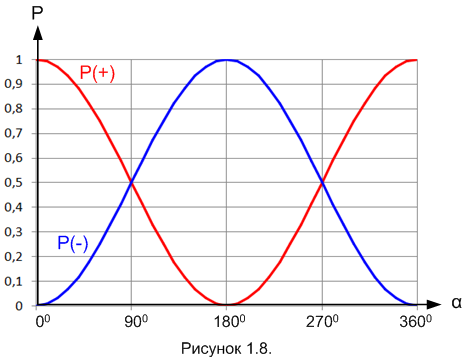
Итак, мы получили вероятности срабатывания того или иного детектора при α = 1°. Аналогичным образом мы можем проделать опыт для любых значений угла, и получить графики зависимости вероятностей P(+) и P(–) от угла α. Эти графики будут выглядеть так (рисунок 1.8).

А вот формулы этих зависимостей:

Утверждение 1.2:

Отметим «особые» случаи:

Если угол между ориентациями приборов П1 и П2 равен 0° (направления совпадают), то протон гарантировано попадает в плюс-детектор (вероятность этого события равна единице) и никогда не попадёт в минус-детектор.

Если угол равен 180° (направления противоположны), то ситуация обратная: будет срабатывать только минус-детектор.

Если угол равен 90° или 270° градусов (ориентации приборов перпендикулярны), то вероятности срабатывания плюс-детектора и минус-детектора одинаковы и равны 0,5.

При всех прочих значениях углов вероятности срабатывания плюс-детектора и минус-детектора будут различными, но в сумме они всё равно дадут единицу.

Для объяснения этих результатов можно предложить две версии.

Версия 1. Спин протона влияет на его «сортировку» при прохождении ПШГ. Но сам спин при этом не меняется.

Версия 2. Спин протона не только влияет на его «сортировку» при прохождении ПШГ, но и меняется при этом: в плюс-канале направление спина совпадает с ориентацией ПШГ, а в минус-канале направления противоположны.

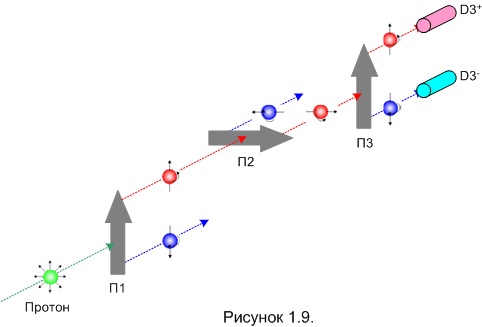
Очередной эксперимент (рисунок 1.9) поможет нам выяснить, какая из этих версий правильная.

Если верна версия 1 (спин протона при прохождении ПШГ не меняется), то будет срабатывать только плюс-детектор. Надо объяснять почему?

Так вот, если мы реально проведём такой эксперимент, то увидим, что с равной вероятностью срабатывают оба детектора. Значит, верна версия 2.

Вернёмся чуть назад, к предыдущему опыту (рисунок 1.7) и его результатам (рисунок 1.8). Теперь мы точно знаем, что в плюс-канале П1 оказываются только те протоны, направление спина которых совпадает с ориентацией П1. А значит, утверждение 1.2 (формулы (ф. 1.3), (ф. 1.4)) определяют вероятности попадания протона в плюс-канал или в минус-канал в зависимости от угла между направлением спина протона и ориентацией прибора.

Кстати, обращаю внимание: утверждение 1.2. исчерпывающе объясняет результаты всех проделанных нами опытов, а также «поглощает» утверждение 1.1, сделанное в предыдущей части.

Теперь мы можем сформулировать обозначенную во введении проблему (детерминизм или случайность) на нашем конкретном примере. Посмотрите ещё раз на ситуацию, когда направление спина протона и ориентация прибора не параллельны. В этом случае может сработать либо плюс-детектор, либо минус-детектор. Классический (детерминистский) и квантовый (случайный) подход объясняют эту неопределённость по разному.

В самых популярных статейках такой квантовый подход принято «объяснять» ещё следующим образом: протон перед попаданием в измеритель находится в двух состояниях одновременно (погуглите на тему «кот Шредингера»). А в измерителе протон скачкообразно переходит в одно из этих состояний. В более серьёзных статьях говорят, что перед попаданием в измеритель протон находится в суперпозиции состояний. А при измерении происходит разрушение суперпозиции (оно же – коллапс волновой функции, оно же – редукция).

Какой из двух подходов правильный – классический или квантовый? Как раз это мы и будем выяснять в «следующих сериях».

*Некоторые электрически нейтральные частицы, нейтрон, например, тоже обладают магнитным моментом. Но физический механизм этого явления мы тут рассматривать не будем, это к нашей теме не относится.

Источник