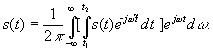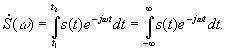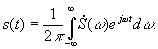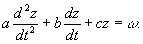в чем измеряется спектральная плотность

Энергетические характеристики сигналов. Спектральная плотность энергии

DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов

Распространяется под лицензией LGPL v3

Заметим, что скалярное произведение сигнала с самим собой возвращает энергию данного сигнала:

связывающее среднюю мощность периодического сигнала. Для непериодических сигналов мы можем получить аналогичное равенство энергии сигнала во времени и в частотной области. Для этого в обобщенную формулу Рэлея подставим и получим:

было введено понятие спектральной плотности сигнала и была приведена аналогия поясняющая понятие спектральной плотности, и ее отличие от спектра периодического сигнала.

Из равенства (9) следует, что энергия сигнала может быть представлена как интеграл по всей оси частот:

Сделаем важное замечание. Спектральная плотность энергии игнорирует ФЧХ сигнала. Тогда можно заключить, что одной и той же спектральной плотности энергии могут соответствовать множество различных сигналов, имеющих одинаковую АЧХ и различные ФЧХ.

и на практике анализ поведения убывающей спектральной плотности с ростом частоты имеет важное значение. Однако графический анализ бывает затруднителен ввиду высокой скорости убывания спектральной плотности по частоте, а в случае спектральной плотности энергии затруднителен вдвойне, поскольку возведение АЧХ в квадрат только ускоряет убывание. Поэтому широкое распространение получило представление спектральной плотности энергии в логарифмическом масштабе, выраженной в единицах децибел (дБ):

В качестве примера на рисунке 1 приведены спектральные плотности энергии прямоугольного, треугольного, двустороннего экспоненциального и гауссова импульсов в линейном и логарифмическом масштабе.

Как видно из рисунка 1а, спектральные плотности энергии импульсов в линейном масштабе практически сливаются и очень сложно различимы.

Логарифмическая шкала представления спектральной плотности энергии оказывается удобной при сравнении характеристик сигналов. Если энергии двух сигналов отличаются в 100 раз, то в логарифмической шкале отношение их энергий составляет 20 дБ. Если же энергии отличаются в 1000000 раз, то в логарифмической шкале это соответствует 60 дБ. Удвоение энергии сигнала, в логарифмической шкале соответствует прибавлению 3 дБ.

В данном разделе мы рассмотрели энергетические характеристики периодических и непериодических сигналов. Мы показали, что периодические сигналы имеют бесконечную энергию, но конечную среднюю мощность. Средняя мощность непериодических сигналов стремится к нулю, а их энергия конечна.

Было введено понятие скалярного произведения сигналов и получена обобщенная формула Релея,связывающая скалярное произведение во временной и частотной областях.

Установлено равенство Парсеваля для непериодических сигналов, как частный случай формулы Релея.

Введено понятие спектральной плотности энергии как квадрата модуля спектральной плотности сигнала. Также рассмотрено представление спектральной плотности энергии в линейном и логарифмическом масштабе для различных сигналов.

Источник

Спектральная плотность

В теории управления существуют и взаимно дополняют друг друга два подхода:

1) временнóй – исследование процессов во времени;

2) частотный – исследование частотных свойств сигналов и систем (с помощью передаточных функций и частотных характеристик).

Аналогичная ситуация наблюдается и при рассмотрении случайных процессов. Основная временная характеристика стационарного процесса – это корреляционная функция, а частотные свойства описываются спектральной плотностью.

Спектральная плотность – это функция, которая показывает распределение мощности сигнала по частотам. Такая информация о полезных сигналах, помехах и возмущениях очень важна для разработчика систем управления. Система должна быть спроектирована так, чтобы усиливать сигналы с «полезными» частотами и подавлять «вредные» частоты, характерные для помех и возмущений.

Для перехода от временнóго описания детерминированных (не случайных) процессов к частотному, используют преобразования Фурье и Лапласа. Аналогично спектральная плотность случайного процесса может быть найдена как преобразование Фурье от корреляционной функции[4]:

.

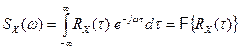
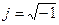
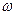
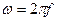
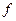
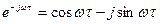
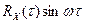
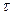
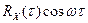
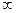
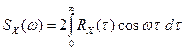
Здесь – мнимая единица, а – угловая частота в рад/с ( , где – «обычная» частота в герцах). Используя формулу Эйлера, можно представить экспоненту в виде сумму вещественной (косинусной) и мнимой (синусной) составляющих: . Функция – нечетная по , поэтому интеграл от нее в симметричных пределах равен нулю. Напротив, функция – четная, так что при интегрировании можно взять интервал от 0 до и удвоить результат:

.

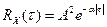
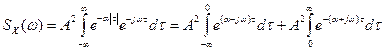
Спектральная плотность случайного процесса, имеющего корреляционную функцию , вычисляется как

.

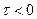
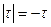
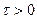
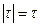
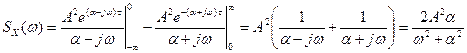
Интервал интегрирования разбит на две части. При имеем , а при – . Выполняя интегрирование, получаем

.

На рисунке слева показана корреляционная функция, а справа – соответствующая ей спектральная плотность мощности:

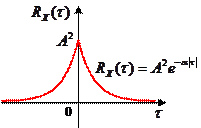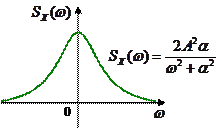Свойства спектральной плотности:

1) это неотрицательная, четная функция угловой частоты 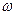(график расположен выше оси абсцисс и симметричен относительно вертикальной оси);

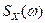
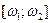
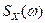
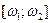
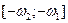
2) интеграл от на некотором интервале частот дает мощность, которая связана с этими частотами; поскольку функция – четная, результат интегрирования на нужно удвоить, чтобы учесть также и полосу ;

3) площадь под кривой определяет средний квадрат случайного процесса (для центрированного процесса он равен дисперсии):

.

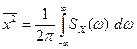
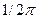
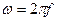
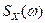
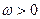
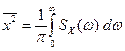
Множитель нужен для согласования единиц измерения, поскольку угловая частота измеряется не в герцах, а в рад/с. Учитывая, что функция четная, можно интегрировать ее только при , а результат удвоить:

.

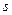
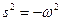
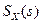
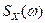
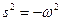
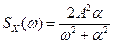
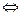
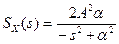
В теории управления нередко записывают спектральную плотность как функцию комплексной переменной , связанной с угловой частотой по формуле (отсюда следует ). Хотя это не совсем корректно с точки зрения математики, мы будем использовать запись для обозначения спектральной плотности , в которой выполнена замена :

.

Дата добавления: 2014-12-09 ; просмотров: 8229 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Спектральная плотность

В дальнейшем мы будем рассматривать в довольно общем виде, что сигнал представлен x ( t ), действительной функцией действительной переменной (времени), соответствующей физической величине размерности [единица].

Резюме

Спектральная плотность энергии

Это априори сложная функция действительной переменной, и мы имеем наоборот:

Спектральная плотность энергии сигнала x определяется следующим образом:

D S E знак равно Δ | Икс ( ж ) | 2 знак равно Икс ( ж ) Икс * ( ж ) <\ Displaystyle <\ rm > \; <\ stackrel <\ Delta><=>> \; | X (f) | ^ <2>= X (f) X ^ <*>(f)>

Тогда теорема Парсеваля-Планшереля гарантирует, что

Если x соответствует случайному процессу, спектральная плотность энергии фактически определяется математическим ожиданием (если оно существует):

D S E знак равно Δ E [ | Икс ( ж ) | 2 ] <\ Displaystyle <\ rm > \; <\ stackrel <\ Delta><=>> \; E \ left [| X (f) | ^ <2>\ right]>

Спектральная плотность мощности

Если x ( t ) не является суммируемым квадратом (что имеет место для большинства стационарных случайных процессов), X ( f ) не определяется в смысле функций (тем не менее, его можно определить в смысле распределений ): полная энергия в общем случае бесконечен (опять же, это верно для большинства стационарных случайных процессов).

Затем мы определяем усеченную версию x _T ( t ) функции x ( t ) следующим образом:

Если x представляет собой случайный процесс, мы определяем DSP спектральной плотности мощности (если он существует) следующим образом:

(который почти по определению не зависит от t для стационарного процесса).

Теорема Винера-Хинчина настолько тесно связана с определением и использованием спектральной плотности мощности, что некоторые авторы напрямую определяют DSP с помощью преобразования Фурье автокорреляции сигнала. Затем этот подход упрощает теорему Винера-Хинчина.

Без дополнительных пояснений, когда мы говорим о «спектральной плотности», обычно мы хотим говорить о S _x OS ( f ). Тем не менее некоторые авторы могут говорить о «двусторонней спектральной плотности мощности», не объясняя ее, и следует проявлять максимальную осторожность. [исх. required] В любом случае измеритель, возвращающий оценку PSD с использованием выборки данных, указывает одностороннюю PSD. Это, в частности, относится к анализатору быстрого преобразования Фурье (БПФ), обычно используемому в электронике для оценки DSP.

Оценка спектральной плотности мощности

Вот неполный список методов, используемых для оценки PSD на основе ограниченной выборки данных:

Источник

Спектральная плотность мощности

Спектральная плотность мощности (СПМ) в физике и обработке сигналов — функция, задающая распределение мощности сигнала по частотам. Её значение имеет размерность мощности, делённой на частоту, то есть энергии.

Содержание

Формальное определение

Пусть — сигнал, рассматриваемый на промежутке времени . Тогда энергия сигнала на данном интервале равна:

= = = ,

где — спектральная функция сигнала. При , средняя мощность (дисперсия)

.

— спектральная плотность мощности (функция плотности спектра мощности).

Спектр плотности мощности сигнала сохраняет информацию только об амплитудах спектральных составляющих. Информация о фазе теряется. Поэтому все сигналы с одинаковым спектром амплитуд и различными спектрами фаз имеют одинаковые спектры плотности мощности.

Методы оценки

Оценка СПМ может выполняться методом преобразования Фурье, предполагающего получение спектра в области частот посредством быстрого преобразования Фурье (БПФ). До изобретения алгоритмов БПФ этот метод из-за громоздкости прямого вычисления дискретного преобразования Фурье (ДПФ) практически не использовался. Предпочтение отдавалось другим методам, в частности, методу корреляционной функции (Блэкмена-Тьюки) и периодограммному методу.

См. также

Литература

Полезное

Смотреть что такое «Спектральная плотность мощности» в других словарях:

Спектральная плотность мощности шума прибора СВЧ — 221. Спектральная плотность мощности шума прибора СВЧ Спектральная плотность мощности шума Noise spectral power density Pш Мощность шума прибора СВЧ в полосе 1 Гц Источник: ГОСТ 23769 79: Приборы электронные и устройства защитные СВЧ. Термины,… … Словарь-справочник терминов нормативно-технической документации

Спектральная плотность мощности шумового диода — 140. Спектральная плотность мощности шумового диода G Отношение среднего квадратического значения мощности шумового диода к заданному диапазону частот Источник: ГОСТ 25529 82: Диоды полупроводниковые. Термины, определения и буквенные обозначения… … Словарь-справочник терминов нормативно-технической документации

спектральная плотность мощности шума — spektrinis triukšmo galios tankis statusas T sritis radioelektronika atitikmenys: angl. noise spectral power density vok. Spektralleistungsdichte des Rauschens, f rus. спектральная плотность мощности шума, f pranc. densité spectrale de puissance… … Radioelektronikos terminų žodynas

спектральная плотность мощности излучения — spektrinis spinduliuotės galios tankis statusas T sritis Standartizacija ir metrologija apibrėžtis Pasirinktosios spektro dalies vienetinio dažnio, bangos ilgio (ar kito su jais susijusio dydžio) intervalo vidutinė spinduliuotės galios vertė.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

спектральная плотность мощности излучения — spektrinis spinduliuotės galios tankis statusas T sritis fizika atitikmenys: angl. radiation power spectral density vok. spektrale Strahlungsleistungsdichte, f rus. спектральная плотность мощности излучения, f pranc. densité spectrale de… … Fizikos terminų žodynas

относительная спектральная плотность мощности шума прибора СВЧ — Ндп. энергетический спектр шума энергетический спектр флуктуаций спектральная плотность шума ΔPш Отношение спектральной плотности мощности шума прибора СВЧ к выходной мощности в полосе 1 Гц. [ГОСТ 23769 79] Недопустимые, нерекомендуемые… … Справочник технического переводчика

Относительная спектральная плотность мощности шума прибора СВЧ — 222. Относительная спектральная плотность мощности шума прибора СВЧ Ндп. Энергетический спектр шума Энергетический спектр флуктуации Спектральная плотность шума Relative noise spectral power density ΔPш Отношение спектральной плотности мощности… … Словарь-справочник терминов нормативно-технической документации

Спектральная плотность — В статистической радиотехнике и физике при изучении детерминированных сигналов и случайных процессов широко используется их спектральное представление в виде спектральной плотности, которая базируется на преобразовании Фурье. Если процесс имеет… … Википедия

Спектральная плотность излучения — характеристика спектра излучения, равная отношению интенсивности (плотности потока) излучения в узком частотном интервале к величине этого интервала. Является применением понятия спектральной плотности мощности к электромагнитному излучению.… … Википедия

Спектральная плотность энергии (мощности) лазерного излучения — 5. Спектральная плотность энергии (мощности) лазерного излучения* Спектральная плотность энергии (мощности) СПЭ (СПМ) Wλ, Wv, Pλ, Pv Источник … Словарь-справочник терминов нормативно-технической документации

Источник

Что такое спектральная плотность сигнала

В статистической радиотехнике и физике при изучении детерминированных сигналов и случайных процессов широко используется их спектральное представление в виде спектральной плотности, которая базируется на преобразовании Фурье.

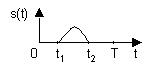
потом мы находим s(t) с помощью разложения п ряду Фурье бляяяяяя и затем в пределе получаем

Пределы интегрирования можно для общности поставить бесконечными, так как все равно там, где s(t) равна нулю, и интеграл равен нулю.

Выражение для спектральной плотности называют прямым преобразованием Фурье. Обратное преобразование Фурье определяет временную функцию сигнала по его спектральной плотности:

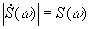Прямое (*) и обратное (**) преобразования Фурье вместе называют парой преобразований Фурье. Модуль спектральной плотности
определяет амплитудно-частотную характеристику (АЧХ) сигнала, а ее аргумент

7. Применение БПФ для моделирования искажений сигналов в линейных цепях

Линейная цепь – состоит из линейных элементов (емкость, сопротивление)

Сопротивление – элемент, который энергию превращает в тепло.

В механике аналогией конденсатору служит пружина(элемент,который запасает энергию).

Ток течет через конденсатор, когда меняется напряжение. Чем больше скорость изменения напряжения, тем больше ток.

Самый простой сигнал: последовательность прямоугольных импульсов. Искажение наиболее просто выявить, так, как прямоугольный сигнал имеет крутые фронты.

Если пропустить сигнал прямоугольных импульсов,через простейшую Rc цепочку(фильрр низких частот),то спектр этого сигнала исказится,так,как фильтр не пропускает импульсы на больших частотах.

Активными элементами считаются источники электрической энергии (источники напряжения и тока), к пассивным элементам относятся резисторы, катушки индуктивности, электрические конденсаторы.

Количественные характеристики элементов электрической цепи называются ее параметрами.

Если сопротивление резистора R не зависит от тока, то линейная зависимость между падением напряжения и током выражается законом Ома ur = R х ir, а вольт-амперная характеристика резистора (представляет собой прямую линию (рис. 1,а).

Если индуктивность катушки не зависит от величины (протекающего в ней тока, то потокосцепление самоиндукции катушки ψ прямо пропорционально этому току ψ= L х il (рис. 1,б).

Наконец, если емкость конденсатора С не зависитот приложенного к обкладкам напряжения uc то заряд q, накопленный на пластинах, и напряжение uc связаны между собой линейной зависимостью графически показанной на рис. 1,в.

Линейность сопротивления, индуктивности и емкости носит условный характер, так как в действительности все реальные элементы электрической цепи являются нелинейными. Так, при прохождении тока через резистор последний нагревается и его сопротивление изменяется.

Электрическая цепь, состоящая из линейных элементов, называется линейной электрической цепью. Процессы в таких цепях описываются линейными алгебраическими или дифференциальными уравнениями. Для анализа процессов в линейных электрических цепях используются законы Кирхгофа.

! Писала, то что запомнила с сегодняшней консультации и с лекций

8. Применение БПФ для фильтрации сигналов

Рисунок 19 иллюстрирует технику фильтрации с применением БПФ. Сначала синтезируется исходный сигнал, представленный 128 отсчетами вектора v. Затем к этому сигналу присоединяется шум с помощью генератора случайных чисел (функция rnd) и формируется вектор из 128 отсчетов зашумленного сигнала.

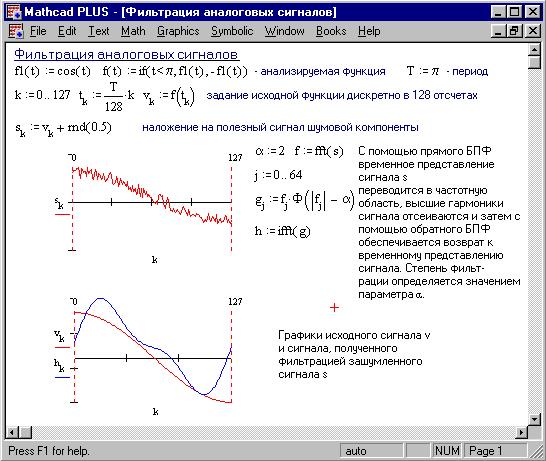
Рисунок 19. Фильтрация аналоговых сигналов

Ф(х) Ступенчатая функция Хевисайда. Возвращает 1, если х >= 0; иначе 0.

Отфильтрованный сигнал (вектор g) подвергается обратному БПФ и создает вектор выходного сигнала h.

Сравнение временных зависимостей исходного и выходного сигналов, показывает, что выходной сигнал почти полностью повторяет входной и в значительной мере избавлен от высокочастотных шумовых помех, маскирующих полезный сигнал.

9. Аналогии цепей различной физической природы;

До создания цифровых электронных вычислительных машин в конце 1940-х гг. Моделирование аналоговое было основным способом «предметно-математического моделирования» (см. об этом в ст. Моделирование) многих процессов, связанных с распространением электромагнитных и звуковых волн, диффузии газов и жидкостей, движения и фильтрации жидкостей в пористых средах, кручения стержней и др. (в связи с чем его часто называли тогда просто «математическим моделированием»), причём для каждой конкретной задачи моделирования строилась своя «сеточная» модель (основными её элементами служили соединённые в плоскую сеточную схему электрические сопротивления различных видов), а аналоговые вычислительные машины позволяли проводить Моделирование аналоговое целых классов однородных задач. В настоящее время значение Моделирование аналоговое значительно уменьшилось, поскольку моделирование на ЭВМ имеет большие преимущества перед ним в отношении точности моделирования и универсальности. В достаточно фиксированных и специальных задачах свои преимущества (простота, а тем самым и дешевизна технического выполнения) имеет и Моделирование аналоговое Употребительно также и совместное использование обоих методов (см. Гибридная вычислительная система).

10. Математические модели накопителей потенциальной и кинетической энергии;

Потенциальная энергия 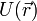— скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил

Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.

Источник