в чем измеряется скорость звука в воздухе

Скорость звука и число М

Для начала давайте выясним, сверхзвук — это сколько км/ч? Какова должна быть скорость, чтобы считаться сверхзвуковой? Проблема в том, что простого и однозначного ответа на этот вопрос… Просто нет.

Есть правильный ответ — больше 1 М. Или Число Маха равное единице, это скорость звука, а выше единицы, это уже сверхзвук.

Совсем не привычное нам число, выраженное в километрах в час. Если упростить, то объяснить можно так: скорость звука зависит о свойств среды в которой он распространяется, чем плотнее среда, тем быстрее распространяются колебания (звук это ведь волна). Таким образом на разной высоте скорость звука разная. Чем выше, тем меньше плотность воздуха и тем ниже будет местная скорость звука.

Что такое скорость звука

Скорость звука в километрах в час не выражается, просто потому, что в таком случае она всегда будет разной.

Зависимость скорости звука от высоты полета

Например, скорость звука у земли (на высоте 0 км) составит 340 метров в секунду (м/с), это 1224 км/ч. И тут важно сказать что такое значение будет: при температуре +15 и давлении 750 мм. рт. ст. и относительной влажности 0%. То есть, при «стандартных» условиях.

А вот на высоте 10 000 метров, на которой летают современные пассажирские лайнеры, это уже около 299 м/с (это 1076 км/ч), то есть разница довольно значительная — 12%.

Также от высоты полета и других параметров атмосферы зависит и скорость звука, и сопротивление воздуха и, соответственно, скорость самолета, которую он может развить.

Скорость звука на высоте 11 километров и выше почти не будет меняться, эта часть атмосферы называется «тропопауза».

То же самое в виде таблицы

Зависимость скорости звука от высоты*

Высота, м	Скорость звука, м/с	Скорость звука, км/ч
-1000	344,1	1 238,8
0	340,3	1 225,1
1000	336,4	1 211,0
2000	332,5	1 197,0
3000	328,6	1 183,0
4000	324,6	1 168,6
5000	320,6	1 154,2
6000	316,5	1 139,4
7000	312,3	1 124,3
8000	308,1	1 109,2
9000	303,9	1 094,0
10000	299,6	1 078,6
11000	295,2	1 062,7
12000	295,1	1 062,4
13000	295,1	1 062,4
14000	295,1	1 062,4

*Минутка занудства. Нужно напомнить, что на самом деле скорости звука от высоты зависит условно, это упрощение. Скорость звука зависит от плотности атмосферы, а плотность воздуха, в свою очередь, зависит от температуры, влажности и давления, которые меняются с высотой.

Зачем нужно число Маха

Так вот, число Маха в авиации представляет собой отношение скорости летательного аппарата к скорости звука на той высоте на которой он сейчас летит. Так удобнее, ведь на разной высоте скорость звука будет разной и чтобы понимать достигает ли самолет скорости звука, его скорость измеряют в числах М.

Один мах, это просто — 1 мах, а не «км/ч». Нельзя просто ответить на вопрос «сколько 1 мах в километрах в час», нужно всегда уточнять, о какой высоте идет речь.

Если еще проще, число М показывает сколько скоростей звука в скорости самолета сейчас на конкретной высоте (при определенных условиях среды). Если число Маха больше единицы, очевидно, мы имеем дело со сверхзвуковой скоростью. Поэтому чаще всего вы будете встречать пояснение для какой высоты указано конкретное число Маха.

Например, для Боинга 777 крейсерской скоростью считается 0,84 М (это дозвуковой летательный аппарат). То есть на высоте 10 000 метров при стандартных условиях, принимая скорость звука за 1076 км/ч умножаем ее на 0,84 и получаем — 904 км/ч. По документации крейсерская скорость Boeing 777 составляет как раз 905 км/ч.

Что касается сверхзвуковых летательных аппаратов, то, по определению, их скорости должны быть больше скорости звука, то есть больше 1 М. Например у Су-27 это 2,35 М, что примерно 2 528 км/ч на высоте 10 км (скорость звука 295 м/с, а это 1062 км/ч).

Число М некоторых сверхзвуковых самолетов:

А вот гиперзвуковые летательные аппараты:

SR-71 — самый быстрый серийный самолет

Еще одно замечание, число Маха в авиации, это качественная величина, а не количественная. То есть это не скорость в чистом виде, а критерий который показывает насколько скорость объекта выше скорости звука. Зачем? Затем, что дозвуковые, трансзвуковые, сверхзвуковые или гиперзвуковые скорости очень сильно отличаются по сути.

Пилоту (и инженеру тоже) важно знать какой у него сейчас режим обтекания самолета (дозвуковой, трансзвуковой или сверхзвуковой). Например, во многих указателях скорости есть отдельный циферблат, показывающий значение числа Маха в дополнению к приборной скорости.

На картинке в начале этого повествования изображен трансзвуковой режим. Это значит, что сам самолет еще не превысил скорость звука, а на некоторых его участках (на фото это очень хорошо видно по белым «клиньям») скорость обтекания уже достигла скорости звука.

Поэтому и образовались скачки уплотнения которые хорошо видны благодаря образованию конденсата позади них. Вот почему, число Маха так важно.

Источник

Скорость звука

Из Википедии — свободной энциклопедии

Скорость звука в различных средах [1]

0 °C, 101325 Па	м/с	км/ч
Азот	334	1202,4
Аммиак	415	1494,0
Ацетилен	327	1177,2
Водород	1284	4622,4
Воздух	331	1191,6
Гелий	965	3474,0
Кислород	316	1137,6
Метан	430	1548,0
Угарный газ	338	1216,8
Неон	435	1566,0
Углекислый газ	259	932,4
Хлор	206	741,6
Жидкости
Вода	1403	5050,8
Ртуть	1383	4978,0
Твёрдые тела
Алмаз	12000	43200,0
Железо	5950	21420,0
Золото	3240	11664,0
Литий	6000	21600,0
Стекло	4800	17280,0

Скорость звука — скорость распространения упругих волн в среде: как продольных (в газах, жидкостях или твёрдых телах), так и поперечных, сдвиговых (в твёрдых телах).

Определяется упругостью и плотностью среды: как правило, в газах скорость звука меньше, чем в жидкостях, а в жидкостях — меньше, чем в твёрдых телах. Также в газах скорость звука зависит от температуры данного вещества, в монокристаллах — от направления распространения волны.

Обычно не зависит от частоты волны и её амплитуды; в тех случаях, когда скорость звука зависит от частоты, говорят о дисперсии звука.

Источник

Звук (звуковые волны). Скорость звука.

Для распространения звука необходима упругая среда. В вакууме звуковые волны распро­страняться не могут, так как там нечему колебаться. В этом можно убедиться на простом опыте. Если поместить под стеклянный колокол электрический звонок, то по мере выкачивания из-под колокола воздуха звук от звонка будет становиться все слабее и слабее, пока не прекратится совсем.

Известно, что во время грозы мы видим вспышку молнии и лишь через некоторое время слы­шим раскаты грома. Это запаздывание возникает из-за того, что скорость звука в воздухе значи­тельно меньше скорости света, идущего от молнии.

Скорость звука в воздухе впервые была измерена в 1636 г. французским ученым М. Мерсенном. При температуре 20 °С она равна 343 м/с, т. е. 1235 км/ч. Заметим, что именно до такого значения уменьшается на расстоянии 800 м скорость пули, вылетевшей из автомата Калашни­кова. Начальная скорость пули 825 м/с, что значительно превышает скорость звука в воздухе. Поэтому человек, услышавший звук выстрела или свист пули, может не беспокоиться: эта пуля его уже миновала. Пуля обгоняет звук выстрела и достигает своей жертвы до того, как приходит этот звук.

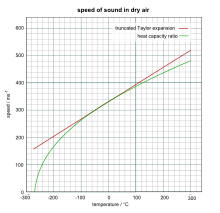
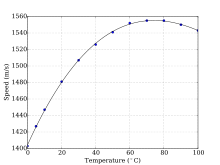
Скорость звука в газах зависит от температуры среды: с увеличением температуры воздуха она возрастает, а с уменьшением — убывает. При 0 °С скорость звука в воздухе составляет 332 м/с.

В разных газах звук распространяется с разной скоростью. Чем больше масса молекул газа, тем меньше скорость звука в нем. Так, при температуре 0 °С скорость звука в водороде составляет 1284 м/с, в гелии — 965 м/с, а в кислороде — 316 м/с.

Скорость звука в твердых телах больше, чем в жидкостях и газах. Если приложить ухо к рель­су, то после удара по другому концу рельса слышно два звука. Один из них достигает уха по рельсу, другой — по воздуху.

Хорошей проводимостью звука обладает земля. Поэтому в старые времена при осаде в крепос­тных стенах помещали «слухачей», которые по звуку, передаваемому землей, могли определить, ведет ли враг подкоп к стенам или нет. Прикладывая ухо к земле, также следили за приближе­нием вражеской конницы.

Твердые тела хорошо проводят звук. Благодаря этому люди, потерявшие слух, иной раз спо­собны танцевать под музыку, которая доходит до слуховых нервов не через воздух и наружное ухо, а через пол и кости.

Скорость звука можно определить, зная длину волны и частоту (или период) колебаний:

Источник

Скорость звука: каков ее предел?

Одна из основных задач какой-либо точной науки заключается в измерении и объяснении тех или иных процессов, а также их участников. За многие годы исследований, расчетов и споров научное сообщество пришло к пониманию того, что существуют определенные ограничения в некоторых явлениях. К примеру, скорость света в вакууме равна 299 792 458 м/с. Согласно специальной теории относительности, ничто не может двигаться быстрее. Другими словами, мы имеем верхний скоростной лимит для света. Однако такой лимит для скорости звука пока не был установлен. Ученые из Лондонского университета королевы Марии (Англия, Великобритания) провели расчеты, результатом которых стало открытие верхнего предела скорости звука. Что стало основой расчетов, каковы их результаты, и в каких областях можно применить новообретенные знания? Ответы на эти вопросы мы найдем в докладе ученых. Поехали.

Основа исследования

Звук это волны механических колебаний в какой-либо среде. Скорость распространения этих волн напрямую зависит от самой среды. К примеру, в твердых объектах звук распространяется быстрее, чем в воздухе. Однако и тут могут быть флуктуации в измерениях, поскольку важна не только среда как таковая, но и ее состояние (температура, давление и т.д.).

Логично, что скорость звука сложно назвать константой, так как в разных условиях она будет своя: в воздухе это 331 м/с, в воде 1500 м/с (тут будут вариации в зависимости от температуры, давления и солености воды), а в стекле 4800 м/с.

Но как же рассчитать верхний лимит скорости звука?

Как напоминают нам ученые, некоторые важные свойства конденсированных фаз* определяются фундаментальными физическими константами.

Конденсированные фазы* — состояние вещества, когда число его компонентов (атомов, молекул и т.д.) крайне велико, а взаимодействия между компонентами очень сильны. К числу таких фаз можно отнести и твердые вещества, и жидкости.

Постоянная Ридберга* — предельное значение наивысшего волнового числа любого фотона, который может быть испущен атомом водорода. Также эта постоянная определяет волновое число фотона с наименьшей энергией, способного ионизировать атом водорода в его основном состоянии.

Постоянная тонкой структуры* (⍺) — фундаментальная физическая постоянная, которая характеризует силу электромагнитного взаимодействия. Эта постоянная определяет размер крайне малого изменения величины энергетических уровней атома и образования тонкой структуры, которые являются набором узких и близких частот в его спектральных линиях.

Отношение массы протона к массе электрона* (m_p/m_e — константа, равная 1836,15267261.

Объединение этих констант позволяет определить новую безразмерную константу, описывающую верхнюю границу скорости звука (v_u) в конденсированных фазах (формула №1):

где c — скорость света в вакууме, ⍺ — постоянная тонкой структуры, m_p/m_e — отношение масс протона и электрона, v_u — верхний предел скорости звука.

Подтверждение верности данной формулы было получено благодаря многочисленным экспериментам и моделированию атомарного водорода.

Результаты исследования

Авторы сего труда отмечают, что существует два подхода к определению v (скорости звука). Один поход начинается с оценки упругости системы, а второй — с оценки ее вибрационных свойств. Оба подхода дают сопоставимые результаты (приготовьтесь, формул будет немало).

Используя E = E_R из формулы №3 в формуле №2 мы получим (формула №4):

где ⍺ = (1/4πϵ₀)(e 2 /hc) — постоянная тонкой структуры.

Такой же результат, как и в формуле №4, можно получить и посредством второго подхода, где основной акцент поставлен на рассмотрении вибрационных свойств системы.

Далее выбранный подход был проверен на более практическом уровне.

m_e характеризует электроны, которые отвечают за взаимодействия между атомами. Электронный вклад далее отражается в коэффициенте ⍺c (⍺c ∝ e 2 /h), который представляет собой скорость электронов в модели Бора. Ученые отмечают, что ⍺с и v не зависят от c. Использование формулировки v в виде ⍺с в формуле №4 обусловлено двумя факторами.

Во-первых, так намного удобнее и информативнее представлять границу в отношении v_u/c, что обычно применяется в отношении скорости Ферми и скорости света (v_F/c).

Во-вторых, именно ⍺ (наряду с m_p/m_e) имеет фундаментальное для стабильности протонов и обеспечения синтеза тяжелых элементов и, следовательно, существования твердых тел и жидкостей, в которых звук может распространяться.

m формула №4 характеризует атомы, участвующие в распространении звука. Его масштаб задается массой протона m_p: m = Am_p, где A — атомная масса. Учитывая, что А = 1, а m = m_p, применение формулы №4 позволяет определить значение верхней границы скорости звука (формула №9):

Таким образом было показано, что v_u зависит только от фундаментальных физических констант, включая безразмерную постоянную тонкой структуры и отношение масс протона и электрона.

Вышеуказанная формула является расширенным вариантом формулы №4 для атомарного водорода. Объединение формул №4 и №9, при учете m = Am_p, позволяет получить (формула №10):

Что ж, теперь можно немного отдохнуть от формул и приступить к обсуждению расчетов и экспериментов.

Ученые отмечают, что хоть скорость звука определяется модулями упругости и плотностью, они существенно отличаются в зависимости от типа связи: сильные ковалентная, ионная или металлическая связи, обычно дающей большую энергию связи, промежуточные водородные связи, а также слабые дипольные и ван-дер-ваальсовые взаимодействиям. Модули упругости и плотность также меняются в зависимости от конкретной конструкции, которую принимает система. Кроме того, тип связи и структура сами по себе взаимозависимы: ковалентная связь приводят к образованию открытых структур, а ионная — плотноупакованных. Следовательно, скорость звука для конкретной системы не может быть предсказана аналитически и без явного знания структуры и взаимодействий внутри нее, подобно другим системно-зависимым свойствам, таким как вязкость или теплопроводность.

Тем не менее зависимость v от m или A может быть изучена в семействе элементарных твердых тел. Элементарные твердые вещества не имеют смешанных особенностей, существующих в соединениях из-за смешанной связи между разными атомными разновидностями (включая смешанную ковалентно-ионную связь между одними и теми же парами атомов, а также разные типы связи между разными парами).

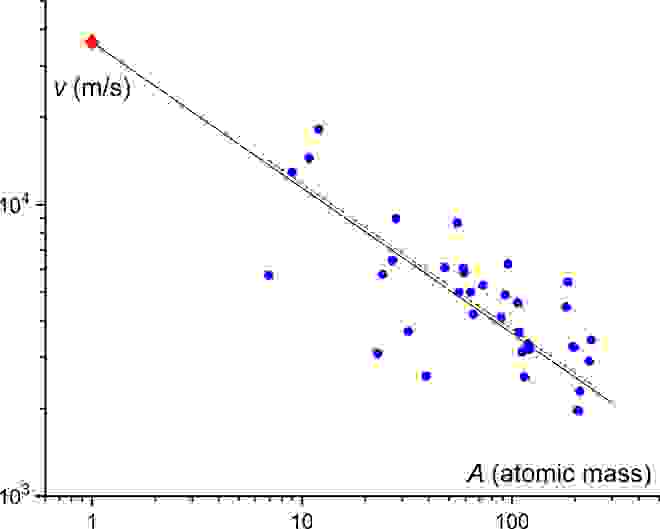
Изображение №1

Коэффициент корреляции Пирсона* используется для изучения связи двух переменных, измеренных в метрических шкалах на одной и той же выборке.

Расчетные и экспериментальные значения v_u, показанные на графике прямой и пунктирной линиями, указывают на пересечение в точке 37.350 м/с, что подтверждает верность расчетных походов и, особенно, верность аппроксимации коэффициент в формуле №4, что дает хорошее согласование с экспериментальными данными.

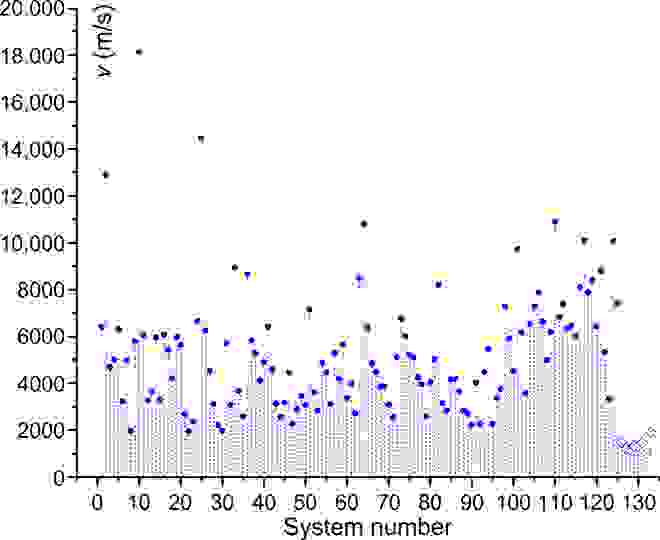
Изображение №2

Далее было решено проверить согласование расчетных данных с экспериментальными с применением более широкого спектра образцов (133 образца). Экспериментальные значения v были меньше, чем верхняя теоретическая граница v_u в формуле №9. v_u примерно вдвое больше v в алмазе, это является самой высокой скоростью звука, измеренной в условиях окружающей среды.

Формула №10 может использоваться для приблизительного прогнозирования средней или характеристической скорости звука (v). A1/2, которая, согласно формуле №10, относится к скорости звука, варьируется по периодической таблице в диапазоне от 1 до 15 со средним значением 8. Согласно расчетам соответствующее значение v равно 4513 м/с. Это на 16% согласуется с 5392 м/с — средним значением по всем элементарным твердым телам, и на 14% с 5267 м/с — средним значением по всем твердым телам на графике выше.

В эксперименты также были включены данные по скорости звука в жидкости при комнатной температуре, которые варьируются от 1000 до 2000 м/с. Однако в высокотемпературных жидких металлах, таких как Al, Fe, Mg и Ni, v достигает более высоких значений в диапазоне от 4000 до 5000 м/с. Из этого следует, что скорость звука в жидкостях полностью удовлетворяет расчетную верхнюю границу скорости.

Ученые отмечают, что хоть приближения, использованные в некоторых формулах, и могут повлиять на вычисление v и его оценку, v_u все же формируется исходя из фундаментальных констант. Другими словами, в конечном итоге приближения не имеют столь значимого влияния.

Также было установлено, что рассчитанное значение верхней границы скорости звука применимо к твердым телам не только с сильной межатомной связью, но и со слабой. Формула №3, 6 и 7 предполагают, что валентные электроны непосредственно участвуют в связывании. Следовательно, они играют важную роль в системах с металлической, ковалентной и ионной связью. Несмотря на то, что связывание в твердых телах со слабой связью также имеет электромагнитное происхождение, слабые дипольные и ван-дер-ваальсовые взаимодействия приводят к меньшему E и, как результат, меньшему v. Потому из этого следует, что верхняя граница v_u применима и к слабосвязанным системам.

Ученые отмечают, что верхняя граница v_u соответствует твердому водороду с прочной металлической связью. Данная фаза вещества существует только при мегабарном давлении и динамически нестабильна при атмосферном давлении, где происходит образование молекул. Посему было решено провести расчеты v в атомарном водороде, чтобы подтвердить верность расчетов как таковых.

Расчеты скорость звука в атомарном водороде проводились с применением структуры I4₁/amd, которая является наилучшей структурой-образцом для твердого атомарного металлического водорода. Известно, что эта структура становится термодинамически стабильной в диапазоне давлений от 400 до 500 ГПа, ниже которого твердый водород является молекулярным твердым телом. Однако было обнаружено, что I4₁/amd динамически устойчива при давлениях выше примерно 250 ГПа, поэтому расчеты проводились в диапазоне давления от 250 до 1000 ГПа.

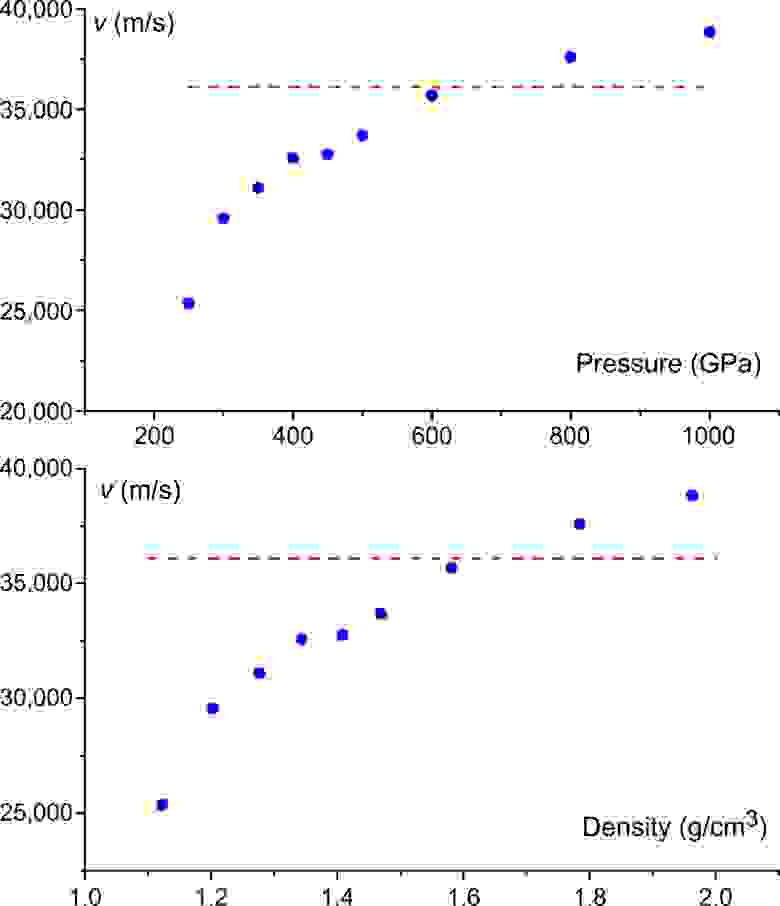
Изображение №3

На графике выше представлена скорость звука как функция давления и плотности. Рассчитанное значение скорости звука было ниже значения v_u в широком диапазоне давлений. Увеличение v выше расчетной верхней границы возникает лишь при давлении 600 ГПа и выше. Следовательно, при нормальных условиях скорость звука не будет превышать расчетную верхнюю границу.

Для более подробного ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых.

Эпилог

В данном труде ученые определили, что важнейшую роль в оценке максимально возможной скорости звука играют две фундаментальные константы — постоянная тонкой структуры и отношение массы протона к массе электрона.

Проведенные расчеты были проверены на практике с применением разнообразных материалов. Эксперименты позволили установить, что скорость звука должна уменьшаться с атомарной массой. Из этого следует, что максимальная скорость звука достигается в твердом атомарном водороде, который может существовать в таком виде лишь при очень высоком давлении. Тем не менее было установлено, что верхняя граница скорости звука в рамках данного исследования составляет 36100 м/с. С практической точки зрения, подобные исследования крайне важны для понимания тех или иных материалов, а также их свойств.

Естественно, ученые не намерены останавливаться на достигнутом. Их расчеты и соответствующие экспериментальные данные требуют перепроверки, уточнения и дополнительного подтверждения. В будущем данное исследование будет продолжено, а верхняя граница скорости звука может неожиданно сместиться в большую или меньшую сторону ввиду новых данных. Как бы то ни было, фундаментальный подход остается прежним, а сам факт лучшего понимания процессов, протекающих вокруг нас, позволяет с уверенностью смотреть на развитие данного исследования.

Благодарю за внимание, оставайтесь любопытствующими и хорошей всем рабочей недели, ребята. 🙂

Немного рекламы

Источник

Скорость звука в идеальном газе зависит только от его температуры и состава. Скорость имеет слабую зависимость от частоты и давления в обычном воздухе, немного отклоняясь от идеального поведения.

СОДЕРЖАНИЕ

История

Базовые концепты

Передачу звука можно проиллюстрировать с помощью модели, состоящей из массива сферических объектов, связанных между собой пружинами.

Скорость звука в модели зависит от жесткости / жесткости пружины и массы сфер. Пока расстояние между сферами остается постоянным, более жесткие пружины / связи передают энергию быстрее, в то время как более крупные сферы передают энергию медленнее.

Например, звук в никеле распространяется в 1,59 раза быстрее, чем в бронзе, из-за большей жесткости никеля примерно при такой же плотности. Точно так же звук распространяется примерно в 1,41 раза быстрее в газе легкого водорода ( протия ), чем в газе тяжелого водорода ( дейтерия ), поскольку дейтерий имеет аналогичные свойства, но в два раза большую плотность. В то же время звук «компрессионного типа» будет распространяться быстрее в твердых телах, чем в жидкостях, и быстрее в жидкостях, чем в газах, потому что твердые тела сложнее сжимать, чем жидкости, а жидкости, в свою очередь, труднее сжимать. чем газы.

В некоторых учебниках ошибочно утверждается, что скорость звука увеличивается с плотностью. Это понятие проиллюстрировано представлением данных для трех материалов, таких как воздух, вода и сталь, каждый из которых имеет существенно разную сжимаемость, что более чем компенсирует разницу в плотности. Наглядным примером этих двух эффектов является то, что звук в воде распространяется всего в 4,3 раза быстрее, чем в воздухе, несмотря на огромные различия в сжимаемости двух сред. Причина в том, что большая плотность воды, которая замедляет звук в воде по сравнению с воздухом, почти компенсирует разницу в сжимаемости двух сред.

Практический пример можно наблюдать в Эдинбурге, когда «One o’Clock Gun» стреляет в восточном конце Эдинбургского замка. Стоя у подножия западной оконечности Касл-Рока, звук ружья можно услышать сквозь скалу, незадолго до того, как он прибудет по воздуху, частично задержанный немного более длинным маршрутом. Это особенно эффективно, если производится салют из нескольких пистолетов, например, «День рождения королевы».

Сжатие и поперечные волны

Уравнения

Для жидкостей в целом скорость звука c определяется уравнением Ньютона – Лапласа:

Зависимость от свойств среды

В газах адиабатическая сжимаемость напрямую связана с давлением через коэффициент теплоемкости (показатель адиабаты), в то время как давление и плотность обратно пропорциональны температуре и молекулярной массе, поэтому важны только полностью независимые свойства температуры и молекулярной структуры (теплоемкость соотношение может определяться температурой и молекулярной структурой, но простой молекулярной массы недостаточно для ее определения).

Изменение высоты и последствия для атмосферной акустики

Практическая формула для сухого воздуха

Приблизительную скорость звука в сухом (влажность 0%) воздухе в метрах в секунду при температуре около 0 ° C можно рассчитать по формуле

\ mathrm <м / с>,>

Это уравнение получено из первых двух членов разложения Тейлора следующего более точного уравнения:

\ mathrm .>

Разделив первую часть и умножив вторую часть справа на √ 273,15, мы получим точно эквивалентную форму

\ mathrm .>

который также можно записать как

\ mathrm <м / с>>

Подробности

Скорость звука в идеальных газах и воздухе

Для идеального газа K ( объемный модуль упругости в уравнениях выше, эквивалентный C, коэффициент жесткости в твердых телах) определяется выражением

таким образом, из приведенного выше уравнения Ньютона – Лапласа скорость звука в идеальном газе определяется выражением

Это уравнение применяется только в том случае, если звуковая волна представляет собой небольшое возмущение окружающих условий, и выполняются некоторые другие отмеченные условия, как указано ниже. Расчетные значения c _воздух незначительно отличаются от экспериментально определенных значений.

Численная подстановка приведенных выше значений дает приближение скорости звука для газов в идеальном газе, которое является точным при относительно низких давлениях и плотностях газа (для воздуха это включает стандартные условия на уровне Земли на уровне моря). Кроме того, для двухатомных газов использование γ = 1,4000 требует, чтобы газ существовал в достаточно высоком температурном диапазоне, чтобы вращательная теплоемкость была полностью возбуждена (т.е. вращение молекул полностью использовалось в качестве «перегородки» или резервуара тепловой энергии); но в то же время температура должна быть достаточно низкой, чтобы молекулярные колебательные моды не вносили вклад в теплоемкость (т. е. незначительное тепло переходит в вибрацию, так как все колебательные квантовые моды выше моды минимальной энергии имеют слишком высокие энергии, чтобы их мог заселить значительное количество молекул при этой температуре). Для воздуха эти условия выполняются при комнатной температуре, а также при температурах значительно ниже комнатной (см. Таблицы ниже). См. Раздел, посвященный газам в удельной теплоемкости, для более полного обсуждения этого явления.

Для воздуха мы вводим сокращение

Подстановка числовых значений

р знак равно 8,314 463 J / ( м о л ⋅ K ) <\ Displaystyle R = 8,314 \, 463

\ mathrm >

для молярной газовой постоянной в Дж / моль / Кельвин, и

M а я р знак равно 0,028 964 5 k грамм / м о л <\ displaystyle M _ <\ mathrm > = 0,028 \, 964 \, 5

\ mathrm <кг / моль>>

\ mathrm .>

\ mathrm .>

Приведенный выше вывод включает первые два уравнения, приведенные в разделе «Практическая формула для сухого воздуха» выше.

Воздействие сдвига ветра

Для распространения звука экспоненциальное изменение скорости ветра с высотой можно определить следующим образом:

В битве при Юке в ходе Гражданской войны в США в 1862 году акустическая тень, которая, как считается, была усилена северо-восточным ветром, не позволила двум дивизиям солдат Союза участвовать в битве, поскольку они не могли слышать звуки боя всего в 10 км (шесть миль). ) по ветру.

Таблицы

Звуковые измерения

Влияние температуры на свойства воздуха

Температура, T ( ° C )	Скорость звука, ц ( м / с )	Плотность воздуха, ρ ( кг / м 3 )	Характеристический удельный акустический импеданс, z 0 ( Па · с / м )
35 год	351,88	1,1455	403,2
30	349,02	1,1644	406,5
25	346,13	1,1839	409,4
20	343,21	1,2041	413,3
15	340,27	1,2250	416,9
10	337,31	1,2466	420,5
5	334,32	1,2690	424,3
0	331,30	1,2922	428,0
−5	328,25	1,3163	432,1
−10	325,18	1,3413	436,1
−15	322,07	1,3673	440,3
−20	318,94	1,3943	444,6
−25	315,77	1,4224	449,1

При нормальных атмосферных условиях температура и, следовательно, скорость звука зависят от высоты:

Влияние частоты и состава газа

Общие физические соображения

Среда, в которой распространяется звуковая волна, не всегда реагирует адиабатически, и в результате скорость звука может изменяться с частотой.

Обратите внимание, что в этом примере мы предположили, что температура достаточно низкая, чтобы на теплоемкость не влияла молекулярная вибрация (см. Теплоемкость ). Однако колебательные моды просто вызывают гаммы, которые уменьшаются до 1, поскольку колебательные моды в многоатомном газе дают газу дополнительные способы хранения тепла, которые не влияют на температуру и, таким образом, не влияют на скорость молекул и скорость звука. Таким образом, эффект более высоких температур и колебательной теплоемкости увеличивает разницу между скоростью звука в одноатомных и многоатомных молекулах, при этом скорость остается большей в одноатомных.

Практическое применение в воздухе

Безусловно, наиболее важным фактором, влияющим на скорость звука в воздухе, является температура. Скорость пропорциональна квадратному корню из абсолютной температуры, что дает увеличение примерно на 0,6 м / с на градус Цельсия. По этой причине высота звука музыкального духового инструмента увеличивается с повышением его температуры.

Скорость звука увеличивается из-за влажности. Разница между влажностью 0% и 100% составляет около 1,5 м / с при стандартном давлении и температуре, но величина эффекта влажности резко возрастает с температурой.

число Маха

Число Маха, полезная величина в аэродинамике, представляет собой отношение скорости воздуха к локальной скорости звука. На высоте по объясненным причинам число Маха является функцией температуры.

Однако летные приборы самолета работают с использованием перепада давления для вычисления числа Маха, а не температуры. Предполагается, что конкретное давление представляет собой конкретную высоту и, следовательно, стандартную температуру. Летательные приборы самолета должны работать таким образом, потому что давление торможения, измеряемое трубкой Пито, зависит как от высоты, так и от скорости.

Экспериментальные методы

Существует ряд различных методов измерения звука в воздухе.

Методы однократного отсчета времени

Если источник звука и два микрофона расположены по прямой линии с источником звука на одном конце, то можно измерить следующее:

Другие методы

В этих методах, то время измерение было заменено измерением обратного времени ( частоты ).

Высокоточные измерения в воздухе

Негазообразные среды

Скорость звука в твердых телах

Трехмерные твердые тела

В твердом теле существует ненулевая жесткость как для объемных деформаций, так и для деформаций сдвига. Следовательно, можно генерировать звуковые волны с разными скоростями в зависимости от режима деформации. Звуковые волны, вызывающие объемные деформации (сжатие) и сдвиговые деформации (сдвиг), называются волнами давления (продольными волнами) и поперечными волнами (поперечными волнами) соответственно. При землетрясениях соответствующие сейсмические волны называются P-волнами (первичными волнами) и S-волнами (вторичными волнами) соответственно. Скорости звука этих двух типов волн, распространяющихся в однородном трехмерном твердом теле, соответственно определяются выражением

Одномерные твердые тела

Скорость звука для волн давления в жестких материалах, таких как металлы, иногда указывается для «длинных стержней» рассматриваемого материала, скорость в которых легче измерить. В стержнях, диаметр которых меньше длины волны, скорость чистых волн давления может быть упрощена и определяется выражением:

Скорость звука в жидкостях

В жидкости единственная ненулевая жесткость связана с объемной деформацией (жидкость не выдерживает поперечных сил).

Следовательно, скорость звука в жидкости определяется выражением

Морская вода

4 м / с ) и солености (изменение 1 ‰

1 м / с ), и эмпирические уравнения были получены чтобы точно рассчитать скорость звука по этим переменным. Другие факторы, влияющие на скорость звука, незначительны. Поскольку в большинстве районов океана температура уменьшается с глубиной, профиль скорости звука с глубиной уменьшается до минимума на глубине нескольких сотен метров. Ниже минимума скорость звука снова увеличивается, поскольку эффект увеличения давления преодолевает эффект снижения температуры (справа). Для получения дополнительной информации см. Dushaw et al.

Эмпирическое уравнение для скорости звука в морской воде предоставлено Маккензи:

(Примечание: график зависимости скорости звука от глубины не коррелирует напрямую с формулой Маккензи. Это связано с тем, что температура и соленость различаются на разных глубинах. Когда T и S остаются постоянными, сама формула всегда увеличивается с глубина.)

Другие уравнения скорости звука в морской воде точны в широком диапазоне условий, но намного сложнее, например, уравнение В.А. Дель Гроссо и уравнение Чена-Миллеро-Ли.

Скорость звука в плазме

Скорость звука в плазме для общего случая, когда электроны горячее, чем ионы (но не намного горячее), задается формулой (см. Здесь )

\ mathrm <м / с>,>

В отличие от газа, давление и плотность определяются отдельными составляющими: давлением электронов и плотностью ионов. Они связаны через флуктуирующее электрическое поле.

Градиенты

Когда звук распространяется равномерно во всех направлениях в трех измерениях, его интенсивность падает пропорционально обратному квадрату расстояния. Однако в океане есть слой, называемый «глубокий звуковой канал» или канал SOFAR, который может удерживать звуковые волны на определенной глубине.

Аналогичный эффект происходит в атмосфере. Проект Могул успешно использовал этот эффект для обнаружения ядерного взрыва на значительном расстоянии.

Источник