Реактивное сопротивление в электротехнике

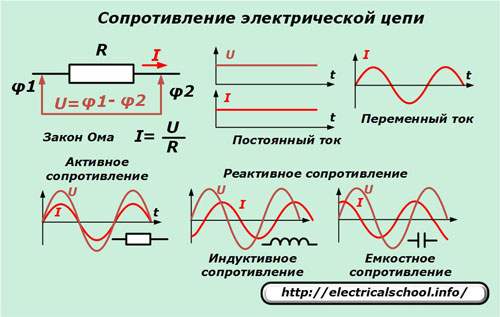
Известный в электротехнике закон Ома объясняет, что если по концам какого-то участка цепи приложить разность потенциалов, то под ее действием потечет электрический ток, сила которого зависит от сопротивления среды.

Источники переменного напряжения создают ток в подключенной к ним схеме, который может повторять форму синусоиды источника или быть сдвинутым по углу от него вперед либо назад.

Если электрическая цепь не изменяет направления прохождения тока и его вектор по фазе полностью совпадает с приложенным напряжением, то такой участок обладает чистым активным сопротивлением. Когда же наблюдается отличие во вращении векторов, то говорят о реактивном характере сопротивления.

Различные электротехнические элементы обладают неодинаковой способностью отклонять направление тока, протекающего через них и изменять его величину.

Реактивное сопротивление катушки

Возьмем источник стабилизированного переменного напряжения и отрезок длинной изолированной проволоки. Вначале подключим генератор на всю расправленную проволоку, а затем на ее же, но смотанную кольцами вокруг магнитопровода, который используется для улучшения прохождения магнитных потоков.

Точно замеряя в обоих случаях ток, можно заметить, что при втором эксперименте будет замечено значительное снижение его величины и отставание по фазе на определенный угол.

Это происходит за счет возникновения противодействующих сил индукции, проявляющихся под действием закона Ленца.

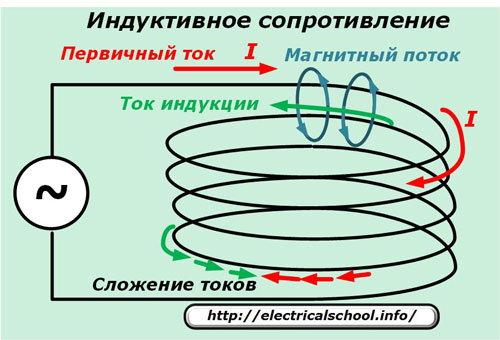
На рисунке прохождение первичного тока показано красными стрелками, а создаваемое им магнитное поле — синими. Направление его движения определяется по правилу правой руки. Оно же пересекает все соседние витки внутри обмотки и индуцирует в них ток, показанный зелеными стрелками, который ослабляет величину приложенного первичного тока, одновременно сдвигая его направление по отношению к приложенной ЭДС.

Чем большее число витков намотано на катушке, тем сильнее создается индуктивное сопротивление X_L, уменьшающее первичный ток.

Его величина зависит от частоты f, индуктивности L, рассчитывается по формуле:

За счет преодоления сил индуктивности ток на катушке отстает от напряжения на 90 градусов.

Реактивное сопротивление трансформатора

У этого устройства на общем магнитопроводе расположены две или большее количество обмоток. Одна из них получает электроэнергию от внешнего источника, а другим она передается по принципу трансформации.

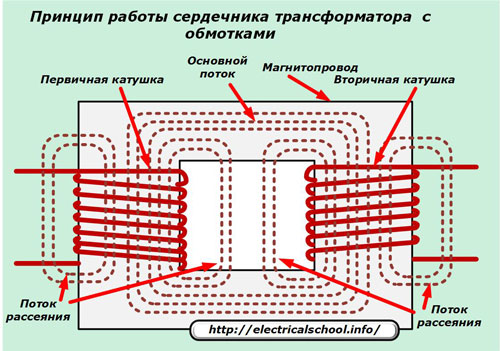
Первичный ток, проходящий по силовой катушке, наводит в магнитопроводе и вокруг него магнитный поток, который пересекает витки вторичной обмотки и формирует в ней вторичный ток.

Поскольку идеально создать конструкцию трансформатора невозможно, то часть магнитного потока будет рассеиваться в окружающую среду и создаст потери. Они называются потоком рассеивания и влияют на величину реактивного сопротивления рассеяния.

К ним добавляется активная составляющая сопротивления каждой обмотки. Полученная суммарная величина называется электрическим импедансом трансформатора или его комплексным сопротивлением Z, создающим перепады напряжения на всех обмотках.

Для математического выражения взаимосвязей внутри трансформатора активное сопротивление обмоток (обычно изготавливаемых из меди) обозначают индексами «R1» и «R2», а индуктивное — «Х1» и «Х2».

Импеданс в каждой обмотке имеет вид:

В этом выражении индексом «j» обозначена мнимая единица, расположенная на вертикальной оси комплексной плоскости.

Наиболее критичный режим в отношении индуктивного сопротивления и возникновении реактивной составляющей мощности создается при параллельном подключении трансформаторов в работу.

Реактивное сопротивление конденсатора

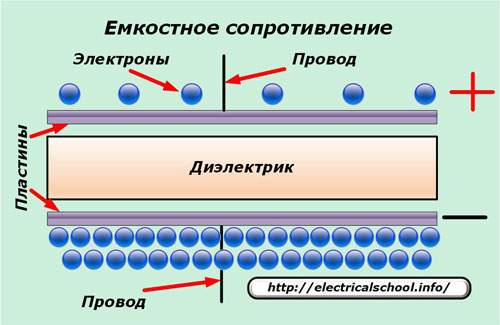
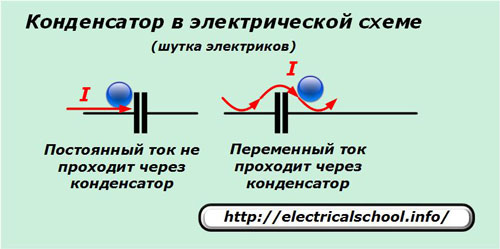
Конструктивно в его состав входят две или несколько токопроводящих пластин, отделенных слоем материала, обладающего диэлектрическими свойствами. За счет этого разделения постоянный ток не может пройти через конденсатор, а переменный — способен, но с отклонением от первоначальной величины.

Ее изменение объясняется принципом работы реактивного — емкостного сопротивления.

Под действием приложенного переменного напряжения, изменяющегося по синусоидальной форме, на обкладках происходит всплеск, накопление зарядов электрической энергии противоположных знаков. Общее их количество ограничено габаритами устройства и характеризуется емкостью. Чем она больше, тем дольше времени идет заряд.

В течение следующего полупериода колебания полярность напряжения на обкладках конденсатора меняется на противоположное. Под его воздействием происходит смена потенциалов, перезарядка сформированных зарядов пластин. Таким способом создается протекание первичного тока и противодействие его прохождению, когда он уменьшается по величине и сдвигается по углу.

По этому вопросу у электриков есть шутка. Постоянный ток на графике представлен прямой линией и когда он идет по проводу, то электрический заряд, дойдя до обкладки конденсатора упирается в диэлектрик, попадая в тупик. Эта преграда не дает ему пройти.

Синусоидальная же гармоника идет переваливаясь через препятствия и заряд, свободно перекатившись через нарисованные обкладки, теряет небольшую часть энергии, которая зацепилась за пластины.

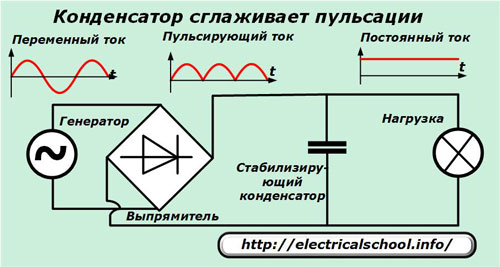
У этой шутки есть скрытый смысл: при подаче на обкладки постоянного или выпрямленного пульсирующего напряжения между пластинами за счет накопления ими электрических зарядов создается строго постоянная разность потенциалов, которая сглаживает все скачки питающей цепи. Это свойство конденсатора увеличенной емкости используется в стабилизаторах постоянного напряжения.

В общем, емкостное сопротивление Xc или противодействие прохождению через него переменному току зависит от конструкции конденсатора, определяющей емкость «С», и выражается формулой:

За счет перезарядки обкладок ток через конденсатор опережает напряжение на 90 градусов.

Реактивное сопротивление линии электропередачи

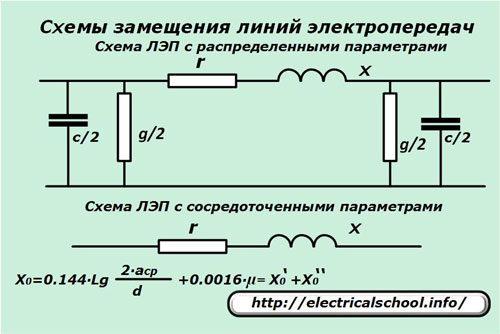
Любая ЛЭП создается для передачи электрической энергии. Ее принято представлять участками со схемами замещения, обладающими распределенными параметрами активного r, реактивного (индуктивного) x сопротивления и проводимости g, отнесенными к единице длины, как правило, одному километру.

Если пренебречь влиянием емкости и проводимости, то можно пользоваться упрощенной схемой замещения линии, обладающей сосредоточенными параметрами.

Передача электроэнергии по неизолированным проводам, расположенным на открытом воздухе, требует значительного удаления их между собой и от земли.

При этом индуктивное сопротивление одного километра провода трехфазной линии можно представить выражением Х0. Оно зависит от:

среднего удаления осей проводов между собой аср;

наружного диаметра фазных жил d;

относительной магнитной проницаемости материала µ;

внешнего индуктивного сопротивления линии Х0’;

внутреннего индуктивного сопротивления линии Х0’’.

Для справки: индуктивное сопротивление 1 км ВЛ, выполненной из цветного металла составляет порядка 0,33÷0,42 Ом/км.

Линия электропередачи, использующая высоковольтный кабель, конструктивно отличается от ВЛ. У нее расстояние между фазами проводов значительно уменьшено и определяется толщиной слоя внутренней изоляции.

Такой трехжильный кабель можно представить в виде конденсатора с тремя обкладками из жил, протянутых на большое расстояние. С увеличением его протяженности возрастает емкость, снижается емкостное сопротивление и увеличивается емкостной ток, замыкающийся по кабелю.

В кабельных линиях под воздействием емкостных токов наиболее часто происходят однофазные замыкания на землю. Для их компенсации в сетях 6÷35 кВ используют дугогасящие реакторы (ДГР), которые подключают через заземленную нейтраль сети. Их параметры подбираются сложными методами теоретических расчетов.

Старые ДГР не всегда эффективно работали из-за низкого качества настройки и несовершенства конструкции. Они создавались под усредненные расчетные токи замыканий, которые часто отличались от реальных значений.

Сейчас внедряются новые разработки ДГР, способные в автоматическом режиме отслеживать аварийные ситуации, быстро замерять их основные параметры и подстраиваться для надежного гашения токов замыкания на землю с точностью до 2%. Благодаря этому эффективность работы ДГР сразу возросла на 50%.

Принцип компенсации реактивной составляющей мощности конденсаторными установками

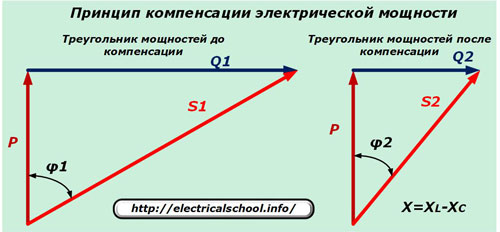
Электрические сети передают высоковольтную электроэнергию на огромные расстояния. Большинством ее потребителей являются электродвигатели, обладающие индуктивным сопротивлением, и резистивные элементы. Полная мощность, направляемая потребителям, состоит из активной составляющей Р, расходуемой на совершение полезной работы, и реактивной Q — вызывающей нагрев обмоток трансформаторов и электродвигателей.

Реактивная составляющая Q, возникая на индуктивных сопротивлениях, снижает качество электроэнергии. Для уничтожения ее вредного воздействия в восьмидесятых годах прошлого века в энергосистеме СССР использовалась схема компенсации за счет подключения конденсаторных батарей, обладающих емкостным сопротивлением, которое снижало косинус угла φ.

Они устанавливались на подстанциях, непосредственно питающих проблемных потребителей. Этим обеспечивалось местное регулирование качества электроэнергии.

Таким способом можно значительно уменьшить нагрузку на оборудование за счет снижения реактивной составляющей при передаче одной и той же активной мощности. Этот способ считается наиболее эффективным приемом энергосбережения не только на промышленных предприятиях, но и на объектах ЖКХ. Его грамотное использование позволяет значительно повысить надежность эксплуатации энергосистем.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Что такое емкостное реактивное сопротивление и как его рассчитать?

Содержание:

В емкостное сопротивление Это сопротивление, которое конденсатор, регулирующий поток заряда в цепи переменного тока, противодействует прохождению тока.

В цепи, состоящей из конденсатора и активируемой источником переменного тока, емкостное реактивное сопротивление X может быть определено_C следующим образом:

Емкостное реактивное сопротивление зависит от обратной частоты, поэтому на высоких частотах оно обычно мало, а на низких частотах реактивное сопротивление велико.

Пока идет заряд, через конденсатор устанавливаются переменное напряжение и ток, амплитуды или максимальные значения которых обозначаются соответственно как V_C и я_C, связаны емкостным сопротивлением аналогично закону Ома:

В конденсаторе напряжение на 90 ° отстает от тока или ток на 90 ° опережает ток, как вы предпочитаете. В любом случае частота такая же.

Когда X_C очень большой, ток имеет тенденцию быть маленьким, и значение X стремится к бесконечности_C, конденсатор ведет себя как разомкнутая цепь и ток равен нулю.

Как рассчитать емкостное реактивное сопротивление

Рассмотрим пример расчета емкостного реактивного сопротивления: предположим, что конденсатор 6 мкФ подключен к розетке переменного тока с напряжением 40 В и частотой F 60 Гц.

Для определения емкостного реактивного сопротивления используется определение, данное в начале. Угловая частота ω определяется как:

Затем этот результат подставляется в определение:

Теперь посмотрим на амплитуду тока, циркулирующего в цепи. Поскольку источник предлагает напряжение амплитудой V_C = 40 В, мы используем соотношение между емкостным реактивным сопротивлением, током и напряжением для вычисления амплитуды тока или максимального тока:

я_C = V_C / ИКС_C = 40 В / 442,1 Ом = 0,09047 А = 90,5 м А.

Если частота становится очень большой, емкостное реактивное сопротивление становится небольшим, но если частота становится равной 0 и у нас есть постоянный ток, реактивное сопротивление стремится к бесконечности.

Ток и напряжение на конденсаторе

Когда конденсатор подключен к источнику переменного тока, когда он колеблется и меняет свою полярность, конденсатор испытывает переменные заряды и разряды.

Для частоты 60 Гц, такой как в примере, напряжение положительное 60 раз в секунду и отрицательное еще 60 раз в секунду.

По мере увеличения напряжения он толкает ток в одном направлении, но если конденсатор разряжается, он производит ток в противоположном направлении, противоположном первому.

C = q / V → q (t) = CV = CV_м сен ωt

И имея нагрузку как функцию времени, у нас будет ток, который является производной от этого:

Но синус и косинус связаны соотношением: cos α = sin (α + π / 2), следовательно:

я_C(t) = CV_м ω sin (ωt + π / 2) = I_C грех (ωt + π / 2)

Как видите, существует разница в 90º опережения тока по отношению к напряжению, как было сказано в начале.

В описании этого типа схем используется понятие фазор, который очень похож на вектор и позволяет представить любую переменную величину, такую ​​как ток, напряжение или импеданс, на комплексной плоскости.

На следующем рисунке справа показаны векторы напряжения и тока в конденсаторе, которые образуют между ними угол 90º, который представляет собой разность фаз между ними.

Слева соответствующие графики, разных амплитуд, но одинаковой частоты. Со временем ток опережает напряжение, и когда он максимален, ток равен нулю, а когда напряжение равно нулю, ток максимален, но с обратной полярностью.

Комплексное сопротивление конденсатора

Фактически, импеданс цепи определяется как отношение напряжения к току:

Для конденсатора или конденсатора его импеданс определяется отношением:

Z_C = v (t) / i (t) = V_C sin ωt / I_C грех (ωt + π / 2)

Импеданс последовательной RC-цепи

Импеданс цепи переменного тока с резисторами, конденсаторами и катушками индуктивности также может быть представлен биномиально следующим образом:

Если в цепи последовательно соединены резистор и конденсатор, их полное сопротивление составляет:

Например, в схеме, показанной ниже, источник имеет вид:

Учитывая, что ω = 120π, импеданс равен:

Приложения с емкостным реактивным сопротивлением

Фильтры верхних частот, фильтры нижних частот, мостовые схемы для измерения емкости и индуктивности и схемы фазового сдвига являются одними из основных применений схем, которые содержат емкостные реактивные сопротивления в сочетании с индуктивностями и электрическими сопротивлениями.

В стереосистемах некоторые динамики поставляются с отдельными динамиками. вуфер (больше) для низких частот и твитер или небольшой рог для высоких частот. Это улучшает производительность и качество звука.

В них используются конденсаторы, которые предотвращают попадание низких частот в высокочастотный динамик, а в низкочастотном динамике добавлен индуктор, чтобы избежать высокочастотных сигналов, поскольку индуктивность имеет реактивное сопротивление, пропорциональное частоте: X_L = 2πfL.

Ссылки

Обычный коммерческий иск: из чего он состоит, этапы и пример

Простые машины: история, характеристики, виды, примеры

Источник

Активное и реактивное сопротивление

В этой статье мы поведем речь о таких параметрах, как активное и реактивное сопротивление.

Активное сопротивление

И начнем мы статью не с реактивного сопротивления, как ни странно, а с простого и всеми нами любимого радиоэлемента — резистора, который, как говорят, обладает активным сопротивлением. Еще иногда его называют омическим. Как нам говорит вики-словарь, «активный — это деятельный, энергичный, проявляющий инициативу». Активист готов всегда рвать и метать даже ночью. Он готов ПОЛНОСТЬЮ выложиться и потратить всю энергию во благо общества.

То же самое можно сказать и про другие нагрузки, обладающие активным сопротивлением. Это могут быть различные нагревательные элементы, типа тэнов, а также лампы накаливания.

Как смотреть силу тока в цепи через осциллограф

Чем же резистор отличается от катушки индуктивности и конденсатора? Понятное дело, что выполняемыми функциями, но этим все не ограничивается. Итак, давайте рассмотрим самую простую схемку во всей электронике:

На схеме мы видим генератор частоты и резистор.

Давайте визуально посмотрим, что у нас творится в этой схеме. Для этого, как я уже сказал, нам понадобится генератор частоты

Но ведь осциллограф предназначен для того, чтобы рассматривать форму сигнала напряжения? Как же мы будем рассматривать форму сигнала силы тока? А все оказывается просто). Для этого достаточно вспомнить правило шунта.

Кто не помнит — напомню. Имеем обыкновенный резистор:

Что будет, если через него прогнать электрический ток?

На концах резистора у нас будет падение напряжения. То есть, если замерить с помощью мультиметра напряжение на его концах, мультиметр покажет какое-то значение в Вольтах

И теперь главный вопрос: от чего зависит падение напряжения на резисторе? В дело опять же вступает закон Ома для участка цепи: I=U/R. Отсюда U=IR. Мы видим зависимость от номинала самого резистора и от силы тока, текущей в данный момент в цепи. Слышите? От СИЛЫ ТОКА! Так почему бы нам не воспользоваться таким замечательным свойством и не глянуть силу тока через падение напряжения на самом резисторе? Ведь номинал резистора у нас постоянный и почти не изменяется с изменением силы тока 😉

Осциллограмма силы тока на активном сопротивлении

В данном опыте нам не обязательно знать номинал силы тока в цепи. Мы будем просто смотреть, от чего зависит сила тока и изменяется ли вообще?

Поэтому, наша схема примет вот такой вид:

В этом случае шунтом будет являться резистор сопротивлением в 0,5 Ом. Почему именно 0,5 Ом? Да потому что он не будет сильно греться, так как обладает маленьким сопротивлением, а также его номинал вполне достаточен, чтобы снять с него напряжение.

Частота 30 Килогерц:

Как вы видите, с ростом частоты сила тока у нас осталась такой же.

Давайте побалуемся формой сигнала:

Как мы видим, сила тока полностью повторяет форму сигнала напряжения.

Итак, какие можно сделать выводы?

1) Сила тока через активное (омическое) сопротивление имеет такую же форму, как и форма напряжения.

2) Сила тока и напряжение на активном сопротивлении совпадают по фазе, то есть куда напряжение, туда и ток. Они двигаются синфазно, то есть одновременно.

3) С ростом частоты ничего не меняется (если только на очень высоких частотах).

Конденсатор в цепи переменного тока

Ну а теперь давайте вместо резистора поставим конденсатор.

Как вы видите, конденсатор обладает сопротивлением, так как сила тока в цепи значительно уменьшилась. Но обратите внимание, что произошел сдвиг желтой осциллограммы, то бишь осциллограммы силы тока.

Вспоминаем алгебру старшие классы. Итак, полный период T — это 2П

Теперь давайте прикинем, какой сдвиг фаз у нас получился на графике:

Где-то примерно П/2 или 90 градусов.

Почему так произошло? Во всем виновато физическое свойство конденсатора. В самые первые доли секунд, конденсатор ведет себя как проводник с очень малым сопротивлением, поэтому сила тока в этот момент будет максимальна. В этом можно легко убедиться, если резко подать на конденсатор напряжение и в начальный момент времени посмотреть, что происходит с силой тока

Красная осциллограмма — это напряжение, которое мы подаем на конденсатор, а желтая — это сила тока в цепи конденсатора. По мере заряда конденсатора сила тока падает и достигает нуля при полном заряде конденсатора.

К чему приведет дальнейшее увеличение частоты? Давайте посмотрим:

Как вы видите, с увеличением частоты, у нас сила тока в цепи с конденсатором возрастает.

Реактивное сопротивление конденсатора

Как мы увидели с прошлого опыта, с увеличением частоты растет сила тока! Кстати, у резистора не росла. То есть получается в данном случае из закона Ома, что сопротивление конденсатора зависит от частоты! Да, все так оно и есть. Но называется оно не просто сопротивлением, а реактивным сопротивлением и вычисляется по формуле:

Х_с — реактивное сопротивление конденсатора, Ом

П — постоянная и приблизительно равна 3,14

С — емкость конденсатора, Фарад

Катушка индуктивности в цепи переменного тока

Ну а теперь давайте возьмем катушку индуктивности вместо конденсатора:

Проводим все аналогичные операции, как и с конденсатором. Смотрим на осциллограммы в цепи с катушкой индуктивности:

Если помните, вот такую осциллограмму мы получили в схеме с конденсатором:

Видите разницу? На катушке индуктивности ток отстает от напряжения на 90 градусов, на П/2, или, как еще говорят, на четверть периода (весь период у нас 2П или 360 градусов).

Так-так-так…. Давайте соберемся с мыслями. То есть в цепи с переменным синусоидальным током, ток на конденсаторе опережает напряжение на 90 градусов, а на катушке индуктивности ток отстает от напряжения тоже на 90 градусов? Да, все верно.

Почему на катушке ток отстает от напряжения?

Не будем углубляться в различные физические процессы и формулы, просто сочтем за данность, что сила тока не может резко возрастать на катушке индуктивности. Для этого проведем простой опыт. Так же как и на конденсатор, мы резко подадим напряжение на катушку индуктивности, и посмотрим, что случилось с силой тока.

Как вы видите, при резкой подаче напряжения на катушку, сила тока не стремится также резко возрастать, а возрастает постепенно, если быть точнее, по экспоненте.

Давайте вспомним, как это было у конденсатора:

Все с точностью наоборот! Можно даже сказать, что катушка — это полная противоположность конденсатору 😉

Ну и напоследок давайте еще побалуемся частотой:

С уменьшением частоты сила тока через катушку увеличивается.

Реактивное сопротивление катушки индуктивности

Из опыта выше мы можем сделать вывод, что сопротивление катушки зависит от частоты и вычисляется по формуле

Х_L — сопротивление катушки, Ом

П — постоянная и равна приблизительно 3,14

Х_L — сопротивление катушки, Ом

П — постоянная и равна приблизительно 3,14

Х_L — сопротивление катушки, Ом

П — постоянная и равна приблизительно 3,14

Х_L — реактивное сопротивление катушки, Ом

П — постоянная и равна приблизительно 3,14

П — постоянная и приблизительно равна 3,14

Мощность в цепи с реактивными радиоэлементами

Для дальнейшего объяснения этого явления нам потребуется наша осциллограмма с катушки индуктивности:

Итак, давайте выделим на ней один период и разделим его на 4 части, то есть по 90 градусов каждая или π/2.

Давайте начнем с такого понятия, как мощность. Если не забыли, мощность — это сила тока помноженное на напряжение, то есть P=IU. Итак, в первую четвертинку периода t1 у нас напряжение принимает положительные значения и сила тока тоже положительное. Плюс на плюс дает плюс. В эту четверть периода энергия поступает из источника в реактивное сопротивление.

Теперь давайте рассмотрим отрезок времени t2. Здесь ток со знаком «плюс», а напряжение со знаком «минус». В итоге плюс на минус дает минус. Получается мощность со знаком «минус». А разве так бывает? Еще как бывает! В этот промежуток времени реактивный радиоэлемент отдает запасенную энергию обратно в источник напряжения. Для лучшего понимания давайте рассмотрим простой житейский пример.

Представим себе кузнеца за работой:

Не знаю, какое было у вас детство, но я когда был пацаном, брал свинец с аккумуляторов и плющил его в металлические пластинки. И что думаете? Свинец нагревался. Не так, чтобы прям обжигал, а был тепленький на ощупь. То есть моя энергия удара превращалась в тепло, можно даже сказать, в полезную энергию.

А что если взять пружину от стоек ВАЗа и ударять по ней?

С пружиной не станет НИ-ЧЕ-ГО! Она ведь не свинец. Но… заметьте вот такую вещь: как только мы начинаем «плющить» пружину кувалдой, у нас она начинает сжиматься. И вот она сжалась до упора и… выстрелила вверх, подхватив с собой тяжелую кувалду, которая только что пыталась ее расплющить. То есть в данном случае энергия вернулась обратно в источник энергии, то есть обратно к кузнецу. Он вроде как и пытался расплющить пружину, но пружина вернула энергию обратно своим разжатием. То есть кузнецу не надо уже было подымать тяжелый молот, так как за него это уже сделала пружина.

Разжатие пружины и возврат ею энергии обратно — это и есть отрицательная мощность. В этом случае энергия возвращается обратно в источник. Хорошо ли это или плохо — это уже другая история.

В третий промежуток времени t3 и ток и напряжение у нас со знаком «минус». Минус на минус — это плюс. То есть реактивный элемент снова поглощает энергию, ну а на t4, снова ее отдает, так как плюс на минус дает минус.

В результате за весь период у нас суммарное потребление энергии равно чему?

Так что же это получается тогда? На катушке и конденсаторе не будет выделяться никакой энергии? Получается так. Поэтому в схемах они чаще всего холодные, хотя могут быть и слегка теплыми, так как реальные параметры катушки и конденсатора выглядят совсем по другому.

Эквивалентная схема реальной катушки индуктивности выглядит вот так:

R_L — это сопротивление потерь. Это могут быть потери в проводах, так как любой провод обладает сопротивлением. Это могут быть потери в диэлектрике, потери в сердечнике и потери на вихревые токи. Как видите, раз есть сопротивление, значит на нем может выделяться мощность, то есть тепло.

L — собственно сама индуктивность катушки

С — межвитковая емкость.

А вот и эквивалентная схема реального конденсатора:

r — сопротивление диэлектрика и корпуса между обкладками

С — собственно сама емкость конденсатора

ESI (ESL) — эквивалентная последовательная индуктивность

Здесь мы тоже видим такие параметры, как r и ESR, которые на высоких частотах будут еще лучше себя проявлять, благодаря скин-эффекту. Ну и, соответственно, на них будет выделяться мощность, что приведет к небольшому малозаметному нагреву.

Резюме

Резистор обладает активным (омическим) сопротивлением. Катушка индуктивности и конденсатор обладают реактивным сопротивлением.

В цепи переменного тока на конденсаторе ток опережает напряжение на 90 градусов, а на катушке ток отстает от напряжения на 90 градусов.

Сопротивление катушки вычисляется по формуле

Сопротивление конденсатора вычисляется по формуле:

В цепи переменного тока на идеальном реактивном сопротивлении не выделяется мощность.

Реальные катушка и конденсатор имеют в своем составе паразитные параметры, которые имеют некоторое сопротивление. Поэтому реальные катушка и конденсатор не обладают чисто реактивным сопротивлением.

Источник