в чем измеряется разность фаз

Фаза колебаний.

Фаза колебаний — это аргумент периодически изменяющейся функции, описывающей колебательный или волновой процесс. Для гармонических колебаний:

где φ = ωt + φ₀ — фаза колебания, А — амплитуда, ω — круговая частота, t — время, φ₀ — началь­ная (фиксированная) фаза колебания; в момент времени t = 0φ = φ₀. Фаза выражается в радианах.

Фаза гармонического колебания при постоянной амплитуде определяет не только координату колеблющегося тела в любой момент времени, но и скорость и ускорение, которые тоже изменяются по гармоническому закону (скорость и ускорение гармонических колебаний — это первая и вторая производные по времени функции (см. рис. ниже), которые, как известно, снова дают синус и косинус). Поэтому можно сказать, что фаза определяет при заданной амплитуде состояние ко­лебательной системы в любой момент времени.

Два колебания с одинаковыми амплитудами и частотами могут отличаться друг от друга фазами. Так как ω = 2π/Т, то

Отношение t/T показывает, какая часть периода прошла от момента начала колебаний. Любому значению времени, выра­женному в долях периода, соответствует значение фазы, выраженной в радианах.

Сплошная кривая на рисунке — это зависимость координаты от времени и одновременно от фа­зы колебаний (верхние и нижние значения на оси абсцисс соответственно) для точки, совершающей гармонические колебания по закону:

Здесь начальная фаза равна нулю φ₀ = 0. В начальный момент времени амплитуда максимальна. Это соответствует случаю колебаний тела, прикрепленного к пружине (или маятника), которое в начальный момент времени отвели от положения равновесия и отпустили. Описание колебаний, начинающихся из положения равновесия (например, при кратковременном толчке покоящегося шарика), удобнее вести с помощью функции синуса:

Как известно, cos φ = sin (φ + π/2), поэтому колебания, описываемые уравнениями x = x_m cos ω₀ t и x = x_m sin ω₀ t, отличаются друг от друга только фазами. Разность фаз, или сдвиг фаз, составляет π/2. Чтобы определить сдвиг фаз, нужно колеблющуюся величину выразить через одну и ту же три­гонометрическую функцию — косинус или синус. Пунктирная кривая на рисунке выше (это график уравнения x = x_m sin ω₀ t) сдвинута относительно сплошной на π/2.

Источник

Характеристики колебаний

Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):

Такие величины, как амплитуду и период, можно определить по графику колебаний.

Начальную фазу, так же, определяют по графику, с помощью интервала времени \(\large \Delta t\), на который относительно нуля сдвигается начало ближайшего периода.

Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.

А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.

Что такое амплитуда

Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.

Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.

В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.

Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.

К примеру, пусть колеблется величина \( \large x \). Тогда символом \( \large x_ <0>\) обозначают амплитуду колебаний этой величины.

Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».

С помощью графика амплитуду можно определить так (рис. 2):

Что такое период

Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.

Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.

\( \large T \left( c \right) \) – период колебаний.

Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.

Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.

Период – это время одного полного колебания.

На графике период найти удобнее одним из таких способов (рис. 4):

Что такое частота

Обозначают ее с помощью греческой буквы «ню» \( \large \nu \).

Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».

Поэтому, размерность частоты — это единицы колебаний в секунду:

\( \large \nu \left( \frac<1> \right) \).

Иногда в учебниках встречается такая запись \( \large \displaystyle \nu \left( c^ <-1>\right) \), потому, что по свойствам степени \( \large \displaystyle \frac<1> = c^ <-1>\).

Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.

Одно колебание в секунду соответствует частоте в 1 Герц.

Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:

Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).

Что такое циклическая частота

Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол \(\large 2\pi\) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный \(\large 2\pi\) секунд.

Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:

\( \large \displaystyle \omega \left( \frac<\text<рад>> \right) \)

Примечание: Величину \( \large \omega \) так же называют круговой частотой, а еще — угловой скоростью (ссылка).

Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за \(\large 2\pi\) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный \(\large 2\pi\) секунд?».

Обычная \( \large \nu \) и циклическая \( \large \omega \) частота колебаний связаны формулой:

Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.

Чтобы с помощью графика колебаний определить величину \( \large \omega \), нужно сначала найти период T.

Затем, воспользоваться формулой \( \large \displaystyle \nu = \frac<1>\) и вычислить частоту \( \large \nu \).

И только после этого, с помощью формулы \( \large \omega = 2\pi \cdot \nu \) посчитать циклическую \( \large \omega \) частоту.

Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.

Определить величину \( \large \omega \) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный \(\large 2\pi\), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).

Что такое начальная фаза и как определить ее по графику колебаний

Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.

Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, \(\large \varphi_ <0>\).

\(\large \varphi_ <0>\left(\text <рад>\right) \) — начальная фаза, измеряется в радианах (или градусах).

Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.

Рассмотрим теперь, как величина \(\large \varphi_ <0>\) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.

Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы \(\large \varphi_ <0>\) принимаем равной нулю.

Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время \(\large \Delta t\), начальный угол \(\large \varphi_ <0>\) будет отличаться от нулевого значения.

Определим угол \(\large \varphi_ <0>\) с помощью графика колебаний.

Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина \(\large \varphi_ <0>\) — в радианах. Значит, нужно связать формулой кусочек времени \(\large \Delta t\) и соответствующий ему начальный угол \(\large \varphi_ <0>\).

Как вычислить начальный угол по интервалу смещения

Алгоритм нахождения начального угла состоит из нескольких несложных шагов.

\[\large T = 5 – 1 = 4 \left( \text <сек>\right)\]

Из графика следует, что период T = 4 сек.

Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.

Для этого используем формулу:

\(\large \displaystyle \frac<1> <4>\cdot 2\pi = \frac<\pi > <2>=\varphi_ <0>\)

Значит, интервалу \(\large \Delta t\) соответствует угол \(\large \displaystyle \frac<\pi > <2>\) – это начальная фаза для красной кривой на рисунке.

Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:

Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол \(\large \displaystyle \frac<\pi > <2>\) имеет знак «плюс».

Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая \(\large \varphi_ <0>= 0 \).

Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».

А если функция сдвинута вправо и запаздывает относительно обычной функции, величину \(\large \varphi_ <0>\) записываем со знаком «-».

Примечания:

Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.

Что такое фаза колебаний

Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.

В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают \(\varphi\).

Различия между фазой и начальной фазой

Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.

Первый угол называют начальной \( \varphi_<0>\) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто \( \varphi\) фазой (рис. 10б) – это величина переменная.

Как на графике колебаний отметить фазу

На графике колебаний фаза \(\large \varphi\) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.

На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.

А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.

Как определить фазу с помощью формулы

Пусть нам известны величины \(\large \omega\) — циклическая частота и \(\large \varphi_<0>\) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.

Время колебаний t будет величиной переменной.

Фазу \(\large \varphi\), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:

Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.

Что такое разность фаз

Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.

Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.

\( \large \varphi_<01>\) – для первого процесса и,

\( \large \varphi_<02>\) – для второго процесса.

Определим разность фаз между первым и вторым колебательными процессами:

Величина \(\large \Delta \varphi \) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.

Как связаны характеристики колебаний — формулы

Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.

Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.

\( \large T \left( c \right) \) – время одного полного колебания (период колебаний);

\( \large N \left( \text <шт>\right) \) – количество полных колебаний;

\( \large t \left( c \right) \) – общее время для нескольких колебаний;

\(\large \nu \left( \text <Гц>\right) \) – частота колебаний.

\(\large \displaystyle \omega \left( \frac<\text<рад>> \right) \) – циклическая (круговая) частота колебаний.

\(\large \varphi_ <0>\left( \text <рад>\right) \) — начальная фаза;

\(\large \varphi \left( \text <рад>\right) \) – фаза (угол) в выбранный момент времени t;

\(\large \Delta t \left( c \right) \) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.

Источник

Общие сведения об измерении разности фаз

Понятие «фаза» характеризует гармоническое (синусоидальное) ко­лебание в любой конкретный момент времени. Для гармонического ко­лебания u₁(t) = U_m1sin(wt +j) с амплитудой U_m1 и круговой частотой w текущая (мгновенная) фаза в момент времени t равна

Фазовым сдвигом Dj двух гармонических сигналов одинаковой час­тоты u₁(t) = U_m1sin(wt +j₁) и u₂(t) = U_m2sin(wt +j₂) называется модуль разности их начальных фаз:

Отметим, что на практике обычно решают задачу измерения разно­сти фаз двух гармонических (синусоидальных) колебаний с равными частотами. Фазовый сдвиг удобнее представить как зависимость сдвига сигналов во времени Dt, соответствующего их идентичным фазам. Так, например, для синусоидальных сигналов u₁(t) = U_m1sinwt и u₂(t) = U_m2sinw(t-Dt), имеющих одинаковый период Т= 2p/w — сдвиг фазы (рис. 12.1, а) равен

Два сигнала называются синфазными, противофазными и находящи­мися в квадратуре, если фазовый сдвиг между ними равен 0, p и p/2 соот­ветственно. Применительно к периодическим синусоидальному и неси­нусоидальному сигналам (рис. 12.1, б) и к двум несинусоидальным сигна­лам с одинаковым периодом Т используется понятие об их сдвиге (задержке) во времени Dt.

Для измерения фазового сдвига используются приборы, называемые фазометрами, а в качестве мер такого сдвига — фазовращатели, т.е. ли­нейные четырехполюсники, у которых выходной сигнал задержан по фазе относительно входного. Существуют регулируемые и нерегулируе­мые фазовращатели.

Методы измерения фазового сдвига

К основным методам измерения фазового сдвига относятся:

— преобразования фазового сдвига в импульсы тока,

— дискретного или цифрового счета,

— с преобра­зованием частоты.

Осциллографический метод

Для измерения фазового сдвига с помощью осциллографа применя­ются следующие методы:

Метод линейной развертки реализуется при наблюдении на экране одновременно двух сигналов (см. рис. 12.1). Для этого можно использо­вать двухлучевой осциллограф, подавая сигналы на входы вертикально­го отклонения лучей (входы Y). Можно также применить однолучевой осциллограф, если на его вход Y подавать исследуемые сигналы поочередно через электронный коммутатор. В том и другом вариантах горизонтальные развертки осциллографов должны быть синхронизиро­ваны одним из сигналов. Измерив временные отрезки Dt и Т, вычисляют фазовый сдвиг сигналов в радианах по формуле (12.2) или в градусах по следующему выражению:

При данном методе погрешность измерения фазового сдвига Dj близка к ±(5. 7)° и вызвана нелинейностью развертки, неточностью замера интерва­лов Dt и Т, а также ошибками определения положения оси времени.

Метод синусоидальной развертки или эллипса

Реализуется с помощью однолучевого осциллографа при подаче одного сигнала на вход Y, а второго — на вход X отклонения луча. При этом генератор развертки осциллографа должен быть выключен.

Пусть на входы X и Y были поданы соответственно сигналы u₁(t) = u₁= U_m1sin(wt) и u₂(t) = u₂ = U_m2sin(wt +j), для которых фазовый сдвиг Dj = j (далее в выражениях для u₁(t) и u₂(t) аргумент t везде опущен). Мгновенные отклонения луча на экране по горизонтали и вертикали равны:

где коэффициенты h_x, h_y — чувствительности осциллографа к отклоне­нию луча по горизонтали и вертикали; а = h_xU_m1, b = h_yU_y2 — амплитуды отклонения луча.

Для определения формы фигуры, вычерчиваемой лучом на экране ос­циллографа, найдем ее аналитическую запись. Для этого достаточно исключить из формул (12.4) и (12.5) переменную t и затем представить от­клонение у в зависимости от величины х:

, (3.19)

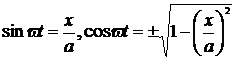
y = b sin(wt +j) = b (sinwt cosj +coswt sinj), (3.20)

После подстановки (12.6) в (12.7) получим выражение

, (3.21)

представляющее собой известное уравнение эллипса (рис. 12.2).

Определим величину фазового сдвига двух сегментов. Частям эл­липса, представленным непрерывной и штриховой линиями (рис. 12.2), соот­ветствует уравнение (12.8), в котором перед корнем стоят знаки плюс и ми­нус соответственно. Величины отрез­ков у₀ и х₀ находятся по уравнению (12.8), если положить для непрерыв­ной линии х = 0, а для штриховой у = 0:

Отсюда искомый фазовый сдвиг:

, (3.22)

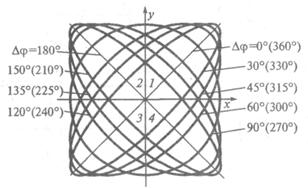
Добиться достаточно точного результата измерений сдвига фаз мож­но, подав один из сигналов на осциллограф через фазовращатель на 90° и проследив за изменением вида осциллограммы. Положим, что имели осциллограмму, соответствующую сдвигу фаз Dj = 60° или 300°. Если теперь подадим сигнал u₂ на вход Y через фазовращатель, то фазовый сдвиг станет равен 150° или 30°. Как видно из рис. 12.3, при Dj = 60° ос­циллограмма из 1-го и 3-го квадрантов переместится в 3-й и 4-й, а при Dj = 300° останется в 1-м и 3-м квадрантах.

Рис. 3.8. Метод эллипса: осциллограммы при разных фазовых сдвигах

Погрешность измерения фазового сдвига между двумя синусоидаль­ными сигналами методом эллипса зависит от точности измерения длин отрезков, входящих в выражение (12.9), и точности фокусировки луча на экране осциллографа. Эти причины оказывают тем большее влияние, чем ближе измеряемый сдвиг фаз к нулю или к 90°. Возможна также сис­тематическая погрешность измерения из-за наличия различного фазово­го сдвига, создаваемого усилителями каналов вертикального и горизон­тального отклонения лучей. Для ее устранения можно (перед началом измерений) подать один из исследуемых сигналов на вход Y осциллографа непосредственно, а на вход X — через регулируемый фазовращатель. Изменяя настройку фазовращателя, необходимо добиться появления на экране осциллографа наклонной прямой линии. Затем, сохраняя эту на­стройку, подать на вход фазовращателя второй сигнал (отключив предвари­тельно первый) и провести требуемое измерение фазового сдвига сигналов.

Метод круговой развертки

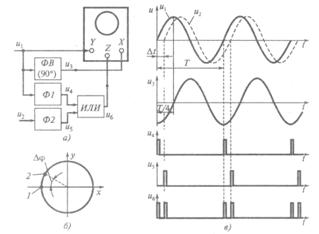
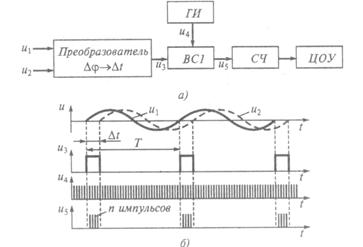
Обеспечивает измерение фазового сдвига практически в пределах от 0 до 360°. Сущность метода поясняется схе­мами и эпюрами, приведенными на рис. 12.4, для случая измерения фазо­вого сдвига между сигналами u₁= U_m1sinwt и u₂ = U_m2sinw(Dt-t).

Рис. 3.9. Метод круговой развертки: а — схема измерения; б — осциллограмма;

Генератор развертки осциллографа предварительно выключается и на входы Y и X подаются сигнал u₁ и сигнал u₃ (рис. 12.4, а), задержанный относительно u₁ по фазе на 90° (с помощью дополнительного фазовращателя ФВ). При одинаковом отклонении электронного луча по гори­зонтали и вертикали на экране осциллографа будет наблюдаться осцил­лограмма, имеющая вид окружности (рис. 12.4, б).

Анализируемые сигналы u₁ и u₂ также поступают на входы идентичных формирователей Ф1 и Ф2, преобразующих синусоидальные колебания в последовательность коротких однополярных импульсов u₄ и u₅ (рис. 12.4, в). Передние фронты этих импульсов практически совпадают с моментом пе­рехода синусоид через нулевое значение при их возрастании. Импульсные сигналы u₄ и u₅ объединяются с помощью логической схемы ИЛИ. Ее выходной импульсный сигнал u₆ в виде двухимпульсных последова­тельностей подается на вход Z управления яркостью луча осциллографа. В результате на окружности (рис. 12.4, б) в точках 1 и 2 появляются от­метки повышенной яркости.

На погрешность измерения влияют точности формирования окруж­ности и определения ее центра, а также степень идентичности порога срабатывания формирователей и точность измерения угла Dj с помо­щью транспортира.

Компенсационный метод

Компенсационный метод основан на сравнении измеряемого фазово­го сдвига с известной величиной фазового сдвига, которую создает изме­рительный фазовращатель.

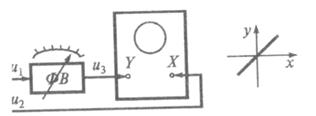
Структурная схема измерительной установки приведена на рис. 12.5. Она содержит измерительный фазовращатель ФВ и индикатор равенства фаз, в качестве которого использован осциллограф с отключенным гене­ратором развертки. Сигнал u₁ подается на вход Y осциллографа через ФВ, а сигнал u₂ на вход X— непосредственно.

Рис. 3.10.К определению фазового сдвига компенсационным методом

Фазовый сдвиг Dj между двумя сигналами u₁ и u₂ определяется путем изменения фазы дополнительного сигнала из с помощью ФВ до момента появления на экране наклонной прямой линии (см. рис. 12.5), т.е. до мо­мента равенства фаз сигналов u₂ и u₃. При этом искомый фазовый сдвиг Dj считывается по шкале ФВ. Для более точных измерений следует проверить и скомпенсировать воз­можное неравенство фазовых сдвигов, даваемых усилителя­ми вертикального и горизон­тального отклонения луча осциллографа. Это выпол­няется в порядке, изложенном выше, при рассмотрении мето­да эллипса.

Суть методов преобразования фазового сдвига в импульсы тока и дискретного или цифрового счета рассмотрим на примере реализации данных методов в средствах измерения разности фаз, которые согласно ГОСТ 15098-86 относятся к подгруппе Ф (Приборы для измерения разности фаз и группового времени запаздывания) и делятся на следующие виды:

Ф1Установки или приборы для поверки измерителей разности фаз и группового времени запаздывания;

Ф2Измерители разности фаз (приборы для измерения разности фаз между двумя сигналами одной частоты);

Ф4Измерители группового времени запаздывания (приборы для измерения крутизны фазочастотных характеристик радиоустройств);

Ф5Измерители разности фаз импульсные (приборы для измерения разности фаз между двумя импульсно-модулированными сигналами одной частоты).

Фазомет­р преобразования фазового сдвига в импульсы тока

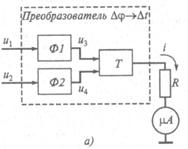
Структурная схема устройства, реализующего метод преобразование фазо­вого сдвига в импульсы тока, и поясняющие его эпюры, приведены на рис. 12.6.

В состав устройства входят преобразователь Dj ®Dt искомого фазового сдвига Dj в интервал времени Dt и измерительный прибор. Преобразователь имеет два одинаковых формирователя Ф1 и Ф2 и триггер Т.

Рис. 3.11. Метод преобразования фазового сдвига в импульсы тока: а — схема устройства; б — эпюры сигналов

Синусоидальные сигналы u₁ и u₂ , имеющие некоторый фазовый сдвиг Dj, подаются на идентичные формирователи Ф1 и Ф2, преобразующие их в последовательности коротких импульсов u₃ и u₄ (рис. 12.6, б). Импульсы u₃ запускают, а импульсы u₄ сбрасывают триггер Т в исходное состояние. В результате на выходе триггера формируется периодическая последова­тельность импульсов напряжения, период повторения и длительность кото­рых равны периоду Т и сдвигу во времени Dt исследуемых сигналов u₁ и u₃. Данные импульсы, поступая на резистор R, соединенный с измерительным прибором mА, преобразуются в последовательность импульсов тока i с ана­логичными периодом и длительностью и некоторой амплитудой I_m (рис. 12.6, б).

В качестве измерительного прибора часто используется микро­амперметр магнитоэлектрической системы, реагирующий на среднее значение тока i за период его следования Т. Пусть S_I и i_cp, — чувстви­тельность прибора и среднее значение протекающего через него тока. Тогда показание прибора а определится по несложной формуле

. (3.23)

С учетом выражения (12.3) получим

, (3.24)

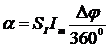
где Dj — искомый фазовый сдвиг.

Так как чувствительность S_I, и ампли­туда I_m постоянны, то шкалу микроамперметра можно проградуировать непосредственно в градусах. Измеренное значение фазового сдвига явля­ется средним за время измерения.

Рассмотренное устройство является прямопоказывающим фазомет­ром с равномерной шкалой. Диапазон его рабочих частот ограничен снизу инерционностью магнитоэлектрического прибора, а сверху — неидеальностью фронтов импульсов формирователей Ф1 и Ф2, влияю­щих на четкость работы триггера Т.

Цифровой фазометр

Метод дискретного счета (более точное название — цифровой метод измерения фазового сдвига), используемый в цифровых фазомет­рах, включает две основные операции:

— преобразование фазового сдвига в соответствующий интервал вре­мени;

— измерение интервала времени методом дискретного счета.

Рассмотрим реализацию метода дискретного счета в простейшем цифровом фазометре (рис. 12.7, а), в состав которого входят преоб­разователь Dj ®Dt искомого фазового сдвигаDj в интервал времени Dt , временной селектор ВС1, генератор счетных импульсов ГИ, счетчик СЧ и цифровое отсчетное устройство ЦОУ.

Рис. 3.12 Цифровой метод измерения фазового сдвига.

а — структурная схема; б — временные диаграммы

Устройство и принцип действия преобразователя Dj ®Dt рассмот­рены выше. Временной селектор представляет собой ключевую логическую схему. Генератор счетных импульсов состоит из кварцевого генератора гармонических колебаний стабильной частоты и схемы фор­мирования импульсов.

Цифровой фазометр работает следующим образом. Преобразователь Dj ®Dt из подаваемых на его входы синусоидальных сигналов u₁ и u₂, имеющих фазовый сдвиг Dj, формирует последовательность прямо­угольных импульсов u₃ (рис. 12.7, б), имеющих длительность Dt и период повторения Т, равные соответственно сдвигу во времени и периоду сиг­налов u₁ и u₂.

Импульсы u₃, а также счетные импульсы u₄ вырабатываемые генера­тором ГИ, подаются на входы временного селектора ВС1. Данный се­лектор открывается на время, равное длительности Dt импульсов u₃, и в течение этого времени пропускает на выход импульсы генератора u₄. При этом на выходе селектора ВС1 формируются пакеты импульсов u₅, следующие с периодом Т.

За один период повторения Т сигналов u₁ и u₂ на счетчик СЧ с выхода селектора поступает количество импульсов, содержащееся в одном паке­те и равное

где T₀ — период следования счетных импульсов генератора ГИ.

Подставляя в (12.12) соотношение для Dt, из (12.3) находим выражение для измеряемого фазового сдвига сигналов u₁ и u₂:

Кодовый сигнал со счетчика, пропорциональный фазовому сдвигу Dj, подается на цифровое отсчетное устройство, показания которого выдаются в градусах.

Погрешность данного цифрового фазометра определяется погрешностью дискретности и аппаратурной погрешностью. Погрешность дискретности связана с тем, что интервал времени Dt можно измерить с точностью до одного периода счетных импульсов. Аппаратурная по­грешность определяется нестабильностью времени срабатывания триг­гера преобразователя Dj ®Dt .

Для уменьшения погрешностей используют фазометры сред­него значения, результат измерения которых является средним значением измеряемого фазового сдвига за большое число периодов Т.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Источник