в чем измеряется радиус окружности

Как найти радиус окружности

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Источник

Радиус и диаметр окружности

Окружность — это фигура в геометрии, которая состоит
из множества точек, расположенных на одинаковом
расстоянии от заданной точки (центра окружности).

Радиус окружности — это отрезок, который соединяет
центр окружности с какой-либо точкой окружности.

Диаметр окружности — это отрезок, который соединяет
две любые точки окружности, причем сам отрезок
должен проходить через центр окружности

Eсли от центра окружности провести
отрезки ко всем точкам окружности, то они будут иметь
одинаковую длину, то есть равны. В математике
такие отрезки называют радиусами.

Все радиусы окружности, как и диаметры окружности,
равны между собой, имеют одинаковую длину.

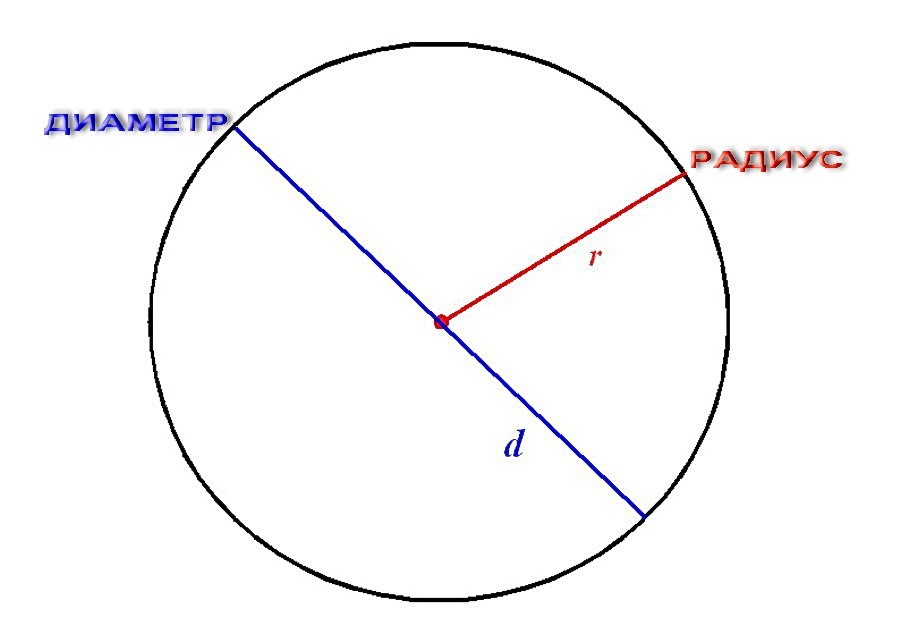
На рисунке выше изображена окружность, с центром в точке O.
OA = OB = OC — радиусы окружности;
BC = CO + OB — диаметр окружности;

Радиус окружности принято обозначать маленькой либо большой буквой, r или R.
Диаметр окружности обозначают буквой D.

Диаметр окружности условно состоит из двух
радиусов и равен длинам этих радиусов.

Длину радиуса окружности можно найти через диаметр окружности.
Для этого достаточно разделить на два длину диаметра окружности,
получившееся число и будет радиусом.

Формула радиуса окружности через диаметр:

Формула диаметра окружности через радиус:

Также, окружность, может быть вписанной в фигуру, описанной
около фигуры; или вообще может быть не вписана и не описана.
Формула радиуса окружности зависит от того находится фигура
внутри окружности, или окружность находится около фигуры.

Существует радиус вписанной окружности
и радиус описанной окружности.

Формулы радиуса вписанной и радиуса описанной окружностей
зависят в первую очередь от геометрической фигуры.

Радиус вписанной окружности — это радиус окружности,
которая вписана в геометрическую фигуру.

Радиус описанной окружности — это радиус окружности,
которая описана около геометрической фигуры.

Источник

Радиус

Ра́диус (лат. radius — спица колеса, луч) — отрезок, соединяющий центр окружности (или сферы) с любой точкой, лежащей на окружности (или поверхности сферы), а также длина этого отрезка. Радиус составляет половину диаметра.

Содержание

Свойства

Связанные определения

Этимология

Обобщения

Радиусом множества , лежащего в метрическом пространстве с метрикой , называется величина . Например, радиус n-размерного гиперкуба со стороной s равен

См. также

Полезное

Смотреть что такое «Радиус» в других словарях:

Радиус-FM — Страна Беларусь … Википедия

РАДИУС — (лат. radius луч). 1) полупоперечник круга; в кривых линиях и кривых поверхностях линия, проведенная от центра в окружности. 2) кость, лежащая рядом с локтевою и образующая с нею локтевую часть руки. Радиус вектор. Расстояние какой нибудь точки… … Словарь иностранных слов русского языка

РАДИУС — муж., лат. полупоперечник круга, полуось шара, луч, нога, которою круг очерчен; черта или мера от остья (средоточия, центра) до обода. Радиус вектор, полупоперечник долгокруга (эллипса). | Радиус, лучевая кость; она лежит рядом с локтевою и с нею … Толковый словарь Даля

РАДИУС — РАДИУС, радиуса, муж. (лат. radius луч, спица). 1. Прямая, соединяющая точку центра с любой точкой окружности или поверхности шара (мат.). 2. перен. Величина охвата чего нибудь, сфера распространения чего нибудь (по отношению к какому нибудь… … Толковый словарь Ушакова

радиус — закругленной части режущей кромки инструмента. [http://www.manual steel.ru/eng a.html] Тематики металлургия в целом EN nose radius … Справочник технического переводчика

РАДИУС — (лат. radius букв. спица колеса, луч), отрезок, соединяющий какую либо точку окружности или сферы с центром, а также длина этого отрезка … Большой Энциклопедический словарь

РАДИУС — РАДИУС, в геометрии расстояние или прямая от центра окружности или сферы к любой точке ОКРУЖНОСТИ или поверхности сферы … Научно-технический энциклопедический словарь

РАДИУС — РАДИУС, а, муж. 1. В математике: отрезок прямой, соединяющий центр шара или круга с любой точкой сферы или окружности, а также длина этого отрезка. 2. перен. Охват, область распространения чего н. Р. действия авиации. | прил. радиусный, ая, ое… … Толковый словарь Ожегова

РАДИУС — (стар.) градшток (см.). Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза ССР, 1941 … Морской словарь

радиус — сущ., кол во синонимов: 2 • критрадиус (1) • отрезок (12) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

Источник

Геометрия. Урок 5. Окружность

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Определение окружности

Окружность – геометрическое место точек, равноудаленных от данной точки.

Отрезки в окружности

Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.

Хорда a – отрезок, соединяющий две точки на окружности.

Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).

O A – радиус, D E – хорда, B C – диаметр.

Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.

Касательная к окружности – прямая, имеющая с окружностью одну общую точку.

Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.

Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).

Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.

Дуга в окружности

Теорема 4:
Равные хорды стягивают равные дуги.

Углы в окружности

В окружности существует два типа углов: центральные и вписанные.

Центральный угол – угол, вершина которого лежит в центре окружности.

∠ A O B – центральный.

Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.

Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.

∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2

∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °

Длина окружности, длина дуги

Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.

Длина окружности находится по формуле:

Площадь круга и его частей

Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.

Круг – часть пространства, которая находится внутри окружности.

Иными словами, окружность – это граница, а круг – это то, что внутри.

Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.

Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.

Площадь круга находится по формуле: S = π R 2

Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Примеры сектора в реальной жизни: кусок пиццы, веер.

Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α

Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.

Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.

Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.

S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α

Теорема синусов

Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с окружностями.

Источник

Диаметр и радиус — что это такое?

В жизни человек часто сталкивается с понятием окружность. Все едят с круглых тарелок, грызут круглые яблоки, катаются на велосипеде или ездят на транспорте с круглыми колесами и просто видят круглое солнце.

Понятия радиус и диаметр

Немногие задумываются, что на самом деле круг – очень сложная замкнутая фигура. Она состоит из главной точки (так называемый центр), а также из множества точек, которые идут от этого центра. Расстояние от центральной точки до окружности называют радиус. Чаще всего это понятие обозначается букой «R».

Если соединить две противоположные друг другу точки окружности и провести между ними линию, то она и будет диаметром. Диаметр обозначают символом «Ø». То есть радиус всегда будет равен половине диаметра.

Как использовать эти понятия в жизни

Вообще с этими понятиями знакомы практически все, кто учил геометрию в школе. Взрослые тоже часто сталкиваются с ними, когда помогают детям делать домашнее задание или просто проверяют его.

Также эти понятия очень часто используются в черчении, к примеру, в архитектуре, когда планируется сделать круглое окно, арку или другую круглую деталь.

В ландшафте тоже не обойтись без радиуса и диаметра, ведь именно они позволят поделить круг на несколько частей, создав яркие цветочные композиции. Последние будут не только радовать глаза, но и помогут отвлечь внимание гостей от грядок с овощами.

Во время конструирования одежды тоже часто встречаются понятия радиус и диаметр. Например, когда шьют шляпы, юбки или круглые накладные воротники.

Понятия диметр и радиус часто используются в программировании и создании сайтов. К примеру, многие создают программы для коррекции кругов (последние используются в разных сферах).

Важно обратить внимание, что понятия диаметр и радиус касаются не только круга. Круг – это фигура, которая лежит на определенной плоскости. Но в геометрии фигуры не всегда лежат на плоскости, некоторые находятся в пространстве. И понятия круг в пространстве вообще не существует, в нем используются объемные фигуры, например, эллипс, цилиндр, конус или шар. Для вычисления объема всех этих фигур тоже понадобится определять диаметр и радиус.

Другие понятия

Существует еще несколько понятий, которые могут пригодиться тем, кто работает с диаметром или радиусом:

Все перечисленные выше понятия пригодятся не только тем, кто учит геометрию, но и тем, кто имеет дело с кругами в других сферах. В математике существует несколько формул, которые помогут выяснить величину любого из описанных выше понятий по заданным параметрам.

Источник