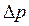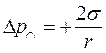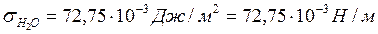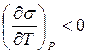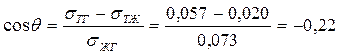в чем измеряется поверхность натяжения
Поверхностное натяжение
Понятие и характеристики поверхностного натяжения
С явлением поверхностного натяжения жидкости мы сталкиваемся каждый день:
Силы поверхностного натяжения действуют вдоль поверхности жидкости, стремясь сократить ее площадь. Как будто жидкость заключена в упругую пленку, которая стремится сжать свое содержимое.
Потенциальная энергия взаимного притяжения молекул жидкости больше их кинетической энергии. Это позволяет веществу сохранять объем (но не форму), и этот объем ограничивается поверхностью жидкости.
На молекулу жидкости, которая находится внутри, действуют силы притяжения со стороны других молекул, и они уравновешивают друг друга. А на ту молекулу, что находится на поверхности, действуют силы притяжения не только со стороны других молекул жидкости, но и со стороны газа (внешней среды). Эти вторые значительно меньше первых, поэтому равнодействующая сила притяжения направлена внутрь жидкости, что способствует удержанию молекулы на поверхности.
Поверхностное натяжение — это стремление жидкости сократить свою свободную поверхность, то есть уменьшить избыток своей потенциальной энергии на границе раздела с газообразной фазой.
Чем больше площадь поверхности жидкости, тем больше молекул, которые обладают избыточной потенциальной энергией, и тем больше поверхностная энергия. Этот факт можно записать в виде следующего соотношения:
Поверхностная энергия жидкости
W = σS
W — поверхностная энергия жидкости [Дж]
S — площадь свободной поверхности [м 2 ]
σ — коэффициент поверхностного натяжения [Н/м]
Отсюда мы можем вывести формулу коэффициента поверхностного натяжения.
Коэффициент поверхностного натяжения — это физическая величина, которая характеризует данную жидкость и численно равна отношению поверхностной энергии к площади свободной поверхности жидкости.
Коэффициент поверхностного натяжения
σ = W/S
W — поверхностная энергия жидкости [Дж]
S — площадь свободной поверхности [м 2 ]
σ — коэффициент поверхностного натяжения [Н/м]
Коэффициент поверхностного натяжения жидкости зависит:
Коэффициент поверхностного натяжения не зависит от площади свободной поверхности жидкости, хотя может быть рассчитан с ее помощью.
Если на жидкость не действуют другие силы или их действие мало, жидкость будет стремиться принимать форму сферы, как капля воды или мыльный пузырь. Так же ведет себя вода в невесомости. Жидкость ведет себя так, как будто по касательной к ее поверхности действуют силы, стягивающие эту поверхность. Эти силы называются силами поверхностного натяжения.
Сила поверхностного натяжения
F = σl
F — сила поверхностного натяжения [Н]
l — длина контура, ограничивающего поверхность жидкости [м]
σ — коэффициент поверхностного натяжения [Н/м]
В химической промышленности в воду часто добавляют специальные реагенты-смачиватели, не дающие ей собираться в капли на какой-либо поверхности. Например, их добавляют в жидкие средства для посудомоечных машин. Попадая в поверхностный слой воды, молекулы таких реагентов заметно ослабляют силы поверхностного натяжения, вода не собирается в капли и не оставляет на поверхности пятен после высыхания.
Поверхностное натяжение
 Механика сплошных сред Механика сплошных сред | ||||||||||
 | ||||||||||
| Сплошная среда | ||||||||||
| ||||||||||
| См. также: Портал:Физика |
Пове́рхностное натяже́ние — термодинамическая характеристика поверхности раздела двух находящихся в равновесии фаз, определяемая работой обратимого изотермокинетического образования единицы площади этой поверхности раздела при условии, что температура, объём системы и химические потенциалы всех компонентов в обеих фазах остаются постоянными.
Сила поверхностного натяжения направлена по касательной к поверхности жидкости, перпендикулярно к участку контура, на который она действует и пропорциональна длине этого участка. Коэффициент пропорциональности 
В 1985 году аналогичный взгляд на физическую природу поверхностного натяжения, как части внутренней энергии, при решении другой физической задачи был опубликован В. Вайскопфом (Victor Frederick Weisskopf) в США (V.F.Weisskopf, American Journal of Physics 53 (1985) 19-20.; V.F.Weisskopf, American Journal of Physics 53 (1985) 618—619.).
Поверхностное натяжение может быть на границе газообразных, жидких и твёрдых тел. Обычно имеется в виду поверхностное натяжение жидких тел на границе «жидкость — газ». В случае жидкой поверхности раздела поверхностное натяжение правомерно также рассматривать как силу, действующую на единицу длины контура поверхности и стремящуюся сократить поверхность до минимума при заданных объёмах фаз.
В общем случае прибор для измерения поверхностного натяжения называется тензиометр.
Содержание
Проявления
Так как появление поверхности жидкости требует совершения работы, каждая среда «стремится» уменьшить площадь своей поверхности:
Математическая теория
Площадь поверхности
С поверхностью жидкости связана свободная энергия
Формула Лапласа
Рассмотрим тонкую жидкую плёнку, толщиной которой можно пренебречь. Стремясь минимизировать свою свободную энергию, плёнка создаёт разность давления с разных сторон. Этим объясняется существование мыльных пузырей: плёнка сжимается до тех пор, пока давление внутри пузыря не будет превышать атмосферное на величину добавочного давления плёнки. Добавочное давление в точке поверхности зависит от средней кривизны в этой точке и даётся формулой Лапласа:
Здесь 

Для случая поверхности кругового цилиндра радиуса 

Обратите внимание, что 
Из формулы Лапласа следует, что свободная мыльная плёнка, натянутая на рамку произвольной формы и не образующая пузырей, будет иметь среднюю кривизну, равную 0.
Зависимость от температуры
С увеличением температуры величина поверхностного натяжения уменьшается и равна нулю при критической температуре. Наиболее известная эмпирическая зависимость поверхностного натяжения от температуры была предложена Лорандом Этвёшом, так называемое правило Этвёша (англ.). В настоящее время получен вывод теоретической зависимости поверхностного натяжения от температуры в области до критических температур, подтверждающей правило Этвёша (журнал «Вестник Санкт-Петербургского университета», 2012, вып. 1, с. 24-28).
Способы определения
Методы
Полностью стандартизованные методы измерений описываются в соответствующих ASTM, ГОСТ и т. д.
Метод вращающейся капли
Сущностью метода является измерение диаметра капли жидкости, вращающейся в более тяжелой жидкости. Этот способ измерения годится для измерения низких или сверхнизких значений межфазного натяжения. Он широко применяется для микроэмульсий, измерения эффективности ПАВ в нефтедобыче, а также для определения адсорбционных свойств.
Метод Дю Нуи (метод отрыва кольца)
Метод является классическим. Сущность метода вытекает из названия. Платиновое кольцо поднимают из жидкости, смачивающей его, усилие отрыва и есть сила поверхностного натяжения и может быть пересчитано в поверхностную энергию. Метод подходит для измерения ПАВ, трансформаторных масел и т. д.
Метод бегущих волн
При возмущении жидкости пластиной «лежащей» на её поверхности, по ней начинает распространяться круг волн. Если просветить кювету с жидкостью импульсным источником света с частотой равной частоте возмущения, то на экран спроецируется «стоячая» волновая картина. Измеряя длину волны на экране и геометрически перерассчитывая её (зная расстояние от источника света до поверхности жидкости и расстояние от поверхности до экрана, а также про подобие треугольников) можно получить величину поверхностного натяжения по формуле:
Единицы измерения поверхностного натяжения
Одна размерность легко выводится из другой:
СИ: Дж/м 2 = Н∙м/м 2 =Н/м;
Влияние различных факторов на величину
Поверхностного натяжения
Влияние химической природы вещества
Поверхностное натяжение – работа, затрачиваемая на разрыв межмолекулярных связей. Поэтому, чем сильнее межмолекулярные связи в данном теле, тем больше его поверхностное натяжение на границе с газовой фазой. Следовательно, поверхностное натяжение меньше у неполярных жидкостей, имеющих слабые межмолекулярные связи, и больше у полярных жидкостей. Большим поверхностным натяжением обладают вещества, имеющие межмолекулярные водородные связи, например вода.
Значения поверхностного натяжения и удельной поверхностной энергии некоторых веществ на границе с воздухом
| Вещество | Т, К | σ·10 3 Дж/м 2 | Вещество | Т, К | σ·10 3 Дж/м 2 |
| Гелий (ж) | 0,22 | Серебро (ж) | |||
| Бензол | 28,2 | * Серебро (т) | |||
| Муравьиная к-та | 36,3 | * Железо (т) | |||
| Вода | 71,96 | * Вольфрам (т) | |||
| Ртуть | 473,5 | * Алмаз |
* – приведены значения удельной поверхностной энергии
Влияние температуры
С ростом температуры расстояние между молекулами увеличивается, с увеличением температуры поверхностное натяжение индивидуальных жидкостей уменьшается, то есть выполняется соотношение:
Для многих жидкостей зависимость σ=f(T) близка к линейной. Экстраполяция линейной зависимости к оси абсцисс определяет критическую температуру ТС данного вещества. При этой температуре двухфазная система жидкость – пар перестает существовать и становится однофазной.
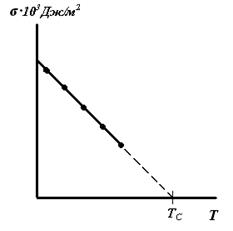 Рис.9.2.Влияние температуры на величину поверхностного натяжения Рис.9.2.Влияние температуры на величину поверхностного натяжения | Для большинства неполярных жидкостей зависимость поверхностного натяжения от температуры выражается уравнением: 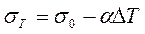 , (9.5) где σТ – поверхностное натяжение при любой температуре, σ0 – поверхностное натяжение при стандартной температуре, ΔТ – разность между данной и стандартной температурой, α – температурный коэффициент поверхностного натяжения: , (9.5) где σТ – поверхностное натяжение при любой температуре, σ0 – поверхностное натяжение при стандартной температуре, ΔТ – разность между данной и стандартной температурой, α – температурный коэффициент поверхностного натяжения: 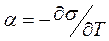 (9.6) (9.6) |
Для многих веществ температурные коэффициенты поверхностного натяжения составляют примерно от –0,1 до –0,2 мДж/(м 2 К).
Влияние природы граничащих фаз
Поверхностное натяжение (σ12) на границе двух жидкостей 1 и 2 зависит от их химической природы (полярности). Чем больше разность полярностей жидкостей, тем больше поверхностное натяжение на границе их раздела (правило Ребиндера).
Количественно межфазное поверхностное натяжение на границе двух взаимно насыщенных жидкостей можно рассчитать по приближенному правилу Антонова.
Правило Антонова (1907):Если жидкости ограниченно растворимы друг в друге, то поверхностное натяжение на границе ж1/ж2 равно разности между поверхностными натяжениями взаимно насыщенных жидкостей на границе их с воздухом или с их собственным паром:
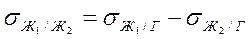
Смачивание
Смачивание – взаимодействие жидкости с твердым или другим жидким телом при наличии одновременного контакта трех несмешивающихся фаз, одна из которых обычно является газом (воздух).
При нанесении небольшого количества жидкости на поверхность твердого тела или на поверхность другой жидкости, имеющей большую плотность, возможно два случая: в первом случае жидкость приобретает форму капли, в другом случае растекается. Рассмотрим первый процесс, когда капля не растекается по поверхности другого тела.
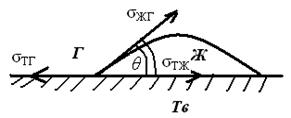 Рис.9.3.Смачвание на границе раздела трех фаз Рис.9.3.Смачвание на границе раздела трех фаз | Рассмотрим каплю жидкости на поверхности твердого тела в условиях равновесия. Так как поверхностное натяжение можно рассматривать как энергию, приходящуюся на единицу площади, или как силу, действующую на единицу длины, то все рассмотренные составляющие поверхностной энергии можно выразить с помощью векторов сил. |
На единицу длины периметра действуют три силы:
1. Поверхностная энергия твердого тела, стремясь уменьшиться, растягивает каплю по поверхности. Эта энергия равна поверхностному натяжению твердого тела на границе с воздухом σТГ.
2. Поверхностная энергия на границе твердого тела с жидкостью σТЖ стремится сжать каплю, то есть поверхностная энергия уменьшается за счет снижения площади поверхности.
3. Поверхностная энергия на границе капли жидкости с воздухом σЖГ направлена по касательной к сферической поверхности капли.
Угол θ, образованный касательными к межфазным поверхностям, ограничивающим смачиваемую жидкость, и имеющий вершину на линии раздела трех фаз, называется краевым углом или углом смачивания.
Проекция вектора σЖГ на горизонтальную ось – произведение σЖГ ·cos θ.
В условиях равновесия:
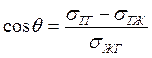
Полученное соотношение (9.9) называют уравнением Юнга.
В зависимости от значений равновесного краевого угла, различают три основных вида смачивания:
Анализ уравнения Юнга
1. Если σТГ> σТЖ, то cos θ > 0 и θ 90° (краевой угол смачивания тупой) – несмачивание. Пример: вода на парафине или тефлоне.
3. Если σТГ = σТЖ, то cos θ = 0 и θ = 90° – граница между смачиваемостью и несмачиваемостью.
4. Если 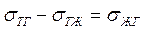
Полного несмачивания, то есть такого положения, когда θ = 180°, не наблюдается, так как при соприкосновении конденсированных тел поверхностная энергия всегда уменьшается.
Различные жидкости неодинаково смачивают одну и ту же поверхность. Согласно приближенному правилу – лучше смачивает поверхность та жидкость, которая ближе по полярности к смачиваемому веществу.
По виду избирательного смачивания все твердые тела делят на три группы:
· Гидрофильные (олеофобные) материалы – лучше смачиваются водой, чем неполярными углеводородами: кварц, силикаты, карбонаты, оксиды и гидроксиды металлов, минералы (краевой угол меньше 90° со стороны воды).
· Гидрофобные (олеофильные) материалы –лучше смачиваются неполярными жидкостями, чем водой: графит, уголь, сера, парафин, тефлон.
Решение:
По закону Юнга:
cos θ 90° – данная поверхность водой не смачивается.
Флотация
Флотация относится к наиболее распространенным методам обогащения полезных ископаемых. Этим методом обогащается около 90% руд цветных металлов, уголь, сера и другие природные материалы.
Флотационное обогащение (разделение) основано на различной смачиваемости водой ценных минералов и пустой породы. В случае пенной флотации через водную суспензию измельченной руды (пульпу) барботируют воздух, к пузырькам которого прилипают гидрофобные частицы ценного минерала (чистые металлы или их сульфиды), всплывающие затем на поверхность воды, и с образовавшейся пеной снимаются механически для дальнейшей переработки. Пустая порода (кварц, алюмосиликаты) хорошо смачивается водой и оседает во флотационных машинах.
Пример 9.2. Порошок кварца и серы высыпали на поверхность воды. Какое явление можно ожидать, если краевой угол смачивания для кварца 0°, а для серы 78°.
Решение:
Так как для кварца θ = 0° – полное смачивание, то кварц будет полностью смачиваться водой и оседать на дно емкости. Краевой угол смачивания для серы близок к 90°, следовательно, порошок серы будет образовывать суспензию на поверхности воды.
Особенности искривленной поверхности раздела фаз
Рассмотрим еще одно важное качество дисперсных систем, связанное с раздробленностью – резкое увеличение кривизны поверхности частиц по сравнению с плоскостью.
За счет кривизны поверхности жидкой дисперсной фазы возникает избыточное внутримолекулярное давление 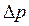
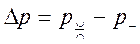
где 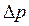
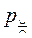
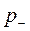
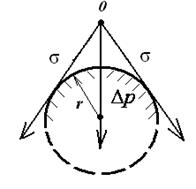 Рис. 9.5. Схема образования избыточного внутреннего давления Рис. 9.5. Схема образования избыточного внутреннего давления 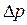 с положительной кривизной. с положительной кривизной. | Равнодействующая сил поверхностного натяжения 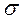 как векторная величина компенсируется силой как векторная величина компенсируется силой 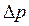 , которая направлена к центру частицы и перпендикулярна ее поверхности. В результате искривления поверхности совершается работа , которая направлена к центру частицы и перпендикулярна ее поверхности. В результате искривления поверхности совершается работа 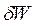 , которая приводит к уменьшению объема тела на величину dV. , которая приводит к уменьшению объема тела на величину dV. 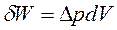 . (9.11) . (9.11) |
Уравнение, связывающее избыточное внутримолекулярное давление 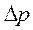
· для сферической поверхности:
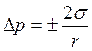
· для цилиндрической поверхности:
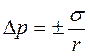
· для частиц произвольной формы:
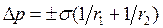
Уравнения (9.12-9.14) представляет собой закон капиллярного давления Лапласа для сферической, цилиндрической поверхностей и поверхности произвольной формы.
Кривизна поверхности может быть положительной и отрицательной. Если центр окружности находится внутри тела (рис.9.5), то кривизна поверхности считается положительной, тогда