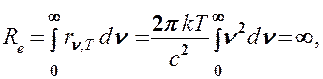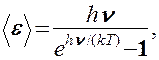в чем измеряется постоянная вина

Закон смещения Вина

Зако́н смеще́ния Ви́на даёт зависимость длины волны, на которой поток излучения энергии чёрного тела достигает своего максимума, от температуры чёрного тела.

Содержание

Общий вид закона смещения Вина

Для частоты света (в герцах) закон смещения Вина имеет вид:

Вывод закона

Для вывода можно использовать выражение закона излучения Планка для абсолютно чёрного тела, записанного для длин волн:

Чтобы найти экстремумы этой функции в зависимости от длины волны, её следует продифференцировать по и приравнять дифференциал к нулю:

Из этой формулы сразу можно определить, что производная приближается к нулю, когда или когда , что выполняется при . Однако, оба эти случая дают минимум функции Планка , которая для указанных длин волн достигает своего нуля (см. рисунок вверху). Поэтому анализ следует продолжить лишь с третьим возможным случаем, когда

Используя замену переменных , данное уравнение можно преобразовать к виду

Численное решение этого уравнения даёт: [1]

Таким образом, используя замену переменных и значения постоянных Планка, Больцмана и скорости света, можно определить длину волны, на которой интенсивность излучения абсолютно чёрного тела достигает своего максимума, как

где температура дана в кельвинах, а — в метрах.

Примеры

Согласно закону смещения Вина человеческое тело с температурой 290 K (+17°C) имеет максимум теплового излучения на длине волны 10 μм, что соответствует инфракрасному диапазону спектра.

Реликтовое излучение имеет эффективную температуру 2,7 K и достигает своего максимума на длине волны 1 мм. Соответственно эта длина волны принадлежит уже радиодиапазону.

История

Вильгельм Вин впервые вывел этот закон в 1893 году путём применения законов термодинамики к электромагнитному излучению.

См. также

Ссылки

Источники и примечания

Полезное

Смотреть что такое «Закон смещения Вина» в других словарях:

закон смещения Вина — Vyno poslinkio dėsnis statusas T sritis fizika atitikmenys: angl. Wien’s displacement law vok. Wiensches Verschiebungssatz, m rus. закон смещения Вина, m pranc. loi de déplacement de Wien, f … Fizikos terminų žodynas

закон смещения Вина — [Wien s displacement law] длина волны (λмах), на которую приходится максимум энергии в спектре равновесного излучения, обратно пропорционально абсолютной температуре, излучающего тела: λмах • Т = b, где b постоянная Вина. Впервые получен немецким … Энциклопедический словарь по металлургии

закон излучения Вина — [Wien s radiation law] распределения энергии в спектре равновесного излучения в зависимости от абсолютной температуры (T). Открыт немецким физиком В. Вином, который в 1883 г. вывел формулу для общего вида распределения энергии в спектре… … Энциклопедический словарь по металлургии

ВИНА ЗАКОН СМЕЩЕНИЯ — закон, утверждающий, что длина волны l,макс, на к рую приходится максимум энергии в спектре равновесного излучения, обратно пропорциональна абс. темп ре T излучающего тела: lмаксT=b (b постоянная Вина). В. з. с. является следствием формулы Вина… … Физическая энциклопедия

ВИНА ЗАКОН СМЕЩЕНИЯ — ВИНА ЗАКОН СМЕЩЕНИЯ: длина волны на которую приходится максимум энергии в спектре равновесного излучения, обратно пропорциональна абсолютной температуре излучающего тела. Выведен в 1893 В. Вином … Большой Энциклопедический словарь

ВИНА ЗАКОН СМЕЩЕНИЯ — ВИНА ЗАКОН СМЕЩЕНИЯ: длина волны, на которую приходится максимум энергии в спектре равновесного излучения, обратно пропорциональна абсолютной температуре излучающего тела. Выведен в 1893 В. Вином … Энциклопедический словарь

Вина закон смещения — закон, утверждающий, что длина волны λмакс, на которую приходится максимум энергии в спектре равновесного излучения, обратно пропорциональна абсолютной температуре Т излучающего тела: λмакс·Т = b, где b постоянная, равная 0,2897 см·К. В.… … Большая советская энциклопедия

ВИНА ЗАКОН СМЕЩЕНИЯ — [по имени нем. физика В. Вина (W. Wien; 1864 1928)] закон теплового излучения, согласно к рому длина волны Лmах, соответствующая максимуму кривой распределения энергии по длинам волн в спектре теплового излучения абсолютно чёрного тела, обратно… … Большой энциклопедический политехнический словарь

ВИНА ЗАКОН СМЕЩЕНИЯ — длина волны, на к рую приходится максимум энергии в спектре равновесного излучения, обратно пропорциональна абс. темп ре излучающего тела. Выведен в 1893 В. Вином … Естествознание. Энциклопедический словарь

Источник

Закон Стефана-Больцмана. Закон смещения Вина.

Законы Стефана— Больцмана и смещения Вина

Из закона Кирхгофа (см. (198.1)) следует, что спектральная плотность энергетической светимости черного тела является универсальной функцией, поэтому нахождение ее явной зависимости от частоты и температуры является важной задачей теории теплового излучения.

Австрийский физик Й. Стефан (1835— 1893), анализируя экспериментальные данные (1879), и Л. Больцман, применяя термодинамический метод (1884), решили эту задачу лишь частично, установив зависимость энергетической светимости R_e от температуры. Согласно закону Стефана — Больцмана,

(199.1)

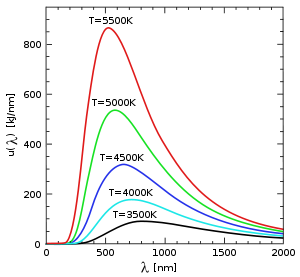
Закон Стефана — Больцмана, определяя зависимость R_eот температуры, не дает ответа относительно спектрального состава излучения черного тела. Из экспериментальных кривых зависимости функции 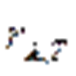от длины волны при различных температурах (рис. 287) следует, что распределение энергии в спектре черного тела является неравномерным.

Все кривые имеют явно выраженный максимум, который по мере повышения температуры смещается в сторону более коротких волн. Площадь, ограниченная кривой зависимости от и осью абсцисс, пропорциональна энергетической светимости R_e черного тела и, следовательно, по закону Стефана — Больцмана, четвертой степени температуры.

Немецкий физик В. Вин (1864—1928), опираясь на законы термо- и электродинамики, установил зависимость длины волны , соответствующей максимуму функции , от температуры Т. Согласно закону смещения Вина,

(199.2)

Несмотря на то, что законы Стефана — Больцмана и Вина играют в теории теплового излучения важную роль, они являются частными законами, так как не дают общей картины распределения энергии по частотам при различных температурах.

Формулы Рэлея — Джинса и Планка

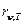
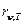
Из рассмотрения законов Стефана — Больцмана и Вина следует, что термодинамический подход к решению задачи о нахождении универсальной функции Кирхгофа r не дал желаемых результатов. Следующая строгая попытка теоретического вывода зависимости принадлежит английским ученым Д. Рэлею и Д. Джинсу (1877—1946), которые применили к тепловому излучению методы статистической физики, воспользовавшись классическим законом равномерного распределения энергии по степеням свободы.

Формула Рэлея — Джинса для спектральной плотности энергетической светимости черного тела имеет вид

(200.1)

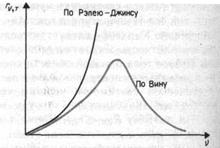
Как показал опыт, выражение (200.1) согласуется с экспериментальными данными только в области достаточно малых частот и больших температур. В области больших частот формула Рэлея — Джинса резко расходится с экспериментом, а также с законом Вина (рис. 288). Кроме того, оказалось, что попытка получить закон Стефана — Больцмана (см. (199.1)) из формулы Рэлея — Джинса приводит к абсурду. Действительно, вычисленная с использованием (200.1) энергетическая светимость черного тела (см. (198.3))

в то время как по закону Стефана — Больцмана R_eпропорциональна четвертой степени температуры. Этот результат получил название «ультрафиолетовой катастрофы». Таким образом, в рамках классической физики не удалось объяснить законы распределения энергии в спектре черного тела.

Правильное, согласующееся с опытными данными выражение для спектральной плотности энергетической светимости черного тела было найдено в 1900 г. немецким физиком М. Планком. Для этого ему пришлось отказаться от установившегося положения классической физики, согласно которому энергия любой системы может изменяться непрерывно, т. е. может принимать любые сколь угодно близкие значения. Согласно выдвинутой Планком квантовой гипотезе, атомные осцилляторы излучают энергию не непрерывно, а определенными порциями — квантами, причем энергия кванта пропорциональна частоте колебания (см. (170.3)):

(200.2)

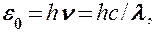
В данном случае среднюю энергию осциллятора нельзя принимать равнойkT. Вероятность, что осциллятор находится в состоянии с энергией пропорциональна , но при вычислении средних значений (при дискретных значениях энергии) интегралы заменяются суммами. При данном условии средняя энергия осциллятора

а спектральная плотность энергетической светимости черного тела

Таким образом, Планк вывел для универсальной функции Кирхгофа формулу

(200.3)

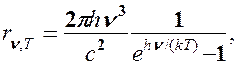
которая блестяще согласуется с экспериментальными данными по распределению энергии в спектрах излучения черного тела во всем интервале частот и температур. Теоретический вывод этой формулы М. Планк изложил 14 декабря 1900 г. на заседании Немецкого физического общества. Этот день стал датой рождения квантовой физики.

В области малых частот, т.е. при -8 .

Для реальных тел закон Стефана-Больцмана выполняется лишь качественно, то есть с ростом температуры энергетические светимости всех тел увеличиваются. Однако, для реальных тел зависимость энергетической светимости от температуры уже не описывается простым соотношением (16.7), а имеет вид:

. (16.11)

КоэффициентА(T) в (16.11), всегда меньший единицы, можно назвать интегральной поглощательной способностью тела. Значения коэффициентаА(T) известны для многих технически важных материалов. Так, в достаточно широком диапазоне температур для металловА(T) = 0,1 ÷ 0,4, а для угля и окислов металлов А(T) = 0,5 ÷ 0,9.

Энергетическая светимость 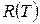АЧТ, численно равная площади под соответствующими кривыми, сильно зависит от температуры. Максимум излучательной способности с увеличением температуры смещается в сторону коротких длин волн.

Закон Стефана-Больцмана не дает информации о спектральном составе излучения абсолютно черного тела.

В 1893 г. немецкий физик В.Вин теоретически рассмотрел термодинамический процесс сжатия излучения, заключенного в полости с идеально зеркальными стенками, и пришел к выводу, что испускательная способность абсолютно черного тела прямо пропорциональна кубу частоты и является функцией отношения ν/T:

, (16.12)

Переходя в этой формуле Вина от частоты к длине волны, получим:

. (16.13)

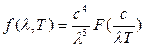
Как видно, в выражение для излучательной способности температура входит лишь в виде произведения λT. Уже это обстоятельство позволило предсказать некоторые особенности функции . В частности, эта функция достигает максимума при определенной длине волны λ_m, которая при изменении температуры тела изменяется так, чтобы выполнялось условие: λ_mT = const.

Таким образом, В. Вин сформулировал закон теплового излучения, согласно которому длина волны λ_m, на которую приходится максимум излучательной способности абсолютно черного тела, обратно пропорциональна его абсолютной температуре. Этот закон можно записать в виде

, (16.14)

где — постоянная Вина.

Закон Вина называют законом смещения, подчеркивая тем самым, что при повышении температуры абсолютно черного тела положение максимума его излучательной способности смещается в область коротких длин волн. Результаты экспериментов, приведенные на рис. 16.4, подтверждают этот вывод не только качественно, но и количественно, строго в соответствии с формулой (16.14).

С ростом температуры любого тела длина волны, вблизи которой тело излучает больше всего энергии, также смещается в сторону коротких длин волн. Это смещение, однако, уже не описывается простой формулой (16.14), которую для излучения реальных тел можно использовать только в качестве оценочной, т.е. формула (16.14) остается в силе только при больших частотах и низких температурах.

Кроме закона смещения (16.14) Вин получил выражение для максимального значения излучательной способности АЧТ. Эту зависимость называют вторым законом Вина, согласно которому максимальное значение испускательной способности АЧТпрямо пропорционально абсолютной температуре в пятой степени:

, (16.15)

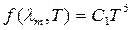
где . Однако, получить теоретическое выражение для универсальной функции Кирхгофа, хорошо описывающее экспериментальные результаты во всем диапазоне длин волн излучения тела, Вину не удалось.

Во всех разобранных выше случаях подход к изучению теплового излучения был термодинамическим. У.Рэлей и Д.Джинс впервые к этим явлениям применили методы классической статистической физики. Согласно закону о равномерном распределении энергии равновесной системы по степеням свободы на каждую колебательную степень свободы осциллятора с собственной частотой ν приходится энергия, равная = kT, где k −постоянная Больцмана. В соответствии с таким подходом У.Рэлей и Д.Джинс в 1905 г. получили выражение для универсальной функции Кирхгофа:

= kT. (16.16) Здесь − общее число степеней свободы системы, приходящихся на единицу объема полости.

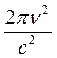
Однако, как показал опыт, формула Рэлея – Джинса хорошо согласуясь с опытными данными только для малых частот (рис.16.5) и больших температур, не удовлетворяет закону смещения Вина, а также закону Стефана-Больцмана. Действительно, для абсолютно черного тела энергетическая светимость R(T), определяемая по формуле Рэлея−Джинса (16.16), оказывается равной бесконечности:

.

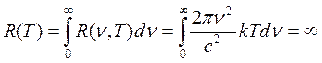
Согласно закону Стефана-Больцмана (1.10) энергетическая светимость т.е. является конечной величиной. Поскольку вывод формулы (16.16) был безупречным в своей классической строгости и последовательности, решение проблемы описания теплового излучения в рамках классической физики оказалось невозможным в принципе. Это обстоятельство получило в физике образное название «ультрафиолетовая катастрофа». Причина вышеуказанных трудностей, возникших при отыскании вида функции Кирхгофа, связана с одним из основных положений классической физики, согласно которому энергия любой системы может изменяться непрерывно, т.е. может принимать любые сколь угодно близкие значения.

Вопрос 5. Формула Планка.

Выход из создавшейся ситуации нашел немецкий физик М. Планк.

В 1900 г. он впервые выдвинул гипотезу о дискретных значениях энергии осциллятора.

, ( ). (16.17)

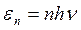
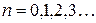
Согласно этой гипотезе Планк моделировал реальное твердое тело с помощью системы квантовых осцилляторов. Выполнив усреднение энергии осциллятора с помощью распределения Больцмана, Планк получил выражение для среднего значения энергии, приходящейся на одну колебательную степень свободы осциллятора:

. (16.18)

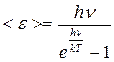
Подставив соотношение (16.18) в формулу Рэлея – Джинса (16.14), Планк получил формулу для излучательной способности АЧТ как функцию от частоты излучения:

. (16.19)

Эта формула как функция от длины волны излучения имеет вид:

, (16.20)

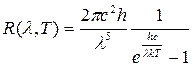
именно ее чаще всего используют в экспериментальных работах.

Из формулы Планка вытекают все законы теплового излучения тел.

В области малых частот, т.е. при условии, что квант энергии во много раз меньше средней энергии осциллятора (h , формула Планка совпадает с формулой Релея—Джинса. Для доказательства этого разложим функцию e h в ряд:

e h =1+ ) + ( ) +… (16.21)

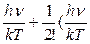
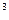
и, ограничившись первыми двумя членами разложения, из (16.19) получаем формулу Релея—Джинса (16.14):

R( = .

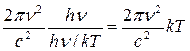
В предельном случае больших частот ( 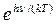>>1) единицей в знаменателе формулы (16.19) можно пренебречь, тогда получим формулу

, (16.22)

которая совпадает с выражением (16.12), т.е. с формулой Вина, причем, функция F(ν/Т) представляет собой выражение

,

которое действительно зависит от отношения частоты к температуре. График функции Вина показан на рис. 16.5. Функции Вина совпадает с формулой Планка только в области больших частот.

Интегральную излучательную способность АЧТ (закон Стефана—Больцмана) можно получить, проинтегрировав выражение (16.20) по длинам волн в интервале от 0 до :

. (16.23)

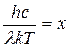
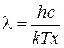
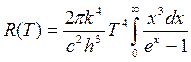
Произведем замену переменной. Обозначим , тогда подстановка и приводит выражение (16.21) к виду

, (16.24)

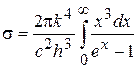
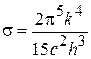
где . Так как , то

. (16.25)

Как видим, величина s (постоянная Стефана-Больцмана) выражается через постоянные величины c, h, k.

Анологично, исследуя функцию (16.22) по переменной ν на экстремум, можно получить значение постоянной Вина, которая выражается также через постоянные с, h и k, и выполнить проверку закона смещения Вина.

Таким образом, формула Планка не только хорошо согласуется с

экспериментальными данными, но и содержит в себе частные законы теплового излучения. Следовательно, формула Планка является полным решением основной задачи теплового излучения, поставленной Кирхгофом. Ее решение стало возможным лишь благодаря революционной квантовой гипотезе Планка.

Источник