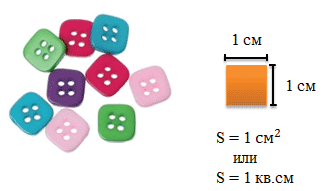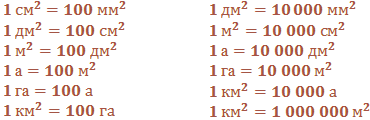в чем измеряется площадь поверхности
Единицы измерения площадей. Свойства площадей
Измерение площадей
Для измерения площадей используют такие единицы измерения:
квадратный сантиметр, квадратный дециметр, квадратный метр, квадратный километр
Квадратный сантиметр – это площадь квадрата со стороной в 1 см
Квадратный дециметр – это площадь квадрата со стороной в 1 дм
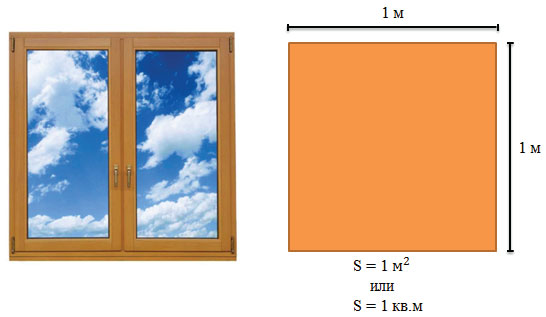
Квадратный метр – это площадь квадрата со стороной в 1 м
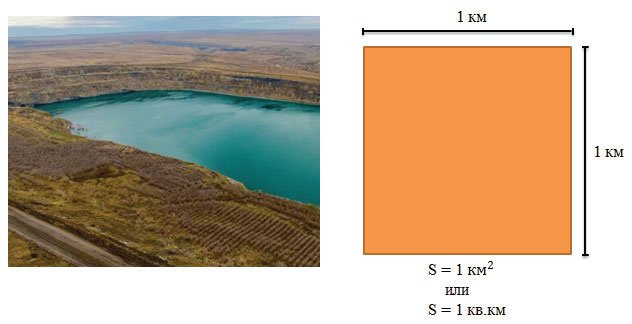
Для измерения больших площадей используют квадратный километр – это площадь квадрата, сторона которого равна 1 км
В квадратных километрах измеряют, например, площади городов (площадь Москвы 1091 км 2 )
Обозначают площадь заглавной буквой латинского алфавита S
Площади полей измеряют в гектарах (га).
Площади небольших участков земли измеряют в арах (а).
Соотношения между единицами измерения площадей
Если длина и ширина прямоугольника выражены, например, в метрах, то его площадь выражается в квадратных метрах.
Если длина и ширина прямоугольника измерены в разных единицах, то их надо выразить в одних единицах.
Свойства площадей
Поделись с друзьями в социальных сетях:
Площадь
Что такое площадь
Понятие площади фигур рассматривается одним из разделов математики — конкретно, геометрией. Результат решения задач с нахождением площади геометрических фигур может использоваться для решения математических задач, в быту, в производстве.
Площадь фигуры — численная характеристика, которая передает информацию о размере геометрической фигуры.
Фигура, в математическом мире определяемая как множество точек на плоскости, должна быть ограничена со всех сторон, чтобы иметь понятие площади. Если фигура располагается на одной плоскости, она не имеет объема, а только площадь.
В самом простом случае, площадь фигуры можно посчитать по количеству клеток, которые она занимает. Подобным способом можно легко посчитать площадь квадрата, прямоугольника или прямоугольного равнобедренного треугольника.
Площадь в геометрии обозначается знаком S, от английского square — площадь.
Как математическая характеристика, площадь имеет четыре характеристики:
Единицы измерения площади
Площадь фигуры может измеряться в разных единицах в зависимости от поверхности, на которой располагается. Основной системой измерения считается Международная система единиц СИ.
Площадь измеряется в единицах измерения в квадрате:
В Древней Руси употребляли такие величины, как квадратная верста, десятина, квадратный сажень.
В античных источниках единицей измерения площади были актус, арура, центурия, югер.
Формула нахождения площади в математике
Существует множество формул нахождения площади простых геометрических фигур, которые зависят, в основном, от количества углов, сторон и их соотношений.
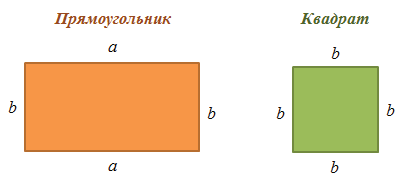
Площадь прямоугольника
Прямоугольником является геометрическая фигура, все углы которой равны 90°. При этом таких углов должно быть, как минимум три, а четвертый будет равен 90° в силу закона о сумме углов четырехугольника в евклидовой геометрии.
Вычисление площади прямоугольника будет происходить через умножение сторон:
где a и b являются сторонами прямоугольника.
Площадь квадрата
Квадратом является прямоугольник с равными сторонами. Все его углы равны 90°. Площадь квадрата можно найти сразу двумя способами:
По длине стороны:
Через диагонали:
где a — длина сторон квадрата;
d — длина диагоналей квадрата.
Площадь круга
Кругом является часть плоскости, которая лежит внутри окружности. Круг не имеет ни одного угла, а точки его окружности находятся на равном удалении от центра.
Площадь круга можно найти двумя способами:
Через радиус:
где π — постоянная Пи, равна 3,14.
Радиус, упоминаемый в формуле, является линией или отрезком, соединяющим центр и любую из точек окружности.
Через диаметр:
где π — постоянная Пи, равна 3,14.
Диаметр является отрезком, соединяющим две точки окружности и проходящим через центр. Он включает в себя два противоположно направленных радиуса.
Площадь эллипса
Эллипс является частным случаем окружности. Он, так же, как и круг, не имеет ни одного угла, но при этом точки окружности находятся на разном удалении от центра.
Найти площадь эллипса можно только одним способом: через произведение длин большой и малой полуосей эллипса и числа пи.
Площадь эллипса находится через произведение длин большой и малой полуосей эллипса и числа пи:
Площадь параллелограмма
Параллелограмм является геометрической фигурой с 4 углами и 4 сторонами, однако он отличается от прямоугольника по строению. Его противолежащие стороны попарно параллельны, а углы равны зеркально противолежащим.
Частными случаями параллелограмма являются квадрат, прямоугольник и ромб.
Найти площадь параллелограмма можно тремя способами:
Через сторону и высоту:
где a — сторона, к которой проведена высота,
h — высота непосредственно.
Через две стороны и величину угла между ними:
Через диагонали и угол между ними:
S = 1 2 × d 1 × d 2 × sin y
где d 1 и d 2 — это диагонали параллелограмма,
y — угол между ними.
Площадь ромба
Ромб, как частный случай параллелограмма, имеет те же свойства, кроме того, что все его стороны равны.
Площадь ромба также можно найти тремя способами:
По длине стороны и высоте:
Формула площади ромба по стороне и высоте выглядит так же, как и площадь параллелограмма по таким же характеристикам, с условием, что все высоты ромба будут равны:
По длине стороны и углу:
Формула площади ромба через длину сторон и углу между ними похожа на соответствующую формулу площади параллелограмма с условием того, что стороны равны, а значит, их перемножение можно заменить квадратом величины стороны:
По длине его диагоналей:
Площадь трапеции
Трапеция отличается от всех предыдущих фигур тем, что только две ее стороны, боковые, могут быть равны между собой. При этом они не параллельны. Две другие стороны параллельны, но не равны. Сумма углов трапеции равна 360°.
Площадь трапеции можно найти двумя способами:
По формуле Герона:
По длине основ и высоте:
Площадь треугольника
Треугольник является геометрической фигурой с тремя сторонами и суммой углов, равной 180°. По величине углов треугольники делятся на острые, тупые и прямоугольные. По числу равных сторон треугольники делятся на разносторонние, равносторонние и равнобедренные.
Площадь треугольника можно найти множеством способов:
По гипотенузе и острому углу:
a — любой из прилежащих острых углов.
Через сторону и высоту:
Через три стороны:
где р — полупериметр.
Через две стороны и угол между ними:
S = 1 2 × a × b × sin y
Через три стороны и радиус описанной окружности:
Через три стороны и радиус вписанной окружности:
где р — полупериметр.
Пояснения на примерах
Стены класса равны 7 и 5 метрам. Чему будет равна площадь пола в данной комнате?
Решение: S = 7 × 5 = 35
Ткань летучего змея порвалась. Вася решил сделать новую форму. Он посчитал, что длина жердей летучего змея равна 15 и 23 см. Форму какой площади нужно взять Васе с учетом того, что для припусков для пришивания нужно взять еще 2 см?
Равнобедренный треугольник имеет основание 4 дм и высоту 7 дм. Сколько будет его площадь?
Площадь
Рассмотрим фигуру ниже:
Вся фигура состоит из 8 квадратов со стороной 1 см каждый.
Площадь измеряется только в квадратных единицах длины. Всегда проверяйте свои ответы.
В математике для нахождения площади геометрических фигур используют специальные формулы, в которых площадь обозначается заглавной латинской буквой « S ».
Напоминаем, что площадь квадрата можно найти, умножив длину его стороны на саму себя.
Единицей площади служит площадь единичного квадрата. Например, если длина стороны квадрата, равна 1 м, то его площадь равна 1 квадратному метру ( 1 м 2 ); если длина его стороны равна 1 см, то его площадь равна 1 квадратному сантиметру ( 1 см 2 ).
Для нахождения площади какой-либо фигуры её сравнивают с единичным квадратом.
Как перевести квадратные единицы
Рассмотрим квадрат со стороной 1 см.
S = 1 см · 1 см = 1см 2
Рассмотрим квадрат со стороной 1 м.
S = 1 м · 1 м = 1 м 2
Известно, что: 1 м = 100 см
1 м 2 = 1 м · 1 м = 100 см · 100 см = 10 000 см 2
Увеличим сторону квадрата равную 1 м в 10 раз. Получим квадрат со
стороной 10 м.
Площадь такого квадрата называют ар или сотка.
S = 10 м · 10 м = 100 м 2
В одном аре — сто квадратных метров.
Слово «сотка» часто используют в дачном хозяйстве, хотя это тоже самое, что и «ар».
1 ар (сотка) = 100 м 2
Значит: 1 ар (сотка) = 100 м 2 = 100 · 10 000 см 2 = 1 000 000 см 2
Увеличим сторону квадрата равную 10 м в 10 раз. Получим квадрат со
стороной 100 м.
Площадь такого квадрата называют гектар. Сокращенно «га». Но при произношении вслух наименование проговаривается полностью.
Выразим гектар в квадратных метрах.
1 га = 100 м · 100 м = 10 000 м 2
Теперь определим, сколько в одном гектаре аров.
Значит: 10 000 м 2 : 100 м 2 = 100 (ар)
1 км 2 = 1 км · 1 км = 1 000 м · 1 000 м = 1 000 000 м 2
Для простоты расчётов предлагаем вам в помощь таблицу переводов квадратных единиц.
Таблица переводов квадратных единиц
Данная таблица поможет перевести гектары в кв. метры, гектары в ары и наоборот.
Какую ⚠️ единицу измерения используют при измерении площади
Периметр
Периметр – это замкнутая граница плоской геометрической фигуры, отделяющая её внутреннюю область от внешней.
Периметр есть у любой замкнутой геометрической фигуры:
На рисунке периметры выделены красной линией. Обратите внимание, что периметр окружности часто называют длиной.
Периметр измеряется в единицах измерения длины: мм, см, дм, м, км.
У всех многоугольников нахождение периметра сводится к сложению длин всех сторон, то есть периметр многоугольника всегда равен сумме длин его сторон. При вычислении периметр часто обозначают большой латинской буквой P :
Формулы площади трапеции
Формула Герона для трапеции S = a + b √(p-a )(p-b )(p-a-c )(p-a-d ) |a — b |
где S — площадь трапеции, a, b — длины основ трапеции, c, d — длины боковых сторон трапеции,
| p = | a + b + c + d | — полупериметр трапеции. |
| 2 |
Вы можете воспользоваться онлайн калькулятором для расчета площади трапеции.
Единицы измерения площади
Квадратом называется прямоугольник с равными сторонами.
В основе названий единиц измерения лежит понятие о квадрате. Площадь измеряется квадратными сантиметрами, дециметрами, метрами и километрами.
То есть, если мы решаем задачу с поиском площади фигуры, мы пишем см², дм², м², км², но произносим — квадратных сантиметров, квадратных дециметров, квадратных метров, квадратных километров.
Повторим и запомним перевод из одних единиц измерения в другие. 1 дм = 10 см. 1 дм² = 10 см * 10 см = 100 см². 1 м² = 100 дм². 1 м² = 10 000 см².
У прямоугольника две стороны: 5 см и 7 см. Найдите его площадь. Решение: 5 * 7 = 35 см² Ответ: Площадь прямоугольника составляет 35 см².
На конкурсе в честь дня города соревновались любители выпечки. В финале был представлен прямоугольный пирог с яблоком со сторонами 350 и 160 см. Размер прямоугольного пирога с тыквой составлял 45 дм². Какой пирог победил в конкурсе и почему. Решение:350 * 160 = 5600 см².5600/100 = 56 дм².56 дм² больше, чем 45 дм² — значит, победил пирог с яблоком. Ответ: 56 дм² > 45 дм², поэтому в конкурсе победил пирог с яблоком.
Обозначения
Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу
Например, вычислим площадь квадрат со стороной 2 см.
Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:
Вычислим площадь квадрата со стороной 3 метра
Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:
Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см
Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:
Объём геометрической фигуры
Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.
Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.
Измерить объём какой-нибудь фигуры означает выяснить сколько кубических единиц вмещается в данную фигуру.
Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:
Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:
Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см 3 ). Тогда объём V рассмотренного нами параллелепипеда равен 12 см 3
V = 12 см 3
Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
V = abc
где, a — длина, b — ширина, c — высота
Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.
Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:
Действительно, в исходный куб вмещается 27 кубиков длиной 1 см
Таким образом, объём куба вычисляется по следующему правилу:
Кубический дециметр. Кубический метр
Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах ( м 3 ). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах ( дм 3 ).
Другое название одного кубического дециметра – один литр.
1 дм 3 = 1 литр
Формулы площади эллипса

где S — Площадь эллипса, a — длина большей полуоси эллипса, b — длина меньшей полуоси эллипса. Вы можете воспользоваться онлайн калькулятором для расчета площади эллипса.
Площадь: определение, разновидности, единицы измерения
Площадь: определение, разновидности, единицы измерения.
Площадь (математический знак S)— величина, измеряющая размер поверхности. Наиболее распространенные единицы измерения площади это: квадратный метр (м2), квадратный сантиметр (см2), квадратный миллиметр (мм2), квадратный километр (км2), ар (а), гектар (га).
Площадь имеет следующие свойства:
1. положительность (число, получившееся в результате измерения площади не должно быть равно отрицательному числу);
2. нормировка (площадь измеряется в определенных единицах измерения);
3. равные фигуры имеют равную площадь;
4. площадь объединения двух фигур без общих внутренних точек равна сумме площадей.
Необходимость в измерении площади присутствует во всех сферах жизнедеятельности человека. Наиболее часто при этом пользуются понятиями: площадь фигуры и площадь поверхности.
Площадь фигуры (математический знак S)— геометрическое понятие, размер плоской фигуры. В простейшем случае, когда фигуру можно разбить на конечное множество квадратов, со стороной, равной одной единице измерения площади, площадь равна числу квадратов.
Площадь поверхности — числовая характеристика поверхности. В простом случае сумма всех площадей плоских фигур, представляющих собой грани пространственной фигуры.
Для записи результатов измерения обычно используют следующие единицы измерения площади: квадратный метр (м2), квадратный сантиметр (с м2), квадратный миллиметр (мм2)
Одной из разновидностей измерения площади поверхности является площадь участка – числовая характеристика земельного участка. Для обозначения результатов ее измерения используются такие единицы, как ар (а) и гектар (га).
Способ измерения площади:
Основой для измерения площади является единичный квадрат.
Единичный квадрат – это квадрат, со стороной, равной 1 единице измерения. Площадь единичного квадрата равна одной единице измерения площади, возведенной в квадрат (вторую степень).
Например. Возьмем квадрат со стороной, равной единице измерения 1 метр (м) и измерим его площадь. Для этого вычислим произведение двух его сторон, образующих между собой угол. То есть умножить 1 метр на 1 метр (1м х 1м). Получаем 1 квадратный метр (м2). Таким образом, площадь квадрата со стороной 1 метр равна 1 квадратный метр. Также, можно это перевести и в прочие единицы измерения: сантиметры, миллиметры, километры. Тогда площадь будет равна квадратным сантиметрам (см2),квадратных миллиметров (мм2), 0, 000001 квадратным километрам (км2).
Площадь фигуры (поверхности, участка) равна сумме единичных квадратов и их частей. Для простых фигур она равна только сумме единичных квадратов. Единица измерения площади при записи в этом случае тоже возводится в квадрат.
Единицы измерения площади:
Наиболее распространенные единицы измерения площади это: квадратный метр (м2), квадратный сантиметр (см2), квадратный миллиметр (мм2), квадратный километр (км2), ар (а), гектар (га).
Квадратный метр (м²) — единица измерения площади. 1 м² равен площади квадрата со стороной в 1 метр. Также эта единица измерения равна 0,000 001 квадратных километров (км²),квадратных сантиметров (см²), 0,000 1 гектара, 0,01 ара
Квадратный метр – одна из единиц системы СИ. Эта система носит полное название Международной десятичной системы единиц, но наиболее известна как система СИ или Метрическая система единиц измерения. Она основана на использовании метра и грамма, и является международно-признанной системой. Метрические единицы измерения широко используются по всему миру, как в научных целях, так и в повседневной жизни.
Однако, помимо квадратного метра, широко распространены и другие единицы измерения площади. Такие как:
Квадратный сантиметр (см2) — единица измерения пощади, равная в системе СИ 0,0001 квадратного метра (м2). В школьной практике для объяснения величины сантиметра используют такие подручные приблизительные меры, как две тетрадных клеточки, потому квадратный сантиметр может быть с легкостью изображен как совокупность 4 тетрадных клеток.
Квадратный миллиметр (от милли… и метр, мм2) — единица измерения площади равная 0, 000001 квадратным метрам (м2) или 0, 0001 квадратному сантиметру (см2). Во многих странах на чертежах, в том числе и в России, миллиметр является единицей измерения длины по умолчанию: если размеры указаны без единиц измерения, то это размеры в миллиметрах.
Квадратный километр (км²,) — единица измерения площади, кратная квадратному метру и равная 1.000.000 квадратным метрам (м2). Также он равен площади квадрата со стороной в 1 километр, 100 гектарам.
Ар (а, от лат. area — площадь, поверхность) — единица измерения площади в метрической системе (системе СИ), равная площади квадрата со стороной 10 м, то есть 100 квадратных метров (м2). Известна также как «сотка» или 0, 01 гектара. Ар – одна из основных единиц измерения площади небольших земельных участков.
В России гектар является основной единицей измерения площади сельскохозяйственной земли. На территории РСФСР (и впоследствии СССР) единица «гектар» была введена в практику после Октябрьской революции, вместо десятины. Для перевода использовалось соотношение 1 га = 11/12 десятины.