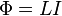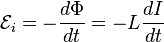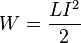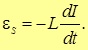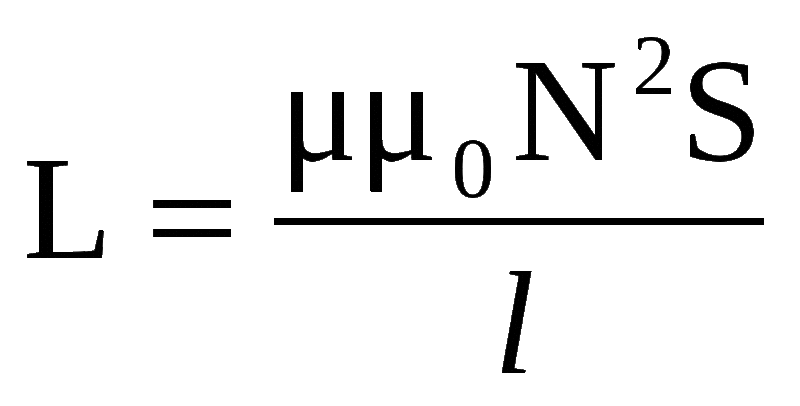в чем измеряется индуктивность контура
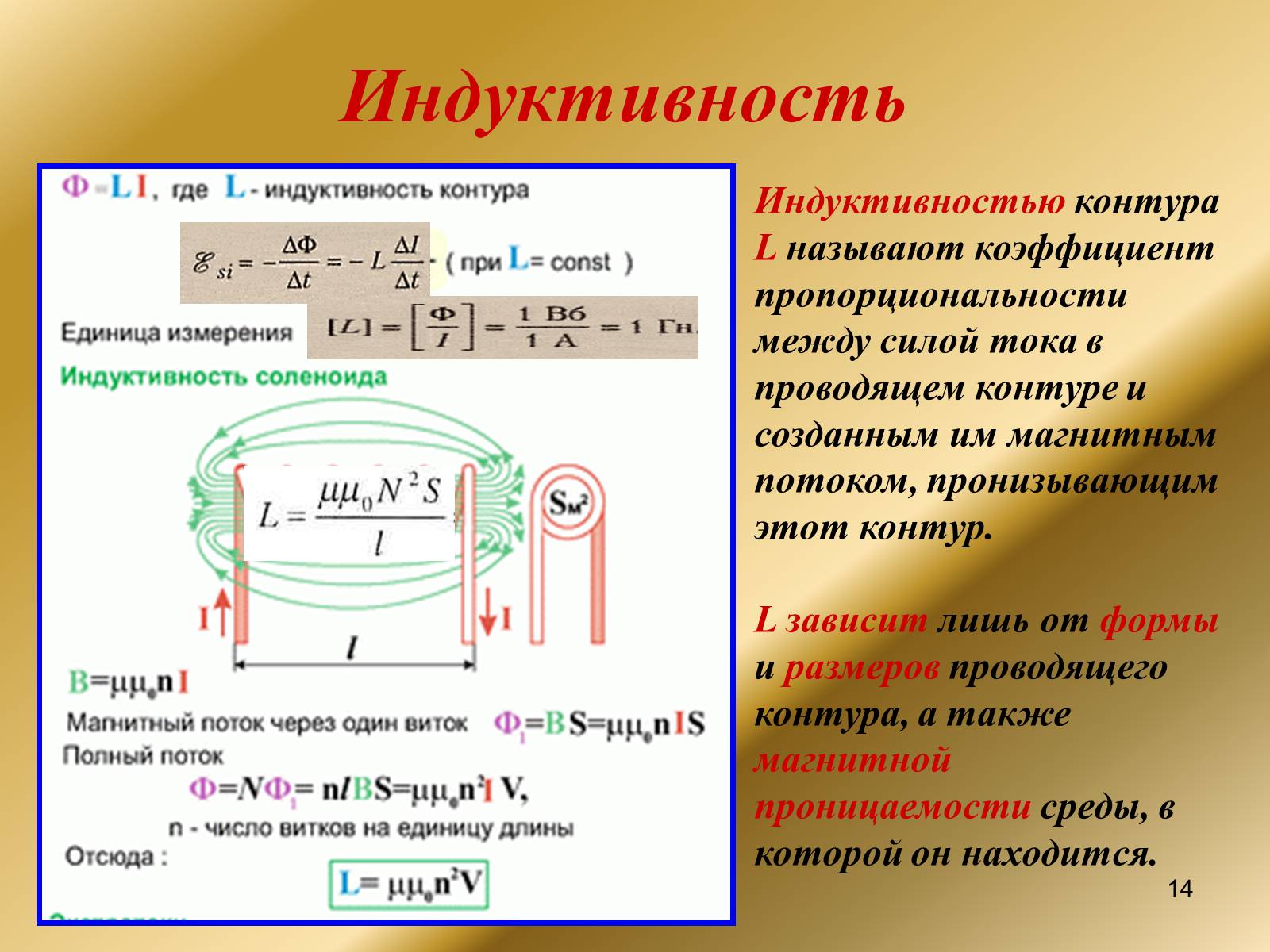
Индуктивность (коэффициент самоиндукции)
Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока:
Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.
При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током:
Практически участки цепи со значительной индуктивностью выполняют в виде катушек индуктивности. Элементами малой индуктивности (применяемыми для больших рабочих частот) могут быть одиночные (в том числе и неполные) витки или даже прямые проводники; при высоких рабочих частотах необходимо учитывать индуктивность всех проводников.
Для имитации индуктивности, т.е. ЭДС на элементе, пропорциональной и противоположной по знаку скорости изменения тока через этот элемент, в электронике используются и устройства, не основанные на электромагнитной индукции (см. Гиратор); такому элементу можно приписать определённую эффективную индуктивность, используемую в расчётах полностью (хотя вообще говоря с определёнными ограничивающими условиями) аналогично тому, как используется обычная индуктивность.
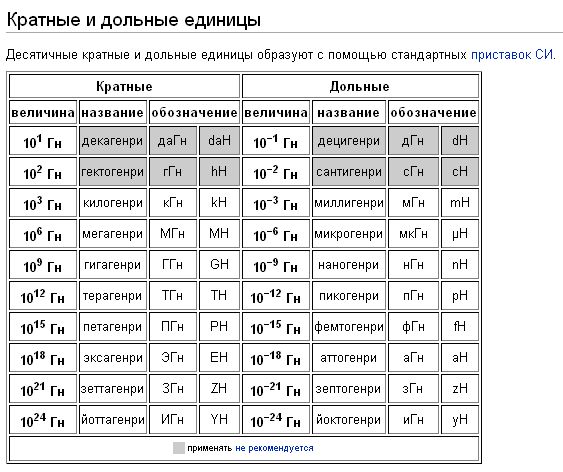
Обозначение и единицы измерения:
В системе единиц СИ индуктивность измеряется в генри, сокращённо Гн. Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт.
Символ L, используемый для обозначения индуктивности, был принят в честь Эмилия Христиановича Ленца (Heinrich Friedrich Emil Lenz). Единица измерения индуктивности названа в честь Джозефа Генри(Joseph Henry). Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года.
Материал из Википедии — свободной энциклопедии
Индуктивность
Выше мы рассматривали два основных понятия в электротехнике — идеальный генератор напряжения и идеальный генератор тока.
Идеальный генератор напряжения выдает заданное напряжения U (давление в водопроводной аналогии) на любой нагрузке (сопротивлении внешней цепи).
При этом в соответствии с законом Ома I=U/R, даже если R стремится к нулю, а ток возрастает до бесконечности.
Внутренне сопротивление идеального генератора напряжения равно 0.
Идеальный генератор тока выдает заданный ток I (поток в водопроводной аналогии), даже если сопротивление внешней цепи стремится к бесконечности. Напряжение на нагрузке при этом также стремится к бесконечности U=I*R.
Внутреннее сопротивление идеального генератора тока равно ∞.
Тут можно увидеть определенную симметрию, дуализм.
Мы рассматривали конденсатор С который может накапливать заряд (потому и называется — емкость) С=Q/U. Чем больше емкость, тем медленнее растет напряжение (давление) при закачке в конденсатор заряда U=Q/C.
Если емкость заряда очень большая (стремится к бесконечности), то такой конденсатор бесконечной емкости будет являться идеальным генератором напряжения. Он никогда не разрядится и при этом может выдать ток любой величины, и напряжение на нем будет оставаться постоянным.
Симметричным (дуальным) к конденсатору элементом будет являться индуктивность. Индуктивность обозначается буквой L (см схему ниже).
Обычно сам электронный компонент называется катушка индуктивности, а его параметр — индуктивность L.

Если конденсатор является генератором напряжения, то индуктивность является генератором тока. Индуктивность стремиться поддерживать ток в цепи постоянным, то есть препятствует изменению тока в цепи.
Индуктивность бесконечной величины является идеальным генератором тока, то есть будет бесконечно гнать заданный ток I независимо от сопротивления нагрузки.
Это похоже как если вы подойдете к стоящей на рельсах вагонетке и станете ее толкать (приложите к ней силу). Вагонетка начнет медленно разгоняться и «ток все быстрее и быстрее побежит по проводам». А потом попробуйте вагонетку тормозить и она будет медленно останавливаться.
Так и в индуктивности, после подачи напряжения ток будет постепенно расти (вагонетка разгоняется), а при подаче напряжения другой полярности — постепенно уменьшаться (вагонетка тормозится).
Отсюда следует вывод «Поезд мгновенно остановить нельзя!»
«Ток в индуктивности мгновенно остановить нельзя!»
То есть даже если щелкнуть выключателем S4 на схеме и разомкнуть цепь, ток в первый момент после этого будет продолжать идти! На практике это приводит к тому, что в момент размыкания контактов в выключателе между ними будет проскакивать искра.
Сопротивление при размыкании контактов увеличивается до бесконечности (в реальности до очень больших величин) и протекающий ток создаст на этом сопротивлении напряжение очень большой величины, так что воздушный промежуток между контактами будет пробит.
“При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС. Это явление называется самоиндукцией. Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током). Явление самоиндукции проявляется в замедлении процессов исчезновения и установления тока.”
Тут есть некий момент — постоянный ток это ток, который не меняется со временем, то, что называется «постоянная составляющая» частотой равной 0 Гц. Ее конденсатор не пропускает. Совсем.
А вот индуктивность совсем не пропускает переменный ток бесконечной частоты. А просто переменный ток любой конечной частоты немножко пропускает.
Но к понятию напряжения переменного тока мы вернемся позже.

При подаче на индуктивность постоянного напряжения ток в ней линейно возрастает со временем.
Мы помним аналогичную картину для конденсатора.
Напряжение на конденсаторе линейно возрастает при его заряде постоянным током.
А что будет, если запитать индуктивность от генератора тока?

Ну тут из серии «кто кого заборет — слон или кит».
Цепи, содержащие конденсатор и индуктивность
Как было отмечено выше, индуктивность в электротехнике играет ту же роль, что масса в механике. А что является аналогом конденсатора в механике? Конденсатор является генератором напряжения, то есть создает силу, которая двигает поток заряда по проводам. Выше мы приводили аналог конденсатора в виде водонапорной башни, которая заполняется водой (зарядом) и давление (напряжение) в ней увеличивается.
Но можно также представить конденсатор в виде пружины — при заряде пружина сжимается и сила сжатия (напряжение) увеличивается. Емкость в этом случае величина обратная жесткости пружины. Чем пружина жестче, тем быстрее возрастает сила при сжатии. То есть соединение конденсатора и индуктивности эквивалентно вагонетке закрепленной на пружине. )
Что же будет происходить, если конденсатор соединить с индуктивностью, например как в схеме на рис. 16

Пусть конденсатор С заряжен до напряжения U. Ключ S2 замыкается и в цепи начинает течь ток. Это эквивалентно тому, как если бы мы сжали пружину и затем в какой-то момент отпустили (замкнули ключ S2).
То есть цепь пришла в состояние когда конденсатор заряжен, ток в ней равен нулю.
Хм.. но это то же состояние, с которого мы начали, только полярность напряжения противоположная. Следовательно процесс повторится, только ток потечет уже в другую сторону и система вернется в исходное состояние. Вагонетка поедет обратно, проедет положение равновесия и по инерции снова сожмет пружину.
Возникнет колебательный процесс. То есть вагонетка на пружине так и будет кататься туда-сюда и в отсутствие потерь энергии (трения) этот процесс будет длиться бесконечно.
Таким образом соединение конденсатора с индуктивностью образует колебательное звено. Такие звенья широко используются в электротехнике для создания генераторов и фильтров напряжения переменного тока.
Понятие переменного тока рассмотрим в следующей статье.
UPD.
Поскольку возник диспут экспоненциально ли растет ток при подключении катушки индуктивности к генератору напряжения или линейно, скажу еще пару слов по этому вопросу.
Откуда же берется экспонента роста тока в схеме на рис.13?
Ответ- ниоткуда. Ее там нет. Ток растет линейно и зависимость тока от напряжения описывается формулой
ЭДС самоиндукции в цепи прямо пропорциональна скорости изменения силы тока в этой цепи.
Чтобы обеспечить U=const (а U – это производная от тока в катушке), ток должен линейно расти.
А откуда тогда вообще зашел разговор об экспоненте? А зашел он потому, что ток линейно растет только в идеальном случае — в схеме с идеальным генератором напряжения (бесконечной мощности и с нулевым внутренним сопротивлением) и идеальной индуктивностью (с нулевым внутренним сопротивлением).
В реальном случае с учетом внутреннего сопротивления схема будет выглядеть так.

На схеме рис.17 R символизирует собой внутреннее сопротивление генератора и катушки индуктивности. (они все равно включены последовательно, поэтому можно обойтись одним R, как суммой этих сопротивлений)
Вот в этом случае и получится такой экспоненциальный график роста тока в индуктивности.


зы. В интернете столько разнообразной ереси на тему катушек индуктивности. Просто диву даешься.
«Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение. Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения.»
Ну.. поскольку про резистор в цепи ничего не сказано, то не на короткий промежуток, а пока входное напряжение не будет снято. Вторая часть звучит бредово, но направление верное — ток с цепи растет от нуля до.. без резистора до бесконечности, с резистором до I=Uвх/R.
Предположим, что обычная катушка индуктивности подключена к источнику напряжения через ключ. При замыкании ключа на индуктивность подается напряжение, вызывающее быстрое изменение протекающего через нее тока. Когда приложенное напряжение увеличивается от нуля до пикового значения (за короткое время), индуктивность противодействует изменяющемуся через нее току, индуцируя напряжение, противоположное по полярности приложенному напряжению. Индуцированное напряжение при подаче питания на катушку индуктивности называется обратной ЭДС и определяется по формуле 1:
VL = – L*(di/dt), (1)
где:
VL – напряжение (обратная ЭДС), индуцированная на катушке;
L – индуктивность катушки;
di/dt – скорость изменения тока во времени.
Видимо здесь попытались описать начальный момент возникновения ЭДС самоиндукции, но получилась ерунда. Говорить, что «индуцированное напряжение противоположно по полярности приложенному напряжению» это то же самое, что «падение напряжения на резисторе противоположно по полярности приложенному напряжению.» Ага, точно, приложенное напряжение сложили с падением напряжения и после резистора получили 0. Так и есть, лол.
«ЭДС самоиндукции» в катушке это аналог «падения напряжения» на резисторе. Только в резисторе электрическая энергия рассеивается, переходит в тепло, а в индуктивности — накапливается, переходит в энергию магнитного поля. В водопроводной аналогии индуктивность это такая турбинка, вставленная в водопроводную трубу, и которая имеет момент инерции. Турбинка пропускает воду только когда вращается. И вот крантель открыли, давление к турбинке приложили, она начала вращаться и пошел ток дальше по трубе. И чем быстрее турбинка вращается, тем больше ее пропускная способность. Турбинка раскручивается, ток возрастает и так до бесконечности. Это если нет потерь энергии — резистора. А если есть резистор (трение), то часть давления расходуется на преодоление трения. И когда вся входная энергия будет расходоваться на трение, турбинка перестанет ускоряться и ток достигнет максимальной величины.

Картинка неправильная. В правильном варианте при отключении источника, подключался резистор и цепь оставалась замкнутой.
Рассмотрим следующую цепь

Вопрос на засыпку: Чему будет равно напряжение на индуктивности в первый момент после переключения ключа S из верхнего положения в нижнее?
Hint: Не надо выносить себе мозг, пытаясь сообразить с каким там знаком возникнет ЭДС самоиндукции и что с ней будет дальше. Надо применять простое правило:
Ток в индуктивности в первый момент времени после переключения сохраняется неизменным.
Дальше применять закон Ома.
Индуктивность: формула
Введение
Если бы кому-нибудь пришла в голову идея провести опрос населения Земли на тему «Что вы знаете об индуктивности?», то подавляющее число опрашиваемых просто пожало бы плечами. А ведь это второй по многочисленности вслед за транзисторами технический элемент, на котором зиждется современная цивилизация! Любители детективов, припомнив, что в своей юности зачитывались захватывающими рассказами сэра Артура Конан Дойла о приключениях знаменитого сыщика Шерлока Холмса, с разной степенью уверенности пробормочут что-то о методе, которым вышеозначенный сыщик пользовался. При этом подразумевая метод дедукции, который, наравне с методом индукции, является основным методом познания в западной философии Нового времени.
При методе индукции происходит исследование отдельных фактов, принципов и формирование общих теоретических концепций на основе полученных результатов (от частного к общему). Метод дедукции, наоборот, предполагает исследование от общих принципов, законов, когда положения теории распределяются на отдельные явления.
Следует отметить, что индукция, в смысле метода, не имеет сколько-нибудь прямого отношения к индуктивности, просто они имеют общий латинский корень inductio — наведение, побуждение — и обозначают совершенно разные понятия.
Лишь малая часть опрашиваемых из числа носителей точных наук — профессиональных физиков, инженеров-электротехников, радиоинженеров и студентов этих направлений — смогут дать внятный ответ на этот вопрос, а некоторые из них готовы прочитать с ходу целую лекцию на эту тему.
В физике индуктивность, или коэффициент самоиндукции, определяется как коэффициент пропорциональности L между магнитным потоком Ф вокруг проводника с током и порождающим его током I или — в более строгой формулировке — это коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током:
Для понимания физической роли катушки индуктивности в электрических цепях можно использовать аналогию формулы энергии, запасаемой в ней при протекании тока I, с формулой механической кинетической энергии тела.
При заданной силе тока I индуктивность L определяет энергию магнитного поля W, создаваемого этим током I:
Аналогично, механическая кинетическая энергия тела определяется массой тела m и его скоростью V:
То есть индуктивность, подобно массе, не позволяет энергии магнитного поля мгновенно увеличиться, равно как и масса не позволяет проделать такое с кинетической энергией тела.
Проведём исследование поведения тока в индуктивности:

Рис. 2. Физическая реализация эксперимента
Рис. 3. Осциллограмма тока через индуктивность. Желтая осциллограмма — выход сигнал-генератора, голубая — сигнал на резисторе.
Из-за инерционности индуктивности происходит затягивание фронтов входного напряжения. Такая цепь в автоматике и радиотехнике называется интегрирующей, и применяется для выполнения математической операции интегрирования.
Проведём исследование напряжения на катушке индуктивности:

Рис. 6. Осциллограмма напряжения на индуктивности (голубая)
В моменты подачи и снятия напряжения из-за присущей катушкам индуктивности ЭДС самоиндукции, возникают выбросы напряжения. Такая цепь в автоматике и радиотехнике называется дифференцирующей, и применяется в автоматике для корректировки процессов в управляемом объекте, носящих быстрый характер.
Рис. 5. По большому счёту, во всех генераторах электрического тока любого типа, равно как и в электродвигателях, их обмотки представляют собой катушки индуктивности.
Общие сведения
Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.

Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.
Среди основных свойств индуктивности выделяются:
Индуктивность соленоида
Катушка в форме соленоида (конечной длины).
где V=Sl <\displaystyle V=Sl>− объём катушки. Отсюда следует формула для индуктивности соленоида (без сердечника):
Если катушка внутри полностью заполнена магнитным материалом (сердечником), то индуктивность отличается на множитель μ <\displaystyle \mu >— относительную магнитную проницаемость сердечника:
В случае, когда μ>>1<\displaystyle \mu >>1>, можно (следует) под S понимать площадь сечения сердечника и пользоваться данной формулой даже при толстой намотке, если только полная площадь сечения катушки не превосходит площади сечения сердечника во много раз.
Одновитковой контур и катушка
Индуктивность контура, представляющего виток провода, зависит от величины протекающего тока и магнитного потока, пронизывающего контур. Для индуктивности контура формула определяет параметр, соответственно, через поток и силу тока:
Ослабление магнитного потока из-за диамагнитных свойств окружающей среды снижает индуктивность.
Параметр для многовитковой катушки пропорционален квадрату количества витков, поскольку увеличивается не только магнитный поток от каждого витка, но и потокосцепление:
Для того чтобы рассчитать индуктивность катушки формула должна учитывать не только количество витков, но и тип намотки и геометрические размеры.
Индуктивность и конденсатор
Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:

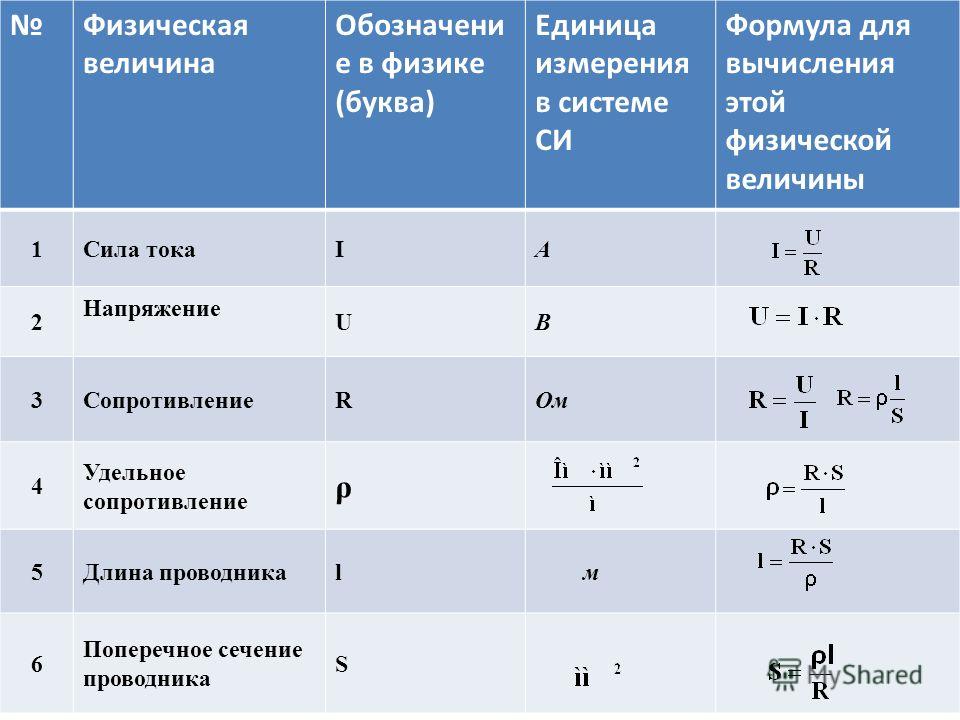




где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f – это частота, L – индуктивность.
Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.
Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:
где Lk показывает индуктивность устройства, Lp –пакета, Lm – главных шин, а Lb – индуктивность выводов.
Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:
Lk = Lc : n + µ0 l х d : (3b) + Lb,
где l – длина шин, b – ее ширина, а d – расстояние между шинами.
Индуктивность соленоида
Катушка в форме соленоида (конечной длины).
где V=Sl <\displaystyle V=Sl>− объём катушки. Отсюда следует формула для индуктивности соленоида (без сердечника):
Если катушка внутри полностью заполнена магнитным сердечником, то индуктивность отличается на множитель μ <\displaystyle \mu >— относительную магнитную проницаемость сердечника:
В случае, когда μ>>1<\displaystyle \mu >>1>, под S можно понимать площадь сечения сердечника и пользоваться данной формулой даже при толстой намотке, если только полная площадь сечения катушки не превосходит площади сечения сердечника во много раз.
Применение катушек в технике
Явление электромагнитной индукции известно уже давно и широко применяется в технике. Примеры использования:
Самоиндукция и измерение индуктивности
Индуктивностью называется величина, которая равна отношению магнитного потока, проходящего по всем виткам контура к силе тока:
Индуктивность контура находится в зависимости от формы, размеров контура и от магнитных свойств среды, в которой он находится. Если в замкнутом контуре протекает электрический ток, то возникает изменяющееся магнитное поле. Это впоследствии приведет к возникновению ЭДС. Рождение индукционного тока в замкнутом контуре носит название «самоиндукция». По правилу Ленца величина не дает изменяться току в контуре. Если обнаруживается самоиндукция, то можно применять электрическую цепь, в которой параллельно включены резистор и катушка с железным сердечником. Последовательно с ними подсоединены и электрические лампы. В этом случае сопротивление резистора равно сопротивлению на постоянном токе катушки. Результатом будет яркое горение ламп. Явление самоиндукции занимает одно из главных мест в радиотехнике и электротехнике.
Индуктивное сопротивление – как его найти
Реальная катушка имеет не только реактивное, но и обычное сопротивление. Индуктивное сопротивление определяется по формуле:
Здесь употреблены следующие обозначения:
Надо отметить, что величина (2*П*v) представляют собой круговую частоту, которую обозначают греческим символом «омега».
Катушки с различными сердечниками
Рассматриваемая величина подчиняется закону Ома. Формула выглядит так:
I, U представляют собой ток и напряжение, XL – это индуктивное сопротивление.
Конфигурация магнитного поля катушки
Для определения искомой величины можно воспользоваться приведенными формулами. При этом можно воспользоваться амперметром и вольтметром. Первый из них надо включить последовательно, второй — параллельно.







При этом необходимо учитывать следующее. На самом деле, в цепи, в которую включена индуктивность, действует два вида сопротивления: активное и реактивное. Измерив ток и напряжение, можно определить их результирующую величину. Нужно помнить, что она не является их простой суммой.
Дело в том, что в переменной цепи, где имеется только катушка и нет конденсатора, напряжение находится впереди тока на четверть периода колебания. Эта величина равна 90 градусам.
Полное сопротивление определяется следующим образом. Для этого необходимо нарисовать соответствующую диаграмму. Если по горизонтали отложить величину обычного, а по вертикали — реактивного, а затем по этим векторам построить прямоугольник, то длина его диагонали будет равна полному значению.
Магнитное поле провода
К примеру, если подобрать элементы цепи таким образом, чтобы по абсолютной величине обе этих величины были равны, то искомая часть определится как их полное значение, умноженное на квадратный корень из двух.
Для того, чтобы получить информацию о зависимости индуктивного сопротивления от частоты, возможно воспользоваться осциллографом.
При использовании переменного тока необходимо учитывать не только обычное, но и индуктивное сопротивление. Оно возникает в том случае, если в электрической цепи присутствует катушка.
Индуктивность, ее единица си. Индуктивность длинного соленоида.
—магнитный поток, — ток в контуре, — индуктивность.
Нередко говорят об индуктивности прямого длинного провода(см.). В этом случае и других (особенно — в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.
Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока :
Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.
При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током :
Колебательный контур
Емкость и индуктивный элемент, соединенные в цепь, образуют колебательный контур с резко выраженными частотными свойствами и будут являться резонансной системой. В качестве системы используется конденсатор, изменяя емкость которого, можно производить коррекцию частотных свойств.
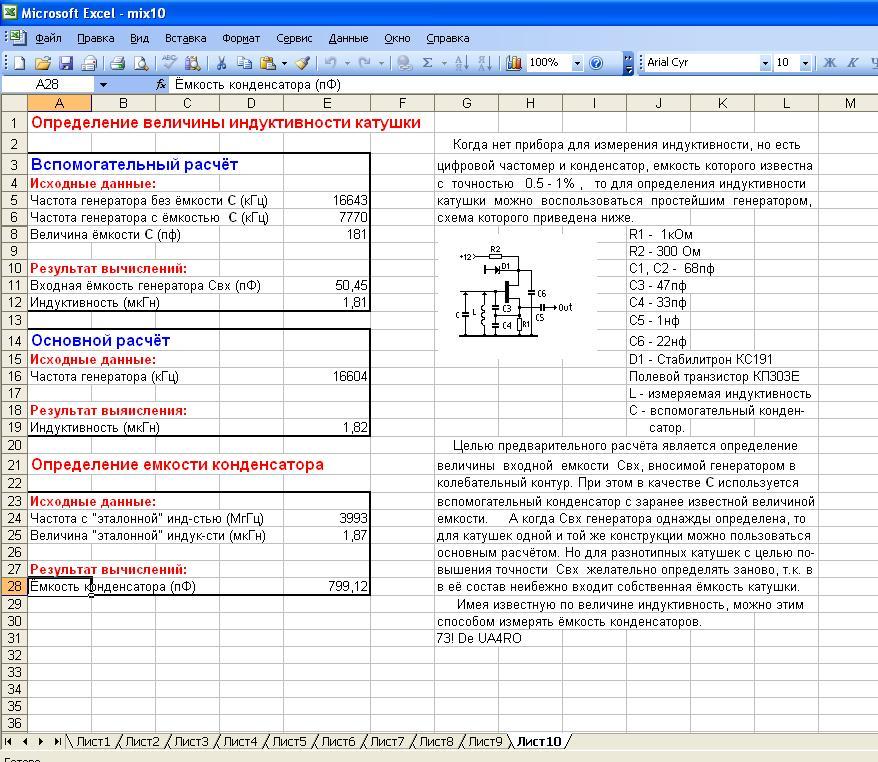
Если измерить резонансную частоту, используя известный конденсатор, то можно определить индуктивность катушки.
Индуктивность – важнейший элемент в разных областях электротехники. Для правильного применения нужно знать все параметры используемых элементов.
Устройство, которое позволяет определить параметры катушек индуктивности, в том числе добротность, может называться L-метр или Q-метр.
Как произвести пересчет катушек индуктивности (однослойных, цилиндрических)
Необходимость в пересчете катушек индуктивности возникает при отсутствии нужного диаметра провода, указанного в описании конструкции, и замене его проводом другого диаметра; при изменении диаметра каркаса катушки.
Если отсутствует провод нужного диаметра, что является наиболее частой причиной пересчета катушек, можно воспользоваться проводом другого диаметра.
Изменение диаметра провода в пределах до 25% в ту или другую сторону вполне допустимо и в большинстве конструкций не отражается на качестве их работы. Более того, увеличение диаметра провода допустимо во всех случаях, так как оно уменьшает омическое сопротивление катушки и повышает ее добротность.
Уменьшение же диаметра ухудшает добротность и увеличивает плотность тока на единицу сечения провода, которая не может быть больше определенной допустимой величины.
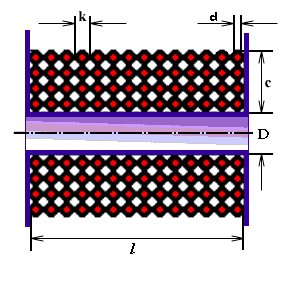
Пересчет числа витков однослойной цилиндрической катушки при замене провода одного диаметра другим производится по формуле:
В качестве примера произведем пересчет числа витков катушки, изображенной на рис. 1, для провода диаметром 0,8 мм:
(длина намотки l= 18 X 0,8 = 14,4 мм, или 1,44 см).
Таким образом, число витков и длина намотки несколько уменьшились. Для проверки правильности пересчета рекомендуется выполнить новый расчет катушки с измененным диаметром провода:
При пересчете катушки, связанном с изменением ее диаметра, следует пользоваться процентной зависимостью между диаметром и числом витков катушки.
Эта зависимость заключается в следующем: при увеличении диаметра катушки на определенное число процентов количество витков ее уменьшается на столько же процентов, и, наоборот, при уменьшении диаметра увеличивается число витков на равное число процентов. Для упрощения расчетов за диаметр катушки можно принимать диаметр каркаса.









Рис. 2. Катушки индуктивности. Пример.
Так, для примера произведем пересчет числа витков катушки (рис. 2, а), имеющей диаметр 1,5 см, на диаметр, равный 1,8 см (рис. 2, б). Согласно условиям пересчета диаметр каркаса увеличивается на 3 мм, или на 20%.
Следовательно, для сохранения неизменной величины индуктивности этой катушки при намотке ее на каркасе большего диаметра нужно уменьшить число витков на 20%, или на 8 витков. Таким образом, новая катушка будет иметь 32 витка.
Проверим пересчет н установим погрешность, допущенную в результате пересчета. Катушка (см. рис. 2, а) имеет индуктивность:
Новая катушка на каркасе с увеличенным диаметром:
Ошибка при пересчете составляет 0,25 мкГн, что вполне допустимо для расчетов в радиолюбительской практике.
Индуктивность прямолинейного провода круглого сечения
При расчёте индуктивности необходимо разделять индуктивность на постоянном токе и индуктивность на высокой частоте. Под высокой частотой следует понимать такую частоту, на которой толщина скин-слоя меньше размеров поперечного сечения провода. В случае если толщина скин-слоя больше поперечных размеров провода, то можно вести расчёт для постоянного тока.
В случае постоянного тока или тока низкой частоты индуктивность составит
где μ – магнитная постоянная, μ = 4π•10-7 Гн/м;
l – длина провода, м;
d – диаметр провода, м.
Как я уже говорил, на величину индуктивности влияет частота переменного тока, поэтому в случае необходимости рассчитать индуктивность на любой частоте применяется следующее выражение
где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Данный коэффициент зависит от величины k*r, где
d = 2r – диаметр поперечного сечения провода, м.
где ω – угловая частота переменного тока, ω = 2πf;
μ – магнитная постоянная, μ = 4π•10-7 Гн/м;
γ – удельная проводимость вещества проводника.
Пример. Необходимо рассчитать индуктивность прямолинейного провода круглого сечения из меди (γ = 5,81*107 См/м) диаметром d = 2 мм и длиной l = 4 м, при постоянном токе и токе частотой f = 50 кГц.






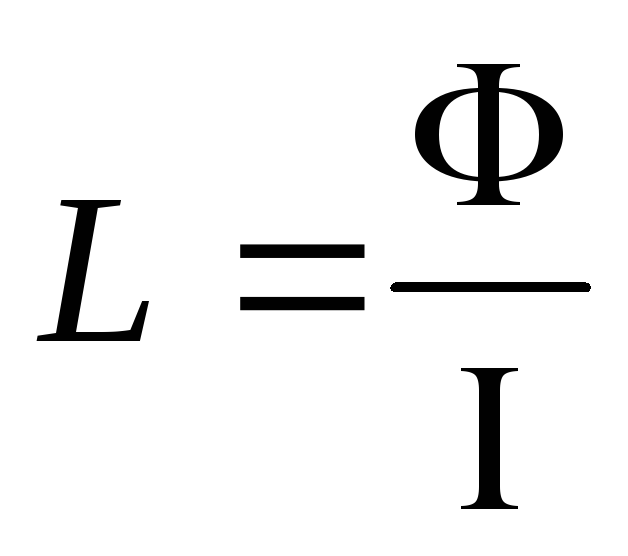
На постоянном токе
Способы расчёта
Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.
Через силу тока
Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:
Соленоид конечной длины
Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:
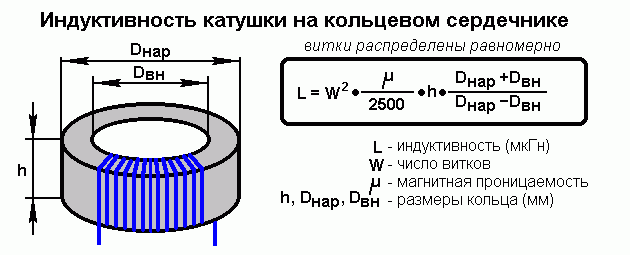
Катушка с тороидальным сердечником
В большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:
Длинный проводник
Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:
В чем измеряется индуктивность катушки
Понятие индуктивности. Единицы измерения. Катушки индуктивности. (10+)
Индуктивность. Понятие. Единицы измерения
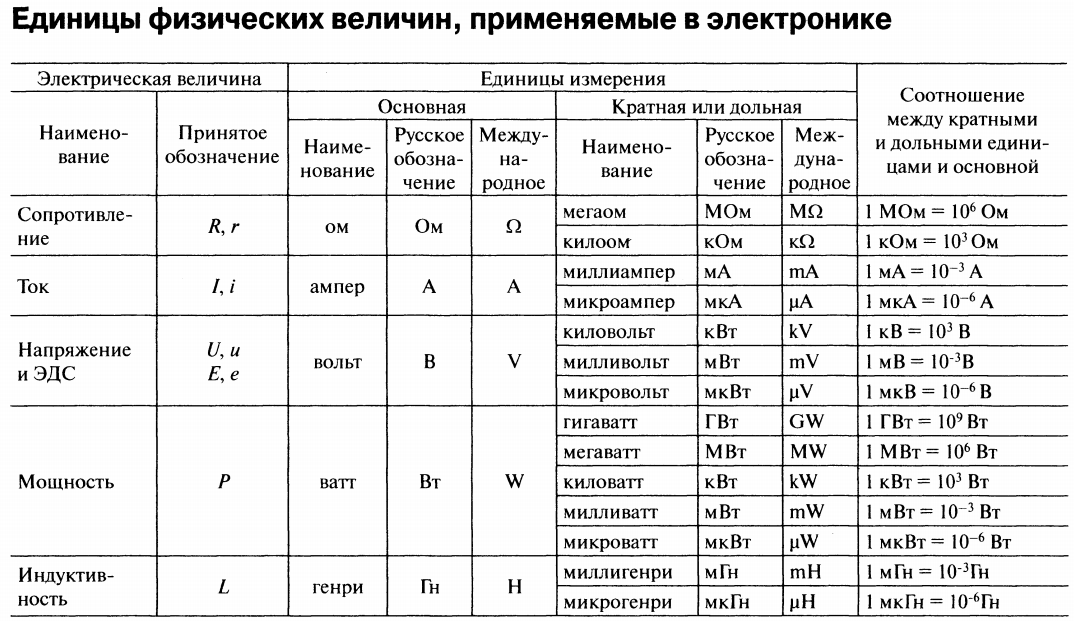
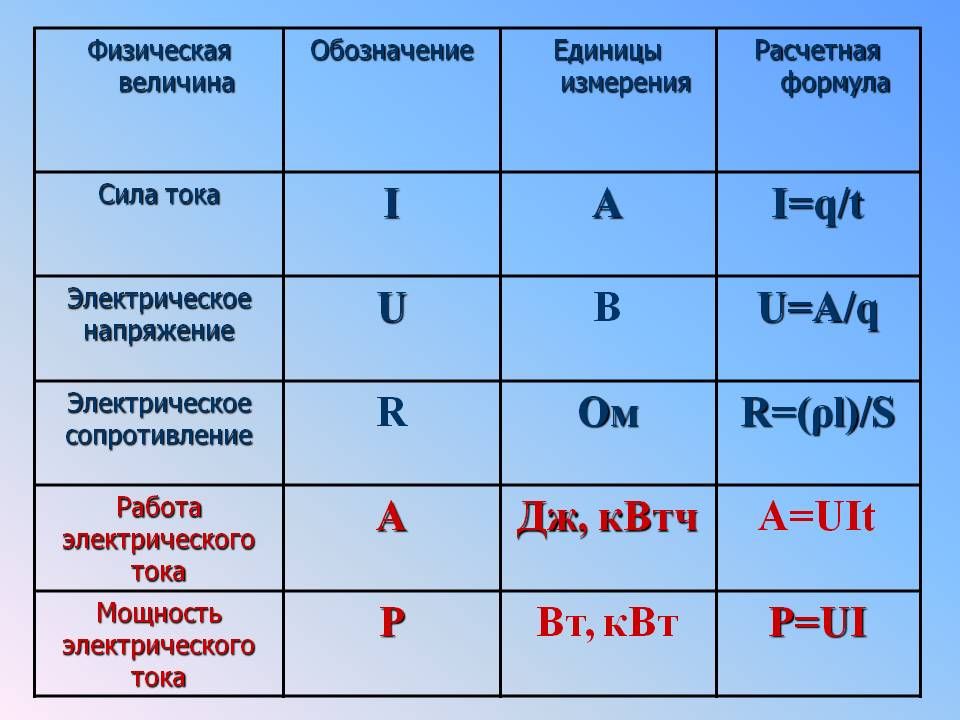
Материал является пояснением и дополнением к статье:Единицы измерения физических величин в радиоэлектронике Единицы измерения и соотношения физических величин, применяемых в радиотехника.
В самом начале изучения электричества исследователи заметили, что мотки провода при подаче на них напряжения ведут себя странно. Сила тока через них не подчиняется классическому закону Ома. Электрический ток не возникает сразу после подачи напряжения, а нарастает постепенно со временем. Прекратить этот ток тоже непросто. При разрыве цепи возникает искра в месте разрыва. Создается впечатление, что электрический ток в мотке провода обладает инерцией. Теоретические изыскания подтвердили это наблюдение. В катушках индуктивности после подачи на них напряжения происходит накопление энергии в магнитном поле и постепенный рост электрического тока. Если внешний источник отключить, то катушка продолжает поддерживать на своих вывода напряжение достаточное для постепенного убывания силы тока по мере исчерпания накопленной энергии. Если в цепи разрыв, то скачек напряжения может быть очень большим. Теоретические он должен быть бесконечным, но на практике либо происходит пробой места разрыва или изоляции самой катушки, либо вся энергия поглощается паразитными емкостями между витками.
Добротность катушки
Одно из важнейших качеств катушек – это добротность. Данный параметр представляет собой отношение реактивного (индуктивного) сопротивления к активному. Активное сопротивление – это сопротивление проводника, из которого выполнен элемент, его можно считать постоянным, за исключением температурного коэффициента сопротивления материала, из которого выполнен провод.
Реактивное сопротивление прямо пропорционально частоте. Формула расчета добротности выглядит следующим образом:
Обратите внимание! С ростом частоты сигнала добротность катушки индуктивности возрастает
Работа на постоянном и переменном токе
Магнитное поле, которое создается внутри катушки, направлено вдоль оси, и равно:
где µ0 – это магнитная проницаемость вакуума, n – это число витков, а I – значение тока.
Когда ток движется по соленоиду, то катушка запасает энергию, которая равна работе, необходимая для установления тока. Чтобы вычислить в этом случае индуктивность, формула используется следующая:
где L показывает значение индуктивности, а E – запасающую энергию.
ЭДС самоиндукции возникает при изменении тока в соленоиде.
В случае работы на переменном токе появляется переменное магнитное поле. Направление силы притяжения может изменяться, а может оставаться неизменным. Первый случай возникает при использовании соленоида как электромагнита. А второй, когда якорь сделан из магнитомягкого материала. Соленоид на переменном токе имеет комплексное сопротивление, в которое включаются сопротивление обмотки и ее индуктивность.







Самое распространенное применение соленоидов первого типа (постоянного тока) — это в роли поступательного силового электропривода. Сила зависит от строения сердечника и корпуса. Примерами использования являются работа ножниц при отрезании чеков в кассовых аппаратах, клапаны в двигателях и гидравлических системах, язычки замков. Соленоиды второго типа применяются как индукторы для индукционного нагрева в тигельных печах.
Цепь переменного тока
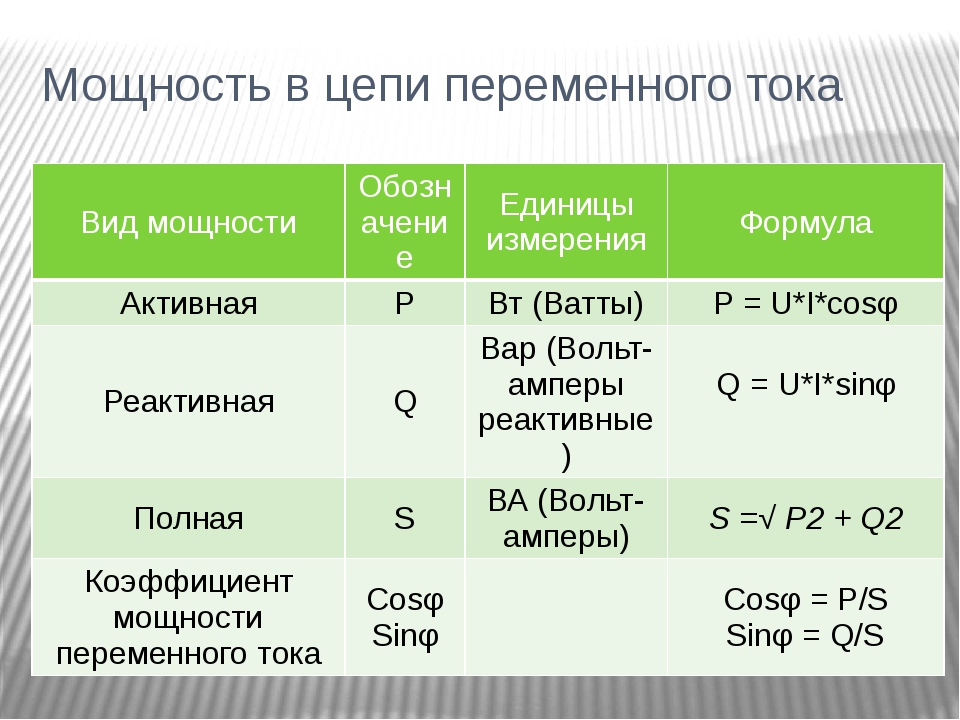
В цепи переменного сигнала напряжение и ток описываются с помощью следующих формул: U = Um*sin w*t и I = Im**sin w*, где: Um и Im — мгновенные значения величин (измеренные в определённое значение времени), а w — циклическая частота. Подставляя эти формулы в выражение для нахождения мощности, можно получить следующее: P = Um*Im *sin2w*t = U*I — U*I *cos2w*t, где U*I = Um*Im/2.
Подставив эти выражения в главную формулу можно получить следующее реактивное обозначение мощности Q = Um*Im*sinw*t*cosw*t = Um*Im*sin2w*t/2 = U*I *sin2w*t. Проанализировав это математическое определение, можно установить, что реактивная энергия состоит только из переменной части, которая изменяется с удвоенной частотой, при этом её среднее значение равно нулю.
В электротехнике существует такое понятие, как треугольник мощности. Представляет он собой прямоугольную геометрическую фигуру, катетами которой являются Q и P, а гипотенузой S. Угол между катетом и гипотенузой обозначается φ. Исходя из того, мощность равна:
Применив теорему Пифагора, получится формула для нахождения полной мощности S = (P 2 + Q 2)½.