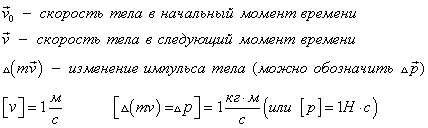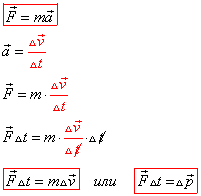в чем измеряется импульс силы в физике
Импульс тела. Импульс силы. Закон сохранения импульса
Все верно. Но оказывается, что с помощью импульса тела иногда удобнее описывать движение тела. Сейчас мы рассмотрим пример, из которого вам станет ясно, что такое импульс тела и чем он хорош.
Отличаются ли друг от друга два этих случая: движение велосипедиста и движение грузовика? Ведь они едут с одинаковой скоростью. Будут ли отличаться последствия, если велосипедист врежется в забор или грузовик врежется в забор? Да, конечно. В случае грузовика последствия будут более разрушительными для забора.
Что это значит? Что только скоростью характеризовать движение тела не очень удобно. Очень логично в свете приведенного примера с грузовиком и велосипедистом выглядит величина импульс тела :
Импульс тела — это векторная величина, равная произведению массы тела на скорость тела.
Ну ооочень логичное определение. Чем больше скорость и чем больше масса тела, тем более «разрушительные» последствия могут быть от действий этого тела. Это объяснение «на пальцах».
Хочется отметить, что импульс тела — это векторная величина. И импульс тела p ⃗ \vec
p ⃗ сонаправлен со скоростью тела V ⃗ \vec
Для импульса нет специальной единицы измерения (вакантное место — можете предложить свою фамилию в качестве кандидата на роль единицы измерения импульса). Импульс по-простому измеряется в к г ⋅ м с кг\cdot\frac<м> <с>к г ⋅ с м :
Количество движения
Количество движения как физическая величина впервые появилось в научных трудах ученых нового времени, в частности в XVII веке. Здесь важно отметить две фигуры: это Галилео Галилей, знаменитый итальянец, который обсуждаемую величину так и называл impeto (импульс), и Исаак Ньютон, великий англичанин, который помимо величины motus (движения) также использовал понятие vis motrix (движущая сила).
Вам будет интересно: Нужно ли высшее образование в наше время: личностное развитие, современные условия приема на работу, советы в построении карьеры
Итак, названные ученые под количеством движения понимали произведение массы объекта на скорость его линейного перемещения в пространстве. Это определение на языке математики записывается так:
Обратим внимание, что речь идет о величине векторной (p¯), направленной в сторону движения тела, которая пропорциональна модулю скорости, а роль коэффициента пропорциональности играет масса тела.
Связь импульса силы и изменения величины p¯
Вам будет интересно: Нужно ли высшее образование в наше время: личностное развитие, современные условия приема на работу, советы в построении карьеры
Как было сказано выше, помимо количества движения Ньютон ввел еще понятие движущей силы. Эту величину он определил так:
F¯ = m*dv¯/dt или F¯*dt = m*dv¯ =>
F¯*dt = dp¯, где dp¯ = m*dv¯
Анализ формулы
Из анализа формулы следует важный вывод: единицы измерения импульса силы совпадают с таковыми для p¯ (ньютон в секунду и килограмм на метр в секунду), более того, первая величина равна изменению второй, поэтому вместо импульса силы часто используют фразу «импульс тела», хотя более правильно говорить «изменение количества движения».
Силы, зависящие и не зависящие от времени
Выше закон импульса силы был представлен в дифференциальной форме. Чтобы посчитать значение этой величины, необходимо провести интегрирование по времени действия. Тогда получаем формулу:
Теперь рассмотрим более простую ситуацию, которая реализуется в ряде экспериментальных случаев: будем считать, что сила от времени не зависит, тогда можно легко взять интеграл и получить простую формулу:
F¯*∫t1t2 dt = Δp¯ => F¯*(t2-t1) = Δp¯
Последнее равенство позволяет рассчитать импульс постоянной силы.
При решении реальных задач на изменение количества движения, несмотря на то, что сила в общем случае зависит от времени действия, ее полагают постоянной и вычисляют некоторую эффективную среднюю величину F¯.
Примеры проявления на практике импульса силы
Какую роль играет эта величина, проще всего понять на конкретных примерах из практики. Перед тем как их привести, выпишем еще раз соответствующую формулу:
Теперь приведем конкретные примеры импульса силы в действии:
Понятие о моменте силы и его импульсе
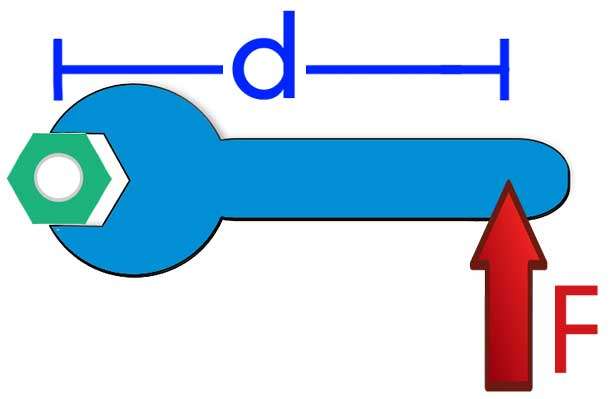
Момент силы отражает способность последней выполнить кручение системы вокруг оси. Например, если взяться за гаечный ключ подальше от гайки (большой рычаг d¯), то можно создать большой момент M¯, что позволит открутить гайку.
По аналогии с линейным случаем импульс M¯ можно получить, умножив его на промежуток времени, в течение которого он воздействует на вращающуюся систему, то есть:
Величина ΔL¯ носит название изменения углового момента, или момента импульса. Последнее уравнение имеет важное значение для рассмотрения систем с осью вращения, ведь оно показывает, что момент импульса системы будет сохраняться, если отсутствуют внешние силы, создающие момент M¯, что математически записывается так:
Если M¯= 0, тогда L¯ = const
Таким образом, оба уравнения импульсов (для линейного и кругового движения) оказываются аналогичными в плане их физического смысла и математических следствий.
Задача на столкновение птицы и самолета
Эта проблема не является чем-то фантастическим. Такие столкновения действительно происходят довольно часто. Так, по некоторым данным в 1972 году на территории воздушного пространства Израиля (зона наиболее плотной миграции птиц) было зарегистрировано около 2,5 тысяч столкновений птиц с боевыми и транспортными самолетами, а также с вертолетами.
Задача заключается в следующем: необходимо приблизительно рассчитать, какая сила удара приходится на птицу, если на пути ее движения встречается самолет, летящий со скоростью v=800 км/ч.
Перед тем как приступать к решению, примем, что длина птицы в полете составляет l = 0,5 метра, а ее масса равна m = 4 кг (это может быть, например, селезень или гусь).
Пренебрежем скоростью движения птицы (она мала в сравнении с таковой для самолета), а также будем считать массу самолета намного большей, чем птицы. Эти приближения позволяют говорить, что изменение количества движения птицы равно:
Для вычисления силы удара F необходимо знать продолжительность этого инцидента, она приблизительно равна:
Комбинируя эти две формулы, получаем искомое выражение:
Подставив в него цифры из условия задачи, получаем F = 395062 Н.
Более наглядно будет перевести эту цифру в эквивалентную массу, используя формулу для веса тела. Тогда получим: F = 395062/9,81 ≈ 40 тонн! Иными словами птица воспринимает столкновение с самолетом так, будто на нее свалилось 40 тонн груза.
Импульс силы — определение, формула и закон сохранения величины
С помощью законов Ньютона можно решать задачи, если известны все факторы, влияющие на физическое тело. Однако некоторые виды воздействия настолько кратковременны, что их трудно измерить. В этом случае вводят новые показатели — импульс силы и тела. Эти величины используются, чтобы не решать физических уравнений, а сразу перейти к их следствиям, что упрощает решение некоторых задач.
История открытия
Слово «импульс» в переводе с латинского означает «толчок». В некоторых книгах вместо этого термина используется термин «количество движения». Это понятие ввели в науку тогда же, когда Исаак Ньютон открыл и сформулировал законы, которые позже были названы в его честь.
Впервые слово «импульс» использовал учёный Рене Декарт в начале XVII века. Тогда в физике ещё не применялось понятие массы. Декарт определил эту математическую величину как произведение скорости тела и его «величины». В дальнейшем Ньютон уточнил формулировку Декарта. Согласно его определению, импульс (или количество движения) пропорционален величине скорости и массы движущегося тела.
Определение и свойства
Импульсом силы в физике принято называть величину, равную произведению этой силы на время. Фактически она представляет собой следующую закономерность F∆t = ∆P (формула импульса силы). Отсюда можно вычислить, в чём измеряется импульс силы — эти единицы называются ньютон-секундами. С помощью этого произведения можно описать следующие физические явления:
В релятивистской физике соотношение кинетической энергии и количества движения электрона характеризуется выражением p = (T 2 + 2Tmc 2 ) ½ /c.
Силы одинаковой величины, которые действуют на протяжении одинакового отрезка времени, вызывают одинаковые импульсы силы. Причём этот показатель не зависит от массы тела.
Для показателя изменения справедливо и обратное утверждение. Сумма сил, которые действуют на тело, равна отношению импульса силы ко времени.
В переводе с латинского слово «импульс» означает «толчок». Этот термин в некоторых источниках заменён на «количество движения».
Импульс силы направлен в ту же сторону, что и вектор скорости движения.
Импульс тела
Согласно современному определению, импульсом тела принято называть физическую величину, которая равняется произведению массы и скорости: P = mV, где P и V являются векторными величинами.
Направление вектора этого параметра сонаправлено с вектором скорости. Общепринятой единицей измерения в системе СИ принято считать 1 кг*м/с. Такие характеристики имеет тело массой в 1 кг, движущееся в пространстве со скоростью 1 м/с.
Этот показатель используется в физике для описания механического движения материальной точки. В быту люди оценивают движение тела через его скорость. Чем больше скорость, с которой перемещается тело в пространстве, тем больше его «количество движения». Если тело встречает на своём пути преграду, их взаимодействие зависит не только от скорости, но и от массы.
Например, по дороге с одинаковой скоростью движется мотоцикл и грузовик с кузовом, полным камня. При столкновении с забором или другой преградой разрушения от грузовика будут гораздо больше, чем от мотоцикла. Отсюда видно, что одной скорости недостаточно для характеристики движения, поэтому используется понятие «импульс тела».
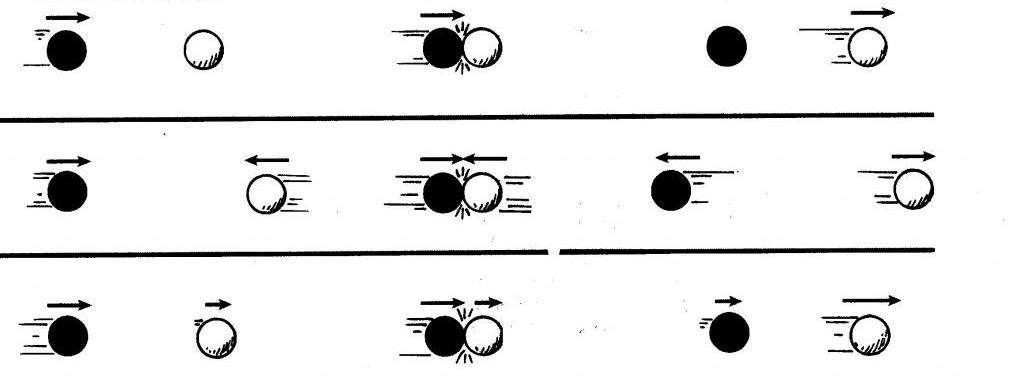
Взаимодействие в замкнутой системе
Если два физических тела взаимодействуют между собой, одно из них может частично или полностью передавать другому свой импульс. Если при этом на объекты не действуют дополнительные факторы, такую систему принято называть замкнутой.
При таких условиях векторная сумма импульсов всех объектов системы будет сохраняться. При этом она не зависит от характера и количества взаимодействий между участниками системы. Это правило получило название закона сохранения импульса, формула которого выглядит как p1 +p2 = p1′ +p2′. Оно выведено из второго и третьего законов Ньютона.
В качестве примера можно взять 2 произвольных взаимодействующих объекта, на которые не действуют никакие внешние факторы:
Таким образом, при парном взаимодействии тел в замкнутой системе внутренние силы не меняют векторную сумму всех импульсов, входящих в неё. С помощью этого правила можно находить скорости объектов в закрытой системе, даже если неизвестны показатели действующих сил. В качестве примера можно рассмотреть реактивное движение:
Если тело или частица сохраняет неподвижность, количество движения равняется нулю. Напротив, любая движущаяся точка обладает показателем, отличным от 0. Количество движения тела изменяется пропорционально его скорости.
Закон сохранения может оказаться справедливым и для незамкнутой системы. Это возможно, если сила или время внешнего воздействия стремится к нулю. В этом случае внешними показателями можно пренебречь.
Принцип решения задач
Приведённый закон часто используется для решения физических задач. Общая схема их решения выглядит следующим образом:
Выведение законов Ньютона
Известно, что импульс силы равняется изменению импульса тела:
Ft = mv—mv0, тогда Ft = m (v—v0). Отсюда следует, что F = m (v—v0)/t.
Отношение изменения скорости ко времени — это показатель ускорения. Таким образом, сила зависит от ускорения. Если записать уравнение как a = (v—v0)/t, можно вывести формулу второго закона: F = ma.
Можно сформулировать закон и по-другому: сила, которая была приложена к физическому объекту, равняется отношению изменения величины импульса к отрезку времени, за который он изменился.
Третий закон Ньютона выводится исходя из закона сохранения импульса. Для нахождения используются векторные показатели скоростей, то есть скорость может иметь различное направление.
Время в закрытой системе для двух взаимодействующих объектов является величиной одинаковой. Исходя из этого, формулировка третьего закона звучит следующим образом: два объекта взаимодействуют, при этом имеют одинаковую величину силы, но противоположные по направленности векторы, которые идут по направлению к друг другу. Отсюда следует, что модульные значения этих сил равнозначны.
Применение этих законов затруднительно при оценке кратковременного взаимодействия объектов (удара). В этом случае удобнее использовать для расчётов закономерности сохранения силы и количества движения.
I. Механика
Тестирование онлайн
Импульс тела
Пуля 22-го калибра имеет массу всего 2 г. Если кому-нибудь бросить такую пулю, то он легко сможет поймать ее даже без перчаток. Если же попытаться поймать такую пулю, вылетевшую из дула со скоростью 300 м/с, то даже перчатки тут не помогут.
Если на тебя катится игрушечная тележка, ты сможешь остановить ее носком ноги. Если на тебя катится грузовик, следует уносить ноги с его пути.
Импульс это векторная величина, которая определяется по формуле
Импульс служит мерой того, насколько велика должна быть сила, действующая в течение определенного времени, чтобы остановить или разогнать его с места до данной скорости.
Направление вектора импульса всегда совпадает с направлением вектора скорости.
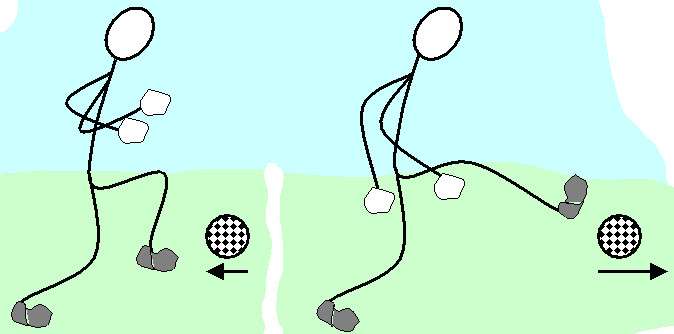
Если тело покоится, импульс равен нулю. Ненулевым импульсом обладает любое, движущееся тело. Например, когда мяч покоится, его импульс равен нулю. После удара он приобретает импульс. Импульс тела изменяется, так как изменяется скорость.
Импульс силы
Это векторная величина, которая определяется по формуле
Изменение импульса тела равно импульсу равнодействующей всех сил, действующих на тело. Это иная формулировка второго закона Ньютона
Рассмотрим задачу, которая демонстрирует связь импульса силы и изменения импульса тела.
Изменение импульса тела
Как определить изменение импульса тела? Необходимо найти численное значение импульса в один момент времени, затем импульс через промежуток времени. От второй найденной величины отнять первую. Внимание! Вычитать надо вектора, а не числа. То есть из второго вектора импульса отнять первый вектор. Смотрите вычитание векторов.
Пример. Оценить среднюю силу со стороны пола, действующую на мяч во время удара.
1) Во время удара на мяч действуют две силы: сила реакции опоры, сила тяжести.
Сила реакции изменяется в течение времени удара, поэтому возможно найти среднюю силу реакции пола.
2) Изменение импульса 
тела изображено на рисунке
3) Из второго закона Ньютона
Главное запомнить
1) Формулы импульса тела, импульса силы;
2) Направление вектора импульса;
3) Находить изменение импульса тела
Вывод второго закона Ньютона в общем виде
График F(t). Переменная сила
Импульс силы численно равен площади фигуры под графиком F(t).
Если же сила непостоянная во времени, например линейно увеличивается F=kt, то импульс этой силы равен площади треугольника. Можно заменить эту силу такой постоянной силой, которая изменит импульс тела на ту же величину за тот же промежуток времени
Импульс силы. Импульс тела
Конспект по физике для 8 класса «Импульс силы. Импульс тела». ВЫ УЗНАЕТЕ: Что такое импульс силы. Что такое импульс тела.
Импульс силы. Импульс тела
ИМПУЛЬС СИЛЫ
Вспомним формулу ускорения: 
Подставим в формулу второго закона Ньютона формулу ускорения. В результате получим 
ИМПУЛЬС ТЕЛА
Физическую величину, равную произведению массы тела на скорость его движения, называют импульсом тела или количеством движения тела. Импульс тела обозначается буквой p :
Если тело покоится, то его импульс равен нулю. Импульс тела — векторная величина. Направление вектора импульса совпадает с направлением вектора скорости тела. Под телом здесь понимается материальная точка.
ЕДИНИЦЫ ИМПУЛЬСА
Единицей импульса в СИ является килограмм-метр в секунду (1 кг•м/с)
ИМПУЛЬС ТЕЛА И ВТОРОЙ ЗАКОН НЬЮТОНА
И. Ньютон формулировал свой закон следующим образом: «Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует».
Действительно, из формулы (1) можно записать: 
Говоря «изменение количества движения», Ньютон имел в виду изменение импульса тела, поэтому второй закон Ньютона можно переформулировать следующим образом: изменение импульса в единицу времени равно действующей на тело силе.
При помощи этого закона можно выразить взаимосвязь между импульсом силы и изменением импульса тела:
Математическая формулировка второго закона Ньютона, строго говоря, справедлива в случае, когда приложенная к телу сила в течение времени её действия постоянна, т. е. не меняется ни по направлению, ни по величине.
Объясняя свой второй закон, И. Ньютон писал: «Если какая-нибудь сила производит некоторое количество движения, то двойная сила производит двойное, тройная — тройное, будут ли они приложены разом все вместе или же последовательно и постепенно. Это количество движения… всегда происходит по тому же направлению, как и производящая его сила». 
Импульс силы равен изменению импульса тела.
РЕШЕНИЕ ЗАДАЧИ
Запишем условие задачи и решим её.
Вы смотрели Конспект по физике для 8 класса «Импульс силы. Импульс тела».