в чем измеряется энергия гельмгольца

Энергия Гельмгольца

Энергия Гельмгольца

Термодинамические потенциалы
Статья является частью серии «Термодинамика».
Внутренняя энергия
Энтальпия
Свободная энергия Гельмгольца
Энергия Гиббса
Большой термодинамический потенциал (Ω)
Разделы термодинамики
Начала термодинамики
Уравнение состояния
Термодинамические величины
Термодинамические потенциалы
Термодинамические циклы
Фазовые переходы
править

Свобо́дная эне́ргия Гельмго́льца (или просто свобо́дная эне́ргия) — термодинамический потенциал, убыль которого в квазистатическом изотермическом процессе равна работе, совершённой системой над внешними телами.

Содержание

Определение

Свободная энергия Гельмгольца для системы с постоянным числом частиц определяется так:

Отсюда дифференциал свободной энергии равен:

Для системы с переменным числом частиц дифференциал свободной энергии Гельмгольца записывается так:

где μ — химический потенциал, а N — число частиц в системе. При этом свободная энергия Гельмгольца для равновесного состояния записывается как функция .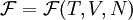

Свободная энергия Гельмгольца и устойчивость термодинамического равновесия

Можно показать, что в системе с фиксированными температурой и объемом положение устойчивого равновесия соответствует точке минимума свободной энергии Гельмгольца. Другими словами, в этой точке (для такой системы) никакие изменения макроскопических параметров невозможны.

Свободная энергия Гельмгольца и максимальная работа

Свободная энергия Гельмгольца получила своё название из-за того, что она является мерой работы, которую может совершить термодинамическая система над внешними телами.

Зададимся целью определить максимальную работу, которую система может совершить в этом случае.

Можно показать, что эта максимальная работа равна убыли свободной энергии Гельмгольца :

Свободные энергии Гельмгольца и Гиббса

В приложениях «свободной энергией» иногда называют не свободную энергию Гельмгольца, а энергию Гиббса. Это связано с тем, что энергия Гиббса также является мерой максимальной работы, но в данном случае рассматривается только работа над внешними телами, исключая среду:

См. также

Литература

Полезное

Смотреть что такое «Энергия Гельмгольца» в других словарях:

энергия Гельмгольца — Функция состояния термодинамической системы, равная разности между внутренней энергией и произведением термодинамической температуры на энтропию. Примечание Энергия Гельмгольца является характеристической функцией, если объем и термодинамическая… … Справочник технического переводчика

энергия Гельмгольца — энергия Гельмгольца; изохорно изотермический потенциал; отрасл. свободная энергия Функция состояния системы (А), определяемая разностью между внутренней энергией (U) и произведением термодинамической температуры (Т) на энтропию (S); A = U TS … Политехнический терминологический толковый словарь

энергия Гельмгольца — Helmholco energija statusas T sritis Standartizacija ir metrologija apibrėžtis Laisvoji energija arba izochorinis potencialas – termodinaminės sistemos parametras, kai sistemos tūris ir temperatūra nekinta. atitikmenys: angl. free energy;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

энергия Гельмгольца — Helmholco energija statusas T sritis chemija apibrėžtis Termodinaminės sistemos parametras, kai sistemos tūris ir temperatūra nekinta. atitikmenys: angl. free energy; Helmholtz energy; isochoric potential rus. изохорный потенциал; свободная… … Chemijos terminų aiškinamasis žodynas

энергия Гельмгольца — Смотри энергия Гельмгольца, изохорный потенциал … Энциклопедический словарь по металлургии

энергия Гельмгольца — Helmholco energija statusas T sritis fizika atitikmenys: angl. Helmholtz energy vok. Helmholtz Energie, f rus. энергия Гельмгольца, f pranc. énergie de Helmholtz, f … Fizikos terminų žodynas

энергия Гельмгольца — laisvoji Helmholco energija statusas T sritis fizika atitikmenys: angl. Helmholtz free energy vok. Helmholtzsche freie Energie, f rus. энергия Гельмгольца, f pranc. énergie libre de Helmholtz, f … Fizikos terminų žodynas

энергия Гельмгольца, изохорный потенциал — [Helmholtz free energy, thermodynamic potential] термодинамическая величина, функция состояния термодинамической системы, убыль которой в изохорно изотермическом процессе равна работе, производимой системой. Изменение величины энергии Гельмгольца … Энциклопедический словарь по металлургии

Свободная энергия Гельмгольца — У этого термина существуют и другие значения, см. Свободная энергия. Термодинамические потенциалы … Википедия

свободная энергия Гельмгольца — laisvoji Helmholco energija statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, išreiškiamas termodinaminės energijos U, termodinaminės temperatūros T ir entropijos S sandaugos skirtumu, t. y. A = U TS. atitikmenys: angl. Helmholtz … Penkiakalbis aiškinamasis metrologijos terminų žodynas

Источник

Энергия Гиббса. Энергия Гельмгольца. Направление процесса.

Чтобы дать ответ на вопрос о возможности протекания той или иной реакции, о ее направлении и глубине необходимо снова воспользоваться II – законом термодинамики, который может быть сформулирован следующим образом: любой самопроизвольно протекающий процесс, а также и химическая реакция, идет в том направлении, которое сопровождается уменьшением свободной энергии в системе (при постоянных температуре и давлении) или энергии Гельмгольца (при постоянных температуре и объеме).

Свободная энергия или Энергия Гиббса G – это та часть всей энергии системы, которую можно использовать для совершения максимальной работы.

Энергия Гельмгольца A — это та часть внутренней энергии системы, также определяющая работоспособность и может быть применена для совершения максимальной работы.

При протекании химических реакций единовременно совершаются два направления: стремление простых частиц объединиться в более сложные, а также стремление сложных частиц к распаду на более простые.

Они не зависят друг от друга и их величины противоположны, и процесс идет в сторону той реакции, при которой изменение величины больше. Разность между этими величинами определяет свободную энергию реакции (при постоянных температуре и давлении). Ее изменение в реакции определяется разностью сумм энергий Гиббса конечных продуктов реакции и исходных веществ:

При постоянных температуре и давлении изменение энергии Гиббса связано с энтальпией и энтропией следующим выражением:

Здесь изменение энергии Гиббса учитывает одновременно изменение энергетического запаса системы и степень ее беспорядка (самопроизвольность протекания процесса).

Т.к. энергия Гиббса является мерой самопроизвольности протекания процесса, то между знаком ΔG для любой реакции и ее самопроизвольным протеканием (при постоянных температуре и давлении) существуют такие зависимости:

Энтальпийный и энтропийный факторы и направление процесса

Выясним, как функция свободной энергии зависит от изменений энтропии и энтальпии идущего процесса. Вернемся к выражению, связывающему энергию Гиббса с энтальпией и энтропией:

Без энтропийных факторов все экзотермические реакции (ΔH˂0) должны были быть самопроизвольными. Но энтропийный фактор, который определяется величиной – TΔS, может привести к росту или, наоборот, к падению способности самопроизвольного протекания.

Так, при ΔS>0, член – TΔS вносит отрицательный вклад в общую величину ΔG, следовательно он повышает возможность реакции протекать самопроизвольно.

А при при ΔS 0Всегда ˂0Реакция самопроизвольна при любых температурах, обратная реакция всегда несамопроизвольна>0˂0Всегда >0Реакция несамопроизвольна при любых температурах, обратная реакция самопроизвольна˂0˂0При низких температурах ˂0, при высоких температурах >0Реакция самопроизвольна при низких температурах, обратная реакция становится самопроизвольной при высоких температурах>0>0При низких температурах >0, при высоких температурах ˂0Реакция несамопроизвольна при низких температурах, но при высоких температурах становится самопроизвольной

Величина ΔG 0 _р-ции позволяет определить, будет ли данная реакция, находящаяся в стандартных условиях, протекать самопроизвольно в прямом или обратном направлении. Аналогично теплоте образования, энергии Гиббса образования простых веществ равны нулю.

Энергия Гельмгольца системы с определенной внутренней энергией (U), энтропией (S) при абсолютной температуре (Т) определяется уравнением:

Изменение энергии Гельмгольца для процессов (при постоянных температуре и объеме) можно определить соотношением:

ΔA — величина, которая не зависит от пути, а зависит только от исходного и конечного состояния системы, т.е. ΔA также, как и другие рассмотренные термодинамические величины, является функцией состояния.

Энергия Гельмгольца подобно энергии Гиббса связана с самопроизвольностью протекания процесса. Если допустить, что система изолирована, а объем и температура постоянны, то самопроизвольно будут протекать только те процессы, при которых А уменьшается.

Таким образом, при ΔA 0 – в обратном направлении,

а при ΔA=0 система находится в состоянии равновесия.

Энергию Гельмгольца и энергию Гиббса в стандартных состояниях можно связать с константой равновесия:

Где R– универсальная газовая постоянная, K – константа равновесия, Т – абсолютная температура.

Если K>>1, т.е. реакция идет в прямом направлении, то ΔG 0 ˂˂0.

Если K 0 >>0

Если K=1, то ΔG 0 =0

В случае химической реакции, протекающей в гальваническом элементе при стандартных условиях ΔG 0 можно связать с ЭДС гальванического элемента следующим соотношением:

nF – количество прошедшего электричества

E 0 – электродвижущая сила, при условии что все вещества, принимающие участие в реакции, находятся в стандартном состоянии.

При самопроизвольном протекании процесса, его ΔG 0.

Порог реакционной способности веществ для большинства реакций имеет значение ΔG 0 ≈41 кДж/моль.

То есть, если ΔG 0 0 >+41 кДж/моль, то процесс неосуществим в любых реальных и стандартных условиях.

Источник

Свободная энергия Гельмгольца: единицы, как рассчитать, решаемые упражнения

Содержание:

В Свободная энергия Гельмгольца представляет собой термодинамический потенциал, который измеряет полезную работу замкнутой системы в условиях постоянной температуры и объема. Свободная энергия Гельмгольца обозначается какF y определяется как разность внутренней энергии ИЛИ минус произведение температуры Т по энтропии S:

Поскольку это энергия, она измеряется в Джоулях в Международной системе (СИ), хотя другие соответствующие единицы также могут быть эргами (СГС), калориями или электрон-вольтами (эВ).

Отрицательное изменение энергии Гельмгольца во время процесса приравнивается к максимальной работе, которую система может выполнять в изохорическом процессе, то есть при постоянном объеме. Когда уровень громкости не поддерживается постоянным, часть этой работы может выполняться с окружающей средой.

Если температура также постоянна, энергия Гельмгольца минимизируется при достижении равновесия. Для всего этого энергия Гельмгольца особенно полезна в процессах с постоянным объемом. В этом случае у вас есть:

— Для самопроизвольного процесса: ΔF 0.

Как рассчитывается свободная энергия Гельмгольца?

Как указано в начале, энергия Гельмгольца определяется как «внутренняя энергия U системы за вычетом произведения абсолютной температуры T системы на энтропию S системы»:

Это функция температуры T и объема V. Шаги, чтобы отобразить это, следующие:

— Исходя из первого закона термодинамики, внутренняя энергия U связана с энтропией S системы и ее объемом V для обратимых процессов следующей дифференциальной зависимостью:

Отсюда следует, что внутренняя энергия U является функцией переменных S Y V, Таким образом:

— Теперь возьмем определение F и получается:

— Подставляя туда дифференциальное выражение, полученное для dU на первом шаге, остается:

— Наконец, делается вывод, что F является функцией температуры T и объема V и может быть выражено как:

Спонтанные процессы

Энергию Гельмгольца можно применять как общий критерий спонтанности в изолированных системах, но сначала удобно уточнить некоторые понятия:

— Асистема закрыта он может обмениваться энергией с окружающей средой, но не может обмениваться материей.

— Вместо изолированная система он не обменивается веществом или энергией с окружающей средой.

— Наконец открытая система обмениваться веществом и энергией с окружающей средой.

В обратимых процессах изменение внутренней энергии рассчитывается следующим образом:

Теперь предположим процесс с постоянным объемом (изохорическим), в котором второй член предыдущего выражения не имеет никакого вклада. Также следует помнить, что согласно Неравенство Клаузиуса:

Такое неравенство относится к изолированной термодинамической системе.

Итак, для процесса (обратимого или нет), в котором объем остается постоянным, верно следующее:

T dS ≥ dU (при фиксированной громкости)

Принимая во внимание, что:

У нас будет, что в изохорном процессе при постоянной температуре выполняется следующее:dF ≤ 0, как указано в начале.

Таким образом, энергия Гельмгольца F является уменьшающейся величиной в спонтанном процессе, пока это изолированная система. F достигает минимального и стабильного значения при достижении обратимого равновесия.

Решенные упражнения

Упражнение 1

Вычислите изменение свободной энергии Гельмгольца F для 2 моль идеального газа при температуре 300K во время изотермического расширения, которое приводит к увеличению объема системы с начального 20 литров до конечного объема 40 литров.

Решение

Исходя из определения F:

Тогда конечная вариация F, называемая ΔF, будет:

Применяя это выражение:

ΔS = 2 моль x 8,314 Дж / (К моль) x ln (40 л / 20 л) = 11,53 Дж / K

Наконец, изменение энергии Гельмгольца:

Упражнение 2.

Внутри цилиндра находится поршень, который делит его на две части, и на каждой стороне поршня расположены п моль одноатомного идеального газа, как показано на рисунке ниже.

Стенки цилиндра хорошо проводят тепло (диатермический) и контактируют с резервуаром с температурой T_или.

а) Изменение внутренней энергии газа и работы, выполняемой системой и

б) Вариация энергии Гельмгольца.

Решение для

Поскольку поршень движется квазистатически, внешняя сила, приложенная к поршню, должна уравновешивать силу из-за разницы давлений в двух секциях цилиндра.

Работа dW в исполнении внешней силы F_доб во время бесконечно малого сдвига dx это:

Быть F₁ Y F₂ Энергии Гельмгольца в каждой из камер.

Конечная работа W может быть вычислена из конечного изменения энергии Гельмгольца каждой камеры:

Решение б

ΔS = nR ln (V_F/Увидел)

Это путем замены finally позволяет проделанной работе:

Быть ΔF_общее полное изменение энергии Гельмгольца.

Ссылки

Люди со СПИДом: это ваши особые потребности

Источник

СОДЕРЖАНИЕ

Определение

Энергия Гельмгольца определяется как

Формальное развитие

Первый закон термодинамики в замкнутой системе обеспечивает

Минимум бесплатной энергии и максимальные принципы работы

Законы термодинамики наиболее легко применимы к системам, в которых происходят обратимые процессы или процессы, которые начинаются и заканчиваются в тепловом равновесии, хотя необратимые квазистатические процессы или спонтанные процессы в системах с однородной температурой и давлением (u- PT- процессы) также могут быть проанализированы на основе фундаментальных термодинамическое соотношение, как показано ниже. Во-первых, если мы хотим описать такие явления, как химические реакции, может быть удобно рассмотреть подходящим образом выбранные начальное и конечное состояния, в которых система находится в (метастабильном) тепловом равновесии. Если система поддерживается в фиксированном объеме и находится в контакте с термостатом при некоторой постоянной температуре, то мы можем рассуждать следующим образом.

Δ U ванна + Δ U + W знак равно 0. <\ displaystyle \ Delta U _ <\ text <ванна>> + \ Delta U + W = 0.>

Объем системы остается постоянным. Это означает, что объем тепловой ванны также не изменяется, и мы можем сделать вывод, что тепловая баня не выполняет никакой работы. Это означает, что количество тепла, поступающего в тепловую ванну, определяется выражением

Тепловая баня остается в тепловом равновесии при температуре T независимо от того, что делает система. Следовательно, изменение энтропии термостата равно

Таким образом, полное изменение энтропии определяется выражением

Поскольку система находится в тепловом равновесии с термостатом в начальном и конечном состояниях, T также является температурой системы в этих состояниях. Тот факт, что температура системы не изменяется, позволяет нам выразить числитель как изменение свободной энергии системы:

Поскольку полное изменение энтропии всегда должно быть больше или равно нулю, получаем неравенство

Мы видим, что общий объем работы, которая может быть извлечена в изотермическом процессе, ограничивается уменьшением свободной энергии, и что увеличение свободной энергии в обратимом процессе требует выполнения работы в системе. Если работа не извлекается из системы, то

В случае наличия других внешних параметров указанное выше соотношение далее обобщается на

Связь с канонической статистической суммой

Z называется статистической суммой системы. Тот факт, что система не имеет уникальной энергии, означает, что различные термодинамические величины должны быть определены как математические ожидания. В термодинамическом пределе бесконечного размера системы относительные колебания этих средних значений будут равняться нулю.

Средняя внутренняя энергия системы является ожидаемым значением энергии и может быть выражена через Z следующим образом:

Среднее тепловое значение этого может быть записано как

Это означает, что изменение внутренней энергии определяется выражением

Отсюда следует, что энтропия системы определяется выражением

Связь свободной энергии с другими переменными

Объединяя определение свободной энергии Гельмгольца

наряду с фундаментальным термодинамическим соотношением

можно найти выражения для энтропии, давления и химического потенциала:

Эти три уравнения вместе со свободной энергией через статистическую сумму

позволяют эффективно вычислять интересующие термодинамические переменные с учетом статистической суммы и часто используются при расчетах плотности состояний. Можно также делать преобразования Лежандра для разных систем. Например, для системы с магнитным полем или потенциалом верно, что

Боголюбова неравенство

Неравенство Боголюбова часто формулируется несколько иначе, но равнозначно. Если мы запишем гамильтониан как

где точно разрешимо, то мы можем применить указанное выше неравенство, определив ЧАС 0 <\ displaystyle H_ <0>>

и, следовательно, неравенство

Доказательство

Для классической модели неравенство Боголюбова можно доказать следующим образом. Обозначим канонические распределения вероятностей для гамильтониана и пробного гамильтониана через и соответственно. Из неравенства Гиббса мы знаем, что: п р <\ displaystyle P_ > п

держит. Чтобы увидеть это, рассмотрите разницу между левой и правой сторонами. Мы можем записать это как:

это следует из того:

где на последнем шаге мы использовали, что оба распределения вероятностей нормированы на 1.

Мы можем записать неравенство в виде:

р ) ⟩ ≥ ⟨ бревно ⁡ ( п р ) ⟩ <\ displaystyle \ left \ langle \ log \ left (<\ tilde

> _ \ right) \ right \ rangle \ geq \ left \ langle \ log \ left (P_ \ right) \ right \ rangle \,>

Здесь мы использовали, что статистические суммы являются константами по отношению к усреднению, а свободная энергия пропорциональна минус логарифму статистической суммы.

⟨ ЧАС ⟩ знак равно ∑ р п

В правой части можно использовать неравенство

где мы ввели обозначение

для математического ожидания оператора Y в состоянии r. Смотрите здесь для доказательства. Логарифмирование этого неравенства дает:

Это позволяет нам писать:

Тот факт, что средние значения H и равны, приводит к тому же выводу, что и в классическом случае: ЧАС

Обобщенная энергия Гельмгольца

Приложение к фундаментальным уравнениям состояния

Приложение для обучения автокодировщиков

Хинтон и Земель «выводят целевую функцию для обучения автокодировщика на основе принципа минимальной длины описания (MDL)». «Длина описания входного вектора, использующего конкретный код, представляет собой сумму стоимости кода и стоимости восстановления. [Они] определяют это как энергию кода по причинам, которые станут ясны позже. Учитывая входной вектор, [ они] определяют энергию кода как сумму стоимости кода и стоимости восстановления «. Истинная ожидаемая совокупная стоимость составляет

«которая имеет в точности форму свободной энергии Гельмгольца».

Источник

Свободная энергия Гельмгольца

Термодинамические потенциалы
Статья является частью серии «Термодинамика».
Внутренняя энергия
Энтальпия
Свободная энергия Гельмгольца
Энергия Гиббса
Большой термодинамический потенциал (Ω)
Разделы термодинамики
Начала термодинамики
Уравнение состояния
Термодинамические величины
Термодинамические потенциалы
Термодинамические циклы
Фазовые переходы
править

Свобо́дная эне́ргия Гельмго́льца (или просто свобо́дная эне́ргия) — термодинамический потенциал, убыль которого в квазистатическом изотермическом процессе равна работе, совершённой системой над внешними телами.

Содержание

Определение

Свободная энергия Гельмгольца для системы с постоянным числом частиц определяется так:

Отсюда дифференциал свободной энергии равен:

Видно, что это выражение является полным дифференциалом относительно независимых переменных и . Поэтому часто свободную энергию Гельмгольца для равновесного состояния выражают как функцию .

Для системы с переменным числом частиц дифференциал свободной энергии Гельмгольца записывается так:

где — химический потенциал, а — число частиц в системе. При этом свободная энергия Гельмгольца для равновесного состояния записывается как функция .

Свободная энергия Гельмгольца и устойчивость термодинамического равновесия

Можно показать, что в системе с фиксированными температурой и объемом положение устойчивого равновесия соответствует точке минимума свободной энергии Гельмгольца. Другими словами, в этой точке (для такой системы) никакие изменения макроскопических параметров невозможны.

Свободная энергия Гельмгольца и максимальная работа

Свободная энергия Гельмгольца получила своё название из-за того, что она является мерой работы, которую может совершить термодинамическая система над внешними телами.

Пусть система переходит из состояния в состояние . Поскольку работа не является функцией состояния системы, работа, совершенная системой в данном процессе будет зависеть от пути, по которому этот переход будет осуществляться.

Зададимся целью определить максимальную работу, которую система может совершить в этом случае.

Можно показать, что эта максимальная работа равна убыли свободной энергии Гельмгольца :

Свободные энергии Гельмгольца и Гиббса

В приложениях «свободной энергией» иногда называют не свободную энергию Гельмгольца, а энергию Гиббса. Это связано с тем, что энергия Гиббса также является мерой максимальной работы, но в данном случае рассматривается только работа над внешними телами, исключая среду:

См. также

Литература

Выделить Свободная энергия Гельмгольца и найти в:

Источник