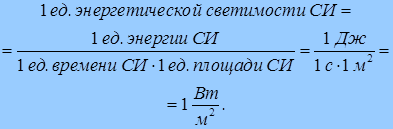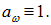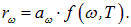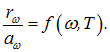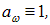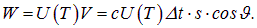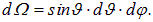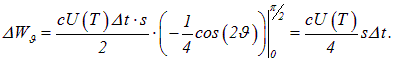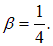в чем измеряется энергетическая светимость
В чем измеряется энергетическая светимость
§ 4 Энергетическая светимость. Закон Стефана-Больцмана.
Закон смещения Вина

[ R Э ] =Дж/(м 2 ·с) = Вт/м 2
Закон Й. Стефана (австрийский ученый) и Л. Больцмана (немецкий ученый)
Энергетическая светимость абсолютно черного тела пропорциональна четвертой степени термодинамической температуры.
Смещение Вина происходит потому, что с ростом температуры максимум излучательной способности смещается в сторону коротких длин волн.
§ 5 Формула Рэлея-Джинса, формула Вина и ультрафиолетовая катастрофа
Закон Стефана-Больцмана позволяет определять энергетическую светимость R Э а.ч.т. по его температуре. Закон смещения Вина связывает температуру тела с длиной волны, на которую приходятся максимальная лучеиспускательная способность. Но ни тот, ни другой закон не решают основной задачи о том, как велика лучеиспускательная, способность, приходящаяся на каждую λ в спектре а.ч.т. при температуре Т. Для этого надо установить функциональную зависимость r λ ,Т от λ и Т.
Основываясь на представлении о непрерывном характере испускания электромагнитных волн в законе равномерного распределения энергий по степеням свободы, были получены две формулы для лучеиспускательной способности а.ч.т.:
Опытная проверка показала, что для данной температуры формула Вина верна для коротких волн и даёт резкие расхождения с опытом в области длинных волн. Формула Рэлея-Джинса оказалась верна для длинных волн и не применима для коротких.

Если попытаться вычислить R Э с помощью формулы Рэлея-Джинса, то
§6 Квантовая гипотеза и формула Планка.
где
Так как излучение происходит порциями, то энергия осциллятора (колеблющегося атома, электрона) Е принимает лишь значения кратные целому числу элементарных порций энергии, то есть только дискретные значения
Впервые влияние света на ход электрических процессов было изучено Герцем в 1887 году. Он проводил опыты с электрическим разрядником и обнаружил, что при облучении ультрафиолетовым излучением разряд происходит при значительно меньшем напряжении.
В 1889-1895 гг. А.Г. Столетов изучал воздействие света на металлы, используя следующую схему. Два электрода: катод К из исследуемого металла и анод А (в схеме Столетова – металлическая сетка, пропускающая свет) в вакуумной трубке подключены к батарее так, что с помощью сопротивления R можно изменять значение и знак подаваемого на них напряжения. При облучении цинкового катода в цепи протекал ток, регистрируемый миллиамперметром. Облучая катод светом различных длин волн, Столетов установил следующие основные закономерности:
Ленард и Томсон в 1898 году измерили удельный заряд (е/ m ), вырываемых частиц, и оказалось, что он равняется удельному заряду электрона, следовательно, из катода вырываются электроны.
Внешним фотоэффектом называется испускание электронов веществом под действием света. Электроны, вылетающие из вещества при внешнем фотоэффекте, называются фотоэлектронами, а образуемый ими ток называется фототоком.
С помощью схемы Столетова была получена следующая зависимость фототока от 

Фе – световой поток (мощность излучения).
1-й закон внешнего фотоэффекта (закон Столетова):
При фиксированной частоте падающего света фототок насыщения пропорционален падающему световому потоку:
Ф, ν = const
следовательно, можно найти максимальную скорость вылетающих фотоэлектронов Vmax

2- й закон фотоэффекта : максимальная начальная скорость Vmax фотоэлектронов не зависит от интенсивности падающего света (от Ф), а определяется только его частотой ν
3- й закон фотоэффекта : для каждого вещества существует «красная граница» фотоэффекта, то есть минимальная частота νкp, зависящая от химической природы вещества и состояния его поверхности, при которой ещё возможен внешний фотоэффект.
Так как по волновой теории энергия, передаваемая электромагнитным полем пропорциональна интенсивности света (Ф), то свет любой; частоты, но достаточно большой интенсивности должен был бы вырывать электроны из металла, то есть красной границы фотоэффекта не существовало бы, что противоречит 3-му закону фотоэффекта. Внешний фотоэффект является безынерционным. А волновая теория не может объяснить его безынерционность.
§ 3 Уравнение Эйнштейна для внешнего фотоэффекта.
Работа выхода
Уравнение Эйнштейна (закон сохранения энергии для внешнего фотоэффекта):
Энергия падающего фотона hv расходуется на вырывание электрона из металла, то есть на работу выхода Авых, и на сообщение вылетевшему фотоэлектрону кинетической энергии 
Наименьшая энергия, которую необходимо сообщить электрону для того, чтобы удалить его из твердого тела в вакуум называется работой выхода.
Уравнение Эйнштейна позволяет объяснить в c е три закона внешнего фотоэффекта,
1-й закон: каждый квант поглощается только одним электроном. Поэтому число вырванных фотоэлектронов должно быть пропорционально интенсивности (Ф) света
ν и т.к. Авых не зависит от Ф, то и Vmax не зависит от Ф
3-й закон: При уменьшении ν уменьшается Vmax и при ν = ν0 Vmax = 0, следовательно, hν 0 = Авых, следовательно, 
1.1. Тепловое излучение
Тепловое излучение — это электромагнитное излучение, испускаемое веществом за счет запасов его внутренней (тепловой) энергии.
Поэтому характеристики теплового излучения (интенсивность, спектральный состав) зависят от температуры излучающего вещества. Все прочие виды электромагнитного излучения существуют за счет других, не тепловых, форм энергии. Тепловое излучение — единственный вид излучения, которое может находиться в термодинамическом равновесии с веществом и само быть при этом в состоянии термодинамического равновесия. Ниже будет рассматриваться главным образом термодинамически равновесное тепловое излучение.
Предположим, что нагретое тело помещено в полость, стенки которой поддерживаются при некоторой постоянной температуре 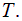
Рис. 1.1. Нагретое тело в полости с идеально отражающими стенками
Представим теперь то же самое тело, помещенное внутри другой оболочки, отличающейся размерами, формой или материалом, из которого она сделана. Будем поддерживать ту же самую температуру оболочки. В системе пойдут аналогичные процессы установления равновесия, в результате которых тело внутри оболочки нагреется до той же самой температуры Т. Для тела внутри оболочки ничего не изменилось: оно находится при той же самой температуре, что и прежде, и, следовательно, будет излучать ту же самую энергию. Так как тело находится в равновесии с излучением внутри оболочки, мы приходим к выводу, что характеристики этого излучения не зависят от свойств оболочки, но лишь от ее температуры. Это «стандартное», термодинамически равновесное излучение называется излучением абсолютно черного тела. О том, откуда такое название и что такое абсолютно черное тело будет сказано ниже. Равновесное излучение можно охарактеризовать плотностью энергии 
Плотность энергии 
Тепловое излучение состоит из электромагнитных волн разных частот. Полная плотность энергии складывается из плотностей энергий этих волн. Для более детальной характеристики излучения вводят дифференциальную величину — спектральную плотность энергии излучения 
Спектральная плотность энергии излучения — это энергия излучения в единице объема, приходящаяся на единичный интервал частот.
Иными словами, если обозначить через 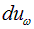

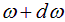
В системе СИ спектральная плотность энергии измеряется в следующих единицах:
Плотность энергии 
Итак, в полости, существует стандартное излучение с плотностью энергии 
Энергетическая светимость R (интегральная плотность потока энергии излучения) — равна энергии, испускаемой в единицу времени единицей поверхности излучающего тела по всем направлениям.
В системе СИ энергетическая светимость измеряется в 
Энергетическая светимость зависит от температуры тела. Тепловое излучение состоит из волн различных частот. Для характеристики теплового излучения важно знать, какая энергия, в каком диапазоне частот излучается телом. Поэтому вводят дифференциальную характеристику 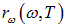
Испускательная способность тела (спектральная плотность потока энергии излучения) — это количество энергии, испускаемой в единицу времени единицей поверхности тела в единичном интервале частот по всем направлениям.
Чтобы получить энергетическую светимость тела, надо проинтегрировать испускательную способность по всем частотам:
В системе СИ испускательная способность тела (спектральная плотность потока энергии излучения) измеряется в Дж/м 2 :
Нагретое тело не только испускает энергию, но и поглощает ее. Для описания способности тела поглощать энергию падающего на его поверхность излучения вводится величина, которая так и называется: поглощательная способность.
Поглощательная способность 
Поглощательная способность равна той доли, которую — в заданном спектральном интервале 


Очевидно, что поглощательная способность тела является безразмерной величиной, не превышающей единицу.
Абсолютно черное тело — это тело, способное поглощать при любой температуре все падающее на него излучение всех частот.
Для абсолютно черного тела
Тел с такими свойствами в природе не бывает, это очередная физическая идеализация.
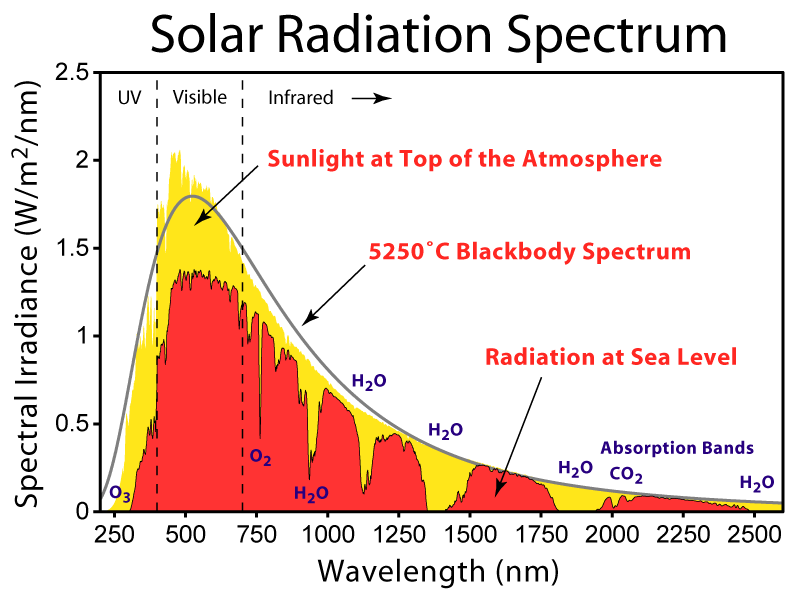
Рис. 1.2. Спектр излучения абсолютно чёрного тела (чёрная линия) при температуре 5250 °С хорошо моделирует излучение Солнца. Красным цветом показаны результаты измерений на уровне моря, жёлтым — в верхней атмосфере.
Будем поочередно помещать в полость различные тела. Все они находятся в одинаковых условиях, в окружении одного и того же излучения. Обозначим 
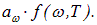
Различные тела в полости имеют разную поглощательную способность, следовательно, у них будет и разная испускательная способность, так что отношение rw /аw не зависит от конкретного тела, помещенного в полость:
С другой стороны, испускательная способность тела не зависит от полости, в которую оно помещено, но лишь от свойств тела. Таким образом, функция 
Отношение испускательной и поглощательной способности тела не зависит от природы тела. Для всех тел функция 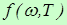
Строго говоря, сформулированное выше утверждение справедливо в условиях термодинамического равновесия, наличие которого здесь и ниже всегда предполагается.
Для абсолютно черного тела
откуда следует физическая интерпретация универсальной функции Кирхгофа 
(Характеристики абсолютно черного тела будем помечать звездочкой, а само тело называть нередко просто «черным», а не абсолютно черным).
Рис. 1.3. Густав Роберт Кирхгоф (1824–1887)
Установим теперь связь между испускательной способностью черного тела 


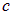
Найдем безразмерный коэффициент пропорциональности 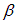
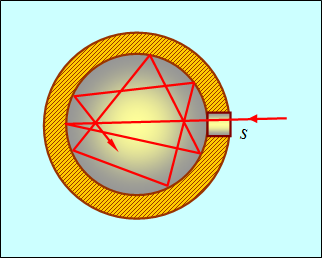
Рис. 1.4. Полocть с небольшим отверстием — реализация черного тела
Луч света, падающий внутрь этой полости через отверстие s, претерпевает многократное отражение. При каждом отражении стенки полости поглощают часть энергии. Поэтому интенсивность луча света, выходящего из отверстия, во много раз меньше интенсивности входящего луча. Чем больше отношение площади полости к площади отверстия, тем ближе такое тело к абсолютно черному. Поэтому отверстие в полости излучает как абстрактное черное тело.
Рис. 1.5. Тепловое излучение из отверстия в полости
Объем такого цилиндра равен
Содержащаяся в нем энергия теплового излучения равна
Но не вся она распространяется под углом 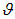
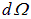

Так как полный телесный угол равен 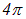
Теперь осталось проинтегрировать 
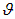
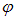

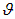

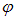

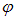

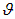
Разделив 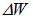
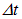
Итак, энергетическая светимость черного тела 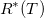

Аналогичное соотношение справедливо для спектральных характеристик излучения черного тела: