в чем измеряется децибел
Децибел
Децибе́л — логарифмическая единица уровней, затуханий и усилений. [1]
Величина, выраженная в децибелах, численно равна десятичному логарифму безразмерного отношения физической величины к одноимённой физической величине, принимаемой за исходную, умноженному на десять:
где AdB — величина в децибелах, A — измеренная физическая величина, A0 — величина, принятая за базис.
Децибел — это безразмерная единица, применяемая для измерения отношения некоторых величин — «энергетических» (мощности, энергии, плотности потока мощности и т. п.) или «силовых» (силы тока, напряжения и т. п.). Иными словами, децибел — это относительная величина. Не абсолютная, как, например, ватт или вольт, а такая же относительная, как кратность («трёхкратное отличие») или проценты, предназначенная для измерения отношения («соотношения уровней») двух других величин, причём к полученному отношению применяется логарифмический масштаб.
Русское обозначение единицы «децибел» — «дБ», международное — «dB» [2] (неправильно: дб, Дб).
Децибел не является официальной единицей в системе единиц СИ, хотя по решению Генеральной конференции по мерам и весам допускается его применение без ограничений совместно с СИ, а Международное бюро мер и весов рекомендовала включить его в эту систему.
Содержание
Сравнение с другими логарифмическими единицами
| название | сокращение | соответствует изменению в … раз | пересчёт в … | |||
|---|---|---|---|---|---|---|
| дБ | Б | Нп | X m | |||
| децибел | дБ, dB | ≈1,26 ( ) ) | 1 | 0,1 | ≈0,115 | −0,25 |
| бел | Б, B | 10 | 10 | 1 | ≈1,15 | −2,5 |
| непер | Нп, Np | ≈2,72 (e) | ≈8,686 | ≈0,8686 | 1 | ≈−1,086 |
| звёздная величина | X m | ≈0,398 ( ) ) | −4 | −0,4 | ≈−0,921 | 1 |
Области применения
Децибелы широко применяются в любых областях техники, где требуется измерение величин, меняющихся в широком диапазоне: в радиотехнике, антенной технике, в системах передачи информации, в оптике, акустике (в децибелах измеряется уровень громкости звука) и др. Так, в децибелах принято измерять динамический диапазон (например, диапазон громкости звучания музыкального инструмента), затухание волны при распространении в поглощающей среде, коэффициент усиления и коэффициент шума усилителя.
Децибелы используются не только для измерения отношения физических величин второго порядка (энергетических: мощность, энергия) и первого порядка (напряжение, сила тока). В децибелах можно измерять отношения любых физических величин, а также использовать децибелы для представления абсолютных величин (см. опорный уровень).
Переход к децибелам
Любые операции с децибелами упрощаются, если руководствоваться правилом: величина в дБ — это 10 десятичных логарифмов отношения двух одноименных энергетических величин. Всё остальное — следствия этого правила. «Энергетические» — величины второго порядка (энергия, мощность). По отношению к ним напряжение и сила электрического тока («неэнергетические») — величины первого порядка (P
U²), которые должны быть на каком-то этапе вычислений корректно преобразованы в энергетические. [источник не указан 153 дня]
Измерение «энергетических» величин
Изначально дБ использовался для оценки отношения мощностей, и в каноническом, привычном смысле величина, выраженная в дБ, предполагает логарифм отношения двух мощностей и вычисляется по формуле:

Соответственно, переход от дБ к отношению мощностей осуществляется по формуле:


Измерение «неэнергетических» величин
Из правила (см. выше) следует, что «неэнергетические» величины должны быть преобразованы в энергетические. Так, согласно закону Джоуля-Ленца 


В общем случае напряжения U1 и U0 могут регистрироваться на различных по величине сопротивлениях (R1 не равно R0). Такое может быть, например, при определении коэффициента усиления усилителя, имеющего различные выходное и входное сопротивления, или при измерении потерь в согласующем устройстве, трансформирующем сопротивления. Поэтому в общем случае
величина в децибелах = 
Только в частном (весьма распространенном) случае, если оба напряжения U1 и U0 измерялись на одном и том же сопротивлении (R1 = R0), можно пользоваться кратким выражением
величина в децибелах = 
Децибелы «по мощности», «по напряжению» и «по току»
Из правила (см. выше) следует, что дБ бывают только «по мощности». Тем не менее, в случае равенства R1 = R0 (в частности, если R1 и R0 — одно и то же сопротивление, или в случае, если соотношение сопротивлений R1 и R0 по той или иной причине не важно) говорят о дБ «по напряжению» и «по току», подразумевая при этом выражения:
дБ по напряжению = 

Для перехода от «дБ по напряжению» («дБ по току») к «дБ по мощности» следует чётко определить, на каких именно сопротивлениях (равных или не равных друг другу) регистрировались напряжение (ток). Если R1 не равно R0, следует пользоваться выражением для общего случая (см. выше).
Нетрудно подсчитать, что, в частности:
Примеры вычислений
Переход к дБ
Пусть значение мощности P1 стало в 2 раза больше исходного значения мощности P0, тогда
10 lg(P1/P0) = 10 lg(2) ≈3,0103 дБ ≈ 3 дБ,
то есть рост мощности на 3 дБ означает её увеличение в 2 раза.
Пусть значение мощности P1 стало в 2 раза меньше исходного значения мощности P0, то есть P1 = 0,5 P0. Тогда
то есть снижение мощности на 3 дБ означает её снижение в 2 раза. По аналогии:
Переход от дБ к «разам»
Изменение «в разах» по известному изменению в дБ (условное обозначение «dB» в формулах ниже) вычисляется следующим образом:
Переход от дБ к мощности
Для этого нужно знать значение опорного уровня мощности P0. Например, при P0 = 1 мВт и известном изменении на +20 дБ:

Переход от дБ к напряжению (току)
Для этого нужно знать значение опорного уровня напряжения U0 и определиться, регистрировалось ли напряжение на одинаковом сопротивлении, или же для решаемой задачи различие значений сопротивлений не важно. Например, при условии R0 = R1, заданном U0 = 2 В и приросте напряжения на 6 дБ:

Рекомендации
Операции с децибелами можно выполнять в уме: вместо умножения, деления, возведения в степень и извлечения корня применяется сложение и вычитание децибельных единиц. Для этого можно использовать таблицы соотношений (первые 2 — приближённые):
1 дБ → в 1,25 раза, 3 дБ → в 2 раза, 10 дБ → в 10 раз.
Отсюда, раскладывая «более сложные значения» на «составные», получаем:
6 дБ = 3 дБ + 3 дБ → в 2·2 = в 4 раза, 9 дБ = 3 дБ + 3 дБ + 3 дБ → в 2·2·2 = в 8 раз, 12 дБ = 4 · (3 дБ) → в 2 4 = в 16 раз
13 дБ = 10 дБ + 3 дБ → в 10·2 = в 20 раз, 20 дБ = 10 дБ + 10 дБ → в 10·10 = в 100 раз, 30 дБ = 3 · (10 дБ) → в 10³ = в 1000 раз
Сложению (вычитанию) значений в дБ соответствует умножение (деление) самих отношений. Отрицательные значения дБ соответствуют обратным отношениям. Например:
Причины использования децибелов
Для применения децибелов и оперирования логарифмами вместо процентов или долей есть ряд причин:
Условные обозначения
Для различных физических величин одному и тому же числовому значению, выраженному в децибелах, могут соответствовать разные уровни сигналов (вернее разности уровней). Поэтому во избежание путаницы такие «конкретизированные» единицы измерения обозначают теми же буквами «дБ», но с добавлением индекса — общепринятого обозначения измеряемой физической величины. Например дБВ (децибел относительно вольта) или дБмкВ (децибел относительно микровольта), дБВт (децибел относительно ватта) и т. п. В соответствии с международным стандартом МЭК 27-3 при необходимости указать исходную величину её значение помещают в скобках за обозначением логарифмической величины, например, для уровня звукового давления: LP (re 20 µPA) = 20 dB; LP (исх. 20 мкПа) = 20 дБ
Опорный уровень
Децибел служит для определения отношения двух величин. Но нет ничего удивительного в том, что децибел используют и для измерения абсолютных значений. Для этого достаточно условиться, какой уровень измеряемой физической величины будет принят за опорный уровень (условный 0 дБ).
Строго говоря, должно быть однозначно определено, какая именно физическая величина и какое именно её значение используются в качестве опорного уровня. Опорный уровень указывается в виде добавки, следующей за символами «дБ» (например, дБм), либо опорный уровень должен быть ясен из контекста (например, «дБ относительно 1 мВт»).
На практике распространены следующие опорные уровни и специальные обозначения для них:
По аналогии образуются составные единицы измерений. Например, уровень спектральной плотности мощности дБВт/Гц — «децибельный» аналог единицы измерения Вт/Гц (мощность, выделяющаяся на номинальной нагрузке в полосе частот шириной в 1 Гц с центром на указанной частоте). Опорным уровнем в данном примере является 1 Вт/Гц, то есть физическая величина «спектральная плотность мощности», её размерность «Вт/Гц» и значение «1». Так, запись «-120 дБВт/Гц» полностью эквивалентна записи «10 −12 Вт/Гц».
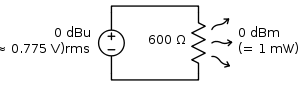
В случае затруднения во избежание путаницы достаточно указать опорный уровень явно. Например, запись −20 дБ (относительно 0,775 B на нагрузке 50 Ом) исключает двойное толкование.
Справедливы следующие правила (следствие правил действий с размерными величинами):
При пересчёте уровней мощностей (дБВт, дБм) в уровни напряжений (дБВ, дБмкВ) и обратно необходимо учитывать сопротивление, на котором определяется мощность и напряжение:
Что измеряется в децибелах, перевод в децибелы, децибел в разы, вольты, ватты и т.д.
Мы часто встречаем уровни звука, указанные в децибелах — дБ или dBu и привыкли считать что это единица измерения шума, звука. А вот и нет. Это совсем не так. Децибел — это не единица измерения вообще. Это относительная характеристика, которая может отражать напряжение, мощность, силу тока и т.д. Что-то типа процентов, долей, но в логарифмической зависимости. Сначала понять, что такое децибел, непросто, но затем оказывается, что это очень удобно.
Понятие децибела
Мы хорошо воспринимаем измерение каких-либо параметров в прямых величинах. Например, напряжение измеряется в вольтах, сила тока — в амперах, сопротивление — в омах и т.д. Когда говорим об этом, все ясно и понятно. Когда говорим об увеличении или снижении в этих прямых единицах измерения тоже все понятно. Например, напряжение с 220 вольт снизилось до 150 вольт. Все понятно. Выражение «мощность возросла на 50 ватт» тоже вопросов не вызывает.
Как понять что такое децибел и что он означает
Но иногда говорят об увеличении или уменьшении того же напряжения или мощности на 2 децибела. Как это понять? Что измеряется в децибелах? Ведь мощность меряем в ваттах? Как соотнести децибелы с ваттами или вольтами, амперами и другими величинами. Ведь так описывают многие параметры. Тут надо разбираться. Не очень просто сначала понять, но потом все становится очевидным.
Что значит бел и децибел
Сразу стоит уяснить, что бел и децибел — это не единицы измерения чего-либо. Это не результат измерений. Децибел — это величина, которая показывает насколько/во сколько раз изменился тот или иной параметр. То есть бел или децибел — это относительная величина, которая высчитывается при сравнении двух измерений одного и того же параметра.
Например, на рисунке дан график, который построили по результатам измерения напряжение на выходе прибора при изменении подаваемой на вход частоты (АЧХ). Сняты были характеристики при уровне сигнала 1 V (график 1) и 100 мV (график 2). Если смотреть на графики прямых измерений, понять что-то сложно. На втором рисунке график построен в децибелах. На этом графике очевидно, что реакция прибора одинаковая, изменился только уровень сигнала на выходе, что и понятно.
Два графика измерений. Левый — прямая зависимость (напряжения от частоты), правый — изменение напряжения в дБ при изменении частоты
Первоначально стали использовать единицу Бел. Международное обозначение бела — B, российское — Б (например, 10Б или 10B). Но более удобным оказалось применение одной ее десятой доли — децибела или дБ в российском обозначении и dBu в международном. То есть один децибел — это 0,1 Бела.
Дальше, к сожалению, без математики не обойтись. Придется вспомнить что такое десятичный логарифм. Десятичный логарифм показывает, в какую степень надо возвести число 10 чтобы получить требуемую цифру. На рисунке вы видите соотношение, возможно будет понятнее в таком виде.
Несколько значений десятичных логарифмов
Теперь, собственно о Белах и децибелах. Если говорить об определениях, то Бел — это десятичный логарифм отношения двух величин. Любых двух величин. Мощностей, напряжения, силы звука, частоты и т.д. Давайте на примере. Надо понять, что выдает прибор на выходе при изменении параметров на входе. Выбирают какую-то точку отсчета — базу. Затем изменяют параметр, проводят измерение результата, делят его на «базу» и берут десятичный логарифм. Получают результат измерения в децибелах. Так измеряют параметры, пересчитывают в децибелы и строят зависимости.
Формула, которая поясняет что такое дБ (децибел) и как их считают
На рисунке даны две формулы — для вычисления энергетических величин (по мощности) и амплитудных (по напряжению). Как видите, они отличаются только коэффициентом. U1 тут — это результат измерений, а Uo — базовая величина, с который сравнивают измерений.
Почему используют децибелы, а не прямые величины
Использование логарифмических зависимостей часто более понятно и несет больше информации, чем прямые измерения. Это видно на примере построения графиков амплитудно-частотной характеристики. И такой случай не единичный, многие зависимости более информативны в логарифмической зависимости.
Кроме того, децибелы используют в тех областях, где параметры изменяются в очень широком диапазоне. Более понятна нам ситуация со звуками. Человек в состоянии воспринимать частоты от 20 Гц до 20 000 Гц. Ничего себе разброс! В тысячу раз.
Интенсивность звука и его соответствие в дБА
Заметили разницу? Показатель увеличился в 100 раз, а в белах увеличился на 2 Б. Это удобнее. Согласитесь, проще оперировать единицами, чем сотнями тысяч. Важно просто понимать смысл сказанного. При возрастании прямых величин их надо умножать на то число, на которое параметр увеличился. При оперировании децибелами их складывают. Согласитесь, это проще.
Что такое dBm, dBv, dBA (дБм, дБв, дБА)
Как вы уже поняли, децибел — это относительная величина и отражать она может что угодно. Надо только выбрать точку отсчета, базу, эталон, с которым сравнивают все последующие изменения. База для сравнения может быть взята произвольно. Но тогда непонятно как соотносить разные измерения. В таком случае, обычно, указывают относительно чего считался логарифм. То есть, что подставляли в знаменатель (в формуле выше это Uo).
Для электротехники и мощностей были выбраны базовые точки отсчета — две величины напряжения, с которыми сравнивают большую часть измерений электрических величин.
На что влияет точка отсчета? Просто на уровень, на котором строится зависимость. Если же по данным построить график, он будет иметь ту же форму.
Как считают децибелы
Больше в ходу не Белы, а их десятая часть — децибелы (обозначение dB или дБ). Ведь чаще увеличение не в сотни и тысячи раз, а чуть поскромнее. Так что обычно говорят об увеличении того или иного показания или характеристики на 5 дБ или на 10 дБ.
Пример соответствия децибел и «раз»
Но важно помнить, что описанная выше прямая зависимость характерна только для энергетических величин (это если мощность возросла в 10 раз, то она увеличилась на 10 дБ). Для других зависимость тоже логарифмическая, но вычисляется по другой формуле. И это надо помнить.
| Децибелы | Соотношение мощностей | Соотношение амплитуд |
|---|---|---|
| -3 | 0,5 | 0,7 |
| -6 | 0,25 | 0,5 |
| -10 | 0,1 | 0,3 |
| -20 | 1,01 | 0,1 |
| -25 | 0,03 | 0,05 |
| -40 | 0,01 | 0,0001 |
| -60 | 0,001 | 0,000001 |
Возможно, поможет понять что такое децибел следующие сравнение. Представим, что мощность изменяется литрами. Соотношение между 0,5 литра и 1 литром такое же как и между 1 литром и 2 литрами. Это 0,5 и равно оно 6 дБ. Но если сравнивать 0,5 и 0,75 литра, то они относятся как 0,66(6) что в децибелах около 3,6 дБ. Примерно так.
Децибелы в акустике
Вы, возможно, удивитесь, но для акустики децибелы подходят просто идеально. Собственно, Александр Белл ввел понятие Бел при исследовании порога слышимости. Он определил, что «громкость» мы воспринимаем не по реальной мощности сигнала, а по десятичному логарифму от этой мощности. Как так? Давайте рассмотрим пример.
Имеется усилитель, который выдает сигнал мощностью 1 Вт. Чтобы увеличить его в 1,1 раза, добавить надо только 0,1 Вт. А если на выходе у нас 100 Вт, то чтобы увеличить мощность в 1,1 раза надо поднять мощность на 10 Вт. Увеличение громкости в обоих случаях будет «для уха» одинаковым, а увеличение мощности имеет явно нелинейный характер.
Мы воспринимаем не реальный уровень сигнала, а логарифмическую зависимость
На основании вот этого явления Белл и вывел то самое логарифмическое отношение. В его честь и названа эта относительная единица измерений. Что еще это нам дает? А вот такие факты:
Принять децибелы не так легко. Но наверное, вы уже поняли, что в децибелах громкость звука/шума не измеряется. Эта цифра показывает насколько изменился сигнал относительно «нулевой» точки восприятия. Примерно так можно это сформулировать.
Таблица уровней шумов
Ну, а чтобы было понятнее, приведем таблицу сравнений привычных, знакомых звуков и их среднего уровня.
| дБ | С чем можно сравнить | дБ | С чем можно сравнить |
|---|---|---|---|
| 0 дБ | Полная тишина | 90 дБ | Звук работающего фена, мотоцикла, поезда |
| 1 дБ | Самый нижний порог слышимости | 100-105 дБ | Ремонт и рок-концерт |
| 10-24 дБ | Шелест листвы | 110 дБ | Музыка в ночном клубе |
| 20 дБ | Шепот | 120 дБ | Автомобильный гудок |
| 40 дБ | Так звучит дождь | 130-135 дБ | Звук работающей дрели |
| 45 дБ | Тихий разговор | 140 дБ | Шум турбин самолета |
| 60 дБ | Громкий разговор | 160 дБ | Звук выстрела возле уха |
| 80-90 дБ | Шоссе с интенсивным движением | 200 дБ | Смертельный уровень шума |
Каждый шум или звук имеет определенный уровень мощности, но проще его описывать в децибелах
Факты, которые позволят оценить важность акустики и децибелов:
Вообще, постоянное нахождение в шумном помещении сильно снижает способность воспринимать звуки. Мало того, оно приводит к расстройствам психики, сна, что негативно сказывается и на общем самочувствии. Поэтому шумные производства — зона риска. Чтобы хорошо себя чувствовать, просто необходимо время от времени находится если не при полной тишине, то при низком уровне шума.
Перевод децибелов в разы
Давайте попробуем сформулировать что такое децибел по-другому. Децибел — это логарифм соотношения двух величин. Эта относительная величина, которая показывает во сколько одно значение больше или меньше другого (базового). «Во сколько раз» это нам понятно. Поэтому часто приходится переводить децибелы в разы и наоборот. Можно, конечно, посчитать, но проще пользоваться таблицей.
| дБ | Увеличение напряжения (силы тока) в разы | Увеличение мощности (энергетической составляющей) в разы | дБ | Увеличение напряжения (силы тока) в разы | Увеличение мощности (энергетической составляющей) в разы |
|---|---|---|---|---|---|
| 0 | 1 | 1 | 28 | 25,12 | 631 |
| 1 | 1,12 | 1,26 | 29 | 28,17 | 794 |
| 2 | 1,26 | 1,59 | 30 | 31,64 | 1000 |
| 3 | 1,41 | 2 | 31 | 35,46 | 1257 |
| 4 | 1,59 | 2,51 | 32 | 39,84 | 1587 |
| 5 | 1,78 | 3,16 | 33 | 44,64 | 1993 |
| 6 | 2 | 2,98 | 34 | 48,08 | 2312 |
| 7 | 2,24 | 5,01 | 35 | 56,82 | 3165 |
| 8 | 2,51 | 6,31 | 36 | 63,29 | 4006 |
| 9 | 2,82 | 7,94 | 37 | 70,92 | 5030 |
| 10 | 3,16 | 10 | 38 | 79,36 | 6298 |
| 11 | 3,55 | 12,59 | 39 | 89,29 | 7973 |
| 12 | 3,98 | 15,85 | 40 | 100 | 10000 |
| 13 | 4,47 | 19,96 | 41 | 112,23 | 12596 |
| 14 | 5,01 | 25,12 | 42 | 125,94 | 15861 |
| 15 | 5,62 | 31,65 | 43 | 141,24 | 19949 |
| 16 | 6,31 | 39,84 | 44 | 158,48 | 25116 |
| 17 | 7,08 | 48,08 | 45 | 177,94 | 31663 |
| 18 | 7,94 | 63,59 | 46 | 199,60 | 39840 |
| 19 | 8,91 | 79,36 | 47 | 223,71 | 50046 |
| 20 | 10 | 100 | 48 | 251,26 | 63132 |
| 21 | 11,22 | 125,94 | 49 | 281,69 | 79349 |
| 22 | 12,59 | 158,48 | 50 | 316,5 | 100 000 |
| 23 | 14,12 | 199,60 | 60 | 1 000 | 1 000 000 |
| 24 | 15,85 | 251,26 | 70 | 3165 | 10 000 000 |
| 25 | 17,79 | 316,50 | 80 | 10 000 | 100 000 000 |
| 26 | 19,96 | 398,4 | 90 | 31650 | 1 000 000 000 |
| 27 | 22,37 | 500,42 | 100 | 100 000 | 10 000 000 000 |
Как видите, чтобы напряжение увеличилось в три раза, мощность необходимо поднять в 10 раз. Впечатляющая разница. Эта таблица позволяет точно понять связь между этими величинами.
Но сигналы и величины не только увеличиваются, они могут и снижаться. Следующая таблица дана для падения значений относительно эталона.
| дБ | Снижение напряжения (силы тока) в разы | Снижение мощности (энергетической составляющей) в разы | дБ | Снижение напряжения (силы тока) в разы | Снижение мощности (энергетической составляющей) в разы |
|---|---|---|---|---|---|
| 0 | 1 | 1 | -8,0 | 0,398 | 0,159 |
| -0,1 | 0,989 | 0,977 | -9,0 | 0,355 | 0,126 |
| -0,2 | 0,977 | 0,955 | -10 | 0,316 | 0,1 |
| -0,3 | 0,966 | 0,933 | -11 | 0,282 | 0,0794 |
| -0,4 | 0,955 | 0,912 | -12 | 0,251 | 0,0631 |
| -0,5 | 0,944 | 0,891 | -13 | 0,224 | 0,0501 |
| -0,6 | 0,933 | 0,871 | -14 | 0,2 | 0,0398 |
| -0,8 | 0,912 | 0,832 | -15 | 0,178 | 0,0316 |
| -1,0 | 0,891 | 0,794 | -16 | 0,159 | 0,0251 |
| -1,5 | 0,841 | 0,708 | -18 | 0,126 | 0,0159 |
| -2,0 | 0,794 | 0,631 | -20 | 0,1 | 0,01 |
| -2,5 | 0,750 | 0,562 | -30 | 0,0316 | 0,001 |
| -3,0 | 0,668 | 0,501 | -40 | 0,01 | 0,0001 |
| -3,5 | 0,631 | 0,447 | -50 | 0,00316 | 0,00001 |
| -4,0 | 0,596 | 0,398 | -60 | 0,001 | 0,000001 |
| -4,5 | 0,562 | 0,355 | -70 | 0,000316 | 0,0000001 |
| -5,0 | 0,501 | 0,316 | -80 | 0,0001 | 0,00000001 |
| -6,0 | 0,501 | 0,251 | -90 | 0,0000316 | 0,000000001 |
| -7,0 | 0,447 | 0,2 | -100 | 0,00001 | 0,0000000001 |
Ослабление того или иного сигнала проще описывать в децибелах. Простые цифры легче запоминаются. Но иногда надо знать и реальный уровень мощности. Для этого используют таблицы (перевод дБ в мкВ)
Перевод ослабления сигнала в дБ в микровольты мкВ