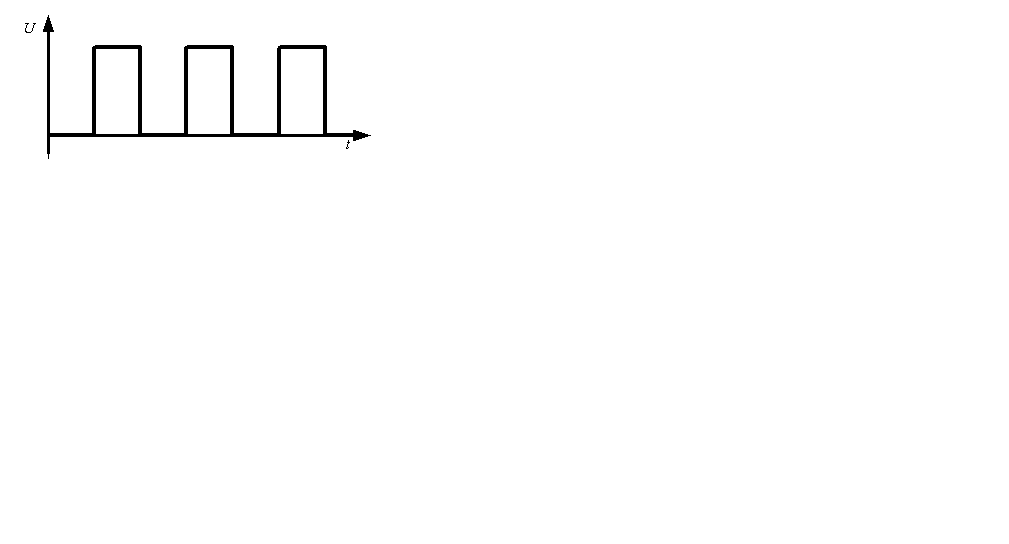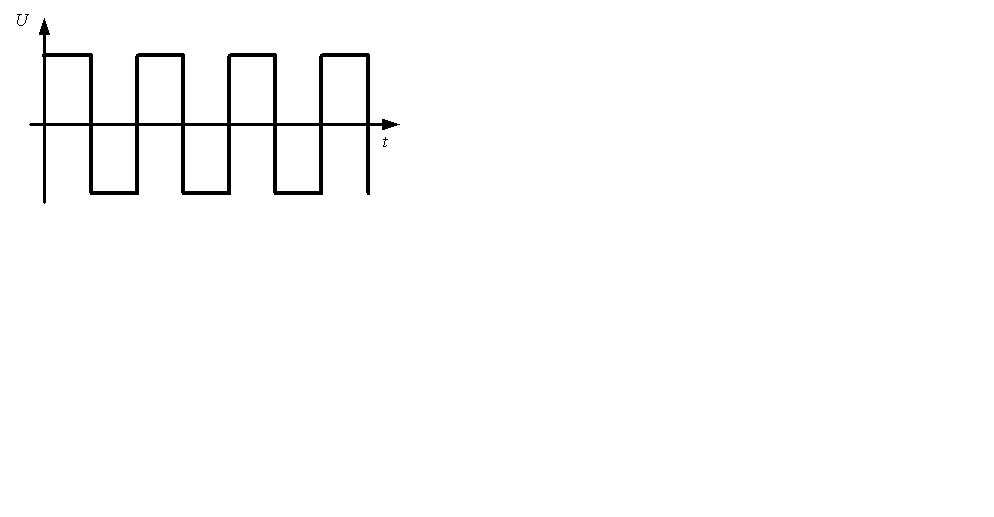в чем измеряется амплитуда сигнала
Измерение амплитуды сигналов
Амплитуду синусоидального сигнала, а также любого другого сигнала, можно оценивать не только как абсолютное максимальное его значение. Иногда пользуются понятием двойная амплитуда (амплитуда от пика до пика сигнала), которая, как нетрудно догадаться, равна удвоенной амплитуде. Иногда употребляют понятие эффективное значение, которое определяется следующим образом: UЭФФ = 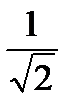
Измерение амплитуды в децибелах. Как сравнить амплитуды двух сигналов? Можно, например, сказать, что сигнал X в два раза больше, чем сигнал Y. Во многих случаях именно так и производят сравнение. Но очень часто подобные отношения достигают миллионов, и тогда удобнее пользоваться логарифмической зависимостью и измерять отношение в децибелах (децибел составляет одну десятую часть бела, но единицей «бел» никогда не пользуются). По определению отношение двух сигналов, выраженное в децибелах:
Хотя децибел служит для определения отношения двух сигналов, иногда эту единицу используют для измерения абсолютного, а не относительного значения амплитуды. Дело в том, что можно взять некоторую эталонную амплитуду и определять любую другую амплитуду в децибелах по отношению к эталонной. Известно несколько стандартных значений амплитуды, используемых для такого сравнения (эти значения не указываются, но подразумеваются); приведем некоторые из них: а) дБВ – эффективное значение 1 В; б) дБВт – напряжение, соответствую-щее мощности 1 мВт на некоторой предполагаемой нагрузке, для радиочастот это обычно 50 Ом, для звуковых частот – 600 Ом (напряжение 0 дБВт на этих нагрузках имеет эффективное значение 0,22 В и 0,78 В); в) дБп – небольшой шумовой сигнал, генерируемый резистором при комнатной температуре. Нужно обратить внимание на эталонную амплитуду 0 дБ: при использовании этого значения нужно не забывать его оговаривать, например «амплитуда 27 дБ относительно эффективного значения 1 В», или в сокращенной форме «27 дБ относительно 1 Вэфф» или пользоваться условным обозначением дБВ.
Импульсные сигналы
Электрическим импульсом называют напряжение или ток, отличающийся от нуля и имеющий постоянное значение лишь в течение короткого промежутка времени, меньшего или сравнимого с длительностью установления процессов в электрической системе, в которой действует этот ток или напряжение. В случае следующих друг за другом импульсов обычно предполагается, что интервал между ними существенно превышает длительность процессов установления.
В противном случае этот сигнал называют переменным напряжением или током сложной формы. С чисто математической точки зрения переходные процессы протекают, как известно, бесконечно долго, поэтому данное определение не совсем строго. Однако в реальных цепях длительность этих процессов не превышает 3τ, где τ – постоянная времени цепи, поэтому такое определение вполне допустимо.
Все многообразие электрических импульсов можно разделить на видеоимпульсы (рис. 1.2, а) и радиоимпульсы (рис. 1.2, б).
Связь между этими двумя типами импульсов состоит в том, что огибающая радиоимпульса представляет собой видеоимпульс. Частота синусоидального сигнала, которым заполнен видеоимпульс, называется частотой заполнения. Системы автоматики и управления оперируют в основном с видеоимпульсами, которые в дальнейшем будем называть просто импульсами.
Рис.1.2. Видео- и радиоимпульсы
На рис.1.3 приведен пример реального импульса.
Основными характеристиками и параметрами импульсов являются:
1.Амплитуда импульса Um = А;
2.Активная длительность импульса (измеряется на уровне 0,1А) tИ;
Рис. 1.3. Реальный прямоугольный импульс
5.Искажение вершины импульса ΔU;
6.Амплитуда обратного выброса Um ОБР;
7.Длительность обратного выброса tИ ОБР;
8.Мощность импульса P = W/tИ, где W – энергия импульса.
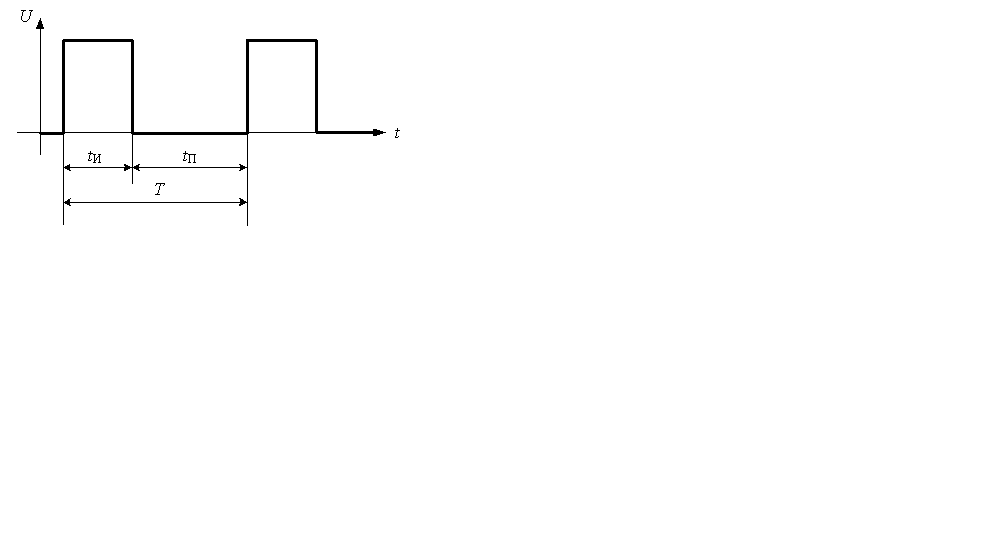
Периодически повторяющиеся импульсы образуют импульсную последовательность (рис.1.4). Она характеризуется следующими параметрами:
1.Частота импульсной последовательности ƒ = 1/Т, где T = tИ + tП;
2.Коэффициент заполнения γ = tИ/Т (диапазон изменения 0…1) и скважность Q = Т/tИ (диапазон изменения от 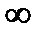
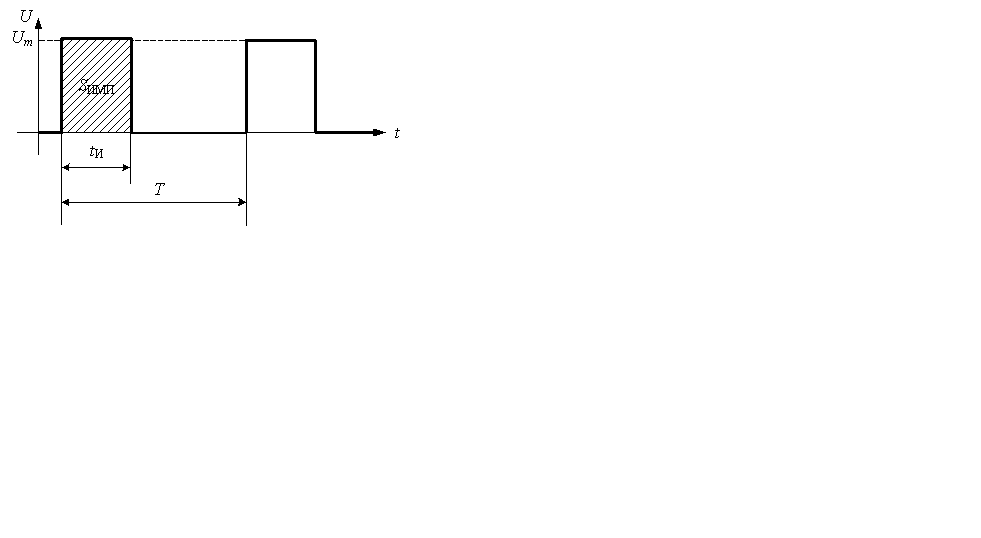
3.Среднее значение импульса (рис.1.5)
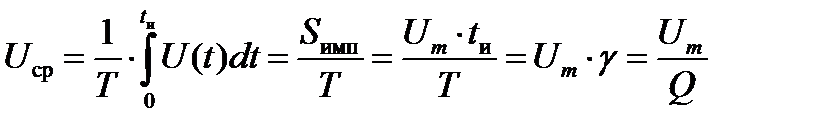
Рис. 1.4. Импульсная последовательность
Рис. 1.5. Определение среднего значения импульса
Импульсы имеют различную форму: прямоугольные, треугольные, трапецеидальные, экспоненциальные и др. (рис.1.6), так же могут быть однополярными (а) и разнополярными (б) (рис.1.7). Однополярные импульсы могут быть положительными и отрицательными. Для получения импульсных последовательностей различной формы, частоты и амплитуды применяют специальные генераторы.
Рис. 1.6. Треугольные (а), трапецеидальные (б), экспоненциальные (в) импульсы
Рис. 1.7. Однополярные положительные (а) и разнополярные (б) прямоугольные импульсы
При анализе работы систем автоматического управления и их отдельных элементов в качестве типовых возмущений используют одно из следующих.
Ступенчатое возмущение — мгновенное изменение воздействия на постоянную величину, чаще всего равную единице измерения (рис. 1.8, а). Физически система испытывает толчок. Аналитически
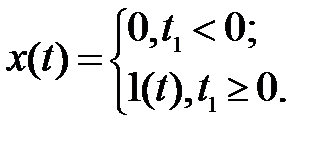
Единичный скачок в момент t1 пo отношению к моменту t0 аналитически записывается в виде 1( t1 – t0).
Рис.1.8. Типовые возмущения
2. Импульсное возмущение – это возмущение, полученное как последовательность двух одинаковых по величине, но противоположных по знаку ступенчатых возмущений, сдвинутых во времени. Особое значение имеет единичная импульсная или дельта-функция. Она обозначается 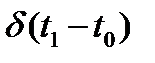
Дельта-функция обладает следующими свойствами:
Свойство (1.6) означает, что, несмотря на то, что функция имеет пренебрежимо малую длительность, площадь, ограниченная ей, имеет конечное значение, равное 1.
Свойство (1.7) означает, что импульсная функция 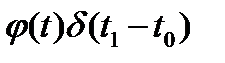
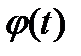
3. Периодическое возмущение. В ряде случаев периодическое возмущение является наиболее удобным для исследования. Так, для автоматических систем, работающих в режиме незатухающих колебаний, целесообразно проводить проверку их свойств под действием периодических возмущений.
Стандартным считается периодическое возмущение единичной амплитуды x(t)=sin ωt.
Аналоговые и дискретные сигналы имеют некоторые общие характеристики, с помощью которых они описываются. К таким характеристикам относятся: динамический диапазон, время установления и ширина спектра сигнала.
Динамический диапазон характеризуется отношением наибольшей мгновенной (пиковой) мощности к наименьшей (пороговой) мощности. Динамический диапазон является чисто физической характеристикой сигнала и не отражает смысла передаваемой с помощью этого сигнала информации. Однако его выбор определяется максимально допустимыми искажениями, которым может подвергаться сигнал в процессе формирования, передачи, обработки и приема без потери заключенной в нем информации. Наименьшая (пороговая) мощность сигнала определяется уровнем шумов и помех, которые неизбежно присутствуют в виде колебаний и скачков питающего напряжения, тепловых шумов, наводок от излучения, электромагнитных полей и т. д. При этом сигнал должен быть таким, чтобы он четко различался на уровне помех. Увеличение сигнала приводит к росту отношения сигнал-помеха, однако максимальное (пиковое) значение сигнала ограничивается как ростом затрачиваемой мощности, так и предельными характеристиками элементов и устройств, через которые происходит передача сигналов. Насыщение этих элементов приводит к искажению передаваемых сигналов, а значит и заключенной в них информации.
Время установления является динамической характеристикой сигнала и определяется временем, за которое сигнал достигнет своего установившегося значения. Этот параметр непосредственно связан с временными характеристиками устройств, формирующих сигнал, и определяется их инерционностью. Время установления можно характеризовать либо функцией времени (временной характеристикой), описывающей реальный процесс, либо функцией частоты (спектром, или рядом гармонических колебаний). При этом оба представления равносильны и взаимно дополняют друг друга, а переход от одного к другому осуществляется с помощью прямого и обратного преобразования Фурье или Лапласа.
Выбор того или иного способа описания (временного или частотного) определяется исключительно назначением устройства. При этом меняется лишь точка зрения на предмет, но не сам предмет, который представляет собой объективную реальность, независимую от способа ее описания.
Кроме рассмотренных общих характеристик, различные виды сигналов характеризуются рядом дополнительных, детализирующих их параметров. У постоянного напряжения – это амплитуда, у переменного напряжения – амплитуда, частота, фаза, среднее и действующее значения. Импульсные сигналы более сложны по форме, поэтому опишем их более детально.
Характеристики колебаний
Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени \(\large \Delta t\), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина \( \large x \). Тогда символом \( \large x_ <0>\) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):
Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
\( \large T \left( c \right) \) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):
Что такое частота
Обозначают ее с помощью греческой буквы «ню» \( \large \nu \).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
\( \large \nu \left( \frac<1>
Иногда в учебниках встречается такая запись \( \large \displaystyle \nu \left( c^ <-1>\right) \), потому, что по свойствам степени \( \large \displaystyle \frac<1>
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол \(\large 2\pi\) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный \(\large 2\pi\) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
\( \large \displaystyle \omega \left( \frac<\text<рад>>
Примечание: Величину \( \large \omega \) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за \(\large 2\pi\) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный \(\large 2\pi\) секунд?».
Обычная \( \large \nu \) и циклическая \( \large \omega \) частота колебаний связаны формулой:
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину \( \large \omega \), нужно сначала найти период T.
Затем, воспользоваться формулой \( \large \displaystyle \nu = \frac<1>
И только после этого, с помощью формулы \( \large \omega = 2\pi \cdot \nu \) посчитать циклическую \( \large \omega \) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину \( \large \omega \) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный \(\large 2\pi\), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).
Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, \(\large \varphi_ <0>\).
\(\large \varphi_ <0>\left(\text <рад>\right) \) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.
Рассмотрим теперь, как величина \(\large \varphi_ <0>\) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы \(\large \varphi_ <0>\) принимаем равной нулю.
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время \(\large \Delta t\), начальный угол \(\large \varphi_ <0>\) будет отличаться от нулевого значения.
Определим угол \(\large \varphi_ <0>\) с помощью графика колебаний.
Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина \(\large \varphi_ <0>\) — в радианах. Значит, нужно связать формулой кусочек времени \(\large \Delta t\) и соответствующий ему начальный угол \(\large \varphi_ <0>\).
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
\[\large T = 5 – 1 = 4 \left( \text <сек>\right)\]
Из графика следует, что период T = 4 сек.
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
Для этого используем формулу:
\(\large \displaystyle \frac<1> <4>\cdot 2\pi = \frac<\pi > <2>=\varphi_ <0>\)
Значит, интервалу \(\large \Delta t\) соответствует угол \(\large \displaystyle \frac<\pi > <2>\) – это начальная фаза для красной кривой на рисунке.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол \(\large \displaystyle \frac<\pi > <2>\) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая \(\large \varphi_ <0>= 0 \).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину \(\large \varphi_ <0>\) записываем со знаком «-».
Примечания:
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают \(\varphi\).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной \( \varphi_<0>\) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто \( \varphi\) фазой (рис. 10б) – это величина переменная.
Как на графике колебаний отметить фазу
На графике колебаний фаза \(\large \varphi\) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины \(\large \omega\) — циклическая частота и \(\large \varphi_<0>\) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу \(\large \varphi\), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
\( \large \varphi_<01>\) – для первого процесса и,
\( \large \varphi_<02>\) – для второго процесса.
Определим разность фаз между первым и вторым колебательными процессами:
Величина \(\large \Delta \varphi \) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
\( \large T \left( c \right) \) – время одного полного колебания (период колебаний);
\( \large N \left( \text <шт>\right) \) – количество полных колебаний;
\( \large t \left( c \right) \) – общее время для нескольких колебаний;
\(\large \nu \left( \text <Гц>\right) \) – частота колебаний.
\(\large \displaystyle \omega \left( \frac<\text<рад>>
\(\large \varphi_ <0>\left( \text <рад>\right) \) — начальная фаза;
\(\large \varphi \left( \text <рад>\right) \) – фаза (угол) в выбранный момент времени t;
\(\large \Delta t \left( c \right) \) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.