гексагон что это за фигура
Правильный шестиугольник
Содержание
Свойства
Построение
Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.
Правильный шестиугольник в природе, технике и культуре
Примечания
Смотрите также
Ссылки
 |
 Правильные многоугольники Правильные многоугольники | |
|---|---|
| Основные | Треугольник • Квадрат • Пятиугольник • Шестиугольник • Семиугольник • Восьмиугольник • Девятиугольник • Семнадцатиугольник • 257-угольник • 65537-угольник |
| См. также | Многоугольник • Теорема Гаусса — Ванцеля |
Полезное
Смотреть что такое «Правильный шестиугольник» в других словарях:
Шестиугольник — Правильный шестиугольник Шестиугольник многоугольник с шестью углами. Также шестиугольником называют всякий предмет такой формы. Сумма внутренних углов выпуклого шестиугольника р … Википедия
Шестиугольник Сатурна — Гексагональное устойчивое атмосферное образование на северном полюсе Сатурна, открытое аппаратом Вояджер 1 и наблюдаемое снова в 2006 году а … Википедия
Правильный семиугольник — Правильный семиугольник это правильный многоугольник с семью сторонами. Содержание … Википедия
Правильный треугольник — Правильный треугольник. Правильный (или равносторонний) треугольник это правильный многоугольник с тремя сторонами, первый из правильных многоугольников. Все стороны … Википедия
Правильный девятиугольник — это правильный многоугольник с девятью сторонами. Свойства Правиль … Википедия
Правильный 17-угольник — Правильный семнадцатиугольник геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности. Содержание 1… … Википедия
Правильный семнадцатиугольник — геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности. Содержание … Википедия
Правильный восьмиугольник — (октагон) геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов и все углы и стороны равны между собой … Википедия
Правильный 65537-угольник — 65537 угольник или окружность? Правильный 65537 угольник (шестѝдесятипятиты̀сячпятисо̀ттридцатисемиугольник) геометрическая фигура из группы правильных многоугольников, состоящая из 65537 … Википедия
Шестиугольник, виды, свойства и формулы
Шестиугольник, виды, свойства и формулы.
Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.
Шестиугольник, выпуклый и невыпуклый шестиугольник:
Шестиугольник – это многоугольник с шестью углами.
Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.
Шестиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый шестиугольник – это шестиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Рис. 1. Выпуклый шестиугольник

Сумма внутренних углов любого выпуклого шестиугольника равна 720°.

Правильный шестиугольник (понятие и определение):
Правильный шестиугольник (гексагон) – это правильный многоугольник с шестью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный шестиугольник – это шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.
Рис. 3. Правильный шестиугольник
Правильный шестиугольник имеет 6 сторон, 6 углов и 6 вершин.
Правильный шестиугольник можно построить с помощью циркуля и линейки.
Свойства правильного шестиугольника:
1. Все стороны правильного шестиугольника равны между собой.
2. Все углы равны между собой и составляют 120°.
Рис. 4. Правильный шестиугольник
3. Сумма внутренних углов любого правильного шестиугольника равна 720°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного шестиугольника O.
Рис. 5. Правильный шестиугольник
5. Количество диагоналей правильного шестиугольника равно 9.
Рис. 6. Правильный шестиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.
Рис. 7. Правильный шестиугольник
7. Правильные шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).
8. Радиус описанной окружности правильного шестиугольника и его сторона равны.
Гексагон
Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.
При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
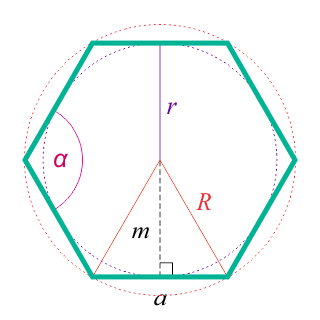
Свойства правильного шестиугольника
Внутренние углы Внутренние углы в правильном шестиугольнике равны \(120^\circ\) :
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Радиус вписанной окружности правильного шестиугольника равен апофеме:
\(r = m = a\large\frac<<\sqrt 3 >><2>\normalsize\)
Радиус описанной окружности равен стороне правильного шестиугольника:
Периметр правильного шестиугольника
Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны
\(S = pr =
где \(p\) − полупериметр шестиугольника.
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Гексагон вокруг нас
В окружающей нас природе прослеживается строгая геометрия. Особое место отдано гексагону — правильному шестиугольнику. Эта фигура в тренде у насекомых, животных и даже неживой материи благодаря своим преимуществам в плане соответствия физическим законам.
Гексагон и пчёлы
Пчелиные соты, имеющие форму призмы с основанием в виде того самого гексагона, производят впечатление настоящего чуда с точки зрения инженерии. В том числе потому что:
Как столь сложную конструкцию выстраивают без расчетов и чертежей обычные насекомые? Тем более, что это — огромный коллектив, который работает одновременно, умудряясь как-то координировать свои действия. И в результате делает соты абсолютно одинаковыми.
По мнению Паппа Александрийского, философа из Древней Греции, пчелам свойственно «геометрическое предвидение». Данное им Господом. В 19-м столетии в «Монографии о пчёлах Англии» энтомолог У. Кёрби называл пчёл «математиками от Бога».
Ч. Дарвин был в этом совсем не уверен. Потому придумывал разнообразные эксперименты, призванные определить, строят ли пчёлы столь идеальные по геометрии соты, на основе врожденных или приобретенных способностей.
Почему шестиугольник?
Для геометрии это — простой вопрос. Когда нужно сложить ряд ячеек с одинаковыми размерами и формой так, чтобы заполнить ими определенную плоскость как можно полнее, подходят лишь 3 типа «правильных» (имеющих равные стороны и углы) фигур. То есть, речь идет о равносторонних:
В «личном» же первенстве данных вариантов, при равной площади, шестиугольникам потребуется наименьшая общая длина перегородок. Отсюда у пчелиного предпочтения гексагонов наблюдается непробиваемая логика. Чем меньше длина — тем меньше и воска, и труда.
Именно Дарвин первым выявил эту закономерность. А также был уверен, что благодаря естественному отбору, пчёлы получили инстинкты для создания ячеек наиболее рациональной формы. Однако современная наука, признавая за пчёлами особые способности в измерении толщины стенок или углов, обращает внимание на распространенность шестиугольников в природе вообще, а не только в ульях.
Пузыри на воде
Стоит подуть на пузырьки воздуха на водной поверхности, согнав их близко друг к другу, как они приобретают шестиугольную форму. И чем плотнее пузыри сгруппированы, тем явнее становится их шестиугольность.
А ведь при этом нет воздействия каких-либо организмов, работы над склейкой этих пузырей, подобной строительству пчел своих сот. Получившийся рисунок обязан своим появлением только физическим закономерностям.
Причина такой формы пузырей и образования именно таких «развилок» между мыльными стенками в том, что природу не менее пчёл заботит экономия сил и средств. Пузыри из мыльной пленки состоят из воды и слоя мыльных молекул. Поверхность жидкости под воздействием поверхностного натяжения сжимается так, чтобы занимать как можно меньшую площадь. Ровно как в случае с каплями дождя, принимающими при падении форму, стремящуюся к сферической. Потому что сфера отличается наименьшей площадью поверхности среди всех фигур с тем же объёмом. И на восковых листках водяные капли сжимаются до маленьких бусинок согласно все тому же закону.
То есть, именно поверхностным натяжением обусловлен узор, образуемый пузырями или пеной. Здесь прослеживается все то же стремление к конструкции, обеспечивающей минимальность общего поверхностного натяжения. А следовательно, мыльная мембрана обязана иметь и минимальную площадь. Причем стенки пузырей должны иметь конфигурацию, которая обязана обладать и механической прочностью. Такой, чтобы натяжение на перекрещивающихся направлениях имело идеальную сбалансированность. Точно так же, как обязателен баланс при возведении здания соборного типа.
Однако ошибочно принимать соты за этакое застывшее множество восковых пузырей. Потому что тогда будет трудно дать объяснение, каким образом подобные 6-угольные ячейки бумажные ячейки строят осы, создающие свои гнёзда из комков жёваной древесины. Во-первых, поверхностному натяжению здесь особая роль явно не принадлежит. А во-вторых, очевидно, что различные виды ос обладают разными врожденными инстинктами в плане «архитектурных школ», которые различаются весьма значительно.
Морской мир
У черепахи в центре панциря кожа также обладает 6-угольной формой. Именно потому что так наиболее эффективно можно покрыть плоскую поверхность. Для изогнутой же гексагоны не столь хороши. А панцирь черепах является именно таким. Отчего в нём присутствует кольцо и 5-угольников и вовсе неправильных фигур.
Вымершие уже кораллы под названием Cyathophyllum hexagonum даже имя своё получили благодаря 6-угольной форме. И такая группа водорослей, как диатомовые тоже обладают формой 6-угольника. Однако, сложно найти биологическую структуру, которая отличается более явной «гексагонностью», как глаз стрекозы.
Стрекоза и гексагон
Стрекозиный глаз включает порядка 30 тысяч 6-угольников, которые ещё и переплетены в умопомрачительной структуре. По сути, этот оптический аппарат, считающийся одним из лучших среди животных, состоит из гексагонов. При этом, лишь 3 из 6-угольников соприкасаются в любой вершине или определенной точке пересечения.
Напомним, что речь идет только о двух больших сложных глазах, а не о дополнительных трёх — с обычными линзами. Причём множество насекомых имеют глаза 6-угольной формы. И абсолютно всегда соблюдается тенденция, что только 3 стенки могут встретиться в одной вершине. А если отойти от мира биологии, обнаруживается, что такому же правилу подчинено всё, где встречаются гексагоны.
Вулканы
Извержения некоторых вулканов (в первую очередь — базальтовых пород) порождают изумительные образования 6-угольной формы. Озадачивая людей в течении столетий, такие гексагоны встречаются по всей планете: и примерно 6-угольные, и совершенно 6-угольные.
Наиболее известны два из них:
Снег кружится…
… летает и тает. Но, до того, как растаять, успевает подарить нам чудное зрелище — снежинку. При уникальности каждой из них абсолютно все обладают шестью сторонами или точками. В этой форме снежинок отражается её внутренняя структура. Именно благодаря гексагональной структуре молекулы воды группируются максимально эффективно.
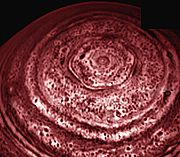
Самый крупный гексагон
На макроуровне одним из наиболее известных 6-угольников считается гигантское облако гексагональной формы на северном полюсе планеты Сатурн. Длина его составляет примерно 14,5 тыс. км, что больше диаметра Земли. А каждая сторона Гексагона Сатурна (так его астрономы и называют) достигает в длину 13,8 тыс. км.
Этот гексагон образуют газы, слой которых, предположительно достигает толщины в 300 км и движется со скоростью 320 км/ч. Облако вращается — 1 оборот за 10 ч. 39 мин. Не в пример остальным облакам на Сатурне, это не перемещается, постоянно находясь на одном месте.
Над южным полюсом планеты ничего подобного нет. Но есть огромная воронка в атмосфере, ровно такая, как в центре Гексагона Сатурна.
На клеточном уровне
Вышеописанные правила работают и в узорах, присущих живым организмам. Так, из групп 6-угольных ячеек состоит не только фасеточный глаз мухи, но и в каждой такой ячейке обнаруживаются гроздья из 4-х светочувствительных клеток, напоминающие мыльный пузырь.
Для строительства подобных гексагонов не требуется сложных генетических инструкций. Физические законы всё сделают сами. Пористую совокупность ячеек представляет собой экзоскелет такого животного, как морской ёж Cidaris rugosa. На этой защитной раковине размещены опасные на вид колючки из минерала, из которого состоят мел и мрамор. Благодаря открытой решетчатой структуре этот материал отличается прочностью и малой массой, подобно пенометаллу, применяемому в авиапромышленности.
Экзоскелеты некоторых видов морских губок образуют минеральные стержни, которые соединены подобно «паутинке» с детских площадок. Также они очень напоминают по форме пузыри в мыльной пене. Без малейшего допущения «случайного совпадения», потому что такая архитектура диктуется поверхностным натяжением.
Этот процесс, называемый биоминерализацией, даёт особенно впечатляющие результаты и у других морских животных, например — диатомей и лучевиков. Ряд из них обладают аккуратными экзоскелетами из ячеек в форме гексагонов, этакими минеральными «морскими сотами». Естествоиспытатель, философ и художник 19-го столетия Э. Геккель, увидев их в микроскопе, использовал эти формы, как главное украшение своей серии рисунков «Красота форм в природе», оказавшей сильное влияние на многих художников до нашего времени.
Геккель считал такие конструкции доказательством истинной креативности природы, её предпочтением таких узоров и порядков, которое встроено в основу естественных законов. Упорядоченность остается неудержимым импульсом живой и неживой природы. Именно поэтому мы и выбрали для нашей компании гордое имя «Гексагон». Как символ:
И этими же принципами руководствуемся при создании нашей продукции.
Шестиугольник, виды, свойства и формулы




Шестиугольник, выпуклый и невыпуклый шестиугольник:
Шестиугольник – это многоугольник с шестью углами.
Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.
Шестиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый шестиугольник – это шестиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Рис. 1. Выпуклый шестиугольник
Рис. 2. Невыпуклый шестиугольник
Сумма внутренних углов любого выпуклого шестиугольника равна 720°.
Размеры
Чтобы отвертка прослужила долго, и не стерлась, важно выбрать правильный размер инструмент с нужным наконечником.
Для каждого вида разработаны специальные стандарты размеров, и присвоены им номерные обозначения.
Шлицевые отвертки с плоской формой наконечника могут иметь ширину от 2 до 18 мм, а крестообразные модели идут с нумерацией от 0 до 4.
Все номерные виды рассчитаны на определенный диаметр наружной резьбы:
• № 0 – до двух мм; • № 1 – от двух до трех мм; • № 2 – от трех до пяти мм; • № 3 – от пяти до семи мм и т.д.
Размеры стержня зависят от номера отвертки.
Так, например, нулевая отвертка имеет диаметр стержня 4 миллиметра при длине до 80 миллиметров.
По мере возрастания номера увеличивается диаметр и длина стержня.
Правильный шестиугольник (понятие и определение):
Правильный шестиугольник (гексагон) – это правильный многоугольник с шестью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный шестиугольник – это шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.
Рис. 3. Правильный шестиугольник
Правильный шестиугольник имеет 6 сторон, 6 углов и 6 вершин.
Углы правильного шестиугольника образуют шесть равносторонних треугольников.
Правильный шестиугольник можно построить с помощью циркуля и линейки.
Торцевые гаечные ключи
Этот вид ключей представляет собой полую трубку или цилиндр с углублениями на обоих концах. Торцевые ключи бывают двух типов:
Г-образные торцевые ключи
Они имеют одинаковый размер на обоих краях рабочих частей. Это сделано с тем расчетом, что гайка (или болт) могут находиться глубоко от поверхности и тогда используется длинная часть ключа, но при этом необходимо приложить больше усилий (из-за маленького рычага). Если деталь находится неглубоко, тогда используется короткая часть ключа, соответственно из-за большего рычага усилий прикладывается меньше.
I-образные гаечные ключи
Выглядят как полый цилиндр с рабочей частью разного размера на обоих концах. Работать таким ключом приходиться, используя рычаг (вороток) который вставляется в сквозное отверстие в корпусе ключа.
Виды молотков и их назначение
Шестигранные ключи
Этот вид ключей имеет Г-образную форму и используется для работы с болтами (шурупами, винтами) имеющими не внешние грани, а внутренние. В основном применяются в основном при сборке мебели, ремонте бытовой технике и подобных работах.



Свойства правильного шестиугольника:
1. Все стороны правильного шестиугольника равны между собой.
a1 = a2 = a3 = a4= a5= a6.
2. Все углы равны между собой и составляют 120°.
α1 = α2 = α3 = α4 = α5 = α6 = 120°.
Рис. 4. Правильный шестиугольник
3. Сумма внутренних углов любого правильного шестиугольника равна 720°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного шестиугольника O.
Рис. 5. Правильный шестиугольник
5. Количество диагоналей правильного шестиугольника равно 9.
Рис. 6. Правильный шестиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.
Рис. 7. Правильный шестиугольник
7. Правильные шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).
8. Радиус описанной окружности правильного шестиугольника и его сторона равны.
Рис. 8. Правильный шестиугольник
Накидные ключи
У этих ключей рабочая часть имеет фору кольца с гранями на внутренней стороне. Его конструкция более надежна чем у рожковых ключей, так как деталь охватывается по всей поверхности (то есть как минимум в шести местах), что практически исключает деформацию углов. Накидные ключи существуют с двумя типами внутреннего профиля – с 6-и гранным профилем и 12-и гранным профилем. Профилем с 12-ю гранями работать в ограниченном пространстве удобней, так как ему достаточно поворота на 30 градусов, к ключу с 6-и гранным профилем необходимо 60 градусов поворота.
Чистый двор и дом — мойка высокого давления!
Более распространенны ключи с наклонной головкой, когда рабочая часть находится под небольшим углом к рукоятке. Накидные ключи выпускаются разного размера, как и рожковые ключи.
Правильный шестиугольник в природе, технике и культуре:
Пчелиные соты имеют форму правильного шестиугольника.
Графит, графен имеют гексагональную кристаллическую решетку.
Гигантский гексагон – атмосферное явление на Сатурне – имеет форму правильного шестиугольника.
Рис. 9. Гигантский гексагон на Сатурне
Сечение гайки и многих карандашей имеет вид правильного шестиугольника.
Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.
Панцирь черепахи состоит из шестиугольников.
Гексагоном иногда называют материковую часть Франции, потому что её географические очертания напоминают данную геометрическую фигуру.
Рис. 10. Материковая часть Франции
Виды отверток и их назначение
Универсальная отвертка слесарная – это инструмент, который есть практически в каждом доме.
Благодаря отвертке можно выполнять ремонтные работы разной степени сложности, главное знать, какой тип и диаметр подойдет в каждом конкретном случае.
О том, какие бывают отвертки можно узнать, если детальнее углубиться в тему.
Отличительной особенностью всех видов является разное толщина стержня.
Читать также: Как проверить акб без нагрузочной вилки
Наиболее популярными считают отвертки с круглым и квадратным сечением, с прямым или крестообразным шлицем.
Однако технический прогресс не стоит на месте и наряду с новыми видами крепежа появляются профессиональные отвертки для вкручивания болтов, шурупов и прочих элементов.
Все это делается для того, чтобы облегчить работу потребителям.
• На данный момент кроме универсальных моделей существует еще несколько модернизированных видов отверток для проведения разных работ.
Например, переставная отвертка отличается своей универсальностью, т.к. с одной стороны стержня она плоская, а с другой крестовая.
Некоторые переставные модели имеют несколько разных наконечников, что повышает универсальность инструмента.
• Точная или как ее еще называют, тонкая отвертка – подойдет для ремонта мобильных телефонов, ее маркировка соответствует нулевому обозначению.
Изделие производят с малым размером шлица, не более 2мм, что позволяет выполнить точную работу с мелкими деталями.
• Особые эргономичные свойства приобрела двухкомпонентная отвертка, ее отличительной особенностью стала прочная рукоять из комбинированных материалов.
Для покрытия рукояти использовали полипропилен и резину.
Двухкомпонентное покрытие способствует надежному захвату, чтобы изделие уже не могло выскользнуть из рук.
• Для работы с тонкими деталями используют часовые отвертки, с их помощью ремонтируют часовые механизмы.
Размер наконечника изделия – не более миллиметра.
На этом классификация профессиональных монтажных отверток не заканчивается, существует еще много разновидностей моделей, предназначенных для определенных целей.
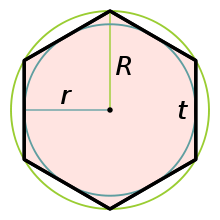
Формулы правильного шестиугольника:
Пусть a – сторона шестиугольника, r – радиус окружности, вписанной в шестиугольник, R – радиус описанной окружности шестиугольника, P – периметр шестиугольника, S – площадь шестиугольника.
Формулы периметра правильного шестиугольника:
Формулы площади правильного шестиугольника:
Формула радиуса окружности, вписанной в правильный шестиугольник:
Формула радиуса окружности, описанной вокруг правильного шестиугольника:
Маркировка и размеры [ править | править код ]
Ключи и отвёртки имеют маркировку T
или
TX
с номером шлица — 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 15, 20, 25, 27, 30, 40, 45, 50, 55, 60, 70, 80, 90, 100.
Ключи и отвёртки со шлицом Torx Tamper Resistant
после основной маркировки дополнительно обозначаются
TR
.
У ключей и отвёрток со шлицом Torx Plus
сначала указывается номер шлица, а после — вместо
T
или
TX
обозначается буквами
IP
.
Ключи и отвёртки со шлицом Torx Plus Tamper Resistant
после основной маркировки дополнительно обозначаются
TS
.
Размер определяется по диаметру окружности описанной по вершинам звездочки инструмента (для версии E — болта).
Приблизительные размеры и моменты затяжки [3]
| дюймы | мм | Н•м | ||
| T1 | 0,031″ | 0,81 | 0,02 — 0,03 | |
| T2 | 0,036″ | 0,93 | 0,07 — 0,09 | |
| T3 | 0,046″ | 1,10 | 0,14 — 0,18 | |
| T4 | 0,050″ | 1,28 | 0,22 — 0,28 | |
| T5 | 0,055″ | 1,42 | 0,43 — 0,51 | |
| T5.5 [4] [5] [6] | ||||
| T6 | 0,066″ | 1,70 | 0,75 — 0,90 | |
| T7 | 0,078″ | 1,99 | 1,4 — 1,7 | |
| T8 | 0,090″ | 2,31 | 2,2 — 2,6 | |
| T9 | 0,098″ | 2,50 | 2,8 — 3,4 | |
| T10 | 0,107″ | 2,74 | 3,7 — 4,5 | |
| T15 | 0,128″ | 3,27 | 6,4 — 7,7 | |
| T20 | 0,151″ | 3,86 | 10,5 — 12,7 | E4 |
| T25 | 0,173″ | 4,43 | 15,9 — 19 | E5 |
| T27 | 0,195″ | 4,99 | 22,5 — 26,9 | |
| T30 | 0,216″ | 5,52 | 31,1 — 37,4 | E6 |
| T35 [7] [8] [9] | ||||
| T40 | 0,260″ | 6,65 | 54,1 — 65,1 | E8 |
| T45 | 0,306″ | 7,82 | 86 — 103,2 | |
| T47 [10] [11] | GM-Style | |||
| T50 | 0,346″ | 8,83 | 132 — 158 | E10 |
| T55 | 0,440″ | 11,22 | 218 — 256 | E12 |
| T60 | 0,519″ | 13,25 | 379 — 445 | E16 |
| T70 | 0,610″ | 15,51 | 630 — 700 | E18 |
| T80 | 0,690″ | 17,54 | 943 — 1048 | E20 |
| T90 | 0,784″ | 19,92 | 1334 — 1483 | |
| T100 | 0,871″ | 22,13 | 1843 — 2048 | E24 |
Размеры внешних шлицов Torx
| Номер | Размер [12] | Стандартный болт [13] | ||
| дюймы | мм | SAE | метрический | |
| E4 | 0,15″ | 3,8 | #6 | M3 |
| E5 | 0,18″ | 4,7 | #8 | M4 |
| E6 | 0,22″ | 5,6 | #10 | M5 |
| E7 | 0,24″ | 6,1 | ||
| E8 | 0,29″ | 7,4 | 1/4″ | M6 & M7 |
| E10 | 0,36″ | 9,3 | 5/16″ | M8 |
| E12 | 0,43″ | 11,1 | 3/8″ | M10 & M11 |
| E14 | 0,50″ | 12,8 | 7/16″ | M12 |
| E16 | 0,57″ | 14,7 | 1/2″ | |
| E18 | 0,65″ | 16,6 | 9/16″ | M14 |
| E20 | 0,72″ | 18,4 | 5/8″ | M16 |
| E24 | 0,87″ | 22,1 | 3/4″ | M18 & M20 |
| E28 | 7/8″ | M22 | ||
| E32 | 1″ | M24 & M27 | ||
| E36 | 1-1/8″ | M30 | ||
| E40 | 1-1/4″ | M33 | ||
| E44 | 1-3/8″ | M36 | ||
Использование [ править | править код ]
Крепёж со шлицом Torx обычно используется в технике: автомобилях, велосипедах, тормозных системах, разнообразных сборных металлических конструкциях, жёстких дисках компьютеров, банкоматах, потребительской электронике и топливной аппаратуре.
Неизвестно, специально это было сделано или нет, но размеры Torx коррелируются с размерами инбусовых ключей и позволяют выкрутить сорванный шестигранный шлиц. При срыве шлица в образованное отверстие забивается инструмент Torx и практически со стопроцентным результатом позволяет выкрутить сорванный болт или винт.
Следует отметить, что при работе с Torx необходимо учитывать следующие особенности:
Несоблюдение этих правил зачастую ведёт к разрушению головки болта и, как следствие, к необоснованной критике Torx.