что нужно знать в 7 классе по алгебре

Краткий курс алгебра 7 класс

Краткий курс в определениях и формулах 7 класс.Удобно для повторения и подготовки к экзаменам.

Просмотр содержимого документа
«Краткий курс алгебра 7 класс»

Числовые и буквенные выражения.

Решение задачи разбивается на 3 этапа а). Составление математической модели; б). Работа с математической моделью; в).Ответ на вопрос задачи.

Существует несколько видов моделей: Словесная модель(реальные ситуации описываются словами), алгебраическая модель (алгебраически ), геометрическая модель ( в геометрии и графики).

Линейные уравнения с одним неизвестным.

Алгоритм решения линейного уравнения ах+б=0 в случае когда а ≠ 0.

Алгоритм решения линейного уравнения ах+б=сх+д (а≠ с )

Перенести все члены уравнения из правой части в левую с противоположными знаками.

Получится уравнение вида кх+м=0.

называют координатной прямой или координатной осью.

Алгоритм отыскания координат точки М, заданной в системе координат хОу.

Алгоритм построения точки М(а;б) в прямоугольной системе координат хОу.

Построить прямую у=б.

Найти точку пересечения построенных прямых – это и будет точка М(а;б).

Линейное уравнение с двумя переменными.

Графиком линейного уравнения является прямая.

Придать переменной х конкретное значение х=х₁ ( х=0 ) найти из уравнения ах₁+бу+с=0 соответствующее значение у=у₁.

Придать переменной у конкретное значение у=у₂ ( у=0 ) найти из уравнения ах+бу₂+с=0 соответствующее значение х=х₂.

Построить на координатной плоскости хОу точки (х₁;у₁) и (х₂;у₂).

Провести через эти две точки прямую – она и будет графиком уравнения ах+бу+с=0.

У линейной функции х- независимая переменная ( или аргумент ), у – зависимая переменная ( или функция ).

Теорема 2. Графиком линейной функции у= кх +м является прямая.

Если к › 0 то функция у=кх + м возрастает.

Если к ‹ 0 то функция у=кх + м убывает.

Коэффициент К в записи у=кх называют угловым коэффициентом.

Системы двух линейных уравнений с двумя переменными.

Пару значений (х;у), которая одновременно является решением и первого и второго уравнений системы, называют решением системы.

Графический метод решения системы.

Если прямые совпадают, то система имеет бесконечное множество решений ( система неопределенна)

Алгоритм решения системы двух уравнений с двумя переменными методом подстановки.

Выразить У через Х из первого уравнения системы.

Подставить полученное на первом шаге выражение вместо У во второе уравнение системы.

Решить полученное на втором шаге уравнение относительно Х.

Метод алгебраического сложения.

Степень с натуральным показателем.

Степенью числа а с показателем 1 называют само это число.

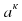
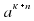
Теорема 1. Для любого числа а и любых натуральных чисел n и к справедливо равенство *=( При умножении степеней с одинаковыми основаниями показатели складываются)

Теорема 3. Для любого числа а и любых натуральных чисел n и к справедливо равенство = ( При возведении степи в степень показатели умножаются).

Если а ≠ 0, то 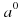= 1.

Чтобы привести одночлен к стандартному виду, нужно: а) перемножить все числовые множители и поставить их произведение на первое место; б) перемножить все имеющиеся степени с одним буквенным основанием; в) перемножить все имеющиеся степени с другим буквенным основанием и т.д.

Алгоритм сложения одночленов.

Привести все одночлены к стандартному виду.

Найти сумму коэффициентов подобных одночленов.

Многочлены. Арифметические операции над многочленами.

Многочленом называют сумму одночленов.

Чтобы записать алгебраическую сумму нескольких многочленов в виде многочлена стандартного вида, нужно раскрыть скобки и привести подобные члены.

Чтобы умножить многочлен на одночлен, нужно каждый член многочлена умножить на этот одночлен и полученные произведения сложить.

Чтобы умножить многочлен на многочлен, нужно умножить каждый член одного многочлена поочерёдно на каждый член другого многочлена и полученные произведения сложить.

Квадрат суммы двух выражений равен сумме их квадратов плюс их удвоенное произведение. =+2аб+

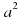
Квадрат разности двух выражений равен сумме их квадратов минус их удвоенное произведение.=-2аб+

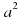
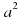
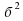
Разность квадратов двух выражений равна произведению суммы этих выражений на их разность. — = (а- б)(а+ б).

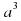
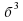
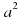
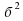
Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы. — = (а- б)(+ аб+).

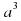
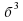
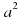
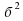
Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности. + = (а + б)(— аб+).

Разложение многочленов на множители.

Способ вынесения общего множителя за скобки.

Сокращение алгебраических дробей.

Функция у = и её график.

Графиком функции у = является парабола.

Источник

Что нужно знать в 7 классе по алгебре

(остальные материалы готовятся к публикации)

Глава 3. Алгебра 8 класс

(остальные материалы готовятся к публикации)

Глава 4. Алгебра 9 класс

(остальные материалы готовятся к публикации)

Глава 5. Материалы для подготовки к ОГЭ

Глава 6. Алгоритмы решения задач по алгебре

Электронные формы учебников для 6-9 классов (ссылки):

Алгебра (от араб. الْجَبْر‎, «аль-джабр» — восполнение) — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики. Слово «алгебpа» также употребляется в общей алгебре в названиях различных алгебраических систем. В более широком смысле под алгеброй понимают раздел математики, посвящённый изучению операций над элементами множества произвольной природы, обобщающий обычные операции сложения и умножения чисел.

Алгeбра как раздел математики традиционно включает следующие категории: Элементарная, Общая, Универсальная, Линейная (включая матрицы) и Алгебраическая комбинаторика.

Элементарная алгебpа, которая изучает свойства операций с вещественными числами. В ней постоянные и переменные обозначаются буквенными символами. Элементарная алгeбpа содержит правила преобразования математических выражений и уравнений с использованием этих символов. Обычно преподаётся в школе под названием aлгебра.

Источники идей и цитат для конспектов по Алгебре:

(с) Цитаты из вышеуказанных учебных пособий использованы на сайте в незначительных объемах, исключительно в учебных и информационных целях (пп. 1 п. 1 ст. 1274 ГК РФ).

Источник

Что нужно знать в 7 классе по алгебре

Выражения и их преобразования

☑ 1. Степенью числа а с натуральным показателем n, большим 1, называют произведение n множителей, каждый из которых равен а: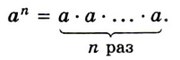
Степенью числа а с показателем 1 называют само число а: а 1 = а.
Степень числа а ≠ 0 с показателем 0 равна 1: а 0 = 1.

☑ 2. Свойства степеней с натуральными показателями:

а m • а n = а m+n

При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.

(а m ) n = а mn

При возведении степени в степень основание оставляют прежним, а показатели перемножают.

(ab) n = а n b n

При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.

Степенью одночлена называют сумму показателей степеней всех переменных, входящих в одночлен. Например, степень одночлена –8а 2 b 4 равна 6.

☑ 4. Многочленом называют сумму одночленов. Например, 3х 5 – 4х 2 + 1, 7a 3 b – ab 2 + ab + 6 —многочлены. Одночлены считают многочленами, состоящими из одного члена.

Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Например, степень многочлена 5х 3 у + 3х 2 у 5 + ху равна степени одночлена 3х 2 у 5 , т. е. равна 7.

Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.

☑ 5. При сложении многочленов пользуются правилом раскрытия скобок : если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки. Например,

(3аb + 5с 2 ) + (ab – с 2 ) = 3ab + 5с 2 + ab – с 2 = 4аb + 4с 2

При вычитании многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки. Например,

(6x 2 – у) – (2x 2 – 8у) = 6х 2 – у – 2х 2 + 8у = 4х 2 + 7у

Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Например,

а 2 (3аb – b 3 + 1) = 3а 3 b – а 2 b 3 + а 2

Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. Например,

(5х – 1)(3х + 2) = 15x 2 – Зx + 10x – 2 = 15x 2 + 7x – 2

☑ 6. Формулы сокращённого умножения:

(а + b) 2 = а 2 + 2аb + b 2

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.

(а – b) 2 = а 2 – 2аb + b 2

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.

(а + b) 3 = а 3 + 3а 2 b + 3ab 2 + b 3

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

(а – b) 3 = а 3 – 3а 2 b + Заb 2 – b 3

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(а – b)(а + b) = а 2 – b 2

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

а 3 + b 3 = (а + b)(a 2 – аb + b 2 )

Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

а 3 – b 3 = (а – b)(a 2 + ab + b 2 )

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

☑ 7. Разложением многочлена на множители называют представление многочлена в виде произведения многочленов.

Для разложения многочленов на множители применяют вынесение общего множителя за скобки, группировку, формулы сокращённого умножения. Например, многочлен 5х 3 – х 2 у можно разложить на множители, вынеся за скобки х 2 :

Многочлен 3х – 3у – ах + ау можно разложить на множители, используя способ группировки:

3х – 3у – ах + ау = (3x – 3у) – (ах – ау) = 3(х – у) – а (х – у) = (х – у)(3 – а).

Многочлен а 4 – 25x 2 можно разложить на множители, используя формулу разности квадратов двух выражений:

а 4 – 25x 2 = (а 2 ) 2 – (5x) 2 = (а 2 – 5x)(а 2 + 5x).

Иногда многочлен удаётся разложить на множители, применив последовательно несколько способов.

Алгебра 7 класс Все формулы

Уравнения

Решить уравнение с одной переменной — значит найти все его корни или доказать, что корней нет.

☑ 9. Уравнения с одной переменной, имеющие одни и те же корни, называют равносильными. Например, уравнения x 2 = 25 и (х + 5)(х – 5) = 0 равносильны. Каждое из них имеет два корня: –5 и 5. Уравнения, не имеющие корней, также считают равносильными.

При решении уравнений с одной переменной используются следующие свойства:

Если а = 0 и b ≠ 0, то уравнение ах = b не имеет корней. Например, уравнение 0 • х = 7 не имеет корней.

Если а = 0 и b = 0, то корнем уравнения ах = b является любое число.

Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения с двумя переменными, не имеющие решений, также считают равносильными.

В уравнении с двумя переменными можно переносить слагаемые из одной части в другую, изменяя их знаки, и обе части уравнения можно умножать или делить на одно и то же число, не равное нулю. При этом получаются уравнения, равносильные исходному.

☑ 12. Линейным уравнением с двумя переменными называют уравнение вида ах + by = с, где х и у — переменные, а, b и с — числа.

☑ 13. Графиком уравнения с двумя переменными называют множество точек координатной плоскости, координаты которых являются решениями этого уравнения.

Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.

☑ 14. Решением системы уравнений с двумя переменными называют пару значений переменных, обращающую каждое уравнение системы в верное равенство. Например, пара чисел х = 7, у = –1 — решение системы
так как является верным каждое из равенств 7 + (–1) = 6 и 2 • 7 – (–1) = 15.

Решить систему уравнений — значит найти все её решения или доказать, что решений нет.

Системы уравнений с двумя переменными, имеющие одни и те же решения, называют равносильными. Системы, не имеющие решений, также считают равносильными.

☑ 15. Для решения систем линейных уравнений с двумя переменными используются графический способ, способ подстановки, способ сложения.

При графическом способе строят графики линейных уравнений (прямые) и анализируют их расположение:

При решении системы двух линейных уравнений с двумя переменными способом подстановки поступают следующим образом:

При решении системы двух линейных уравнений с двумя переменными способом сложения поступают следующим образом:

Алгебра 7 класс Все формулы

Функции

Независимую переменную иначе называют аргументом, а о зависимой переменной говорят, что она является функцией этого аргумента. Все значения, которые принимает независимая переменная, образуют область определения функции.

Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

Графиком линейной функции у = kx + b является прямая. Число k называют угловым коэффициентом прямой, являющейся графиком функции у = kx + b.

Графики двух линейных функций пересекаются, если их угловые коэффициенты различны, и параллельны, если их угловые коэффициенты одинаковы.

Линейную функцию, задаваемую формулой у = kx при k ≠ 0, называют прямой пропорциональностью.

График прямой пропорциональности есть прямая, проходящая через начало координат. При k > 0 график расположен в первой и третьей координатных четвертях, а при k у = х 2 — парабола. Этот график проходит через начало координат и расположен в первой и второй координатных четвертях. Он симметричен относительно оси у.

График функции у = х 3 проходит через начало координат и расположен в первой и третьей координатных четвертях. Он симметричен относительно начала координат.

Статистические характеристики

☑ Средним арифметическим ряда чисел называют частное от деления суммы этих чисел на число слагаемых.

Модой ряда чисел называют число, которое встречается в данном ряду чаще других. Ряд чисел может иметь более одной моды или не иметь моды совсем.

Медианой упорядоченного ряда чисел с нечётным числом членов называют число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называют среднее арифметическое двух чисел, записанных посередине.

Например, медиана ряда чисел 17, 21, 27, 29, 32, 37, 41 равна 29, а медиана ряда чисел 28, 43, 54, 56, 58, 62 равна 55.

Медианой произвольного ряда чисел называют медиану соответствующего упорядоченного ряда.

Размахом ряда чисел называют разность между наибольшим и наименьшим из этих чисел.

Вы смотрели Конспект «Алгебра 7 класс Все формулы и определения» — краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского). Выберите дальнейшие действия:

Источник

Правила по алгебре 7 класс

Выражение с переменными

— это выражение, состоящее из чисел.

— это выражение, состоящее из чисел и переменных (букв)

Уравнение вида где  переменная,  некоторые числа, называют линейным уравнением с одной переменной.

Математическая модель – составленное по данному условию уравнение.

Алгоритм – последовательность действий.

Выражения, соответственные значения которых равны при любых значениях, входящих в них переменных, называют тождественно равными.

Равенство, верное при любых значениях входящих в него переменных, называют тождеством.

Степень числа а с показателем 1 называют само это число.

При возведении отрицательного числа в степень с чётным показателем получаем положительное число. При возведении отрицательного числа в степень с нечётным показателем получаем отрицательного числа.

Одночлен – произведение чисел, переменных и их степеней.

Коэффициент одночлена – числовой множитель одночлена, записанного в стандартном виде.

Подобные одночлены – одночлены, имеющие одинаковую буквенную часть.

Многочлены – выражения, состоящие из суммы нескольких одночленов.

Многочлен стандартного вида – многочлен, состоящий из одночленов стандартного вида.

Степень многочлена стандартного вида – наибольшая степень из степени одночлена, из которых составлен многочлен.

Нуль – многочлен – число нуль, также многочлены, тождественно равные нулю.

Тождественно равные выражения – выражения, соответственные значения которых равны при любых значениях входящих в них переменных.

Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить.

Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.

Разложение многочлена на множители: представление многочлена в виде произведения нескольких многочленов.

Формулы сокращенного умножения

Полный квадрат – трехчлен, который можно представить в виде квадрата двучлена.

Функция – правило, с помощью которого по каждому значению независимой переменной можно найти единственное значение зависимой переменной.

Функциональная зависимость – зависимость одной переменной от другой.

Область определения – все значения, которые принимает аргумент.

Значение функции – значение зависимой переменной.

Заданная функция – функция, где указаны её область определения и правило, с помощью которого можно по каждому значению независимой переменной найти значение зависимой переменной.

Область значений функций – все значения, которые принимает зависимая переменная.

Способы задание функции: 1. Описательный, 2. С помощью формул, 3. Табличный.

Все точки координатной плоскости, которые можно отметить, действуя таким способом, образуют график функции.

Линейная функция – функция, которую можно задать формулой Её график – прямая.

Линейная функция, которая задается формулой называют прямой пропорциональностью.

Случай, когда значение функции будет оставаться неизменным при любых значениях аргумента.

Равенство, содержащее две переменные называется уравнением с двумя переменными.

Пару значений, обращающую уравнение в верное равенство называют решением уравнения с двумя переменными.

Решить уравнение с двумя переменными – значит найти все его решения или показать, что оно не имеет решений.

График уравнения с двумя переменными – геометрическая фигура, состоящая из всех тех, и только тех точек координатной плоскости, координаты которых (пары чисел) являются решением данного уравнения.

Линейное уравнение с двумя переменными называют уравнение вида

Случай, когда графиком уравнения является прямая.

Решить систему уравнений – значит найти все её решения или показать, что оно не имеет решений.

Суть графического метода: 1) построить на одной координатной плоскости графики уравнений, входящих в систему, 2) найти координаты всех точек пересечения графиков, 3) полученные пары чисел будут искомыми рениями.

Суть метода подстановки: 1) выразить из любого уравнения системы одну переменную через другую, 2) подставить в другое уравнение системы, вместо этой переменной, 3) решить уравнение с одной переменной, 4) подставить найденное значение переменной в выражение, получено на первом шаге, 5) вычислить значение другой переменной.

Суть метода сложения: 1) подобрав «выгодные» множители, преобразовать одно или оба уравнения системы так, чтобы коэффициентом при одной из переменных стали противоположными числами, 2) сложить почленно левые и правые части уравнений, 3) решить уравнение с одной переменной, 4)подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы, 5) вычислить значение другой переменной.

Источник