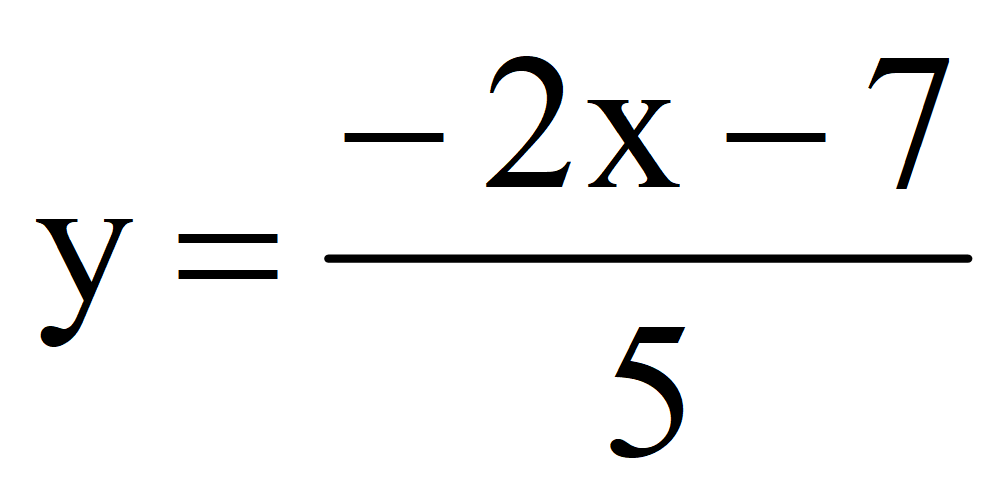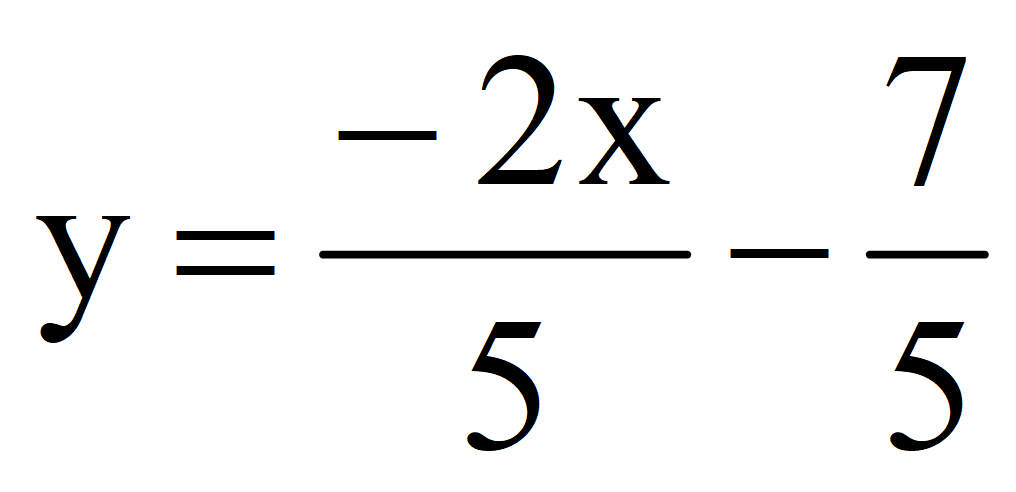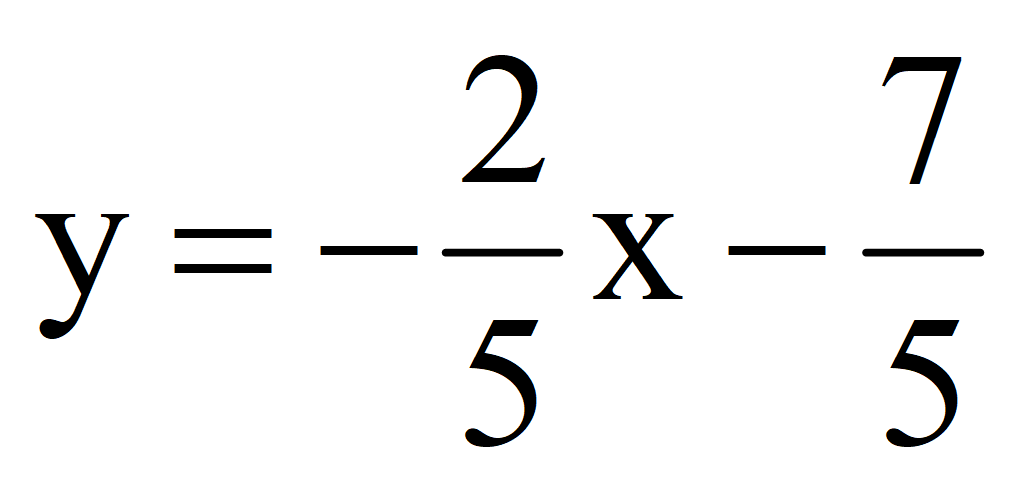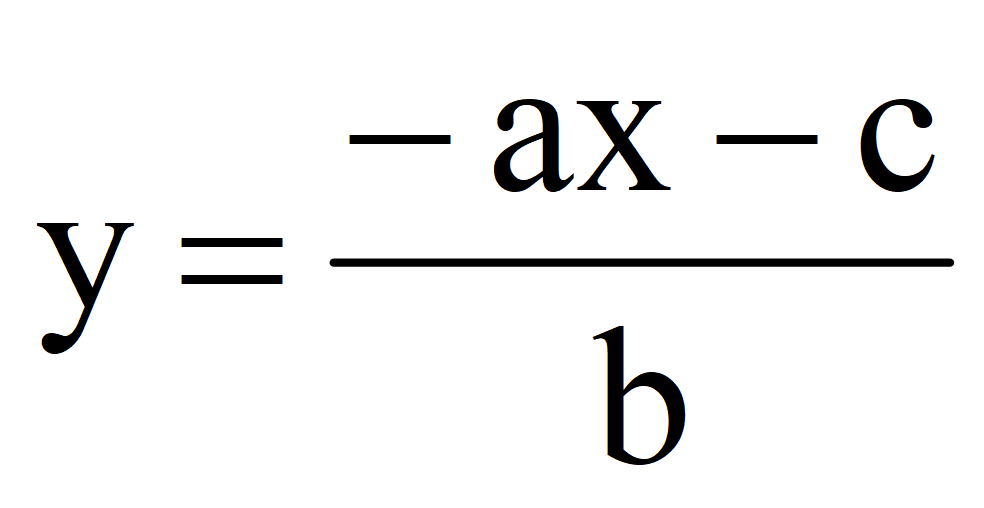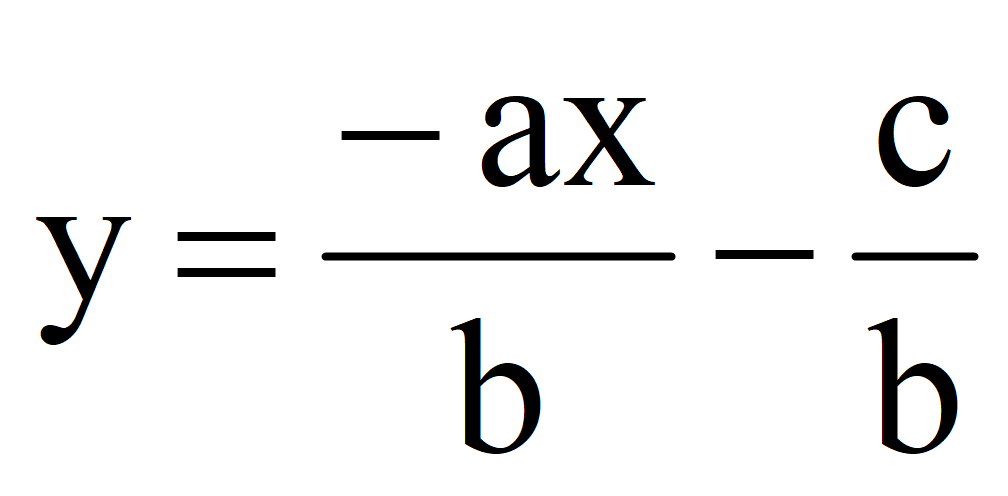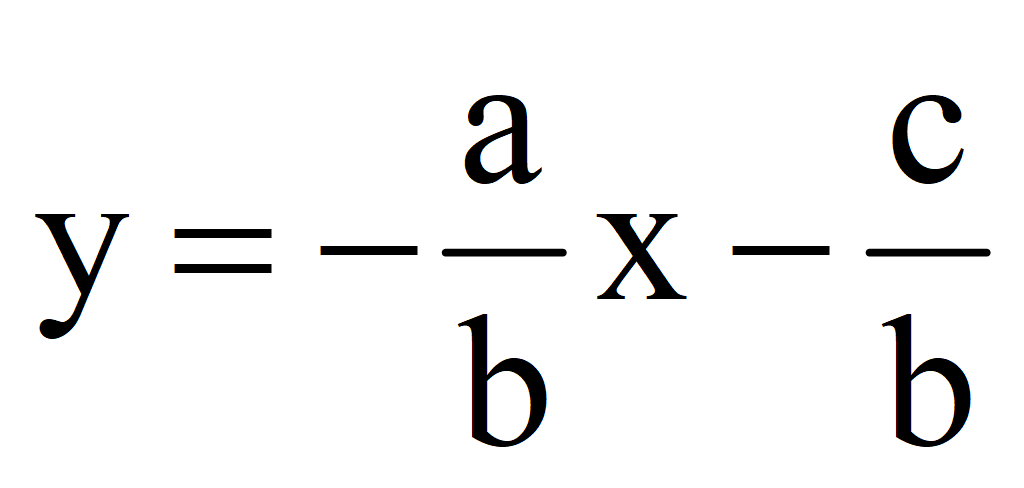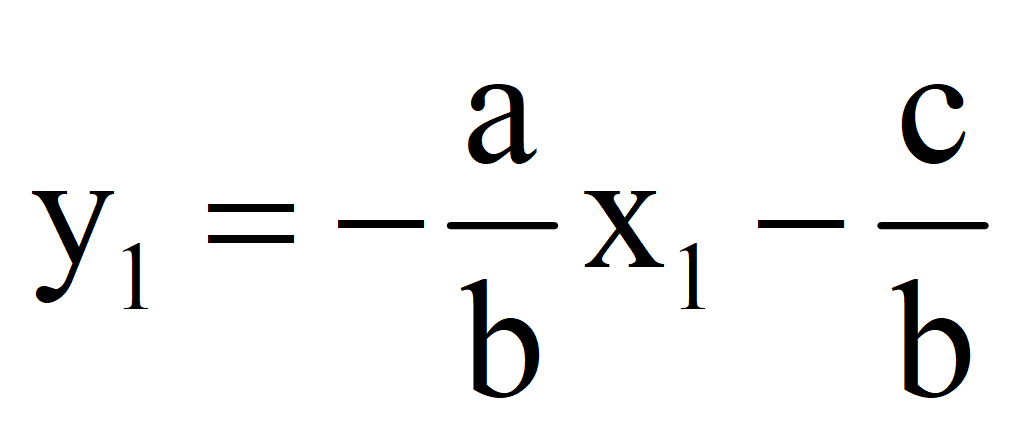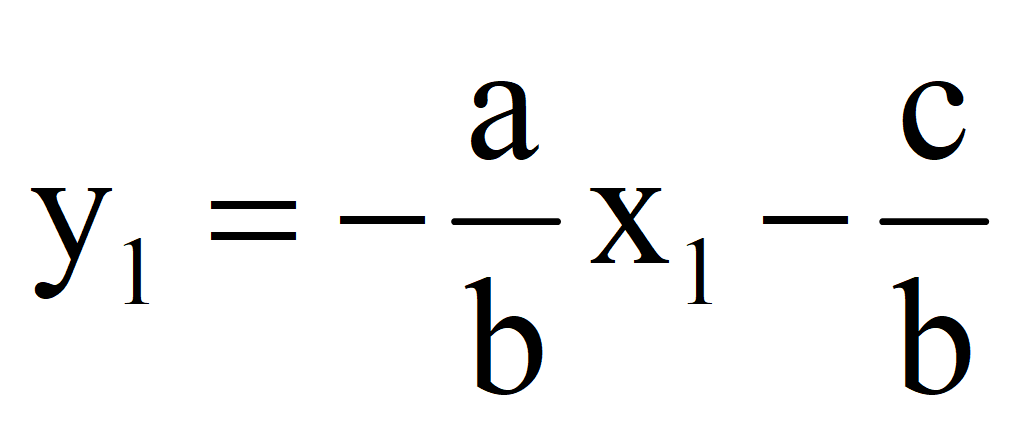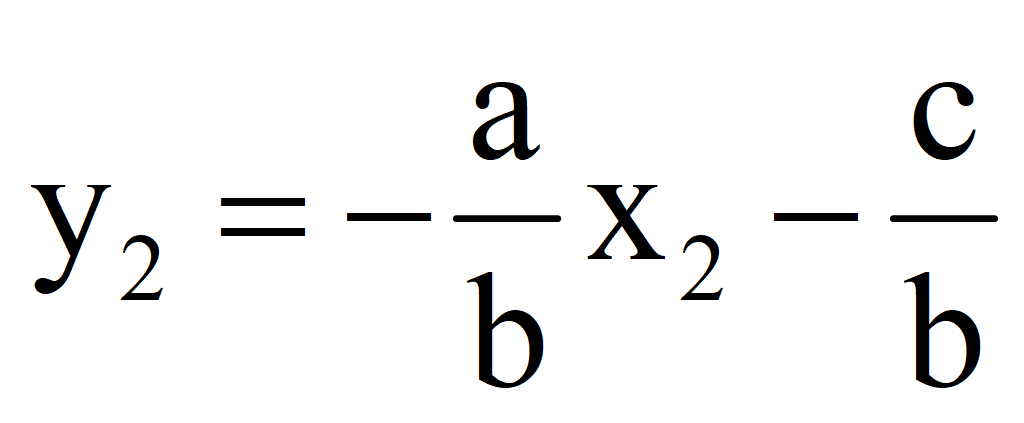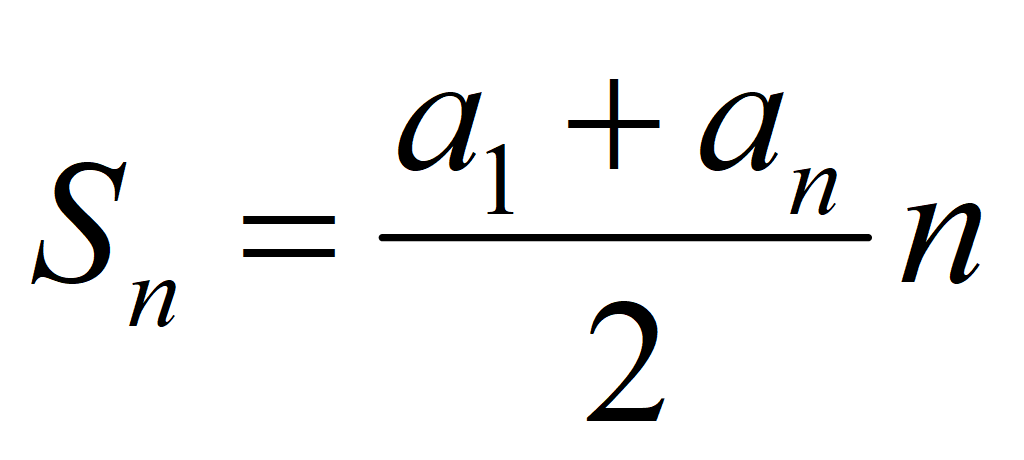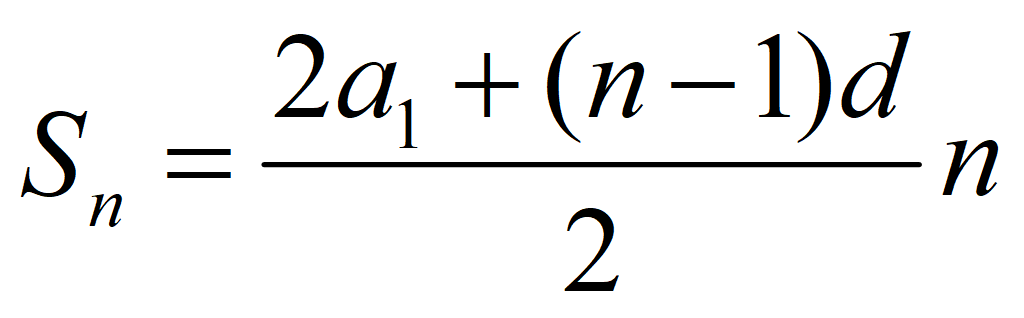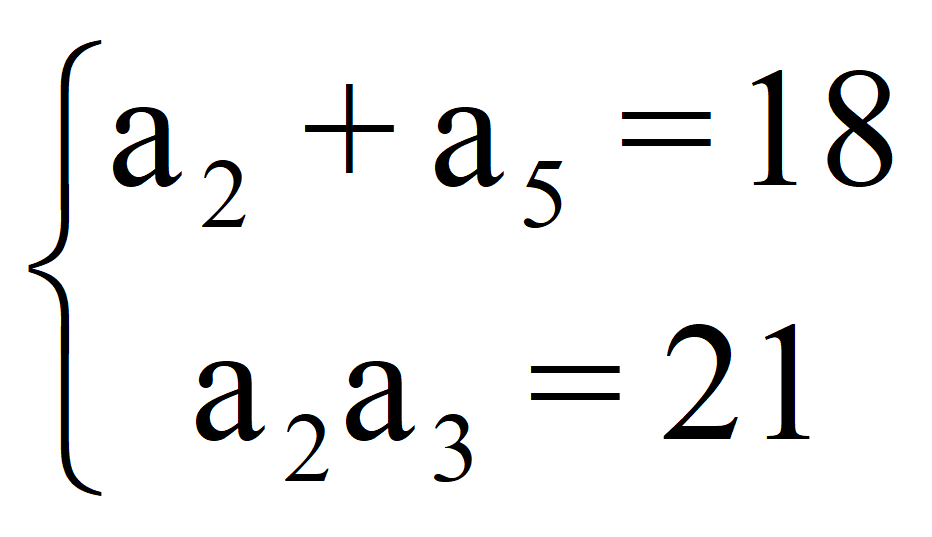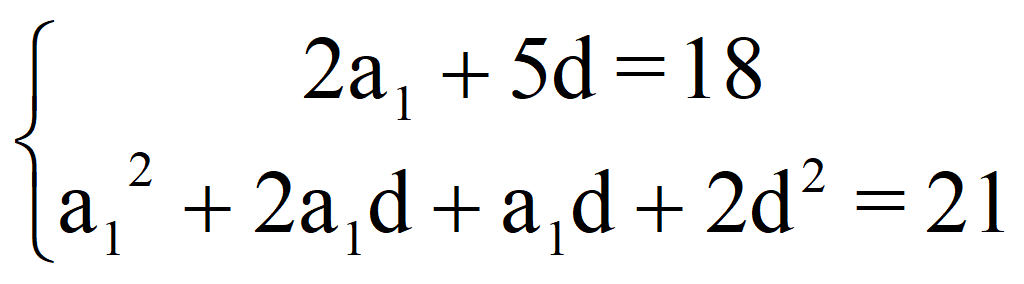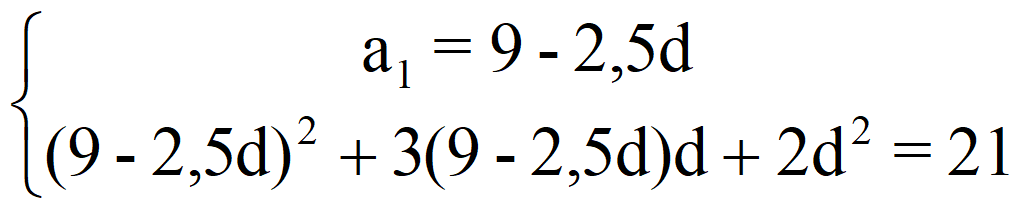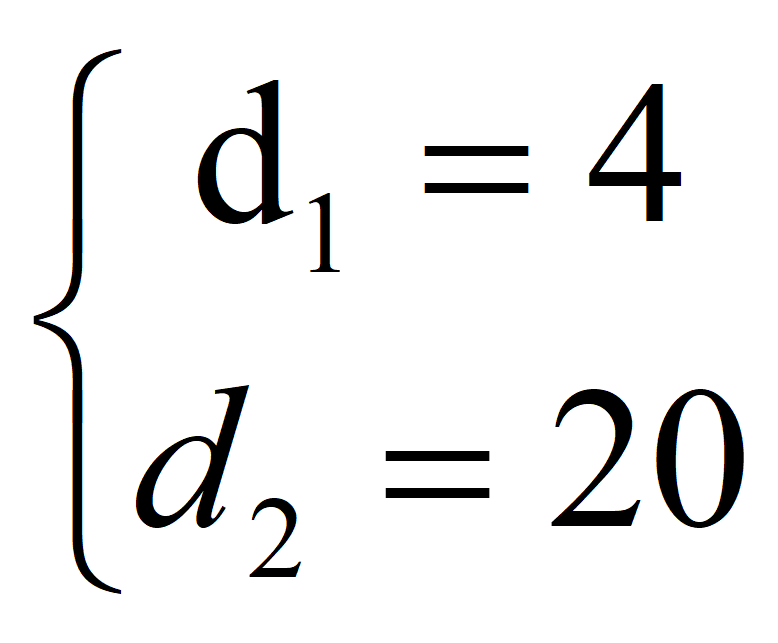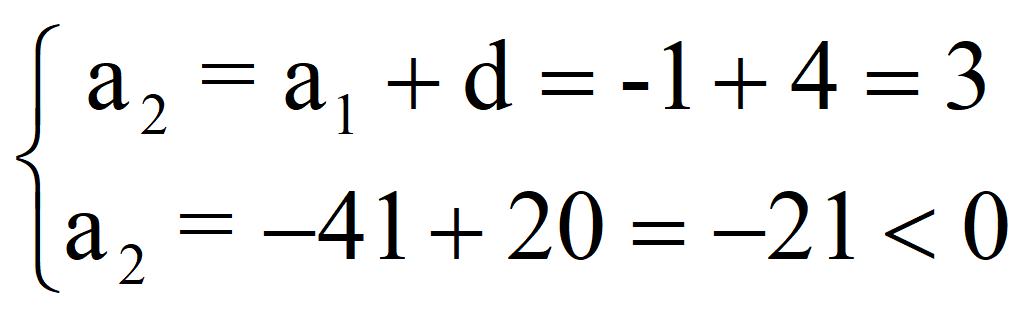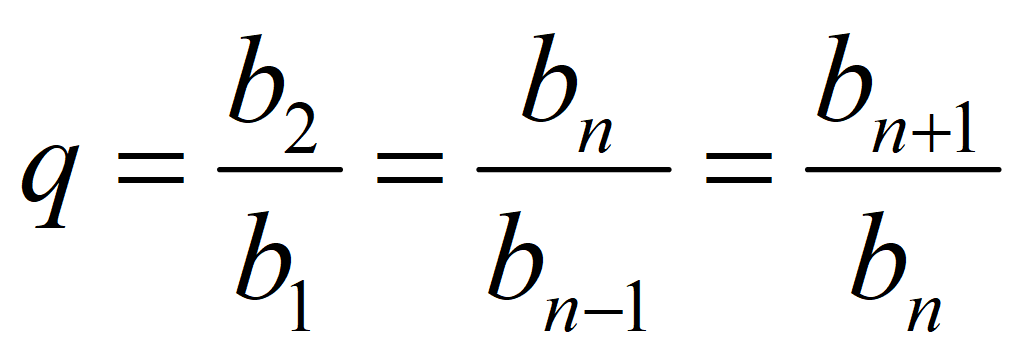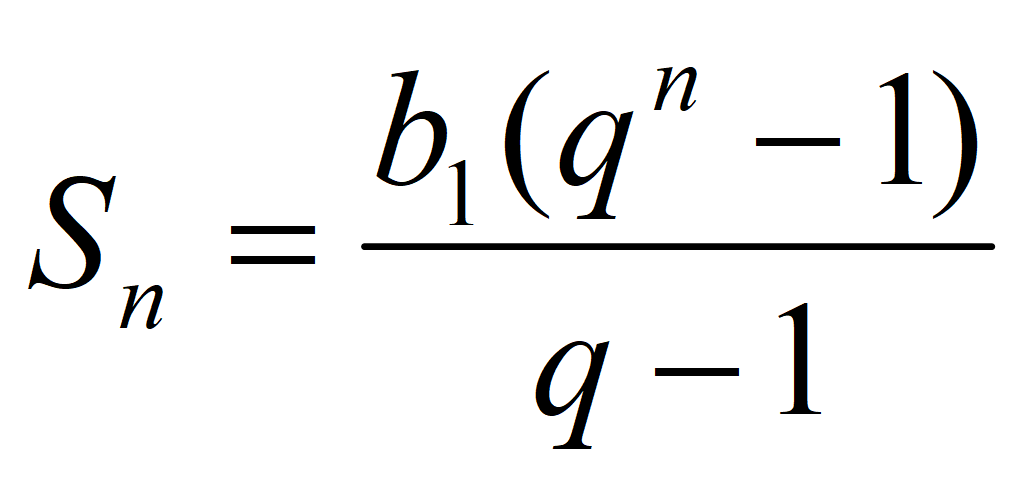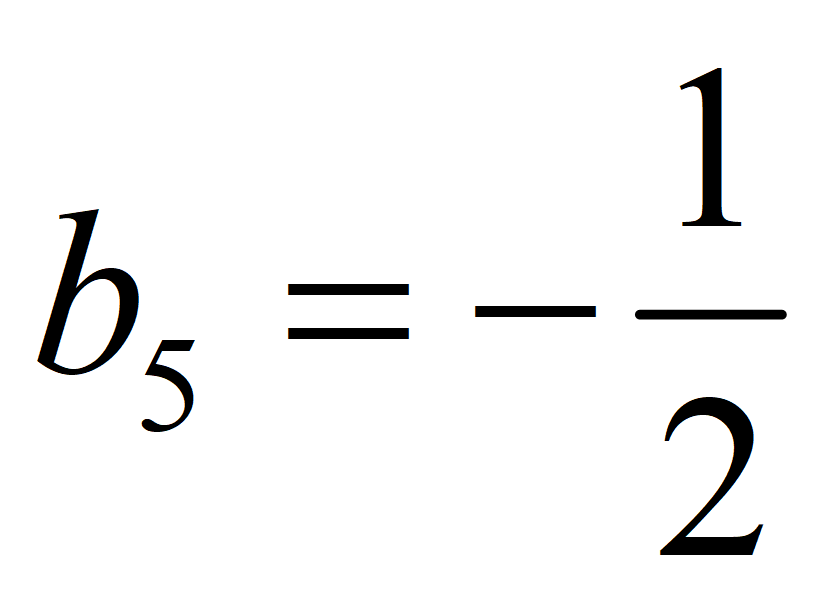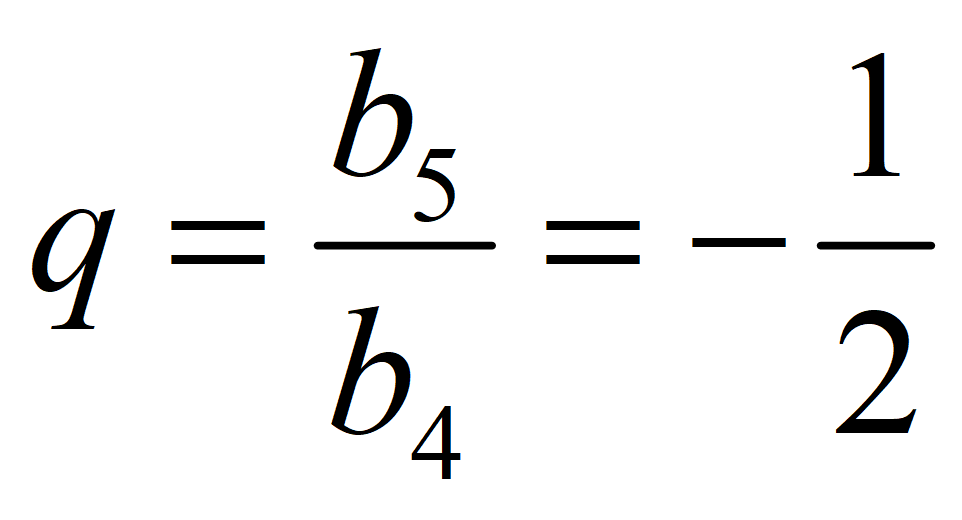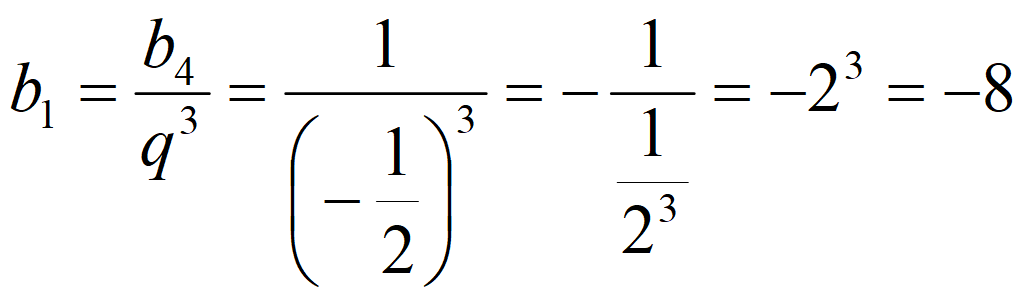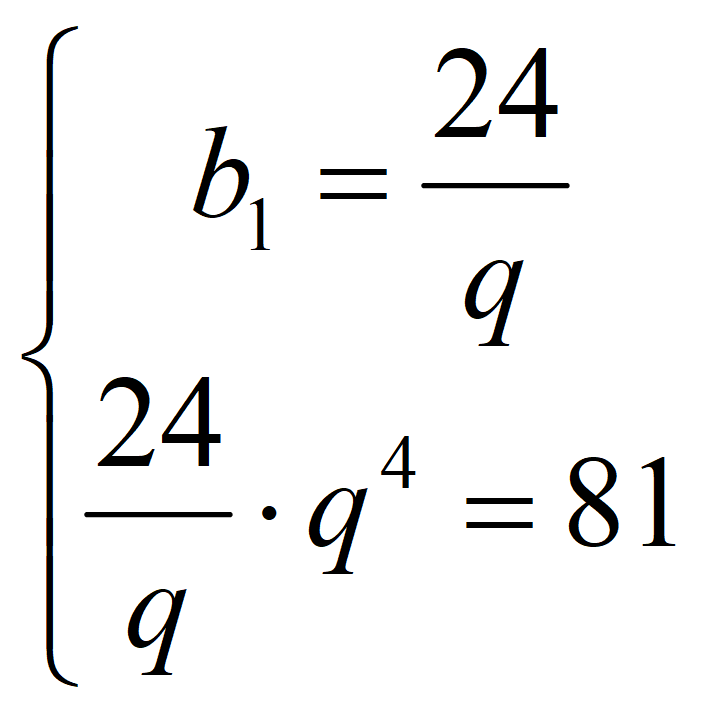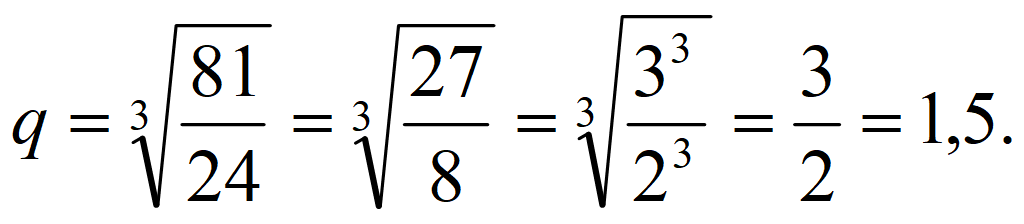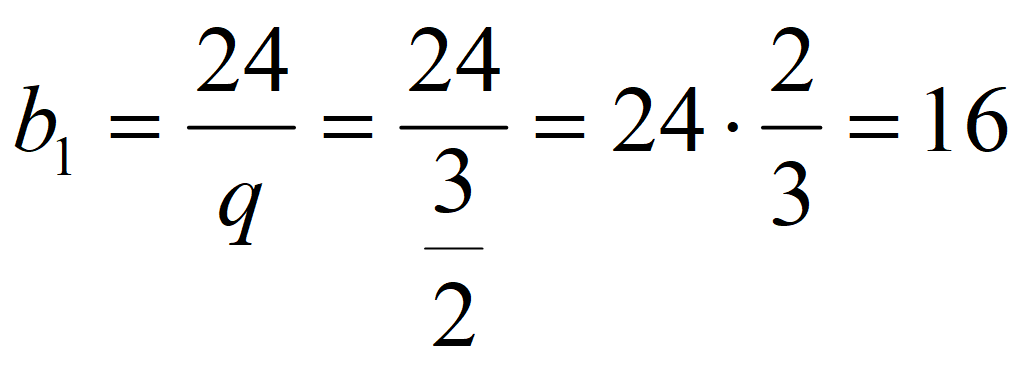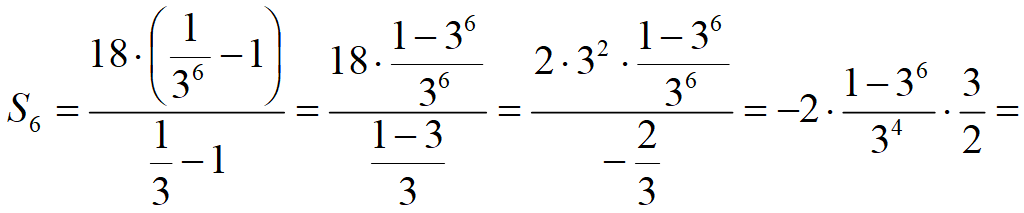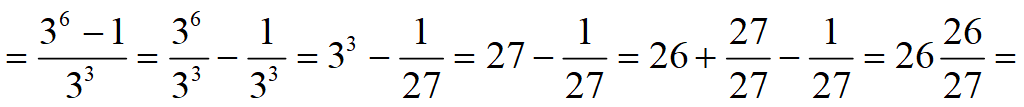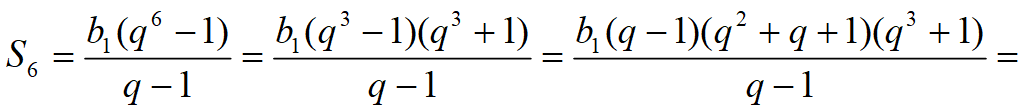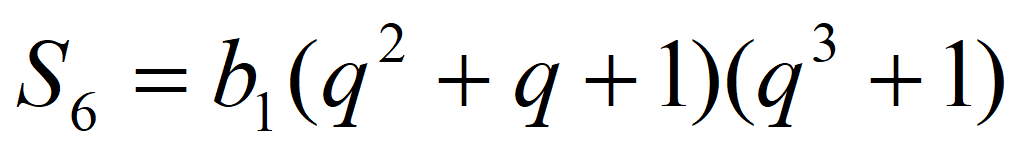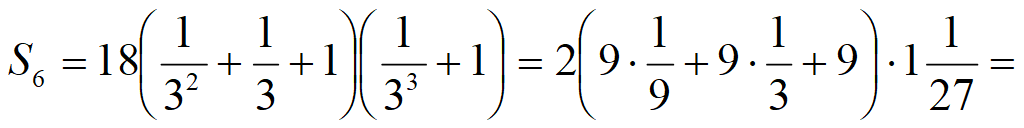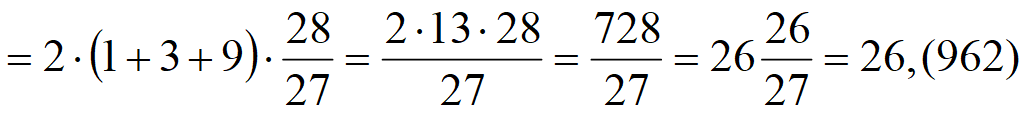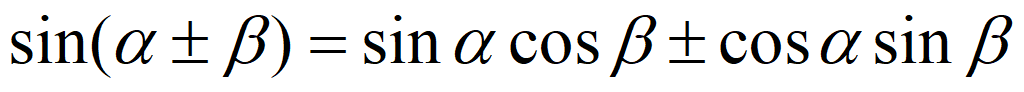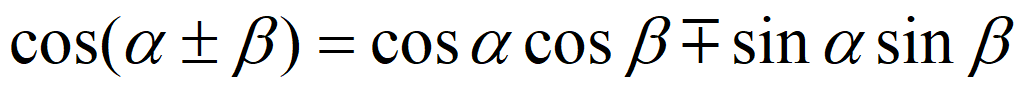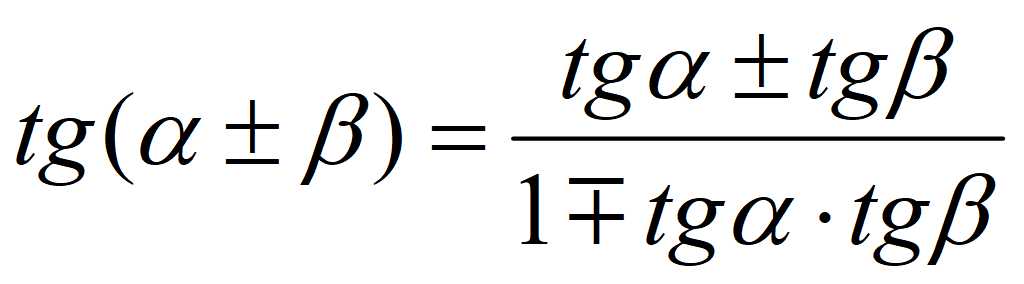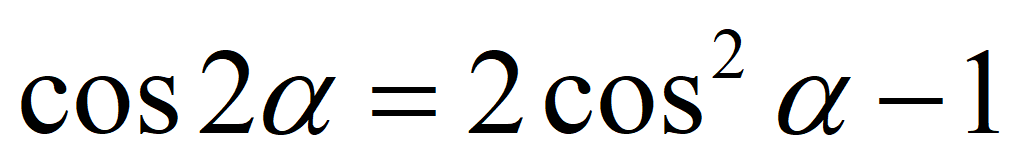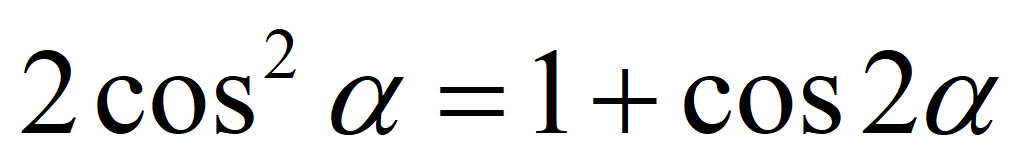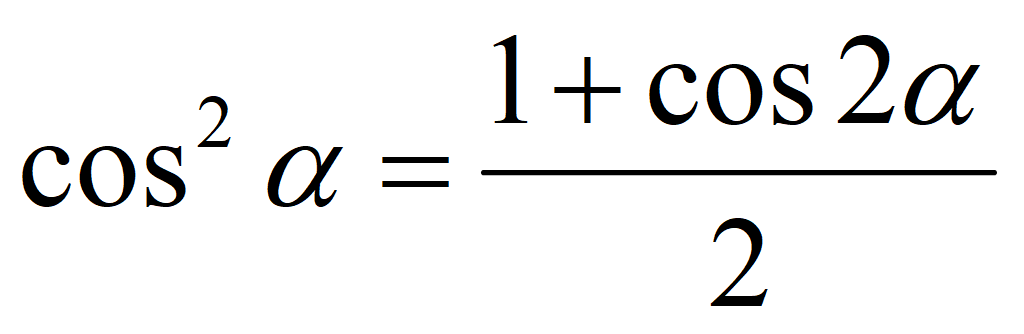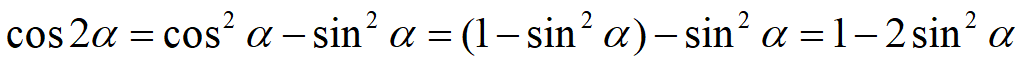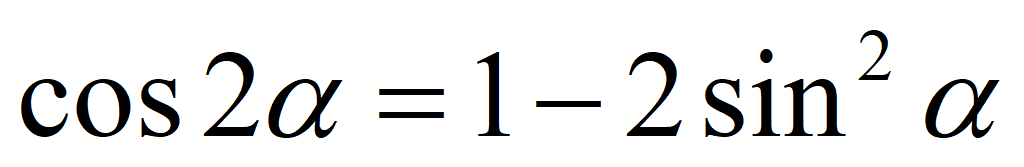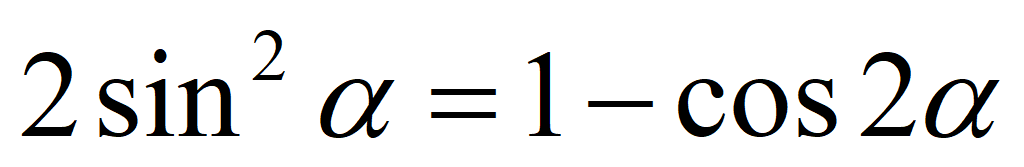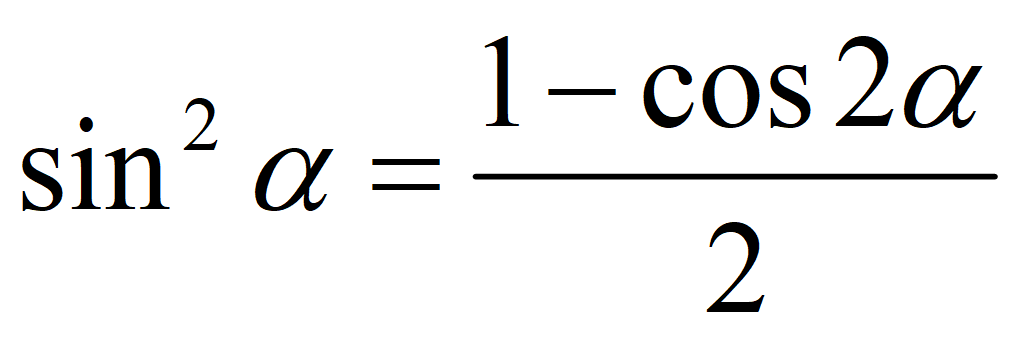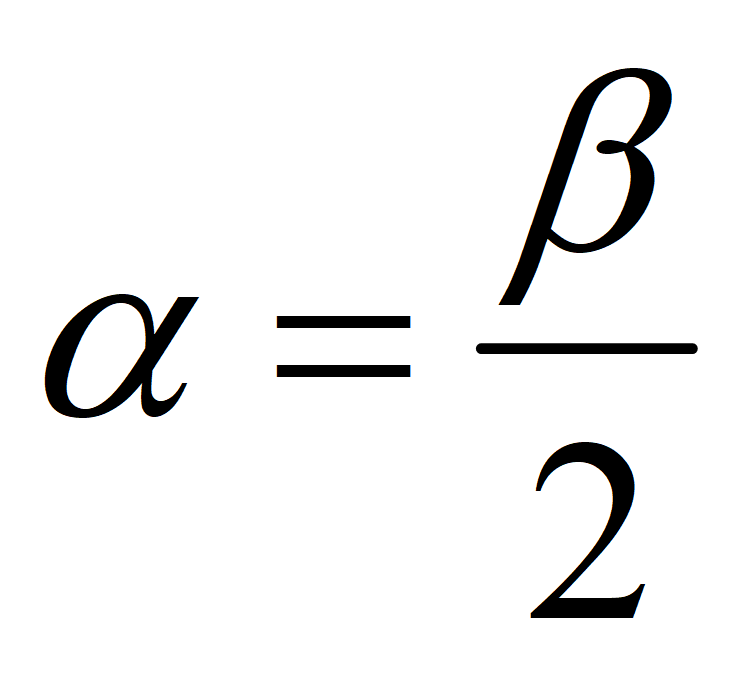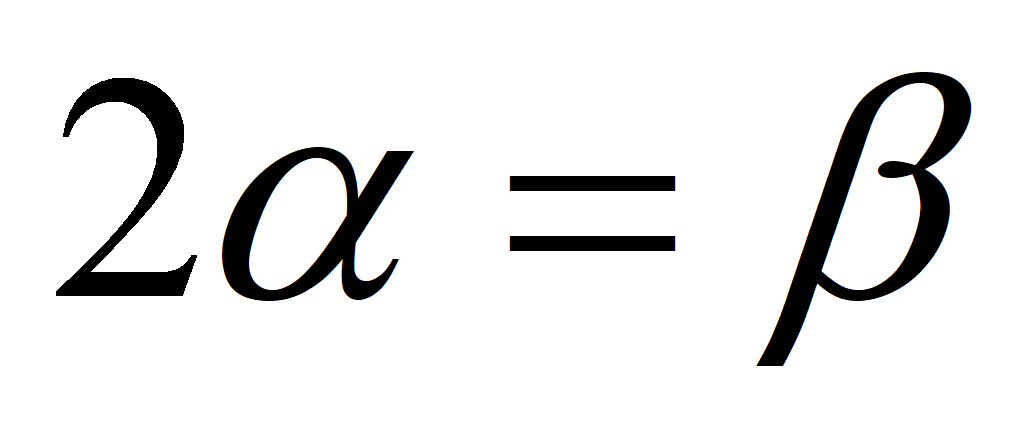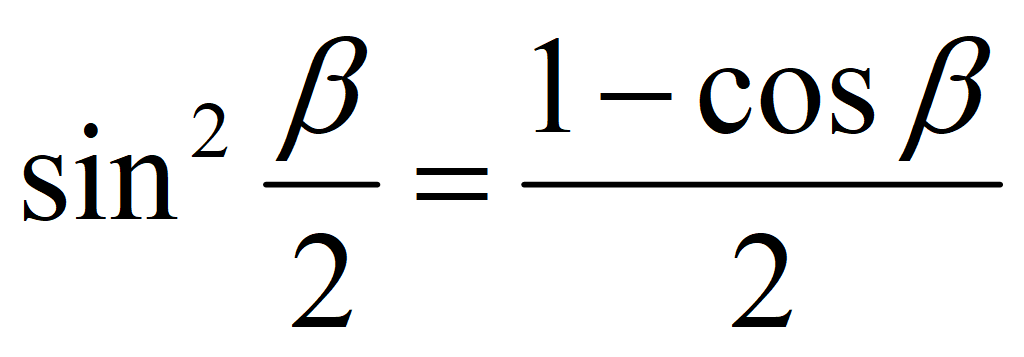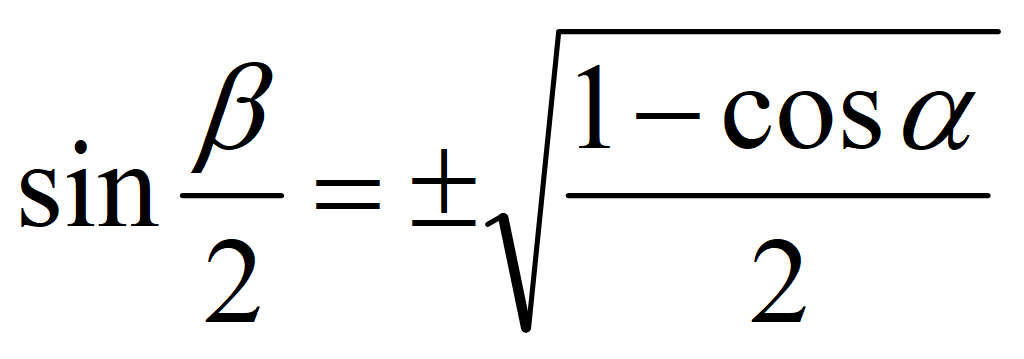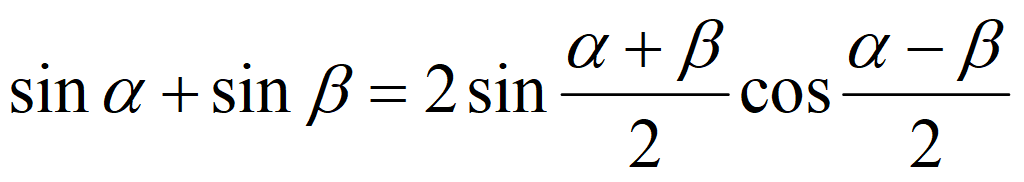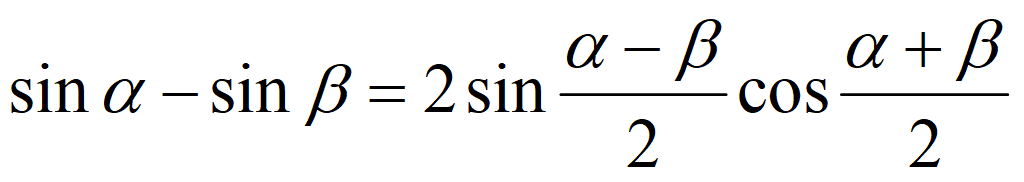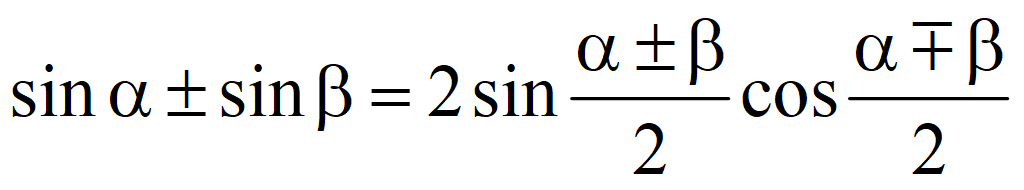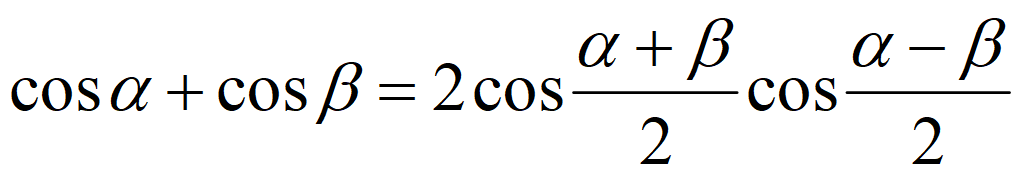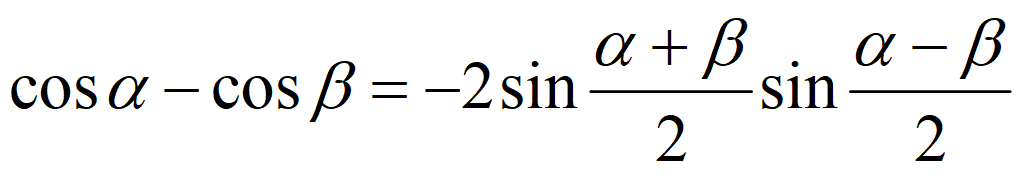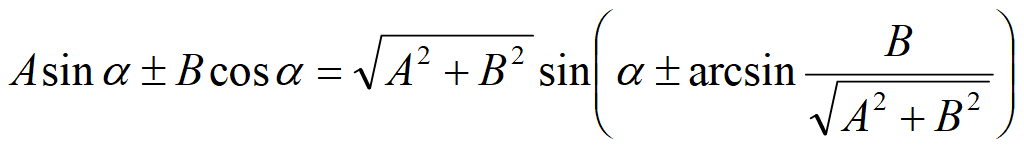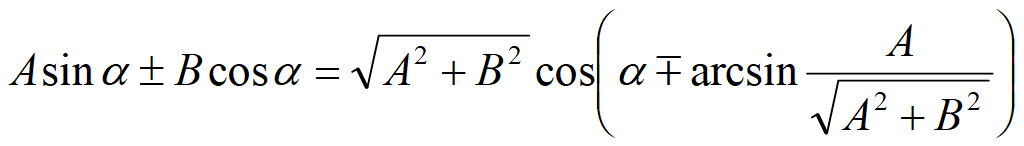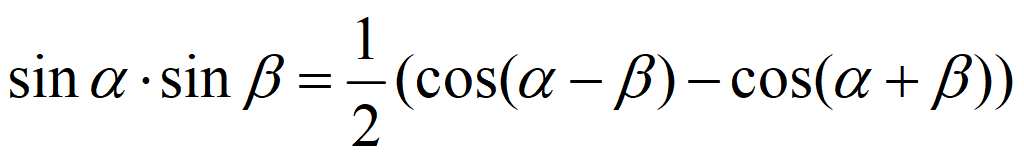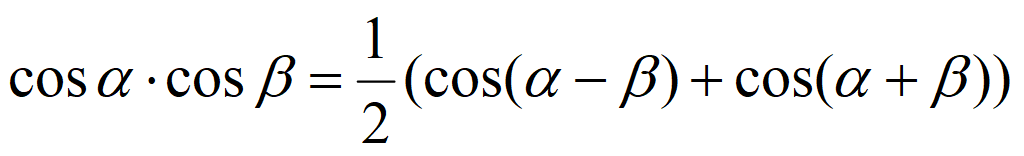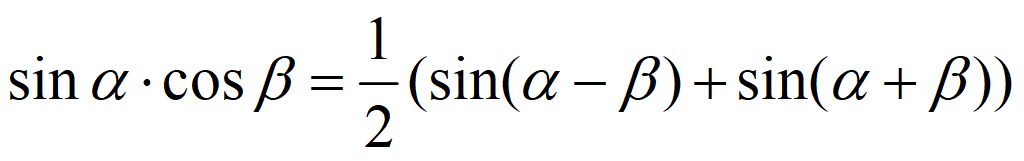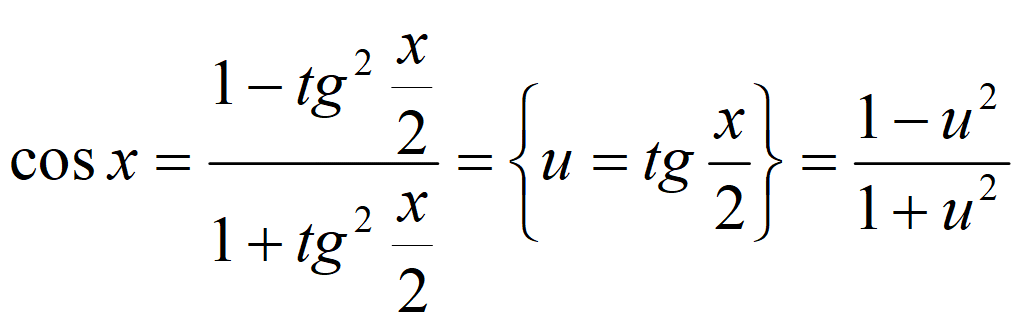что нужно знать для 7 класса по математике

Алгебра и геометрия в 7 классе, как всё знать

Что делать, если ребенок не понимает алгебру и геометрию в седьмом классе? Как решебники и ГДЗ способны заменить репетитора.

Реально ли выучить алгебру и геометрию в 7 классе без репетитора

Каждый учащийся постоянно слышит о том, что повторять пройденный материал необходимо систематически. Но по разным причинам это не всегда получается. И наступает момент, когда совершенно непонятно, что происходит на уроках алгебры и геометрии. Эти предметы имеют характерную черту – новые темы обязательно опираются на предыдущие. И достаточно одного пропуска, чтобы непонимание, как лавина, потянуло за собой неуспеваемость.

Чтобы подтянуть знания чаще всего рекомендуются занятия с репетитором. Но этот вариант не всем подходит. Неужели нереально выучить алгебру и геометрию самостоятельно? Нет ничего не возможного, когда под рукой решебник по алгебре для 7 класса под редакцией Макарычева. Также на помощь приходят ГДЗ, главное уметь правильно ими пользоваться.

Изучаем алгебру без слез

Это один из самых сложных предметов, изложенный сухим языком с массой формул и правил. Здесь мало просто вызубрить, материал необходимо понять. Особое внимание необходимо уделить решению практических задач, ответы на которые красноречиво указывают, есть ли пробелы в знаниях. Важно не торопиться и постепенно переходить от простого к сложному. Если какая-то тема осталась непонятой, ее необходимо разобрать самостоятельно. Поможет в этом решебник под редакцией Макарычева.

Этот учебник отличное пособие для самопроверки, так как в нем можно найти все подсказки. Материал изложен максимально доступно, что позволяет семиклассникам понять тему, даже если урок был пропущен по болезни. Также к решебнику есть ГДЗ, где все задания уже решены и имеют обязательные разъяснения по ходу выполнения работы. В процессе изучения можно обнаружить непонятные для себя выражения, их нельзя оставлять без внимания. Если вникнуть в слово или предложение самостоятельно не получилось, необходимо задать вопрос учителю на уроке и попросить их объяснить.

Готовые домашние задания по геометрии в помощь родителям

Редко кто из родителей может самостоятельно вспомнить и решить упражнения практикума по геометрии в седьмом классе. Им в помощь были создано ГДЗ по геометрии 7-9 класс Атанасяна Л.С. Пособие включает в себя четыре объемных главы, где собраны все рассматриваемые в школе темы. С помощью учебника можно изучить:

Отдельный раздел в решебнике отведен разбору задач повышенной сложности и примерам на повторение пройденного материала. Детальный алгоритм решения позволит не только подготовиться к следующему уроку семиклассникам, но и восполнить пробелы в знаниях всем тем, кто готовится к ЕГЭ.

Особенно удобно то, что оба этих учебника можно найти онлайн на сыйте gdzplus. Просмотреть нужную информацию можно просто воспользовавшись смартфоном или любым другим подходящим гаджетом. Пошаговые алгоритмы, разобранные в решебниках позволят сэкономить на найме репетитора и убрать пробелы в знаниях.

Источник

Краткий курс алгебра 7 класс

Краткий курс в определениях и формулах 7 класс.Удобно для повторения и подготовки к экзаменам.

Просмотр содержимого документа
«Краткий курс алгебра 7 класс»

Числовые и буквенные выражения.

Решение задачи разбивается на 3 этапа а). Составление математической модели; б). Работа с математической моделью; в).Ответ на вопрос задачи.

Существует несколько видов моделей: Словесная модель(реальные ситуации описываются словами), алгебраическая модель (алгебраически ), геометрическая модель ( в геометрии и графики).

Линейные уравнения с одним неизвестным.

Алгоритм решения линейного уравнения ах+б=0 в случае когда а ≠ 0.

Алгоритм решения линейного уравнения ах+б=сх+д (а≠ с )

Перенести все члены уравнения из правой части в левую с противоположными знаками.

Получится уравнение вида кх+м=0.

называют координатной прямой или координатной осью.

Алгоритм отыскания координат точки М, заданной в системе координат хОу.

Алгоритм построения точки М(а;б) в прямоугольной системе координат хОу.

Построить прямую у=б.

Найти точку пересечения построенных прямых – это и будет точка М(а;б).

Линейное уравнение с двумя переменными.

Графиком линейного уравнения является прямая.

Придать переменной х конкретное значение х=х₁ ( х=0 ) найти из уравнения ах₁+бу+с=0 соответствующее значение у=у₁.

Придать переменной у конкретное значение у=у₂ ( у=0 ) найти из уравнения ах+бу₂+с=0 соответствующее значение х=х₂.

Построить на координатной плоскости хОу точки (х₁;у₁) и (х₂;у₂).

Провести через эти две точки прямую – она и будет графиком уравнения ах+бу+с=0.

У линейной функции х- независимая переменная ( или аргумент ), у – зависимая переменная ( или функция ).

Теорема 2. Графиком линейной функции у= кх +м является прямая.

Если к › 0 то функция у=кх + м возрастает.

Если к ‹ 0 то функция у=кх + м убывает.

Коэффициент К в записи у=кх называют угловым коэффициентом.

Системы двух линейных уравнений с двумя переменными.

Пару значений (х;у), которая одновременно является решением и первого и второго уравнений системы, называют решением системы.

Графический метод решения системы.

Если прямые совпадают, то система имеет бесконечное множество решений ( система неопределенна)

Алгоритм решения системы двух уравнений с двумя переменными методом подстановки.

Выразить У через Х из первого уравнения системы.

Подставить полученное на первом шаге выражение вместо У во второе уравнение системы.

Решить полученное на втором шаге уравнение относительно Х.

Метод алгебраического сложения.

Степень с натуральным показателем.

Степенью числа а с показателем 1 называют само это число.

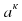
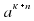
Теорема 1. Для любого числа а и любых натуральных чисел n и к справедливо равенство *=( При умножении степеней с одинаковыми основаниями показатели складываются)

Теорема 3. Для любого числа а и любых натуральных чисел n и к справедливо равенство = ( При возведении степи в степень показатели умножаются).

Если а ≠ 0, то 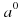= 1.

Чтобы привести одночлен к стандартному виду, нужно: а) перемножить все числовые множители и поставить их произведение на первое место; б) перемножить все имеющиеся степени с одним буквенным основанием; в) перемножить все имеющиеся степени с другим буквенным основанием и т.д.

Алгоритм сложения одночленов.

Привести все одночлены к стандартному виду.

Найти сумму коэффициентов подобных одночленов.

Многочлены. Арифметические операции над многочленами.

Многочленом называют сумму одночленов.

Чтобы записать алгебраическую сумму нескольких многочленов в виде многочлена стандартного вида, нужно раскрыть скобки и привести подобные члены.

Чтобы умножить многочлен на одночлен, нужно каждый член многочлена умножить на этот одночлен и полученные произведения сложить.

Чтобы умножить многочлен на многочлен, нужно умножить каждый член одного многочлена поочерёдно на каждый член другого многочлена и полученные произведения сложить.

Квадрат суммы двух выражений равен сумме их квадратов плюс их удвоенное произведение. =+2аб+

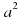
Квадрат разности двух выражений равен сумме их квадратов минус их удвоенное произведение.=-2аб+

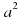
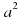
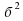
Разность квадратов двух выражений равна произведению суммы этих выражений на их разность. — = (а- б)(а+ б).

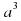
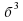
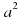
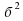
Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы. — = (а- б)(+ аб+).

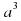
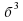
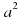
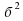
Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности. + = (а + б)(— аб+).

Разложение многочленов на множители.

Способ вынесения общего множителя за скобки.

Сокращение алгебраических дробей.

Функция у = и её график.

Графиком функции у = является парабола.

Источник

Требования к математической подготовке учащихся 7 классов.

КОУ ВО «Школа-интернат №6 для детей с ограниченными возможностями здоровья»

ТРЕБОВАНИЯ К МАТЕМАТИЧЕСКОЙ ПОДГОТОВКЕ УЧАЩИХСЯ.

В результате изучения курса МАТЕМАТИКИ, АЛГЕБРЫ учащиеся должны знать и уметь:

— выполнять арифметические действия с положительными и отрицательными числами;

— уметь сравнивать два числа, упорядочивать в несложных случаях наборы чисел, изображать числа точками на координатной прямой;

— уметь находить значение степени с натуральным показателем и выполнять основные действия со степенями с натуральным показателем. Применять калькулятор;

— уметь округлять целые числа и десятичные дроби;

— уметь правильно употреблять буквенную символику, понимать смысл терминов «выражения», «тождественные преобразования», формулировки заданий: «упростить выражение», «разложить на множители» ;

— уметь составлять несложные буквенные выражения и формулы, осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления /выражать в формулах основных видов одни переменные через другие/;

— уметь выполнять основные действия с многочленами;

— уметь выполнять разложение многочленов на множители вынесением общего множителя за скобки, приводить подобные слагаемые;

— правильно употреблять термины «уравнения», «корень уравнения»; понимать их в тексте, в речи учителя, понимать формулировку задания «решить уравнения»;

— уметь решать линейные уравнения;

— уметь решать несложные текстовые задачи с помощью составления уравнения;

— правильно употреблять функциональную терминологию / значение функции, аргумент, график функции, область определения/ и символику, понимать ее при чтении текста, в речи учителя в формулировке задач;

— уметь находить значения функции, заданных формулой, таблицей, графиком, решать обратную задачу;

В результате изучения курса ГЕОМЕТРИИ учащиеся должны знать и уметь:

— выполнять чертежи по условию задачи;

— уметь вычислять значения геометрических величин, применяя изученные свойства и формулы;

— уметь решать несложные задачи на вычисление, проводить аргументацию в ходе решения задач;

— владеть алгоритмами решения основных задач на построение.

— уметь доказывать теоремы: о свойствах вертикальных и смежных углов, об углах при основании равнобедренного треугольника.

Источник

Правила по алгебре 7 класс

Выражение с переменными

— это выражение, состоящее из чисел.

— это выражение, состоящее из чисел и переменных (букв)

Уравнение вида где  переменная,  некоторые числа, называют линейным уравнением с одной переменной.

Математическая модель – составленное по данному условию уравнение.

Алгоритм – последовательность действий.

Выражения, соответственные значения которых равны при любых значениях, входящих в них переменных, называют тождественно равными.

Равенство, верное при любых значениях входящих в него переменных, называют тождеством.

Степень числа а с показателем 1 называют само это число.

При возведении отрицательного числа в степень с чётным показателем получаем положительное число. При возведении отрицательного числа в степень с нечётным показателем получаем отрицательного числа.

Одночлен – произведение чисел, переменных и их степеней.

Коэффициент одночлена – числовой множитель одночлена, записанного в стандартном виде.

Подобные одночлены – одночлены, имеющие одинаковую буквенную часть.

Многочлены – выражения, состоящие из суммы нескольких одночленов.

Многочлен стандартного вида – многочлен, состоящий из одночленов стандартного вида.

Степень многочлена стандартного вида – наибольшая степень из степени одночлена, из которых составлен многочлен.

Нуль – многочлен – число нуль, также многочлены, тождественно равные нулю.

Тождественно равные выражения – выражения, соответственные значения которых равны при любых значениях входящих в них переменных.

Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить.

Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.

Разложение многочлена на множители: представление многочлена в виде произведения нескольких многочленов.

Формулы сокращенного умножения

Полный квадрат – трехчлен, который можно представить в виде квадрата двучлена.

Функция – правило, с помощью которого по каждому значению независимой переменной можно найти единственное значение зависимой переменной.

Функциональная зависимость – зависимость одной переменной от другой.

Область определения – все значения, которые принимает аргумент.

Значение функции – значение зависимой переменной.

Заданная функция – функция, где указаны её область определения и правило, с помощью которого можно по каждому значению независимой переменной найти значение зависимой переменной.

Область значений функций – все значения, которые принимает зависимая переменная.

Способы задание функции: 1. Описательный, 2. С помощью формул, 3. Табличный.

Все точки координатной плоскости, которые можно отметить, действуя таким способом, образуют график функции.

Линейная функция – функция, которую можно задать формулой Её график – прямая.

Линейная функция, которая задается формулой называют прямой пропорциональностью.

Случай, когда значение функции будет оставаться неизменным при любых значениях аргумента.

Равенство, содержащее две переменные называется уравнением с двумя переменными.

Пару значений, обращающую уравнение в верное равенство называют решением уравнения с двумя переменными.

Решить уравнение с двумя переменными – значит найти все его решения или показать, что оно не имеет решений.

График уравнения с двумя переменными – геометрическая фигура, состоящая из всех тех, и только тех точек координатной плоскости, координаты которых (пары чисел) являются решением данного уравнения.

Линейное уравнение с двумя переменными называют уравнение вида

Случай, когда графиком уравнения является прямая.

Решить систему уравнений – значит найти все её решения или показать, что оно не имеет решений.

Суть графического метода: 1) построить на одной координатной плоскости графики уравнений, входящих в систему, 2) найти координаты всех точек пересечения графиков, 3) полученные пары чисел будут искомыми рениями.

Суть метода подстановки: 1) выразить из любого уравнения системы одну переменную через другую, 2) подставить в другое уравнение системы, вместо этой переменной, 3) решить уравнение с одной переменной, 4) подставить найденное значение переменной в выражение, получено на первом шаге, 5) вычислить значение другой переменной.

Суть метода сложения: 1) подобрав «выгодные» множители, преобразовать одно или оба уравнения системы так, чтобы коэффициентом при одной из переменных стали противоположными числами, 2) сложить почленно левые и правые части уравнений, 3) решить уравнение с одной переменной, 4)подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы, 5) вычислить значение другой переменной.

Источник

7 класс

Линейное уравнение с двумя переменными

Решением уравнения с двумя переменными, например ax + by + c = 0, называют пару чисел ( x ; y ), удовлетворяющих этому уравнению, то есть дающих верное числовое равенство при подстановке решения в заданное уравнение.

Задача. Найти два решения уравнения 2 x + 5 y + 7 = 0 и построить график функции

Алгоритм нахождения решения линейного уравнения с двумя переменными ax + by + c =0

1.Выразить переменную y через переменную x

2.Задать конкретное значение переменной x = x ₁; найти значение y = y ₁

Алгоритм построения графика линейного уравнения с двумя переменными ax + by + c =0

1.Выразить переменную y через переменную x

2.Задать конкретное значение переменной x = x ₁; найти значение y = y ₁

3.Задать другое конкретное значение переменной x = x ₂; найти значение y = y ₂

5.Через эти две точки провести прямую, которая и является графиком линейного уравнения ax + by + c = 0.

Выразить переменную y через переменную x

Задача. Построить график функции ax + by + c = 0 при a = 1, b = 1 и c = 1

Это уравнение линейной функции, поэтому для построения графика функции достаточно двух точек

Формулы сокращенного умножения

Сумма кубов a 3 + b 3 = (a + b)(a 2 – ab + b 2 ).

8 класс

9 класс

Числовая функция

Область определения функции

Задание функции y = f ( x ) на области определения X или D ( f )

Область значений функции

Способы задания функции

Основные способы задания фунций:

1.Аналитический – функция y = f ( x ) задается формулой (формулами).

Четные и нечетные функции

Для четной функции f ( x ), x ϵ X выполняется равенство

для нечетной функции f ( x ), x ϵ X выполняется равенство

Область определения D ( f ) четной или нечетной функции y = f ( x ) является симметричным множеством.

Если область определения D ( f ) не является симметричным множеством или условия четности и нечетности функции f ( x ) не выполняются, то функция ни четная, ни нечетная.

Законы сложения

2.Распределительный закон ( a + b ) + c = a + ( b + c ).

2.Сочетательный закон ( ab ) c = a ( bc ).

Числовая последовательность

График числовой последовательности представляет из себя набор точек с натуральным аргументом и значениями функции, вычисленными в этих точках.

Аналитический способ задания числовой последовательности

Словесный способ задания последовательности

При словесном способе правило составления последовательности описывается словами, а не формулой.

Рекуррентный способ задания последовательности

Например, последовательность y ₁ = 2; y _n = y _{n -1} + 3, при n > 1 задана рекуррентно.

Арифметическая прогрессия

Арифметическая прогрессия задается рекуррентно:

где первый член a ₁ и разность арифметической прогрессии d – заданны числами;

a _n – член прогрессии, начиная со второго;

a _{n -1} – предыдущий член арифметической прогрессии.

n – ный член арифметической прогрессии

Сумма n членов арифметической прогрессии:

Подставим a _n = a ₁ + (n – 1)d

Подставляем в заданную систему

и получаем систему уравнений

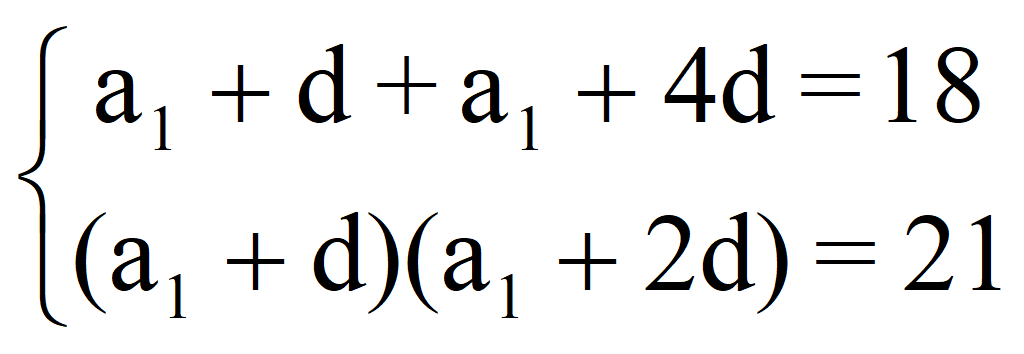
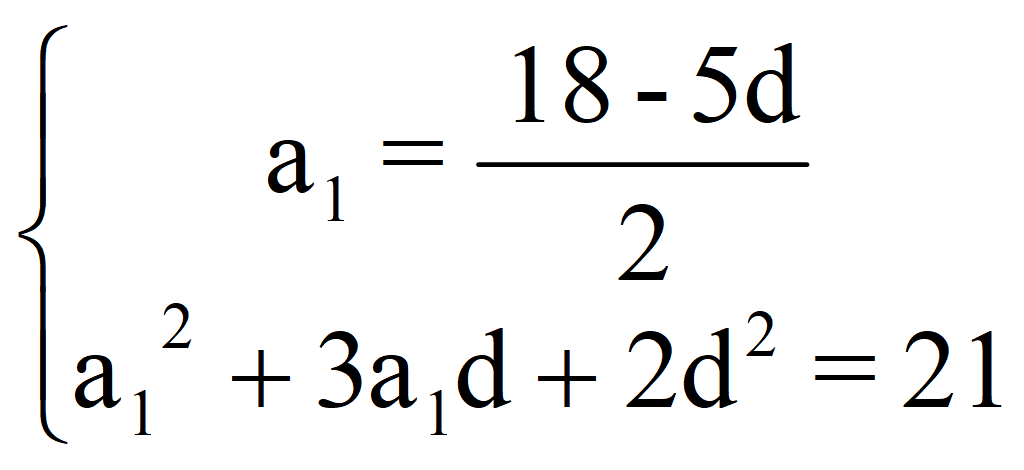
81 – 45 d + 6,25 d 2 + 27 d – 7,5 d 2 + 2 d 2 = 21;

0,75 d 2 – 18 d + 81 – 21 = 0;

0,75 d 2 – 18 d + 60 = 0.

Разделим на 0,75, то есть умножим на 4/3

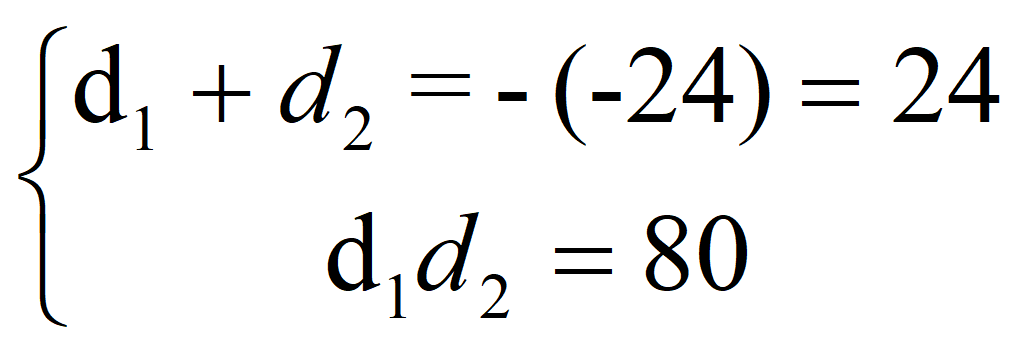
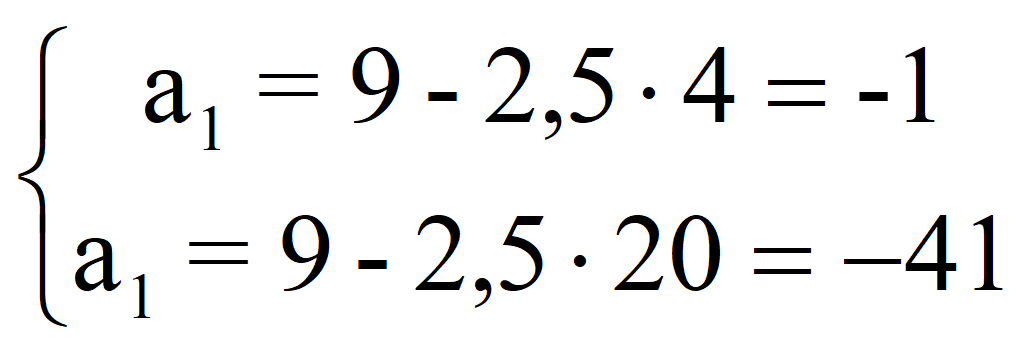
Геометрическая прогрессия

Геометрическая прогрессия задается рекуррентно:

где первый член b ₁ и знаменатель геометрической прогрессии q – заданны числами;

b _n – член прогрессии, начиная со второго;

b _{n -1} – предыдущий член арифметической прогрессии.

Знаменатель геометрической прогрессии

Задача 17.12 (б) [Мордкович. Задачник 9 класс]

Найдите b ₁ и q для геометрической прогрессии ( b _n ), заданной следующими условиями:

b ₄ = 1,

Знаменатель геометрической прогрессии

Формула 4-го члена геометрической прогрессии:

Задача 17.22 (б) [Мордкович. Задачник 9 класс]

Найдите b ₁ и q для геометрической прогрессии ( b _n ), заданной следующими условиями:

Знаменатель геометрической прогрессии

Формула 2-го члена геометрической прогрессии:

Формула 5-го члена геометрической прогрессии:

Получаем систему уравнений

;

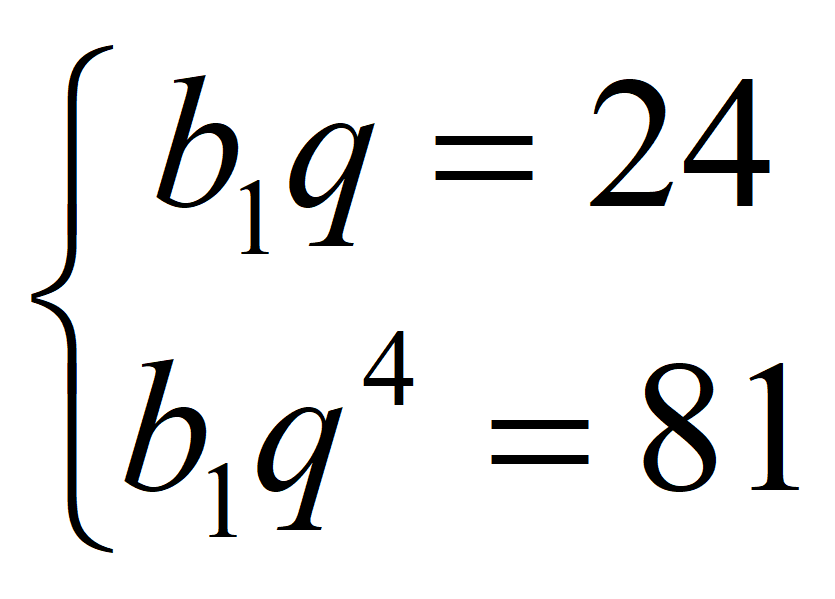
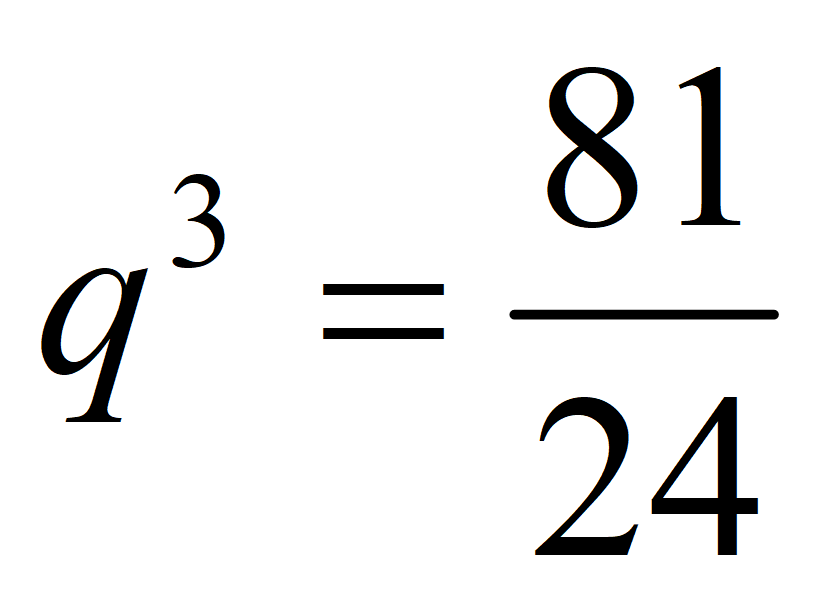
10 класс

Признак делимости на 11

Признак делимости на 7 или 13

Натуральное число делится на 7 или 13, если алгебраическая сумма чисел

Простые и составные числа

Составным называется число, имеющее больше двух делителей.

Число 1 не является ни простым, ни составным, так как делится лишь на 1.

Произвольное натуральное число, большее 1 имеет как минимум один простой делитель.

Множество простых чисел бесконечно [10].

Расстояние между двумя соседними простыми числами может быть больше любого наперед заданного натурального числа [10].

Обратные тригонометрические функции

Тригонометрические формулы

Сложение и вычитание аргументов

Формулы двойного угла

sin 2 α = 2 sinαcosα

Формулы понижения степени

Сложение и вычитание функций

Преобразование произведения в сумму и разность

Методы решения тригонометрических уравнений

Приравнять к нулю и разбить на множители

Подстановка

Универсальная тригонометрическая подстановка

11 класс

Многочлены от одной переменной

Стандартным видом многочлена p ( x ) является расположение его одночленов по убыванию степеней его одночленов

Два многочлена равны, когда они имеют одинаковые коэффициенты при одинаковых степенях переменной.

Если многочлен p ( x ) делится на многочлен q ( x ), то в результате получается многочлен s ( x ).

Если многочлен p ( x ) не делится на многочлен q ( x ), то в результате получается многочлен s ( x ) плюс остаток r ( x ), степень которого меньше степени многочлена q ( x ).

Вы можете поддержать развитие сайта с помощью платежной формы ниже.

Также Вы можете оплатить консультационные и прочие услуги Ольшевского Андрея Георгиевича

Источник