что нужно знать чтобы декодировать закодированное сообщение
Что нужно знать чтобы декодировать закодированное сообщение
В процессах восприятия, передачи и хранения информации живыми организмами, человеком и техническими устройствами происходит кодирование информации. В этом случае информация, представленная в одной знаковой системе, преобразуется в другую. Каждый символ исходного алфавита представляется конечной последовательностью символов кодового алфавита. Эта результирующая последовательность называется информационным кодом (кодовым словом, или просто кодом).
Примерами кодов являются последовательность букв в тексте, цифр в числе, двоичный компьютерный код и др.
Код состоит из определенного количества знаков (имеет определенную длину), которое называется длиной кода. Например, текстовое сообщение состоит из определенного количества букв, число — из определенного количества цифр.
Преобразование знаков или групп знаков одной знаковой системы в знаки или группы знаков другой знаковой системы называется перекодированием.
При кодировании один символ исходного сообщения может заменяться одним или несколькими символами нового кода, и наоборот — несколько символов исходного сообщения могут быть заменены одним символом в новом коде. Примером такой замены служат китайские иероглифы, которые обозначают целые слова и понятия.
Кодирование может быть равномерным и неравномерным. При равномерном кодировании все символы заменяются кодами равной длины; при неравномерном кодировании разные символы могут кодироваться кодами разной длины (это затрудняет декодирование). Неравномерный код называют еще кодом переменной длины.
Примером неравномерного кодирования является код азбуки Морзе. Длительное время он использовался для передачи сообщений по телеграфу. Кодовый алфавит включал точку, тире и паузу. При передаче по телеграфу точка означала кратковременный сигнал, тире — сигнал в 3 раза длиннее. Между сигналами букв одного слова делалась пауза длительностью одной точки, между словами — длительностью трех точек, между предложениями — длительностью семи точек.
Вначале код Морзе был создан для букв английского алфавита, цифр и знаков препинания. Принцип этого кода заключался в том, что часто встречающиеся буквы кодировались более простыми сочетаниями точек и тире. Это делало код компактным. Позже код был разработан и для символов других алфавитов, включая русский.
Коды Морзе для некоторых букв.
Чтобы избежать неоднозначности, код Морзе включает также паузы между кодами разных символов.
Декодирование информации
В зависимости от системы кодирования информационный код может или не может быть декодирован однозначно. Равномерные коды всегда могут быть декодированы однозначно.
Для однозначного декодирования неравномерного кода важно, имеются ли в нем кодовые слова, которые являются одновременно началом других, более длинных кодовых слов.
Закодированное сообщение можно однозначно декодировать с начала, если выполняется условие Фано: никакое кодовое слово не является началом другого кодового слова.
Закодированное сообщение можно однозначно декодировать с конца, если выполняется обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова.
Неравномерные коды, для которых выполняется условие Фано, называются префиксными. Префиксный код — такой неравномерный код, в котором ни одно кодовое слово не является началом другого, более длинного слова. В таком случае кодовые слова можно записывать друг за другом без разделительного символа между ними.
Например, код Морзе не является префиксным — для него не выполняется условие Фано. Поэтому в кодовый алфавит Морзе, кроме точки и тире, входит также символ–разделитель — пауза длиной в тире. Без разделителя однозначно декодировать код Морзе в общем случае нельзя.
Конспект урока по информатике «Кодирование и декодирование информации».
Что нужно знать чтобы декодировать закодированное сообщение
Тема: Кодирование и декодирование информации.
· кодирование – это перевод информации с одного языка на другой (запись в другой системе символов, в другом алфавите)
· обычно кодированием называют перевод информации с «человеческого» языка на формальный, например, в двоичный код, а декодированием – обратный переход
· один символ исходного сообщения может заменяться одним символом нового кода или несколькими символами, а может быть и наоборот – несколько символов исходного сообщения заменяются одним символом в новом коде (китайские иероглифы обозначают целые слова и понятия)
· кодирование может быть равномерное и неравномерное;
при равномерном кодировании все символы кодируются кодами равной длины;
при неравномерном кодировании разные символы могут кодироваться кодами разной длины, это затрудняет декодирование
· закодированное сообщение можно однозначно декодировать с начала, если выполняется условие Фано: никакое кодовое слово не является началом другого кодового слова;
· закодированное сообщение можно однозначно декодировать с конца, если выполняется обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова;
· условие Фано – это достаточное, но не необходимое условие однозначного декодирования.
Пример задания:
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А–00, Б–010, В–011, Г–101, Д–111. Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно? Коды остальных букв меняться не должны. Выберите правильный вариант ответа.
1) для буквы Б – 01 2) это невозможно
3) для буквы В – 01 4) для буквы Г – 01
Решение (1 способ, проверка условий Фано):
1) для однозначного декодирования достаточно, чтобы выполнялось условие Фано или обратное условие Фано;
2) проверяем последовательно варианты 1, 3 и 4; если ни один из них не подойдет, придется выбрать вариант 2 («это невозможно»);
«прямое» условие Фано не выполняется (код буквы Б совпадает с началом кода буквы В);
«обратное» условие Фано не выполняется (код буквы Б совпадает с окончанием кода буквы Г); поэтому этот вариант не подходит ;
«прямое» условие Фано не выполняется (код буквы В совпадает с началом кода буквы Б);
«обратное» условие Фано не выполняется (код буквы В совпадает с окончанием кода буквы Г); поэтому этот вариант не подходит ;
«прямое» условие Фано не выполняется (код буквы Г совпадает с началом кодов букв Б и В); но «обратное» условие Фано выполняется (код буквы Г не совпадает с окончанием кодов остальных буквы); поэтому этот вариант подходит ;
Решение (2 способ, дерево):
1) построим двоичное дерево, в котором от каждого узла отходит две ветки, соответствующие выбору следующей цифры кода – 0 или 1; разместим на этом дереве буквы А, Б, В, Г и Д так, чтобы их код получался как последовательность чисел на рёбрах, составляющих путь от корня до данной буквы (красным цветом выделен код буквы В – 011):
2) здесь однозначность декодирования получается за счёт того, что при движении от корня к любой букве в середине пути не встречается других букв (выполняется условие Фано);
3) теперь проверим варианты ответа: предлагается перенести одну из букв, Б, В или Г, в узел с кодом 01, выделенный синим цветом
4) видим, что при переносе любой из этих букв нарушится условие Фано; например, при переносе буквы Б в синий узел она оказывается на пути от корня до В, и т.д.; это значит, что предлагаемые варианты не позволяют выполнить прямое условие Фано
5) хочется уже выбрать вариант 2 («это невозможно»), но у нас есть еще обратное условие Фано, для которого тоже можно построить аналогичное дерево, в котором движение от корня к букве дает её код с конца (красным цветом выделен код буквы В – 011, записанный с конца):
видно, что обратное условие Фано также выполняется, потому что на пути от корня к любой букве нет других букв
6) в заданных вариантах ответа предлагается переместить букву Б, В или Г в синий узел; понятно, что Б или В туда перемещать нельзя – перемещённая буква отказывается на пути от корня к букве Г; а вот букву Г переместить можно, при этом обратное условие Фано сохранится
Ещё пример задания:
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приёмной стороне канала связи. Использовали код:
А–1, Б–000, В–001, Г–011. Укажите, каким кодовым словом должна быть закодирована буква Д. Длина этого кодового слова должна быть наименьшей из всех возможных. Код должен удовлетворять свойству однозначного декодирования.
1) 00 2) 01 3)11 4) 010
8) заметим, что для известной части кода выполняется условие Фано – никакое кодовое слово не является началом другого кодового слова
9) если Д = 00, такая кодовая цепочка совпадает с началом Б = 000 и В = 001, невозможно однозначно раскодировать цепочку 000000: это может быть ДДД или ББ; поэтому первый вариант не подходит
10) если Д = 01, такая кодовая цепочка совпадает с началом Г = 011, невозможно однозначно раскодировать цепочку 011: это может быть ДА или Г; поэтому второй вариант тоже не подходит
11) если Д = 11, условие Фано тоже нарушено: кодовое слово А = 1 совпадает с началом кода буквы Д, невозможно однозначно раскодировать цепочку 111: это может быть ДА или ААА; третий вариант не подходит
12) для четвертого варианта, Д = 010, условие Фано не нарушено;
· условие Фано – это достаточное, но не необходимое условие однозначного декодирования, поэтому для уверенности полезно найти для всех «неправильных» вариантов контрпримеры: цепочки, для которых однозначное декодирование невозможно
Еще пример задания:
Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11, соответственно). Если таким способом закодировать последовательность символов БАВГ и записать результат шестнадцатеричным кодом, то получится
14) из условия коды букв такие: A – 00, Б –01, В – 10 и Г – 11, код равномерный
15) последовательность БАВГ кодируется так: 01 00 10 11 = 1001011
16) разобьем такую запись на тетрады справа налево и каждую тетраду переведем в шестнадцатеричную систему (то есть, сначала в десятичную, а потом заменим все числа от 10 до 15 на буквы A, B, C, D, E, F); получаем
1001011 = 0100 10112 = 4B 16
17) правильный ответ – 1.
· расчет на то, что при переводе тетрад в шестнадцатеричную систему можно забыть заменить большие числа (10–15) на буквы (10112 = 11, получаем неверный ответ 41116)
· может быть дан неверный ответ, в котором нужные цифры поменяли местами (расчет на невнимательность), например, B 416
· в ответах дана последовательность, напоминающая исходную (неверный ответ BACD 16), чтобы сбить случайное угадывание
Еще пример задания:
Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв – из двух бит, для некоторых – из трех). Эти коды представлены в таблице:
Кодирование и декодирование информации
Вы будете перенаправлены на Автор24
Кодирование информации
Для осуществления полноценного процесса передачи информации, при котором сам процесс должен успешно завершиться, а сообщение дойти от отправителя до получателя в полном объеме, который, в свою очередь, его правильно трактует, информацию необходимо закодировать.
Кодирование — это преобразование информации из одной ее формы представления в другую, наиболее удобную для её хранения, передачи или обработки.
Способы кодирования информации бывают различные и зависят они, в первую очередь, от целей кодирования.
Наиболее распространенными из которых являются:
Чаще всего кодированию подвергаются тексты на естественных языках (русском, английском и пр.).
Цели кодирования заключаются в доведении идеи отправителя до получателя, обеспечении такой интерпретации полученной информации получателем, которая соответствует замыслу отправителя. Для этого используются специальные системы кодов, состоящие из символов и знаков. Код представляет собой систему условных знаков (символов), предназначенных для представления информации по определенным правилам. В настоящее время понятие «код» трактуется по-разному.
Некоторые авторы (Р. Бландел, А. Б. Зверинцев, В. Г. Корольке и др.) понимают коды как любую форму представления информации или же как набор однозначных правил, используя которые сообщение можно представить в той или иной форме. Согласно этому определению человеческая речь может выступать в качестве одного из кодов. Это может означать, что в результате кодирования сообщение преобразуется в последовательность, состоящую из произносимых слов.
Готовые работы на аналогичную тему
Другим вариантом трактовки термина «код», сформированного в технической среде под влиянием «математической теории связи (коммуникации)» и использования технических средств коммуникации, является условное преобразование, как правило, взаимно однозначное и обратимое, используя которое сообщения преобразовываются из одной системы знаков в другую. К примерам такого преобразования относят азбуку Морзе, семафорный код и жесты глухонемых. Для данного определения характерно четкое различие языка, который развивался вместе с человеком на протяжении всего этапа эволюции, и кодов, разработанных людьми для определенных целей и подчиняющихся четко сформулированным правилам.
В теории коммуникации кодирование представляют как соответствующую переработку исходной идеи сообщения с целью ее доведения до адресата. При этом в разных конкретных случаях формы передачи информации могут быть различными, например: брошюры, листовки, рекламные ролики па заданную тему и т.д.
Декодирование информации
Декодирование — процесс восстановления изначальной формы представления информации, т. е. обратный процесс кодирования, при котором закодированное сообщение переводится на язык, понятный получателю. В более широком плане это:
а) процесс придания определенного смысла полученным сигналам;
б) процесс выявления первоначального замысла, исходной идеи отправителя, понимания смысла его сообщения.
Если получатель правильно воспримет смысл сообщения, то его реакция будет именно такой, какую и ожидал от него отправитель сообщения. То, каким образом получатель будет расшифровывать сообщение, зависит, как правило, от его индивидуальных особенностей восприятия информации. Так как каждый человек в той или иной степени предвзято и субъективно оценивает события, то, соответственно разные люди воспринимают и понимают одни и те же события по-разному. И это непременно необходимо учитывать при трансляции информации и при коммуникации между людьми.
Модель кодирования/декодирования С. Холла
Особенности системы кодирования-декодирования, которая включает в себя обработку информационного сообщения с целью его передачи и осмысления потребителем, лучше всего рассмотреть на примере коммуникационной модели С. Холла. В основу его теории положены базовые принципы семиотики структурализма, которые предполагают, что любое смысловое сообщение можно сконструировать из знаков, имеющих как явные, так и подразумеваемые смыслы в зависимости от выбора, осуществляемого кодировщиком, т.е. коммуникатором. Согласно основному положению семиотики многообразие смыслов зависит от природы языка, являющегося инструментарием информационной системы, и от смысловых значений, которые заключены в комбинациях знаков и символов в рамках определенной социальной культуры, к которой принадлежат отправитель (кодировщик) и получатель (декодировщик).
Семиотика подчеркивает семантическую силу закодированного текста, рассматривает смысл информационного сообщения прочно внедренного в текст. С. Холл принимал базовые положения этого подхода, но, в свою очередь, внес в него ряд дополнений.
Согласно Холлу коммуникаторы часто кодируют сообщения, придерживаясь идеологических и пропагандистских целей, а для этого манипулируют языком и медиасредствами (сообщения приобретают «предпочтительный» смысл).
Получатели согласно Холлу не всегда обязаны принимать и декодировать сообщения в том виде, в котором они отправлены. Получатели оказывать сопротивление идеологическому влиянию, применяя при этом альтернативные оценки в соответствии со своим мировоззрением, опытом и взглядами на окружающую систему бытия.
Свою теорию С. Холл сформулировал, используя в качестве примера работу телевидения, но ее можно применить к любым видам средств массовой информации. Суть теории заключается в том, что медиасообщение, проходя на своем пути от источника до получателя, претерпевает ряд преобразований. В результате средства медиакоммуникации передают сообщения, конформные или оппозиционные по отношению к правящим властям, различным общественным, политическим и экономическим социальным институтам. Эти сообщения кодируются зачастую в форме устоявшихся содержательных жанров (к ним можно отнести новости политического, спортивного, экономического содержания; музыкальные передачи, сериалы и пр., в общем все то, что смотрят обыватели), имеющих очевидный содержательный смысл, актуализированную направленность и встроенные руководства для их интерпретации заинтересованной целевой аудиторией. Зрители же, в свою очередь, подходят к содержанию, предлагаемому СМИ, с другими «смысловыми структурами», которые строятся на их собственном здравом смысле, идеях и опыте.
Различные группы людей (или так называемые субкультуры) занимают разные социальные и культурные ниши этнопространства и по-разному воспринимают сообщения СМИ. В результате своих исследований С. Холл пришел к выводу, что декодированный смысл сообщения не обязательно должен совпадать с первоначальным смыслом, который был закодирован, хотя он и был опосредован уже сложившимися медиажанрами и общей языковой системой. Важным является и то, что декодирование может принимать направления, отличные от предполагаемого, т.е. получатели, образно говоря, могут читать между строк и даже сознательно искажать изначально заложенный смысл сообщения.
Теория Холла содержит ряд принципиальных положений, это:
Таким образом, мы пришли к определению того, кто такой получатель.
Получатель — это лицо, для которого предназначена передаваемая информация, и которое может интерпретировать ее. Получателю, чтобы понять смысл передаваемого сообщения, нужно его раскодировать (декодировать). В качестве получателя могут выступать как один человек, так и группа лиц, общество в целом или любая его часть. Когда в качестве получателя выступает более одного человека, то это называют аудиторией коммуникации.
Получатель информационного сообщения должен обладать определенными характеристиками, которые представляю собой важные факторы, влияющие на эффективность коммуникации. Главным условием при этом становится способность получателя воспринимать и декодировать отправленное ему сообщение. Эта способность зависит от профессиональной компетентности получателя, его жизненного опыта, принадлежности к той или иной группе, ценностных ориентаций, общей культуры, образовательного и интеллектуального уровня, а также обусловлена социокультурными рамками коммуникативного процесса. Реакция получателя представляет собой основной индикатор эффективности коммуникации.
Мы подробно с вами разобрали непосредственно саму теорию кодирования и декодирования информационных сообщений, в частности модель Холла, которая в большей степени ориентируется на социум.
Однако эти два процесса широко используются во всех сферах жизнедеятельности человека: медицине, технике, образовании и т.д. И каждый из нас ежедневно с ними сталкивается независимо от того, что происходит в окружающей нас жизни.
Кодирование и декодирование информации – история развития, для чего нужно и где используется
Рассмотрим детальнее, что такое кодирование сообщений, а также декодирование информации.
Для передачи информации люди используют естественные языки.
В повседневной жизни мы общаемся с помощью неформальной речи, а в деловой сфере используем формальный язык.
Сегодня для передачи и отображения информации мы используем вычислительную технику, которая «не понимает» наш язык без специальных операций – кодирования и декодирования.
Рассмотрим эти понятия детальнее, а также все виды и наглядные примеры кодирования/декодирования.
Базовые понятия
Прежде чем разобраться с основами процедуры кодирования, следует ознакомиться с несколькими простейшими понятиями.
К примеру, компьютер, смартфон, ноутбук и любые другие компьютерные устройства работают с двоичным кодом.
В компьютерной технике кодирование происходит, когда пользователь вводит любую информацию в систему – создает файлы, печатает текст и так далее.
Для понимания обычных букв кириллицы или латиницы они превращаются в набор нолей и единиц.
Чтобы отобразиться на экране компьютера, система проводит декодирование числовой последовательности и выводит результат на экран.
Все эти действия выполняются за тысячные доли секунды.
История развития кодирования
Телеграф Шаппа
Первым техническим средством кодирования данных был созданный в 1792 году телеграф Шаппа.
Устройство передавало оптическую информацию в простейшем виде с помощью специальной таблицы кодов, в которой каждой букве латинского алфавита соответствовала одна фигура.
В результате, телеграф мог отобразить и передать набор фигур.
Скорость передачи таких сообщений составляла всего два слова в минуту.
Телеграф Морзе
Созданный в 1837 году телеграф Морзе стал революционном устройством кодирования/декодирования информации.
Принцип кодирования заключался в преобразовании любого сообщения в три символа алфавита:
Подобная связь используется по сей день в мореходной сфере для мгновенной передачи сообщений между суднами.
Радиоприёмник
В 1899 году А. Попов создал первый в мире беспроводной телеграф или радиоприемник.
Принцип его работы заключался в кодировании электрических сигналов азбукой Морзе и её дальнейшей передаче на длительные расстояния.
Позже был изобретен телеграф Бодо, который решал проблему неравномерности кода и сложность декодирования.
Читайте также:
Современные способы кодирования данных
Для перевода информации в код могут быть использованы разные способы и алгоритмы кодирования.
Использование каждого из методов зависит от среды, цели и условий создания кода.
С разными алгоритмами кодирования мы сталкиваемся в повседневной жизни:
Полезная информация:
Обратите внимание на программу Hex Editor. Это утилита, выступающая в качестве шестнадцатеричного редактора. Осуществляет поддержку работы с файлами, которые хранятся на жестком диске и оперативной памяти.
Двоичное кодирование и другие числовые системы
Самый простой и распространенный способ кодирования – это представление информации в двоичном (бинарном) коде.
С его помощью работают все компьютеры и вычислительные системы.
Компьютер может выполнять сверхбыстрые вычисления с помощью только двух условий – наличия тока и его напряжение.
С помощью единиц передается высокое напряжение, а с помощью нолей – низкое.
Для перевода привычных нам слов, цифр и символов в десятичное представление следует использовать специальные таблицы конверсии.
На рисунке ниже изображена таблица для цифровой и символьной раскладки, а также для букв латиницы.
К примеру, в результате перевода фразы «Hello, how are you?» получим последовательность «10010001000101100110010011001001111010110001000001001000100111110101110100001000001101001010001010100000101100110011111010101».
Чтобы выполнить декодирование информации, необходимо разделить бинарный код на части, каждая из которых равна семи ячейкам:
Также, в теории кодирования можно встретить не только двоичную систему, но и троичную, четвертую, пятую, шестую…шестнадцатеричную и другие системы.
Шестнадцатеричная система исчисления используется в языках программирования низкого уровня.
Таким образом, удаётся добиться более быстрого выполнения кода центральным процессором. Примером такого языка является машинный код ассемблер.
Так шестнадцатеричная система декодируется в двоичную.
Рис.3 – пример декодирования зыков программирования разных уровней
Также, шестнадцатеричная система используется в создании программной документации, так намного проще записывать байты.
Для обозначения одного байта требуется только две шестнадцатеричные цифры, а не восемь, как в двоичной системе.
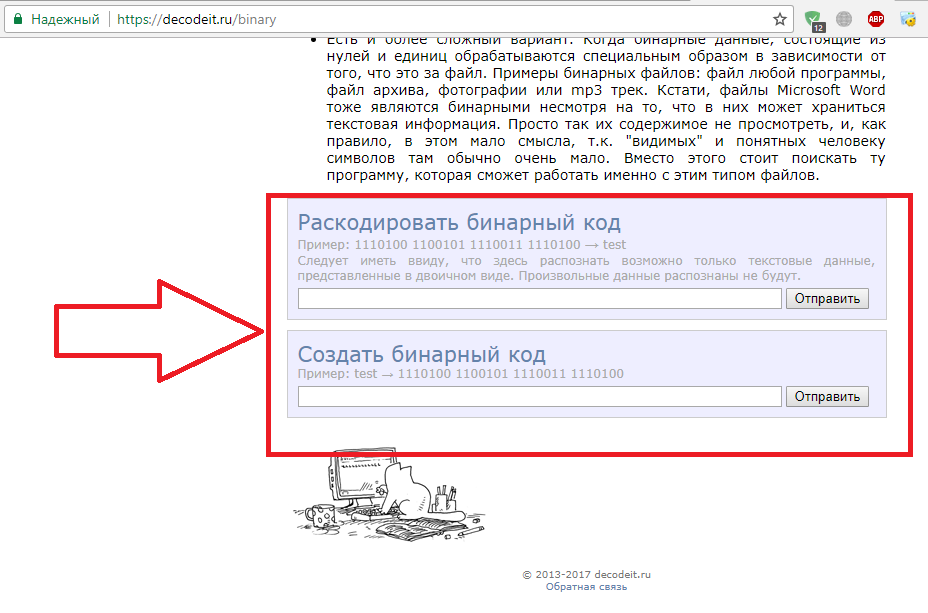
Онлайн-кодировщики
Для быстрого преобразования любого текста в набор символов бинарной или других систем исчисления удобнее использовать автоматические кодировщики.
Также, они могут декодировать текст, самостоятельно определяя, какую систему использовал пользователь для кодировки.
Рис.4 — Сервис DecodeIT
Кодирование символов
Для кодирования символов используются различные стандарты, среди которых Юникод, ASCII, UTF-8 и другие.
Зачем нужна кодировка символов?
Любые символы на экране компьютера или смартфона отображаются за счет двух вещей:
Знаки – это шрифты, которые поддерживаются устройством. В ОС Windows они находятся в окне Панель управления (директория «Шрифты»).
С помощью этой папки вы можете добавлять или удалять существующие представления символов.
Таким образом, на экране появляется буква и текст.
За установку шрифтов отвечает операционная система вашего компьютера, а за кодировку текста – программы, в которых вы набираете или просматриваете текстовые данные.
Разбирая код, приложение обрабатывает кодировку знака и ищет его соответствие в поддерживаемом для этого же документа шрифте.
Если соответствие не найдено, вместо текста вы увидите набор непонятных символов.
Рис.5 – пример ошибки кодирования символов в Блокноте Windows
Чтобы символы кириллицы и латиницы открывались без проблем в большинстве программ, было предложено ввести стандарты кодирования.
Один из наиболее популярных – это Юникод (или Unicode).
Он поддерживается практически всеми существующими шрифтами и программным обеспечением.
Также, широко используются технологии UTF-8, ASCII.
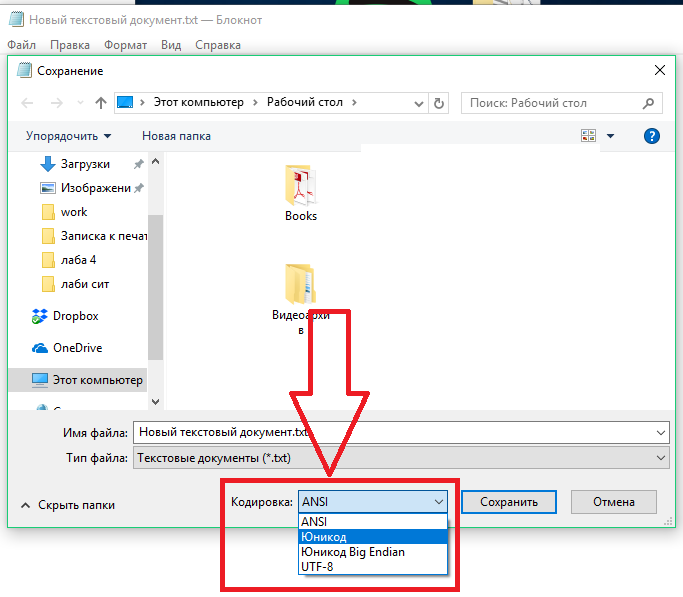
Для этого достаточно зайти в настройки текстового редактора и сохранить файл с кодировкой Юникод или другими популярными форматами кодирования.
Затем откройте файл заново, текст должен отображаться в нормальном режиме.
Рис.6 – декодирование текста в редакторе
Читайте также:
Шифрование
Часто возникает необходимость не только закодировать информацию, но и скрыть её содержимое от посторонних.
Для таких целей используется шифрование.
Простыми словами, шифрование – это кодирование информации, но не с целью её корректного представления на экране компьютера, а с целью сокрытия данных от тех, кому не положено получать доступ к шифрованной информации.
Алфавит шифрования состоит из двух элементов:
Дешифрование – это обратный процесс к защитному кодированию, который подразумевает превращение данных в первоначальный вид с помощью известного ключа.
Криптография – это наука о шифровании данных. Всего различают два раздела криптографии:
Где используется криптография?
Кодирование информации с целью шифрования используется уже более трех тысяч лет.
Истории известны первые попытки шифрованной передачи сообщений между известными полководцами царями и просто высокопоставленными людьми.
Также, шифрованное кодирование используется в обычных социальных сетях, мессенджерах.
К примеру, Telegram – мессенджер, главной особенностью которого является кодирование сообщений пользователей таким образом, чтобы никто посторонний не смог взломать переписку.
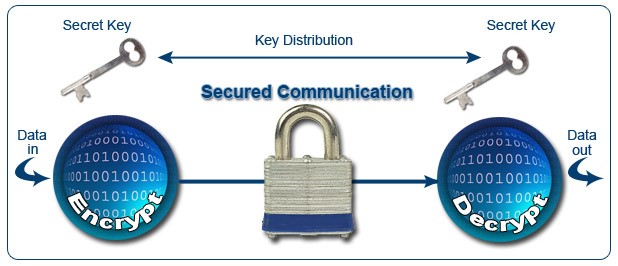
Также, алгоритмы шифрования встроены во все операционные системы, облачные хранилища.
Они нужны для защиты ваших личных данных.
Рис.7 – принцип работы защищенного соединения
Стеганография
Он схож с упомянутой выше криптографией, но если основной целью криптографии является защита секретной информации, то стеганография отвечает за сокрытие самого факта о том, что существуют какие-либо защищаемые данные.
Процедура стенографического кодирования подразумевает встраивание сообщения в картинки, музыкальные файлы, видео и так далее.
Каждая буква секретного сообщения кодируется в бинарную форму, затем она заменяет один из пикселей.
Таким образом, можно закодировать даже большие сообщения без какого-либо визуального изменения фотографии, так как на современных гаджетах не видны отдельные пиксели картинки.
Аналогичным образом происходит кодирование звука в музыку, каждой частоте присваивается определенная буква.
Декодировать стенографическую информацию можно только с помощью специальных утилит, которые и зашифровали сообщение или путем взлома.
Достаточно сопоставить картинку до и после встраивания секретного текста, количество пикселей будет отличаться.
Затем используется специальное ПО для перебора и расшифровки каждого пикселя и воссоздания сообщения.
Читайте также:
Кодирование информации используется сотни лет для удобной передачи данных между устройствами.
С развитием технологий и переносом банковской сферы в техническую среду появилась необходимость в использовании алгоритмов кодирования, которые бы шифровали информацию, сохраняя её от несанкционированного доступа.
Сегодня без технологий кодирования данных невозможна работа ни одного компьютера, смартфона, сайта или банковского счета.
Тематические видеоролики:
Богдан Вязовский
«Мы живем в обществе, где технологии являются очень важной частью бизнеса, нашей повседневной жизни. И все технологии начинаются с искр в чьей-то голове. Идея чего-то, чего раньше не существовало, но однажды будет изобретено, может изменить все. И эта деятельность, как правило, не очень хорошо поддерживается»