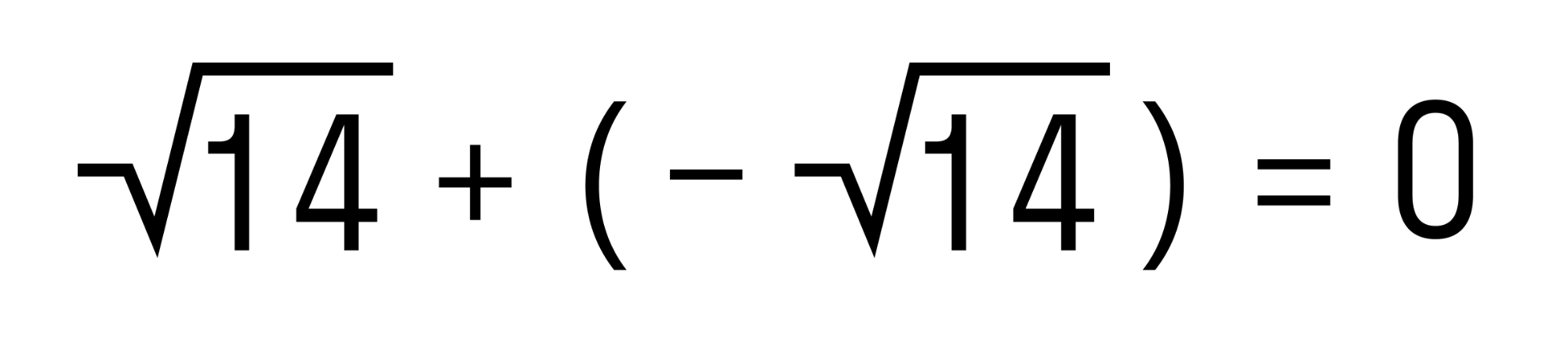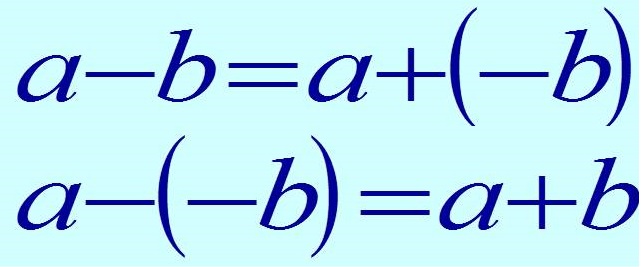что нужно сделать чтобы сложить 2 числа с разными знаками

Сложение чисел с разными знаками

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные определения

Целые числа — это множество чисел, которые состоят из натуральных чисел, целых отрицательных чисел и нуля.

Положительные целые числа — это целые числа со знаком «плюс». Они всегда больше нуля. Примеры положительных целых чисел: 11, 500, 1387.

У каждого положительного числа есть число-близнец, которое отличается только тем, что перед ним стоит знак минус. Такие числа называются противоположными.

Противоположные числа не равны друг другу, но у них есть общее — модуль. Модуль у противоположных чисел одинаковый: у положительного числа он равен самому числу, а у отрицательного — противоположному, то есть положительному. Например:

Действительные числа — это числа, которые могут быть записаны в виде конечной или бесконечной десятичной дроби.

Рациональные числа — это числа, которые можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль.

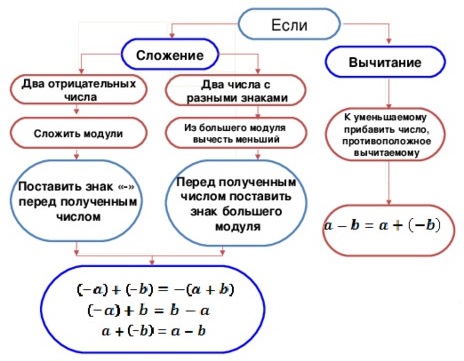
Правило сложения чисел с разными знаками

Положительное число можно рассматривать как доход, а отрицательное — как расходы или долг. Чтобы понять, сколько мы заработали или потратили, нужно смотреть на модули этих чисел.

Например, родители выдали триста рублей на карманные расходы. Если в конце недели у нас осталось немного денег — значит расходов было меньше, чем дохож. А если нам пришлось попросить еще 50 рублей на наклейки — расходы привысили доход. Если же расходы равны доходам, то у нас будет нулевой остаток.

А теперь сформулируем правило сложения чисел с разными знаками.

Чтобы сложить положительное и отрицательное число, нужно:

Это правило сводит сложение чисел с разными знаками к вычитанию из большего положительного числа меньшее число. В результате сложения положительного и отрицательного числа может получиться: положительное число, отрицательное число или нуль.

Повторим еще раз. Чтобы сложить числа с разными знаками:

Алгоритм сложения чисел с разными знаками справедлива для целых чисел, для рациональных чисел и для действительных чисел.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Примеры сложения чисел с разными знаками

Сложение чисел с разными знаками требует внимательности и последовательности. Рассмотрим примеры по правилу выше:

Нам нужно сложить числа с разными знаками. Выполним все шаги по правилу сложения положительного и отрицательного числа.

Чтобы сложить рациональные числа с разными знаками, которые не являются целыми, их следует представить в виде обыкновенных или десятичных дробей.

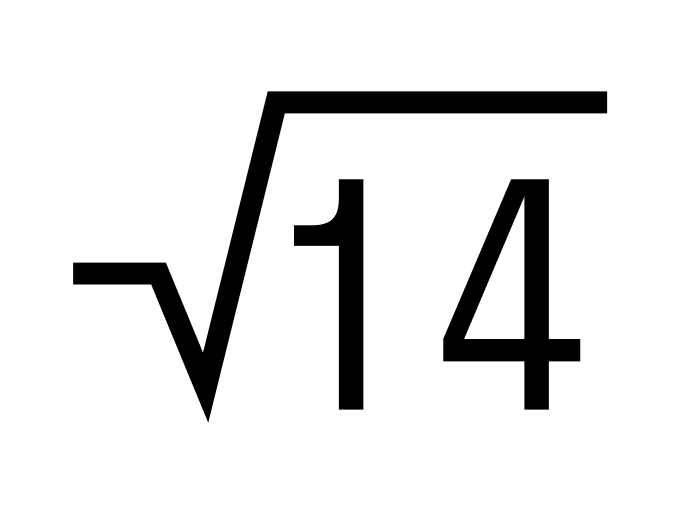
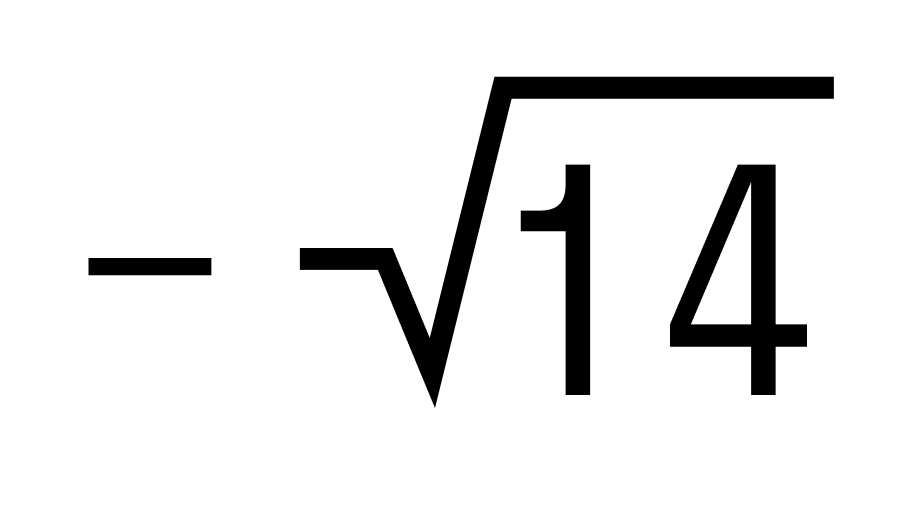
Пример 3. Чему равна сумма чисел и ?

Замечаем, что у складываемых чисел разные знаки, а их модули равны. Значит эти числа являются противоположными, а сумма противоположных чисел равна нулю.

Получается вот так:

Важно помнить, что при сложении действительных чисел с разными знаками результат можно записывать не в виде бесконечной десятичной дроби, а в виде числового выражения, которое содержит корни, степени, логарифмы и прочее.

Источник

Урок 34 Бесплатно Сложение чисел с разными знаками

В одном из прошлых уроков мы научились складывать и вычитать числа с помощью координатной прямой.

Сегодня же мы разберемся как складывать числа с разными знаками, не прибегая к координатной прямой. Также проанализируем, чему может оказаться равна сумма чисел с разными знаками.

Сложение чисел с разными знаками

Допустим, у Василия есть 30 тысяч рублей на счету в банке, но при этом у него есть долг в размере 13 тысяч рублей.

Сложив 30 и -13, мы получим ту сумму, которой Василий может свободно распоряжаться.

Это можно сделать с помощью координатной прямой. Но с большими числами работать по такому алгоритму некомфортно, поэтому есть более простой способ.

Чтобы сложить два числа с разными знаками, необходимо:

1) посчитать их модули

2) из большего модуля вычесть меньший модуль

3) поставить перед полученным числом знак слагаемого с наибольшим модулем

Пример:

1) Модуль 30 равен 30, модуль -13 равен 13

2) \(\mathbf<30>13>\), следовательно вычитаем из 30-ти 13, \(\mathbf<30-13=17>\)

3) Число с наибольшим модулем в данном случае 30, оно положительное, значит, и перед ответом поставим знак «+», но можем просто не ставить ничего.

17 тысячами рублей может распоряжаться Василий.

Также покажем на примере, как может получиться отрицательное число:

Есть другой клиент банка Олег, у него на счету 5500 рублей, а должен он 9300.

Тогда, чтобы понять, сколько у Олега свободных денег, мы должен сложить 5500 и -9300.

2) Вычитаем из наибольшего модуля наименьший:

3) \(\mathbf<9300>5500>\), значит, ответ та кже, как и число -9300, будет числом отрицательным.

Если убрать промежуточные действия, то получится: \(\mathbf<5500+(-9300)=-3800>\)

То, что у Олега получилось отрицательное количество свободных денег показывает, что даже если он отдаст все деньги со счета на погашение долга, он останется должен банку еще 3800 рублей.

Нельзя не упомянуть случай, когда результатом сложения двух чисел с разными знаками является нуль.

Сложим 5 и -5.

1) Точно также считаем модули:

3) У нас получился нуль в прошлом действии, поэтому можно даже не думать о знаке, ибо нуль это и есть нуль.

Тогда получаем: \(\mathbf<5+(-5)=0>\)

Заметим: чтобы получился нуль, у чисел должны быть равные модули. И чтобы это был случай со сложением чисел с разными знаками, одно должно быть отрицательным, а другое положительным.

Тогда получаем, что сумма двух чисел с разными знаками равна нулю тогда и только тогда, когда это противоположные числа.

Пройти тест и получить оценку можно после входа или регистрации

Аналитика суммы двух чисел с разными знаками

Сейчас мы потренируемся отдельно делать некоторые заключения про сумму двух чисел, не считая ее.

Мы уже сказали, что если сумма двух чисел с разными знаками равна нулю, то эти числа являются взаимно обратными.

Это же верно и в обратную сторону. В самом деле, если взять два противоположных числа а и -а, то их модули будут равны а и а соответственно, а значит, их разность будет равна нулю.

Получается, что, если нас просят сложить два числа с разными знаками, мы можем сразу посмотреть, что они противоположны, то есть вдобавок к тому, что у них разные знаки, у них еще и равны модули, и сделать вывод, что их сумма будет равна нулю.

Примеры:

Мы можем использовать это в промежуточных действиях, чтобы не считать сложные части выражения, если они все равно равны нулю:

Да, конечно, посчитать тоже несложно, особенно используя калькулятор, но не считать еще проще и быстрее!

В случаях с числами, которые не являются противоположными, мы, может быть, не сможем так красиво угадать ответ, как это нам только что удавалось выше.

Посмотрев на числа, а если быть точным, только сравнив их модули, можно сказать про знак результата.

В самом деле, в правиле подсчета суммы чисел с разными знаками мы приписываем к разности модулей знак слагаемого с наибольшим модулем.

Значит, если сравним модули чисел, то уже будем знать, какой знак будет у ответа.

Например, какой будет знак у суммы 3-х и \(\mathbf<-68458456>\)-ти?

Очевидно, модуль второго числа будет больше модуля первого числа, потому что у второго числа больше значащих разрядов.

Значит, у результата будет знак второго слагаемого.

Перед ним стоит минус, значит, оно отрицательное, а это значит, что и результат будет числом отрицательным.

Пройти тест и получить оценку можно после входа или регистрации

Решение задач с помощью суммы чисел с разными знаками

Теперь, когда мы знаем, как складывать числа с разными знаками, то можем подумать о том, как применить наши знания для решения задач.

Главным образом, отрицательные числа очень удобны, когда мы говорим о долгах.

Суммируя, сколько в месяц приходит денег (зарплата, деньги за аренду квартиры, доход по процентам с денег, лежащих в банке), а также, сколько мы должны заплатить кому-либо (налоги, коммунальные услуги, подписки на интернет-сервисы), мы можем посчитать, сколько свободных денег у нас останется на прочие нужды.

Для этого мы должны считать любой наш доход со знаком «плюс», а любой расход или долг со знаком «минус».

Пример:

Александр работает на заводе и получает 40 тысяч рублей в месяц зарплатой, также он сдает одну из своих квартир за 20 тысяч рублей, при этом он должен платить 5 тысяч рублей за коммунальные услуги в своей квартире и 169 рублей за подписку на музыкальный сервис.

Сколько денег у Александра остается после уплаты обязательных платежей?

Решение:

Для начала нам нужно понять, с каким знаком суммировать те или иные пункты.

Зарплата и доход от сдачи квартиры являются статьями дохода. Они увеличивают количество денег у Александра, следовательно, должны считаться со знаком «+».

При записи мы не будем писать излишний знак «+», так как он и так подразумевается, если другого знака не стоит.

Коммунальные услуги и оплата за интернет-подписку являются статьями расхода и должны считаться со знаком «-».

Также необходимо привести все единицы измерения к одному виду.

Значит, мы должны либо домножить зарплату, аренду и коммунальные платежи на тысячу, либо же на тысячу разделить плату за интернет-подписку.

Для примера выберем первый путь и приводим к одним единицам величины:

\(\mathbf<40\cdot1000=40000>\) (рублей)- зарплата Александра

\(\mathbf<20\cdot1000=20000>\) (рублей)- Александр получает от сдачи квартиры в аренду

\(\mathbf<5\cdot1000=5000>\) (рублей)- плата за коммунальные услуги

Тогда у нас получается такое выражение для количества оставшихся денег:

\(\mathbf<40000+20000-5000-169=54831>\) (рубль) у Александра остается на прочие расходы.

Ответ: 54831 рубль

Пройти тест и получить оценку можно после входа или регистрации

Дополнительная информация

В этом уроке мы затронули тему долгов и кредитов. Давайте узнаем историю этого явления в мире.

Свое начало кредитование берет еще в Древнем Египте, Вавилоне, Ассирии.

Тогда все было довольно строго, и, если человек не мог вернуть долг, он становился рабом кредитора.

В то время одалживать могли даже не деньги, а, например, зерно, чтобы вырастить больше урожая.

В Древней Греции кредиторами являлись в основном храмы, так как они накапливали в себе богатства и могли помогать в случае неурожая.

Тогда появилось понятие долговая яма: должник помещался в яму до оплаты кредита или, опять же, до перехода в рабство.

В Средние века кредитной системе было несколько сложно, так как церковь, имевшая тогда значительную власть, запретила зарабатывать на процентах, что лишило дохода ростовщиков и банкиров того времени.

Затем в XVI веке запрет на заработок от процентов отменяется и появляются профессиональные банки. Однако власть продолжала их регулировать, не давая сделать процент по кредиту слишком высоким.

Современный вид кредиты начали принимать во время промышленной революции. У банков начала появляться широкая сеть отделений, и кредиты стали доступны обычным людям, а не только высшим слоям общества, как это могло быть раньше.

Несмотря на доступность кредитов в современном мире, нужно всегда просчитывать экономические решения, а в этом деле как раз помогает математика.

Заключительный тест

Пройти тест и получить оценку можно после входа или регистрации

Источник

Сложение чисел с разными знаками: правило, примеры

В этом материале мы расскажем, как правильно выполнять сложение отрицательного и положительного числа. Сначала мы приведем основное правило такого сложения, а потом покажем, как оно применяется при решении задач.

Основное правило сложения положительных и отрицательных чисел

Мы уже говорили ранее, что положительное число можно рассматривать как доход, а отрицательное – как убыток. Чтобы узнать величину дохода и расхода, надо смотреть на модули этих чисел. Если в итоге окажется, что наши расходы превышают доходы, то после их взаимного учета мы останемся должны, а если наоборот, то мы останемся в плюсе. Если же расходы равны доходам, то у нас будет нулевой остаток.

Используя приведенные выше рассуждения, можно вывести основное правило сложения чисел с разными знаками.

Для сложения положительного числа с отрицательным необходимо найти их модули и выполнить сравнение. Если значения окажутся равны, то мы имеем два слагаемых, которые являются противоположными числами, и их сумма будет нулевой. Если же они не равны, то нам надо учесть, что результат будет иметь тот же знак, что и большее число.

Таким образом, сложение в данном случае сводится к вычитанию из большего числа меньшего. Итог этого действия может быть разным: мы можем получить как положительное, так и отрицательное число. Нулевой результат тоже возможен.

Это правило распространяется на целые, рациональные и действительные числа.

Задачи на сложение положительного числа с отрицательным

Разберем, как применять на практике правило, озвученное выше. Возьмем для начала простой пример.

Решение

Если в условиях задачи стоят рациональные числа с разными знаками, не являющиеся при этом целыми, то для удобства расчетов нужно представить их в виде десятичных или обыкновенных дробей. Возьмем такую задачу и решим ее.

Решение

Первым делом переведем смешанное число в обыкновенную дробь. Если вы не помните, как это делается, перечитайте соответствующую статью.

Далее вычтем из большего модуля меньший (см. материал о том, как найти разность дробей с одинаковыми знаменателями):

Запишем весь ход решения:

Решение

Источник

Правило сложения отрицательных чисел и чисел с разными знаками

Для суммирования двух отрицательных чисел, необходимо:

суммировать их модули;

перед полученной суммой поставить знак «минус».

В данном случае, складываем модули 9 и 6, и перед получившимся натуральным числом 15 ставим знак «-«.

Сложение рациональных или дробных чисел выполняется аналогичным способом:

К 26,35 прибавляем 25,35 (т. е. мы складываем модули), в итоге получаем 51,75 с отрицательным значением. Перед ним ставим знак «минус».

Для суммирования натуральных чисел со знаками «+» и «-», надо:

из слагаемого с большим значением модуля вычесть слагаемое с меньшим значением;

перед полученным результатом поставить знак того слагаемого, которое имело большее значение.

61,2 + (-31,5) = + (61,2 — 31,5) = 30,5

Модуль большего числа со знаком «+», соответственно, сумма получилась положительная:

Большее число со знаком «-», поэтому заменяем плюс на минус и получаем отрицательный ответ.

Как вычитать отрицательные и положительные числа

Для нахождения разности противоположных чисел, надо к уменьшаемому прибавить вычитаемое с противоположным знаком, то есть заменить разность суммой.

Наглядно данное действие лучше представить в виде формулы:

То есть любое выражение, содержащее знаки сложения и вычитания, следует решать как сумму чисел.

-6,1 + 5,6 = 5,6 + (-6,3) = 0,5.

Разность выражения будет положительной, если уменьшаемое больше вычитаемого, и отрицательной, если значение модуля уменьшаемого меньше вычитаемого. В случае, когда уменьшаемое и вычитаемое одинаковые, их разность будет равна нулю.

Если нужно отнять отрицательное число, то два знака «минус» подряд дают знак «плюс».

Все вышеперечисленные действия возможно выполнить на калькуляторе. Для этого достаточно ввести сначала модуль числа, потом нажать кнопку изменения знака «+/-».

Заключение

Для закрепления изученных правил можно использовать различные методы проверки знаний. На первом этапе лучшим вариантом будет тренажер, с помощью которого решение подобных примеров можно довести до автоматизма.

Так же для закрепления материала подойдет тестирование. Его можно провести в виде самостоятельной работы. В конце изучения всех правил применяется контрольная работа, задания для которой можно подобрать из различных дидактических материалов.

Источник

Вычитание чисел с разными знаками: правила, примеры

Данная статья посвящена числам с разными знаками. Мы будем разбирать материал и пытаться выполнять вычитание между этими числами. В параграфе мы познакомимся с основными понятиями и правилами, которые пригодятся во время решения упражнений и задач. Также в статье представлены подробно разобранные примеры, которые помогут лучше понять материал.

Как правильно выполнять вычитание

Для того, чтобы лучше понять процесс вычитания, следует начать с основных определений.

Данное правило, которое применяется для вычитания чисел с разными знаками, позволяет работать как с положительными, так и с отрицательными числами. Также можно производить процесс вычитания из отрицательного числа из положительного, которое переходит в сложение.

Для того, чтобы закрепить полученную информацию, мы рассмотрим типичные примеры и на практике рассмотрим правило вычитания для чисел с разными знаками.

Примеры упражнений на вычитание

Закрепим материал, рассмотрев типичные примеры.

Для того, чтобы выполнять вычитание дробей, необходимо представлять числа в виде обыкновенных или десятичных дробей. Это зависит от того, с числами какого вида будет удобнее проводить вычисления.

Когда какое-либо число представлено в виде квадратного корня, логарифма, основной и тригонометрических функций, то зачастую результат вычитания может быть записан в виде числового выражения. Чтобы пояснить данное правило, рассмотрим следующий пример.

Значение полученного выражения может быть вычислено максимально точно только в том случае, если это необходимо. Для подробной информации можно изучить другие разделы, связанные с данной темой.

Источник