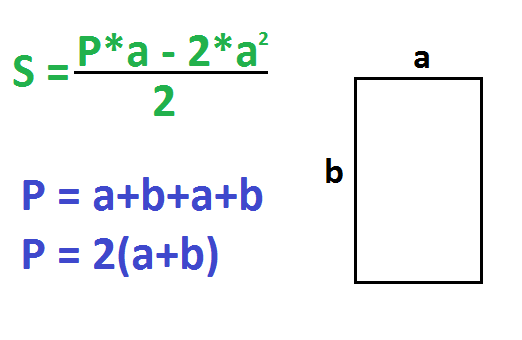что нужно сделать чтобы найти площадь прямоугольника

Как найти площадь прямоугольника – 9 способов с формулами и примерами

Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.

Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.

По диагонали и стороне

Должна быть известна диагональ и любая из сторон. Действия:

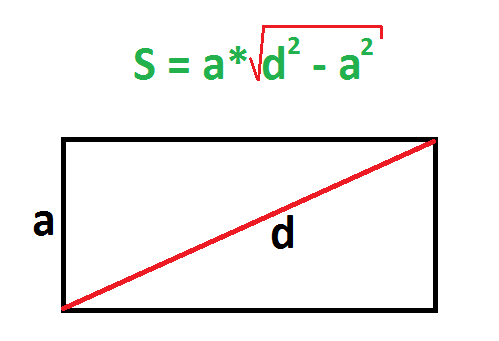
Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.

Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.

По стороне и диаметру описанной окружности

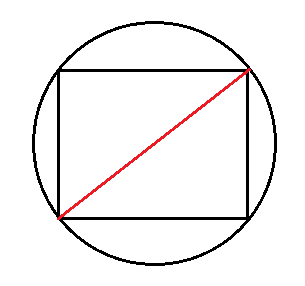
Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.

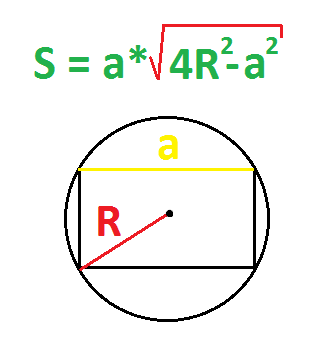
Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.

Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:

А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.

Диаметр равен двум радиусам, потому что радиус – это половина диаметра.

По радиусу описанной окружности и стороне

Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.

Радиус = половине диаметра.

Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.

По стороне и периметру – 1 способ

Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).

Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.

Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.

По стороне и периметру – 2 способ

Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.

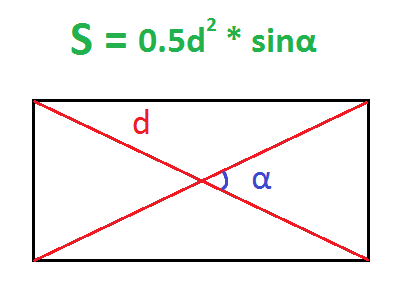
По диагонали и углу между диагоналями

Диагонали прямоугольника всегда равны.

Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.

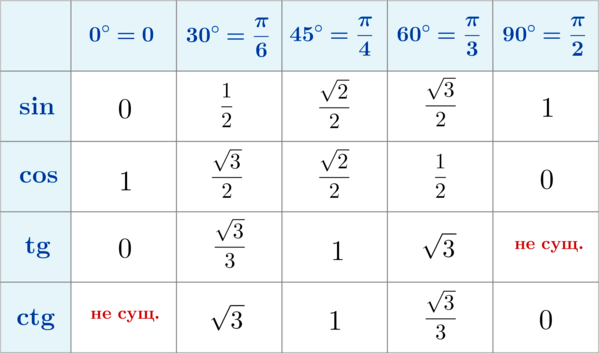
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).

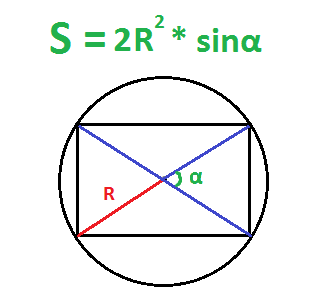
По радиусу описанной окружности и углу между диагоналями – первый способ

Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.

По радиусу описанной окружности и углу между диагоналями – второй способ

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.

Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.

Источник

Площадь прямоугольника

Площадь прямоугольника очень часто требуется найти в задачах по геометрии. И не только — в повседневной жизни очень многие плоскости имеют форму прямоугольника и надо найти площадь прямоугольника. Как это сделать? Давайте рассмотрим все формулы и примеры.

Мы учимся вычислять площадь прямоугольника или площадь прямоугольника в школе. Однако, когда вы станете старше, вполне возможно, что вы не будете помнить, как найти площадь прямоугольника. Для начала давайте вспомним, что такое прямоугольник.

Что такое прямоугольник

Давайте не будем «срезать углы». Чтобы иметь возможность вычислить площадь прямоугольника, естественно, что мы сначала знаем, что это такое. Поэтому для начала необходимо помнить, что прямоугольник является четырехугольником. Другими словами, это геометрическая фигура, которая имеет четыре стороны и четыре прямых угла. Противоположные стороны прямоугольника имеют одинаковую длину. Две самые длинные стороны представляют его длину, а две другие стороны представляют его ширину.

Не все четырехугольники являются прямоугольниками. Действительно, обязательно, чтобы они имели следующие свойства, чтобы мы могли сказать, что это действительно прямоугольник:

Характеристики прямоугольника

Противоположные стороны должны быть параллельны.

Формула площади прямоугольника

Как рассчитать площадь прямоугольника? Обратите внимание, что базовую формулу для вычисления площади (или площади) прямоугольника очень легко запомнить. Вы просто должны умножить его длину на ширину.

Например, площадь прямоугольника длиной 4 сантиметра и шириной 2 сантиметра равна 4 x 2 = 8 см².

Принцип расчета площади прямоугольника

Чтобы вычислить площадь прямоугольника, мы посчитаем количество единиц областей, которые содержит прямоугольник:

В прямоугольнике выше 12 квадратов по 1 см². Его площадь составляет 12 см² (4 х 3).

Примечание. В этом расчете длина L и ширина l прямоугольника должны быть выражены в одной и той же единице длины. Результат будет выражен в той же единице измерения, возведенной в квадрат. Например, если длина прямоугольника выражена в метрах, ширина также должна быть выражена в метрах, а результат формулы для расчета площади прямоугольника даст результат в квадратных метрах (м²).

Пример расчета

Рассмотрим прямоугольник длиной L = 4 см и шириной l = 2 см. Площадь S его поверхности равна:
A = L x l = 4 x 2 = 8 см².

Как рассчитать площадь прямоугольника, если мы знаем только одну сторону и диагональ

Можно определить площадь прямоугольника другим способом. Формула, которая была изложена ранее, не является единственным методом, который можно использовать. Действительно, вполне возможно сделать это по-другому. Для этого нам нужно будет, по крайней мере, измерить только одну сторону и необходимо знать длину диагонали. В этом случае мы делаем расчет, используя теорему Пифагора.

Что такое теорема Пифагора

Это формула, которая используется для определения длины третьей стороны прямоугольного треугольника, когда вы уже знаете значение двух других его сторон.

Обратите внимание, что прямоугольник состоит из двух прямоугольных треугольников. Действительно, диагональ представляет гипотенузу этого типа треугольника.

Теорема Пифагора

Кроме того, это также самая длинная сторона, которую можно найти на рисунке. Длина и ширина, с другой стороны, представляют две другие его стороны (скажем, смежные стороны). Это причина, почему можно использовать эту формулу для определения площади прямоугольника.

Теорема Пифагора основана на довольно простом уравнении, которое выглядит следующим образом: a² + b² = c². Где a и b используются для представления двух соседних сторон — катетов прямоугольного треугольника, а c представляет гипотенузу треугольника.

Чтобы полностью понять использование этой формулы, мы начнем с очень конкретного примера. Для этого предположим, что диагональ прямоугольника 10 см, а другая сторона 6 см. Если мы ссылаемся на формулу a² + b² = c², следовательно, сторона «a» составляет 6 см, а гипотенуза «c» — 10 см. Теперь нам нужно просто заменить буквенные значения числовыми значениями, которые у нас есть. Что дает нам:

a² + b² = c²
6² + b² = 10²
b² = 10² — 6²
b² = 100 — 36
b² = 64
b= 8
Мы получаем длину смежной стороны прямоугольника «b», которая равна 8 см. Теперь мы можем рассчитать площадь прямоугольника:

S = 8 см х 6 см
Следовательно, S = 48 см².

Источник

Как найти площадь фигуры

Обозначение площади

Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.

Если параметры фигуры переданы в разных единицах измерения длины, мы не сможем решить ни одну задачу. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

Круг — это множество точек на плоскости, ограниченных окружностью, удаленных от центра на равном радиусу расстоянии. Радиусом принято называть отрезок, соединяющий центр с любой точкой окружности.

S = &pi × d 2 : 4;, где d — это диаметр.

S = L 2 ​ : (4 × π), где L — это длина окружности.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Треугольник

Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, соединенных тремя отрезками. Эти три точки принято называть вершинами, а отрезки — сторонами. Рассчитать площадь треугольника можно несколькими способами по исходными данным, давайте их рассмотрим.

1. Если известна сторона и высота.

S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.

Основание может быть расположено иначе, например так:

При тупом угле высоту можно отразить на продолжение основания:

При прямом угле основанием и высотой будут его катеты:

2. Если известны две стороны и синус угла.

S = 0,5 × a × b * sinα, где a и b — две стороны, sinα — синус угла между ними.

3. Если есть радиус описанной окружности.

S = (a × b × с) : (4 × R), где a, b и с — стороны треугольника, а R — радиус описанной окружности.

4. Если есть радиус вписанной окружности.

S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.

Прямоугольник

Прямоугольник — это параллелограмм, у которого все углы прямые. Узнать площадь прямоугольника помогут следующие формулы:

S = a × b, где a, b — длина и ширина прямоугольника.

Диагональ — это отрезок, который соединяет вершины противоположных углов. Она есть во всех фигурах, число вершин которых больше трех.

S = 0,5 × d 2 × 𝑠𝑖𝑛(𝑎), где d — диагональ, α — угол между диагоналями.

Квадрат

Квадрат — это тот же прямоугольник, но при условии, что все его стороны равны. Найти его площадь легко:

S = d 2 : 2, где d — диагональ.

Трапеция

Трапеция — это четырехугольник, у которого две стороны параллельны и две не параллельны.

S = 0,5 × (a + b) × h, где a, b — два разных основания, h — высота трапеции.

Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны под прямым углом.

Параллелограмм и ромб

Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны.

Ромб — это параллелограмм, у которого все стороны равны.

Расскажем про общие формулы расчета площади этих фигур.

S = a × h, где a — сторона, h — высота.

S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. Для ромба формула примет вид S = a 2 × sinα.

Для ромба: S = 0,5 × (d₁ × d₂), где d₁, d₂ — две диагонали. Для параллелограмма: S = 0,5 × (d₁ × d₂) × sinβ, где β — угол между диагоналями.

Источник

Периметр и площадь прямоугольника

Прямоугольники и квадраты обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D

Определения:

Прямоугольник – это четырёхугольник, у которого все углы прямые.

Квадрат – это прямоугольник, у которого стороны равны. Его называют правильным четырёхугольником.

Периметр прямоугольника – это сумма длин всех сторон прямоугольника.

Формулы

Дан прямоугольник ABCD.

Периметр равен сумме длин сторон.

P_ABCD = AB + BC + CD + AD

Противоположные стороны прямоугольника равны.

P_ABCD = 2 * AB + 2 * BC = 2 * (AB + BC)

Следовательно, для того, чтобы высчитать периметр прямоугольника, нужно сложить длины двух сторон и умножить результат на 2.

У квадрата все стороны равны.

Поэтому, периметр квадрата равен:

Площадь прямоугольника равна произведению длины на ширину.

Определить площадь, периметр, объем, длину, диаметр, высоту и остальные геометрические величины поможет онлайн-калькулятор https://max-calc.ru.

На сайте вы сможете не только получить готовое решение, но и посмотреть всю необходимую справочную информацию.

Задачи:

1. Хозяин дачи решил построить забор вокруг участка. Какой длины получится забор, если участок имеет вид прямоугольника с шириной 15 метров и длиной 33 метра?

Для нахождения длины забора нужно посчитать периметр участка.

Воспользуемся формулай Р_{участка} = 2 * (длина + ширина).

Р _{участка} = 2 * (15 м + 33 м) = 96 м

Ответ: длина забора 96 метров.

2. Мама решила пришить на скатерть красивую тесьму. Сколько нужно купить тесьмы, если скатерть квадратная со стороной 150 сантиметров?

Так как скатерть квадратная, для определения длины тесьмы нужно найти периметр квадрата.

Р = 4 * 150 см = 600 см = 6 м

Ответ: нужно купить 6 метров тесьмы.

3. Известно, что банки краски хватает, чтобы покрасить 30 м 2 поверхности. Хватит ли одной банки краски, чтобы покрасить забор длиной 15 метров и высотой 2 метра?

Для решения необходимо найти площадь поверхности забора. Для этого длину умножаем на ширину.

S_забора = 15 м * 2 м = 30 м2.

Ответ: да, 1 банки краски хватит.

Задачи для самостоятельной работы:

1. Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.

2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.

Уважаемые читатели!

Все материалы с сайта можно скачивать абсолютно бесплатно. Все материалы проверены антивирусом и не содержат скрытых скриптов.

Материалы в архиве не помечены водяными знаками!

Если материал нарушает чьи-то авторские права, просьба написать нам по обратной связи, указав авторство материала. Мы обязуемся либо убрать материал, либо указать прямую ссылку на автора.

Сайт пополняется материалами на основе бесплатной работы авторов. Eсли вы хотите отблагодарить их за работу и поддержать наш проект, вы можете перевести любую, не обременительную для вас сумму на счет сайта.
Заранее Вам спасибо.

Источник

Математика. 5 класс

Конспект урока

Площадь прямоугольника. Единицы площади

Перечень рассматриваемых вопросов:

— понятие площади фигуры;

-единицы измерения площади;

— площадь прямоугольника, квадрата;

— приближенное измерение площади фигуры на клетчатой бумаге.

Прямоугольник – четырёхугольник, у которого все углы прямые (равны 90 градусам).

Квадрат – прямоугольник, у которого все стороны равны.

Площадь прямоугольника– число, которое показывает, сколько квадратных единиц содержится в прямоугольнике.

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений.// С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Сегодня мы начнём занятие с задачи. Представим, что две девочки пришли в магазин, чтобы купить в подарок подруге на день рождения коробку конфет. На витрине были разложены самые разные наборы сладостей. Девочки решили купить ту коробку, которая больше. А какая из них больше? Как это измерить? Можно сравнить коробки по длине и ширине или просто положить их друг на друга. Но одна коробка оказалась длиннее, а другая – шире. Какая же из них больше? Как это узнать?

Чтобы ответить на эти вопросы, мы поговорим о вычислении площади прямоугольника.

Для начала введём понятие площади фигуры.

За единицу измерения площадей принимают не только квадратный сантиметр, но и квадратный миллиметр, квадратный дециметр, квадратный метр.

Это площади квадратов, длины сторон которых равны одному миллиметру, одному дециметру и одному метру соответственно.

Далее покажем, что подразумевается под площадью прямоугольника.

Площадью прямоугольника называют число, которое показывает, сколько квадратных единиц содержится в прямоугольнике.

Называя величину площади, необходимо указывать единицу измерения.

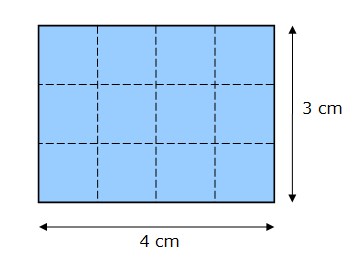
Найдём площадь прямоугольника ABCD, который имеет длину АВ = 6 см и ширину ВС = 7 см. Для этого разделим его на квадратные сантиметры. Сосчитаем, сколько квадратных сантиметров в нём содержится.

В прямоугольнике ABCD квадратный сантиметр содержится сорок два раза – значит, его площадь равна: S = 42 см 2 = 6 см · 7 см = АВ · ВС.

Поэтому можно ввести формулу для нахождения площади прямоугольника.

Чтобы найти площадь прямоугольника S, нужно умножить его длину a на ширину b.

Так как квадрат является прямоугольником, у которого все стороны равны, то его площадь можно вычислить как квадрат его стороны а.

Далее найдём соотношение между единицами измерения площадей.

Соответственно, 1 дм 2 = 10 2 см 2 = 100 см 2

1 м 2 = 10 2 дм 2 = 100 дм 2

Для измерения небольших площадей земельных участков используют специальную единицу измерения– ар, которая равна площади квадрата со стороной десять метров. В обиходе ар называют соткой, так как один ар– это сто квадратных метров.

1 ар = 10 2 м 2 = 100 м 2

Для обмера больших земельных территорий ввели единицу один гектар, которая соответствует площади квадрата со стороной сто метров.

1 га = 100 2 м 2 = 10000 м 2 = 100 а

Найдём площадь прямоугольника.

При измерении окажется, что стороны с недостатком приближенно равны трём и пяти сантиметрам. Значит, площадь прямоугольника больше, чем произведение этих сторон, то есть пятнадцати квадратных сантиметров.

S (с недостатком) = 3 · 5 = 15 см 2

Если взять стороны в приближении с избытком, то есть четыре и шесть сантиметров, то площадь будет меньше произведения сторон, а именно равна двадцати четырём квадратным сантиметрам.

S (с избытком) = 4 · 6 = 24 см 2

Таким образом, площадь этого прямоугольника варьируется от пятнадцати до двадцати четырёх квадратных сантиметров.

Отметим, что равные прямоугольники имеют равную площадь.

Сравним площади закрашенных квадратов, изображённых на рисунке.

Решение: если посмотреть внимательно на рисунок, то можно заметить, что все фигуры расположены в одинаковых квадратах со стороной 9 клеток, следовательно, площади этих квадратов одинаковы. На верхнем рисунке шесть фигур – два квадрата и четыре треугольника. На нижнем рисунке пять фигур – квадрат и четыре треугольника.

Далее внимательно посмотрим на треугольники – все они одинаковы, следовательно, их площади одинаковы. И, если из больших квадратов, в которых расположены наши фигуры, мы отнимем сумму площадей равных треугольников, получится, что площади оставшихся фигур (квадратов) верхней и нижней части равны.

Примеры заданий из Тренировочного модуля

№ 1. В квадрате все стороны равны 5 см. Чему равна площадь квадрата?

Решение: Для нахождения площади квадрата воспользуемся следующей формулой:

S = а 2 = 5см · 5 см = 25 см 2

№ 2. Найдите площадь фигуры.

Источник