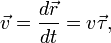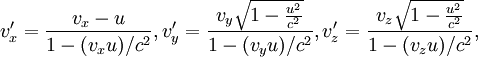что непосредственно приводит к повороту вектора скорости

Векторы ускорения и скорости. Ускорение и сила. Направления тангенциального и нормального ускорений

Как известно, любая физическая величина относится к одному из двух типов, она является либо скалярной, либо векторной. В данной статье рассмотрим такие кинематические характеристики как скорость и ускорение, а также покажем, куда направлены векторы ускорения и скорости.

Что такое скорость и ускорение?

Обе величины, названные в этом пункте, являются важными характеристиками любого вида движения, будь то перемещение тела по прямой линии или по криволинейной траектории.

Вам будет интересно: Дистанционное образование в России: история, статистика и преимущества

Скоростью называется быстрота изменения координат во времени. Математически эта величина равна производной по времени пройденного пути, то есть:

Здесь вектор l¯ направлен от начальной точки пути к конечной.

В свою очередь ускорение – это скорость, с которой изменяется во времени сама скорость. В виде формулы оно может быть записано так:

Очевидно, что взяв вторую производную от вектора перемещения l¯ по времени, мы также получим значение ускорения.

Поскольку скорость измеряется в метрах в секунду, то ускорение, согласно записанному выражению, измеряется в метрах в секунду в квадрате.

Куда направлены векторы ускорения и скорости?

Вектор скорости тела направлен в сторону движения всегда, независимо от того, замедляется или ускоряется тело, движется оно по прямой или по кривой. Если говорить геометрическими терминами, то вектор скорости направлен по касательной к точке траектории, в которой в данный момент находится тело.

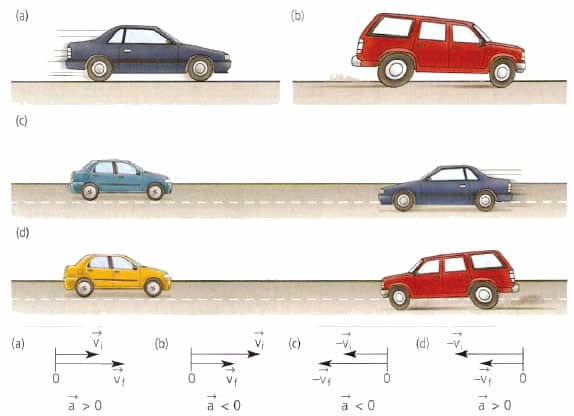
Вектор ускорения точки материальной или тела не имеет ничего общего со скоростью. Этот вектор направлен в сторону изменения скорости. Например, для прямолинейного движения величина a¯ может как совпадать по направлению с v¯, так и быть противоположной v¯.

Действующая на тело сила и ускорение

Мы выяснили, что вектор ускорения тела направлен в сторону изменения вектора скорости. Тем не менее не всегда можно легко определить, как меняется скорость в данной точке траектории. Более того, для определения изменения скорости необходимо выполнить операцию разности векторов. Чтобы избежать этих трудностей в определении направления вектора a¯, существует еще один способ быстро его узнать.

Ниже записан знаменитый и хорошо известный каждому школьнику закон Ньютона:

Формула показывает, что причиной возникновения ускорения у тел является действующая на них сила. Поскольку масса m является скаляром, то вектор силы F¯ и вектор ускорения a¯ направлены одинаково. Этот факт следует запомнить и применять на практике всегда, когда возникает необходимость в определении направления величины a¯.

Если на тело действуют несколько разных сил, тогда направление вектора ускорения будет равно результирующему вектору всех сил.

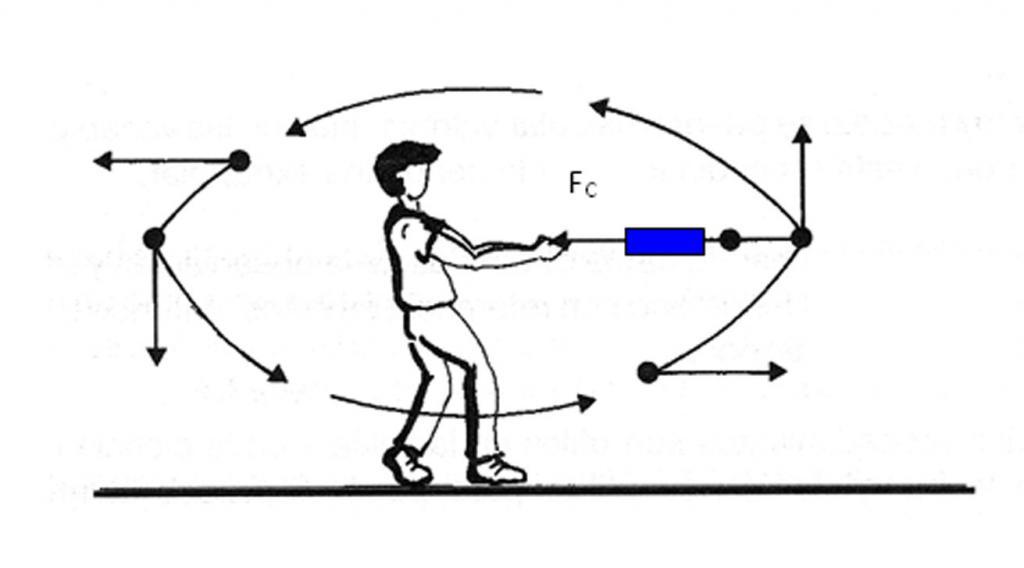
Движение по окружности и ускорение

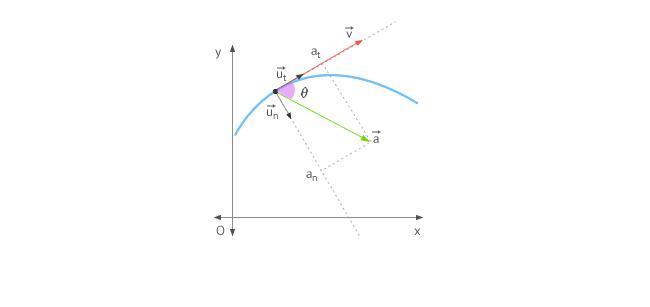
Когда тело перемещается по прямой линии, то ускорение направлено либо вперед, либо назад. В случае же движения по окружности ситуация усложняется тем, что вектор скорости постоянно меняет свое направление. В виду сказанного, полное ускорение определяется двумя его составляющими: тангенциальным и нормальным ускорениями.

Тангенциальное ускорение направлено точно так же, как вектор скорости, или против него. Иными словами, эта компонента ускорения направлена вдоль касательной к траектории. Ускорение тангенциальное описывает изменение модуля самой скорости.

Ускорение нормальное направлено вдоль нормали к данной точке траектории с учетом ее кривизны. В случае движения по окружности вектор этой компоненты указывает на центр, то есть нормальное ускорение направлено вдоль радиуса вращения. Эту компоненту часто называют центростремительной.

Полное ускорение представляет собой сумму названных компонент, поэтому его вектор может быть направлен произвольным образом по отношению к линии окружности.

Если тело совершает вращение без изменения линейной скорости, то существует отличная от нуля только нормальная компонента, поэтому вектор полного ускорения направлен к центру окружности. Заметим, что к этому центру также действует сила, удерживающая тело на его траектории. Например, сила гравитации Солнца удерживает нашу Землю и другие планеты на своих орбитах.

Источник

Вектор скорости

Ско́рость (часто обозначается , от англ. velocity или фр. vitesse ) — векторная величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта. Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.

В науке повсеместно используется также скорость в широком смысле, то есть как скорость изменения какой-либо величины (не обязательно радиус-вектора). Так, например, говорят об угловой скорости, скорости роста температуры, скорости химической реакции и т. д. Математически находится с помощью производной от данной величины (обычно по времени, либо от другого аргумента).

Содержание

Скорость тела в механике

Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора этой точки:

Здесь v — модуль скорости, — направленный вдоль скорости единичный вектор касательной к траектории в точке .

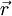
Говорят, что тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).

В общем случае, скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса величина скорости точек на ободе относительно дороги принимает значения от нуля (в точке касания с дорогой) до удвоенного значения скорости автомобиля (в точке, диаметрально противоположной точке касания). Распределение скоростей в твёрдом теле определяется с помощью кинематической формулы Эйлера.

Если скорость тела (как векторная величина) не меняется во времени, то движение тела — равномерное (ускорение равно нулю).

Полезно отличать понятие средней скорости перемещения от понятия средней скорости пути, равной отношению пройденного точкой пути ко времени, за которое этот путь был пройден. В отличие от скорости перемещения, средняя скорость пути — скаляр.

Мгновенная и средняя скорость

Преобразование скорости

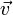
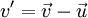
В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта S была равна , а скорость системы отсчёта S’ относительно системы отсчёта S равна , то скорость тела в при переходе в систему отсчёта S’ будет равна .

Для скоростей, близких к скорости света преобразования Галилея становятся несправедливы. При переходе из системы S в систему S’ необходимо использовать преобразования Лоренца для скоростей:

в предположении, что скорость направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.

Единицы измерения скорости

Соотношение между единицами скорости

См. также

Полезное

Смотреть что такое «Вектор скорости» в других словарях:

вектор скорости — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN velocity vector … Справочник технического переводчика

вектор скорости — greičio vektorius statusas T sritis fizika atitikmenys: angl. velocity vector vok. Geschwindigkeitsvektor, m rus. вектор скорости, m pranc. vecteur de vitesse, m; vecteur vitesse, m … Fizikos terminų žodynas

вектор скорости — greičio vektorius statusas T sritis Kūno kultūra ir sportas apibrėžtis Dydis, rodantis greičio statinę vertę (reikšmę) ir taško judėjimo kryptį. atitikmenys: angl. vector of velocity vok. Vektor der Geschwindigkeit, m rus. вектор скорости … Sporto terminų žodynas

вектор скорости ветра — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN wind vectorU … Справочник технического переводчика

вектор скорости вибрации — 3.4 вектор скорости вибрации : Вектор, содержащий шесть составляющих скорости вибрации (три линейные и три поворотные), направленных вдоль координатных осей x, y и z. Источник … Словарь-справочник терминов нормативно-технической документации

вектор скорости вибрации n-го виброизолятора — 3.13 вектор скорости вибрации n го виброизолятора : Вектор скорости вибрации n го виброизолятора (матрица столбец), содержащий шесть составляющих (три линейные и три поворотные), направленных вдоль координатных осей x, y и z. Источник … Словарь-справочник терминов нормативно-технической документации

вектор скорости вибрации в n-й точке — 3.6 вектор скорости вибрации в n й точке : Вектор в n й точке (матрица столбец), содержащий три линейные составляющие скорости вибрации, направленные вдоль координатных осей х, у и z соответственно. Источник … Словарь-справочник терминов нормативно-технической документации

вектор — 01.03.02 вектор [ vector] (1)1): Величина, представляемая значением, направлением, смысловым содержанием и началом. 1)Терминологические статьи 01.03.02 и 01.03.03 относятся к одному понятию. Источник … Словарь-справочник терминов нормативно-технической документации

ВЕКТОР — В физике и математике вектор это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент,… … Энциклопедия Кольера

Источник

Магия тензорной алгебры: Часть 6 — Кинематика свободного твердого тела. Природа угловой скорости

Введение

Что такое угловая скорость? Скалярная или векторная величина? На самом деле это не праздный вопрос.

Читая лекции по теоретической механике в университете, я, следуя традиционной методике изложения курса кинематики, вводил понятие угловой скорости в теме «Скорость точки тела при вращательном движении». И там угловая скорость впервые появляется как скалярная величина, со следующим определением.

Угловая скорость твердого тела — это первая производная от угла поворота тела по времени

А вот потом, при рассмотрении каноничной формулы Эйлера для скорости точки тела при вращении

Угловая скорость тела — это псевдовектор, направленный вдоль оси вращения тела в ту сторону, откуда вращение выглядит происходящим против часовой стрелки

Ещё одно частное определение, которое, во-первых, утверждает неподвижность оси вращения, во-вторых навязывает рассмотрение лишь правой системы координат. И наконец термин «псевдовектор» обычно объясняется студентам так: «Посмотрите, ведь мы показали, что омега — скалярная величина. А вектор мы вводим для того, чтобы выписать формулу Эйлера».

При рассмотрении сферического движения оказывается потом, что ось вращения меняет направление, угловое ускорение направлено по касательной к годографу угловой скорости и так далее. Неясности и вводные допущения множатся.

Учитывая уровень подготовки школьников, а так же вопиющую глупость, допускаемую в программах подготовки бакалавров, когда теормех начинается с первого (вдумайтесь!) семестра, такие постепенные вводные, на палках, веревках и желудях наверное оправданы.

Но мы с вами заглянем, что называется, «под капот» проблемы и, вооружившись аппаратом тензорного исчисления, выясним, что угловая скорость — это псевдовектор, порождаемый антисимметричным тензором второго ранга.

Думаю для затравки вполне достаточно, а поэтому — начнем!

1. Свободное движение твердого тела. Тензор поворота

Если движение, совершаемо телом не ограничено связями, то такое его движение называют свободным

Это — самый общий случай движения тела. Следующий рисунок иллюстрирует тот факт, что свободное движение тела можно представить как сумму двух движений: поступательного вместе с полюсом и сферического вокруг полюса.

Рис. 1. Обычная иллюстрация из курса теоретической механики: определение положения свободного твердого тела в пространстве.

Напомню, что речь идет об абсолютно твердом теле, то есть теле, расстояния между точками которого не изменяется с течением времени. Ещё можно сказать, что твердое тело представляет собой неизменяемую механическую систему.

Как видно из рисунка 1, обычной практикой является рассмотрение двух систем координат — одна считается неподвижной и называется базовой, другая жестко связанна с телом и поворачивается относительно базовой вместе с ним. Такую систему координат называют связанной.

Сначала я тоже хотел ограничиться декартовыми координатами. Но тогда бы мои читатели задали бы мне логичный вопрос — «а зачем тогда тут тензоры?». Поэтому, потратив четыре для в мучительных раздумьях и «нагуляв» окончательное решение пару часов назад, я решил замахнуться на «Вильяма, нашего, Шекспира» и изложить дальнейшие рассуждения в криволинейных координатах.

Рис. 2. Ориентация твердого тела в локальном базисе.

Пусть положение полюса задается вектором

Причем под этим вектором не следует понимать радиус-вектор, так как в криволинейных координатах такое понятие бессмысленно.

В точке O₁ задан локальный репер базовой системы координат, образованный тройкой векторов . С движущимся телом связан подвижный репер . Поворот связанного репера относительно базового можно задать линейным оператором. Получим этот оператор и исследуем его свойства

Рассмотрим некоторую точку M, принадлежащую телу. К ней из полюса можно провести вектор неподвижный относительно связанного репера. Его можно разложить по векторам этого репера

и по векторам базового репера

Каждый вектор связанного репера можно разложить через векторы базового репера

Подставляем (4) в (2) и сравниваем с (3)

Из (5) понятно, что компоненты вектора в базовой системе координат, пересчитываются через его компоненты в связанной системе путем применения линейного оператора

или в безиндексной форме

где столбцы матрицы

– контравариантные компоненты векторов связанного репера по отношению к базовому. Точка, как мы уже отмечали в прошлой статье, обозначает умножение тензоров с последующей сверткой по соседней паре индексов. Линейный оператор

действует на векторы таким образом, что поворачивает их относительно некоторой оси, не меняя длины и угла между векторами. Такое преобразование пространства называется ортогональным. Для того, чтобы таковое преобразование было возможным, оператор (7) должен обладать вполне определенными свойствами. Если длина векторов базиса и углы между ними не меняются, то это означает равенство всех попарных скалярных произведений векторов репера как в базовой, так и в связанной системах координат

Правая часть (8) — это локальный метрический тензор

Преобразование координат при повороте является тождественным для метрического тензора, то есть переводит метрический тензор сам в себя.

В выражении (10) нетрудно увидеть преобразование метрического тензора про смене системы координат, о котором мы подробно говорили в самой первой статье цикла

Стоп! Но мы же знаем, что матрицы поворота обычно ортогональны, то есть произведение матрицы поворота на её транспонированную дает единичную матрицу, иными словами, чтобы обратить матрицу поворота её достаточно транспонировать.

Но ортогональность свойственна матрицам поворота, преобразующим ортонормированный декартов базис. Здесь мы имеем дело с локальным базисом, при повороте которого должны сохранятся длины векторов и углы между ними. Если мы примем базис декартовым, то из (10) мы получим привычные свойства матрицы поворота, к примеру её ортогональность.

Для дальнейших вычислений нам потребуется знать, как будет выглядеть матрица обратного преобразования, то есть . Что же, посмотрим. Для этого умножим (10) слева на и справа на

откуда незамедлительно получаем

Выходит, что матрица обратного преобразования действительно получается из транспонированной матрицы преобразования, но с участием метрического тензора. Выражения (10) и (11) очень пригодятся нам, а пока сделаем некоторые выводы.

Закон свободного движения твердого тела можно выписать в криволинейных координатах в виде системы уравнений

При этом (12) — закон движения полюса, а (13) — закон сферического движения тела вокруг полюса. При этом (13) — тензор ранга (1,1), называемый тензором поворота.

2. Скорость точки тела при свободном движении. Угловая скорость выходит на сцену

Вычислим скорость точки M, положение которой в связанной системе координат задается постоянными, в силу твердости тела, криволинейными координатами

Из курса теоретической механики известна формула, определяющая скорость точки тела в данном движении

где — скорость полюса; — скорость точки вокруг полюса.

Так как все координаты, кроме (13) определены относительно базового репера, мы можем записать

Индекс в круглых скобках означает систему координат, в которой берутся компоненты (0 — базовая, 1 — связанная). Дифференцируем (15) по времени с учетом (13)

Перейдем в (16) к связанной системе координат, домножив (15) слева на

где — компонента оператора обратного преобразования .

Теперь сравним (17) и (14). В последнем слагаемом должно вылезти векторное произведение. Вспоминая определение векторного произведения через тензор Леви-Чивиты, данное во второй статье цикла, замечаем, что на выходе оно дает ковектор, поэтому в (17) перейдем к ковариантым компонентам, домножив это выражение на метрический тензор слева

Теперь представим себе, как выглядел бы ковектор скорости точки относительно плюса, записанный через вектор угловой скорости

Источник

Скорость, Вектор скорости и траектория, Сложение скоростей

Скорость

Средняя скорость частицы характеризует быстроту ее движения за конечный промежуток времени. Неограниченно уменьшая этот промежуток, мы придем к физической величине, характеризующей быстроту движения в данный момент времени. Такая величина называется мгновенной скоростью или просто скоростью:

обозначает математическую операцию перехода к пределу. Под этим символом записывается условие, при котором выполняется данный предельный переход; в рассматриваемом случае это стремление к нулю промежутка времени. При вычислении скорости по этому правилу мы убедимся, что уменьшение промежутка времени приводит к тому, что на некотором этапе получаемые очередные значения средней скорости будут все меньше и меньше отличаться друг от друга. Поэтому на практике при нахождении скорости можно остановиться на конечном значении, достаточно малом для получения требуемой точности значения скорости.

Вектор скорости и траектория.

Рассматриваемый предельный переход имеет ясный геометрический смысл. Поскольку вектор перемещения направлен по хорде, соединяющей две точки траектории, то при сближении этих точек, происходящем при, он принимает положение, соответствующее касательной к траектории в данной точке. Это значит, что вектор скорости направлен по касательной к траектории. Так будет в любой точке траектории (рис. 14). При прямолинейной траектории движения вектор скорости направлен вдоль этой прямой.

Скорость прохождения пути.

Аналогичным переходом определяется мгновенная скорость прохождения пути:

Сложение скоростей.

Иногда бывает удобно представить некоторое сложное движение как суперпозицию, т. е. наложение двух простых движений. В этом случае равенство (3) можно трактовать как правило разложения вектора скорости на составляющие.

По этой ссылке вы найдёте полный курс лекций по математике:

Задачи.

Переправа через реку. Скорость течения в реке с параллельными берегами всюду одинакова и равна. Ширина реки (рис. 15). Катер может плыть со скоростью относительно воды. На какое расстояние s снесет катер вниз по течению реки, если при переправе нос катера направить строго поперек берегов?

Эту задачу легко решить и не прибегая к сложению векторов скоростей.

2. Переправа поперек реки. Предположим, что теперь нам нужно переправиться на катере через ту же реку точно поперек, т. е. попасть в точку В, лежащую напротив начальной точки А (рис. 17). Как нужно направить нос катера при переправе? Сколько времени займет такая переправа?Решение. В рассматриваемом случае полная скорость v катера относительно берегов, равная векторной сумме скоростей должна быть направлена поперек реки.

Возможно вам будут полезны данные страницы:

3. Снос при быстром течении.

Предположим теперь, что скорость катера относительно воды меньше скорости течения: В таком случае переправа без сноса невозможна. Как следует направить нос катера при переправе, чтобы снос получился минимальным? На какое расстояние этом снесет катер? Решение. Полная скорость относительно берегов во всех рассматриваемых случаях дается формулой. Однако теперь нагляднее выполнить сложение векторов и по правилу треугольника (рис. 18) первым изображаем век гор для которого мы знаем модуль направление, а затем к его концу пристраиваем начало вектора известен только модуль, направление еще предстоит выбрать. Этот выбор нужно сделать так, вектор результирующей скорости как можно меньше отклонялся от направления поперек реки.

Рис. 19. Определение курса (направление вектора) переправы минимальным сносом 18. Сложение скоростей переправе Конец любом направлении должен лежать на окружности радиуса центр которой совпадает концом вектора. Эта окружность показана Так условию задачи то точка соответствующая началу лежит вне этой окружности.

наименьший угол тогда, когда он направлен касательной Следовательно, перпендикулярен вектору треугольник прямоугольный. Таким образом, направлять вверх течению под углом линии Синус этого угла дастся выражением Траектория направлена вдоль вектора, т.е. она перпендикулярна направлению, в котором смотрит катера. Это значит, своей траектории катер движется боком. другом берегу реки причалит точке, до найти из подобия треугольников. Модуль находится теореме Пифагора. результате получаем

4. Лодка тросе. Лодку подтягивают за привязанный носу трос, наматывая равномерно вращающийся барабан Барабан установлен высоком берегу. какой скоростью лодка тот момент, трос горизонтом? Трос выбирается барабаном скоростью.

Решение.

По мере приближения лодки к берегу угол а становится больше. Это значит, что cos а убывает и искомая скорость возрастает. Задача для самостоятельного решения Человек находится в поле на расстоянии от прямолинейного участка шоссе. Слева от себя он замечает движущийся по шоссе автомобиль. В каком направлении следует бежать к шоссе, чтобы выбежать на дорогу впереди автомобиля и как можно дальше от него? Скорость автомобиля и, скорость человека.

• Объясните, почему вектор скорости всегда направлен по касательной к траектории.

• В некоторых случаях траектория движения частицы может иметь изломы. Приведите примеры таких движений. Что можно сказать о направлении скорости в точках, где траектория имеет излом?

• В случае непрерывного механического движения вектор скорости не испытывает скачков ни по модулю, ни по направлению. Появление скачков скорости всегда связано с некоторой идеализацией реального процесса. Какие идеализации присутствовали в приведенных вами примерах траекторий с изломами?

Скорость как производная.

Вернемся к выражению (1) для мгновенной скорости. При движении частицы ее радиус-вектор г изменяется, т. е. является некоторой функцией времени:. Перемещение Дг за промежуток времени At представляет собой разность радиусов-векторов в моменты времени. Поэтому формулу (1) можно переписать в виде В математике такую величину называют производной от функции по времени Для нее используют следующие обозначения. Последнее обозначение (точка над буквой) характерно именно для производной по времени. Отметим, что в данном случае производная представляет собой вектор, так как получается в результате дифференцирования векторной функции по скалярному аргументу. Для модуля мгновенной скорости в соответствии справедливо выражение в начале статьи.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник