что необходимо подавать на вход нейронной сети чтобы закодировать предложение
Нейросети для чайников. Начало
Так получилось, что в университете тема нейросетей успешно прошла мимо моей специальности, несмотря на огромный интерес с моей стороны. Попытки самообразования несколько раз разбивались невежественным челом о несокрушимые стены цитадели науки в облике непонятных «с наскока» терминов и путанных объяснений сухим языком вузовских учебников.
В данной статье (цикле статей?) я попытаюсь осветить тему нейросетей с точки зрения человека непосвященного, простым языком, на простых примерах, раскладывая все по полочкам, а не «массив нейронов образует перцептрон, работающий по известной, зарекомендовавшей себя схеме».
Заинтересовавшихся прошу под кат.
Для чего же нужны нейросети?
Нейросеть – это обучаемая система. Она действует не только в соответствии с заданным алгоритмом и формулами, но и на основании прошлого опыта. Этакий ребенок, который с каждым разом складывает пазл, делая все меньше ошибок.
И, как принято писать у модных авторов – нейросеть состоит из нейронов.
Тут нужно сделать остановку и разобраться.
Договоримся, что нейрон – это просто некая воображаемая чёрная коробка, у которой кучка входных отверстий и одно выходное.
Причем как входящая, так и исходящая информация может быть аналоговой (чаще всего так и будет).
Как выходной сигнал формируется из кучи входных – определяет внутренний алгоритм нейрона.
Для примера напишем небольшую программу, которая будет распознавать простые изображения, скажем, буквы русского языка на растровых изображениях.
Условимся, что в исходном состоянии наша система будет иметь «пустую» память, т.е. этакий новорожденный мозг, готовый к бою.
Для того чтобы заставить его корректно работать, нам нужно будет потратить время на обучение.
Уворачиваясь от летящих в меня помидоров, скажу, что писать будем на Delphi (на момент написания статьи была под рукой). Если возникнет необходимость – помогу перевести пример на другие языки.
Также прошу легкомысленно отнестись к качеству кода – программа писалась за час, просто чтобы разобраться с темой, для серьезных задач такой код вряд ли применим.
Итак, исходя из поставленной задачи — сколько вариантов выхода может быть? Правильно, столько, сколько букв мы будем уметь определять. В алфавите их пока только 33, на том и остановимся.
Далее, определимся со входными данными.Чтобы слишком не заморачиватсья – будем подавать на вход битовый массив 30х30 в виде растрового изображения:
В итоге – нужно создать 33 нейрона, у каждого из которых будет 30х30=900 входов.
Создадим класс для нашего нейрона:
Создадим массив нейронов, по количеству букв:
Теперь вопрос – где мы будем хранить «память» нейросети, когда программа не работает?
Чтобы не углубляться в INI или, не дай бог, базы данных, я решил хранить их в тех же растровых изображениях 30х30.
Вот например, память нейрона «К» после прогона программы по разным шрифтам:
Как видно, самые насыщенные области соответствуют наиболее часто встречаемым пикселям.
Будем загружать «память» в каждый нейрон при его создании:
В начале работы необученной программы, память каждого нейрона будет белым пятном 30х30.
Распознавать нейрон будет так:
— Берем 1й пиксель
— Сравниваем его с 1м пикселем в памяти (там лежит значение 0..255)
— Сравниваем разницу с неким порогом
— Если разница меньше порога – считаем, что в данной точке буква похожа на лежащую в памяти, добавляем +1 к весу нейрона.
И так по всем пикселям.
Вес нейрона – это некоторое число (в теории до 900), которое определяется степенью сходства обработанной информации с хранимой в памяти.
В конце распознавания у нас будет набор нейронов, каждый из которых считает, что он прав на сколько-то процентов. Эти проценты – и есть вес нейрона. Чем больше вес, тем вероятнее, что именно этот нейрон прав.
Теперь будем скармливать программе произвольное изображение и пробегать каждым нейроном по нему:
Как только закончится цикл для последнего нейрона – будем выбирать из всех тот, у которого вес больше:
Именно по вот этому значению max_n, программа и скажет нам, что, по её мнению, мы ей подсунули.
По началу это будет не всегда верно, поэтому нужно сделать алгоритм обучения.
Само обновление памяти будем делать так:
Т.е. если данная точка в памяти нейрона отсутствует, но учитель говорит, что она есть в этой букве – мы её запоминаем, но не полностью, а только наполовину. С дальнейшим обучением, степень влияния данного урока будет увеличиваться.
Вот несколько итераций для буквы Г:
На этом наша программа готова.
Обучение
Начнем обучение.
Открываем изображения букв и терпеливо указываем программе на её ошибки:
Через некоторое время программа начнет стабильно определять даже не знакомые ей ранее буквы:
Заключение
Программа представляет собой один сплошной недостаток – наша нейросеть очень глупа, она не защищена от ошибок пользователя при обучении и алгоритмы распознавания просты как палка.
Зато она дает базовые знания о функционировании нейросетей.
Если данная статья заинтересует уважаемых хабравчан, то я продолжу цикл, постепенно усложняя систему, вводя дополнительные связи и веса, рассмотрю какую-нибудь из популярных архитектур нейросетей и т.д.
Поиздеваться над нашим свежерожденный интеллектом вы можете, скачав программу вместе с исходниками тут.
За сим откланяюсь, спасибо за чтение.
UPD: У нас получилась заготовка для нейросети. Пока что это ещё ей не является, но в следующей статье мы постараемся сделать из неё полноценную нейросеть.
Спасибо Shultc за замечание.
Основы нейросетей в 100 строках кода (часть 1)
В трёх частях этой статьи мы:
Вступление
Сегодня восхитительное время для всех увлечённых тайнами и возможностями глубокого обучения.
Многие герои глубокого обучения делятся своим опытом в своих видео и статьях. Это Jeremy Howard из fast.ai, Andrew Ng из Coursera, Andrej Karpathy, Yann Lecun, Ian Goodfellow, Yoshua Bengio, Lex Fridman, Geoffrey Hinton, Jürgen Schmidhuber и многие другие
Большинство из них рекомендует одну важную идею — постигать основные принципы глубокого обучения, реализуя их самостоятельно.
Сегодня в нашем распоряжении есть прекрасные мощные библиотеки: Tenserflow, PyTorch, Fast.ai, Keras, Mxnett, Nctk, DL4J и многие другие. Но используя только их, вы можете упустить кое-что важное — возможность глубже поразмышлять о самых важных моментах процесса обучения.
Программирование сети своими силами столкнет вас лицом к лицу с ключевыми проблемами и препятствиями в этом увлекательном приключении и познакомит со скрытыми чудесами глубокого обучения.
Мы рассмотрим все модные архитектуры и последние разработки в глубоком обучении — свёрточные сети, рекуррентные сети, генеративно-состязательные сети и многое другие. Что действительно интересно, практически за каждым успехом в этой области нам будут встречаться одни и те же старые друзья: обратное распространение и градиентный спуск.
Движение по ландшафту функции потерь. Значения масштабированы для наглядности.
Обе эти концепции дают практически безграничные возможности — и далее вы сможете работать с вышеперечисленными библиотеками более свободно и уверенно и будете готовы самостоятельно размышлять над тем, как их улучшить.
В поисках загадочной функции
Многое из происходящего во Вселенной может быть выражено с помощью функции. Функция — это математическая конструкция, которая берет какие-то данные на вход и вычисляет какие-то данные на выход. Причина и следствие. Вход и выход.
Когда мы смотрим на мир, мы видим информацию, мы видим данные. И многое можем из них узнать.
Есть много видов обучения, которое можно производить с этими данными. Давайте взглянем на 3 наиболее распространенных:
Итак, у нас есть некоторые данные, мы их передаём на вход функции, и также есть выходные данные, которые им соответствуют. И мы хотим понять, как наша загадочная функция связывает выходные данные с входными.
Дело в том, что когда связь между ними достаточно сложна, найти эту функцию становится действительно сложно. И здесь в дело вступают нейронные сети и глубокое обучение.
В своей основе нейронная сеть соединяет ваши входные данные с желаемыми выходными данными через серию промежуточных «весов». Эти веса — просто числа.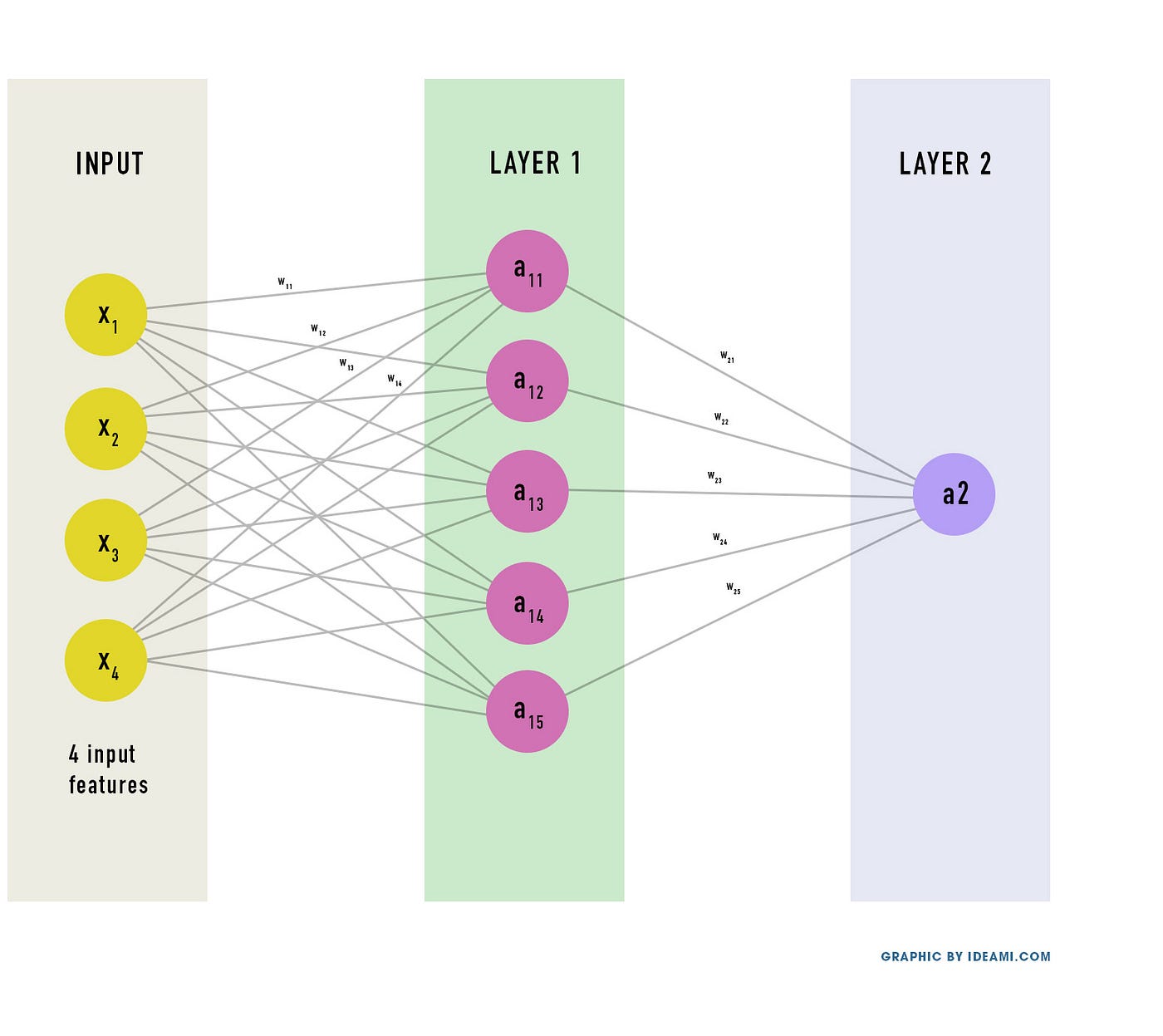 
С помощью своей архитектуры и алгоритмов оптимизации, которые мы вскоре рассмотрим, нейронные сети становятся универсальными аппроксиматорами. В конечном итоге они могут вычислить любую функцию, соединяющую входы с выходами (при условии, что у нас правильная архитектура и параметры — более подробно см. универсальная теорема аппроксимации — математическая теория нейросетей).
И лучший способ разобраться в нейронных сетях это… создать собственную. Причём с нуля, используя Python. Именно этим мы и займёмся, и в процессе рассмотрим множество интересных тем и концепций.
Лучший способ разобраться в нейронных сетях это… создать собственную
Ниже можно увидеть сеть, которую мы будем строить. У неё 2 слоя (не считаем входной слой).
У каждого нейрона сети есть вес (и смещение, но об этом позже). Эти веса — просто числа, которые в начале обучения обычно заполняются случайными значениями.
Нейронная сеть производит некоторые вычисления с входными данными, используя веса. Их результат проходит через сеть до тех пор, пока не получится окончательный результат на выходе.
Результат этих вычислений выражается функцией, которая как бы переводит входы в выходы.
Теперь мы хотим, чтобы сеть узнала наилучшие значения этих весов. Поскольку сеть выполняет вычисления с этими весами на разных слоях, она может аппроксимировать различные виды функции.
Теперь давайте лучше поймем эту загадочную функцию, которую мы ищем. Для этого очень важно разобраться с обозначениями всех переменных, вовлечённых в нашу миссию.
Сеть вычисляет взвешенную сумму:
А теперь добавим дополнительное слагаемое к этому произведению — коэффициент смещения: W⋅X + b.
Коэффициент смещения делает нашу сеть более гибкой. Он позволяет «сдвигать» линейные вычисления нейронов, увеличивая тем самым потенциал сети изучать эти загадочных функций быстрее.
А теперь вспомним, что нейронная сеть может иметь много слоев. В нашем примере их 2, но могло бы быть 20 или 200.
Поэтому мы будем помечать числами, к какому слою какое выражение относится. Линейное уравнение, которые определяет вычисления нашего скрытого слоя (слоя 1): W1⋅X + b1.
Давайте дадим обозначение результату этого вычисления:
Следовательно, Z1 = W1⋅X + b1.
Обратите внимание, что это нужно вычислить для каждого нейрона каждого слоя. В нашей сети мы будем использовать векторную реализацию — то есть, будем использовать матрицы для объединения всех вычислений в одну операцию.
Для этой статьи не так важно понимать матрицы на действительно хорошем уровне, но если вы хотите освежить свои знания, можно посмотреть замечательные видео от «3Blue1Brown» и его курс «Сущность линейной алгебры» (примечание: мы переводим этот курс, можно подписаться на канал или в вк).
Пока неплохо. А теперь давайте представим сеть со множеством слоёв. Каждый слой производит подобное линейное вычисление. Когда вы объедините все линейные вычисления вместе, сеть сможет вычислять сложные функции.
Однако, есть небольшая проблема…
Слишком линейно, слишком скучно
Мир сложен. Мир — это беспорядок. В жизни взаимосвязь между входными и выходными данными обычно не бывает линейна. Она склонна быть запутанной, нелинейной.
Сложные функции часто нелинейны. И нейронной сети трудно вычислить нелинейное поведение, если её архитектура создана для линейных вычислений. Поэтому нейронные сети добавляют в конец каждого слоя кое-что ещё: функцию активации.
Функция активации — это нелинейная функция, которая вносит нелинейные изменения в выход (результат вычислений) слоя. Она гарантирует, что сеть способна вычислить всевозможные сложные функции, включая очень сильно нелинейные.
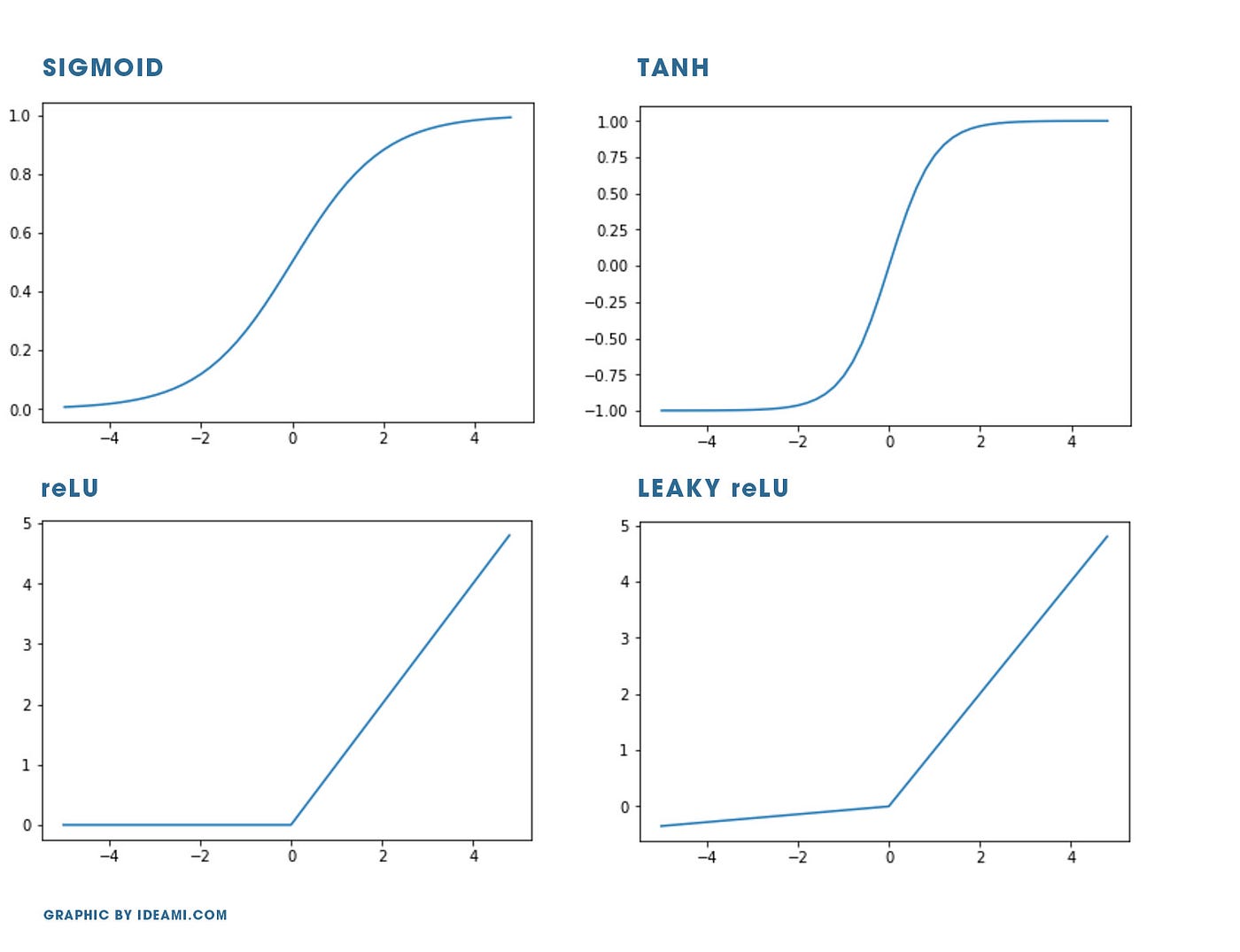
Существует множество различных видов функции активации. Кратко рассмотрим 4 основных.
Но сперва, чтобы хорошо их понять, нужно познакомиться с понятием «градиент» (позже мы рассмотрим его подробнее). Градиент функции в точке также называется её производной и выражает скорость изменения значения функции в этой точке.
В каком направлении и как сильно изменяется значение функции в ответ на изменения входной переменной?
Когда градиенты (производные) становятся слишком маленькими, а функция становится более гладкой, это значит, что мы имеем дело с исчезающим градиентом. Как мы позже узнаем, алгоритм обратного распространения, широко используемый в глубоком обучении, настраивает значения весов сети, используя градиент — с его помощью можно понять, как каждый из параметров влияет на выход сети (ведёт ли его изменение к увеличению или уменьшению выхода?).
Исчезающий градиент — это действительно проблема, потому что если градиент в точке становится слишком маленьким или равным нулю, становится очень трудно определить, в каком направлении изменяется выход системы.
Можно также говорить об обратной проблеме: взрывающемся градиенте. Когда значение градиента становится слишком большим, сеть становится очень нестабильной.
У каждой функции активации есть свои плюсы, но все они могут страдать от исчезающих и взрывающихся градиентов.
Давайте быстренько познакомимся с самыми популярными функциями активации.
Sigmoid
Tanh (гиперболический тангенс)
ReLU (rectified linear unit)
Softmax
В этой статье мы будем использовать Sigmoid на последнем слое и ReLU на скрытом слое.
Окей, мы разобрались с функциями активации, давайте дадим им имена!
Значит, вычисления, которые мы производим на скрытом слое, примут вид:
A1 = ReLU(Z1)
и Z1=W1⋅X + b1
А вычисления на выходном слое примут вид:
A2 = Sigmoid(Z2)
и Z2=W2⋅A1 + b2
Обратите внимание, что мы используем A1 в уравнении для Z2, потому что входным сигналом для нейронов 2 слоя является выходной сигнал нейронов скрытого (предыдущего) слоя.
Также обратите внимание, что Yh = A2. Выход второго слоя — это конечный выход сети.
Это всё. Теперь, если мы объединим все эти вычисления, мы получим полную формулу нашей сети:
Yh = A2 = Sigmoid(W2 ⋅ ReLU ⋅ (W1 ⋅ X+ b1) + b2)
Теперь точно всё. Это всё вычисления, которые производит наша двухслойная нейронная сеть.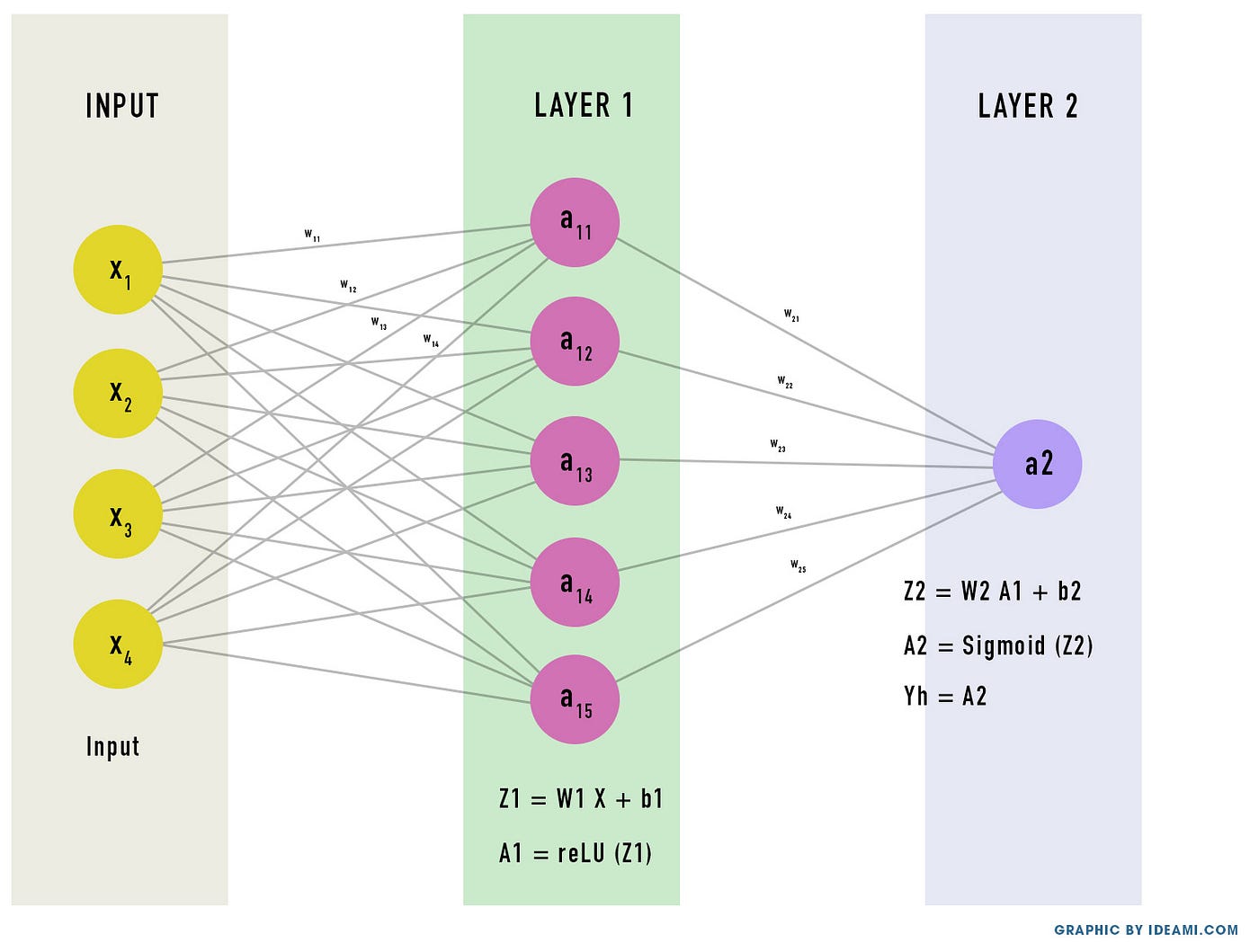
То есть, нейронная сеть — цепочка функций, линейных и нелинейных, которые вместе образуют сложную функцию — ту самую загадочную функцию, которая свяжет ваши входные данные с желаемым результатом.
Обратите внимание на переменные W и b в нашей сложной функции. Именно в нахождении их оптимальных значений и заключается обучение. Каким-то образом сеть должна узнать корректные (наиболее оптимальные) значения этих переменные, чтобы правильно вычислить значение функции.
Мы будем учиться находить оптимальные значения для W1, b1, W2, b2. Но перед тем, как мы приступим к тренировке сети, нам нужно инициализировать эти переменные начальными значениями.
Как правильно инициализировать веса и смещения — целая отдельная тема. Для начала мы инициализируем их случайными значениями.
На этом этапе мы уже можем приступить к написанию кода нашей сети. В следующей части мы создадим класс на Python, который будет инициализировать основные параметры сети, и посмотрим, как её тренировать.
Перевод: Титов Дмитрий
Перевод, редактура, корректура, вёрстка: Дмитрий Мирошниченко Keyten
Sciberia — это открытый проект, где совместными усилиями участники переводят с английского языка актуальные образовательные и научно-популярные материалы известных мировых институтов и экспертов из различных областей. Участником проекта может стать любой, кто хочет создавать переводы в команде.
Если у вас есть желание помочь с переводами, пишите Станиславу (телеграм: @pieceofchaos).
Нейронные сети для начинающих. Часть 2
Добро пожаловать во вторую часть руководства по нейронным сетям. Сразу хочу принести извинения всем кто ждал вторую часть намного раньше. По определенным причинам мне пришлось отложить ее написание. На самом деле я не ожидал, что у первой статьи будет такой спрос и что так много людей заинтересует данная тема. Взяв во внимание ваши комментарии, я постараюсь предоставить вам как можно больше информации и в то же время сохранить максимально понятный способ ее изложения. В данной статье, я буду рассказывать о способах обучения/тренировки нейросетей (в частности метод обратного распространения) и если вы, по каким-либо причинам, еще не прочитали первую часть, настоятельно рекомендую начать с нее. В процессе написания этой статьи, я хотел также рассказать о других видах нейросетей и методах тренировки, однако, начав писать про них, я понял что это пойдет вразрез с моим методом изложения. Я понимаю, что вам не терпится получить как можно больше информации, однако эти темы очень обширны и требуют детального анализа, а моей основной задачей является не написать очередную статью с поверхностным объяснением, а донести до вас каждый аспект затронутой темы и сделать статью максимально легкой в освоении. Спешу расстроить любителей “покодить”, так как я все еще не буду прибегать к использованию языка программирования и буду объяснять все “на пальцах”. Достаточно вступления, давайте теперь продолжим изучение нейросетей.
Что такое нейрон смещения?
Перед тем как начать нашу основную тему, мы должны ввести понятие еще одного вида нейронов — нейрон смещения. Нейрон смещения или bias нейрон — это третий вид нейронов, используемый в большинстве нейросетей. Особенность этого типа нейронов заключается в том, что его вход и выход всегда равняются 1 и они никогда не имеют входных синапсов. Нейроны смещения могут, либо присутствовать в нейронной сети по одному на слое, либо полностью отсутствовать, 50/50 быть не может (красным на схеме обозначены веса и нейроны которые размещать нельзя). Соединения у нейронов смещения такие же, как у обычных нейронов — со всеми нейронами следующего уровня, за исключением того, что синапсов между двумя bias нейронами быть не может. Следовательно, их можно размещать на входном слое и всех скрытых слоях, но никак не на выходном слое, так как им попросту не с чем будет формировать связь.
Для чего нужен нейрон смещения?
Нейрон смещения нужен для того, чтобы иметь возможность получать выходной результат, путем сдвига графика функции активации вправо или влево. Если это звучит запутанно, давайте рассмотрим простой пример, где есть один входной нейрон и один выходной нейрон. Тогда можно установить, что выход O2 будет равен входу H1, умноженному на его вес, и пропущенному через функцию активации (формула на фото слева). В нашем конкретном случае, будем использовать сигмоид.
Из школьного курса математики, мы знаем, что если взять функцию y = ax+b и менять у нее значения “а”, то будет изменяться наклон функции (цвета линий на графике слева), а если менять “b”, то мы будем смещать функцию вправо или влево (цвета линий на графике справа). Так вот “а” — это вес H1, а “b” — это вес нейрона смещения B1. Это грубый пример, но примерно так все и работает (если вы посмотрите на функцию активации справа на изображении, то заметите очень сильное сходство между формулами). То есть, когда в ходе обучения, мы регулируем веса скрытых и выходных нейронов, мы меняем наклон функции активации. Однако, регулирование веса нейронов смещения может дать нам возможность сдвинуть функцию активации по оси X и захватить новые участки. Иными словами, если точка, отвечающая за ваше решение, будет находиться, как показано на графике слева, то ваша НС никогда не сможет решить задачу без использования нейронов смещения. Поэтому, вы редко встретите нейронные сети без нейронов смещения.
Также нейроны смещения помогают в том случае, когда все входные нейроны получают на вход 0 и независимо от того какие у них веса, они все передадут на следующий слой 0, но не в случае присутствия нейрона смещения. Наличие или отсутствие нейронов смещения — это гиперпараметр (об этом чуть позже). Одним словом, вы сами должны решить, нужно ли вам использовать нейроны смещения или нет, прогнав НС с нейронами смешения и без них и сравнив результаты.
ВАЖНО знать, что иногда на схемах не обозначают нейроны смещения, а просто учитывают их веса при вычислении входного значения например:
input = H1*w1+H2*w2+b3
b3 = bias*w3
Так как его выход всегда равен 1, то можно просто представить что у нас есть дополнительный синапс с весом и прибавить к сумме этот вес без упоминания самого нейрона.
Как сделать чтобы НС давала правильные ответы?
Ответ прост — нужно ее обучать. Однако, насколько бы прост не был ответ, его реализация в плане простоты, оставляет желать лучшего. Существует несколько методов обучения НС и я выделю 3, на мой взгляд, самых интересных:
Что такое градиентный спуск?
Это способ нахождения локального минимума или максимума функции с помощью движения вдоль градиента. Если вы поймете суть градиентного спуска, то у вас не должно возникнуть никаких вопросов во время использования метода обратного распространения. Для начала, давайте разберемся, что такое градиент и где он присутствует в нашей НС. Давайте построим график, где по оси х будут значения веса нейрона(w) а по оси у — ошибка соответствующая этому весу(e).
Посмотрев на этот график, мы поймем, что график функция f(w) является зависимостью ошибки от выбранного веса. На этом графике нас интересует глобальный минимум — точка (w2,e2) или, иными словами, то место где график подходит ближе всего к оси х. Эта точка будет означать, что выбрав вес w2 мы получим самую маленькую ошибку — e2 и как следствие, самый лучший результат из всех возможных. Найти же эту точку нам поможет метод градиентного спуска (желтым на графике обозначен градиент). Соответственно у каждого веса в нейросети будет свой график и градиент и у каждого надо найти глобальный минимум.
Так что же такое, этот градиент? Градиент — это вектор который определяет крутизну склона и указывает его направление относительно какой либо из точек на поверхности или графике. Чтобы найти градиент нужно взять производную от графика по данной точке (как это и показано на графике). Двигаясь по направлению этого градиента мы будем плавно скатываться в низину. Теперь представим что ошибка — это лыжник, а график функции — гора. Соответственно, если ошибка равна 100%, то лыжник находиться на самой вершине горы и если ошибка 0% то в низине. Как все лыжники, ошибка стремится как можно быстрее спуститься вниз и уменьшить свое значение. В конечном случае у нас должен получиться следующий результат:
Представьте что лыжника забрасывают, с помощью вертолета, на гору. На сколько высоко или низко зависит от случая (аналогично тому, как в нейронной сети при инициализации веса расставляются в случайном порядке). Допустим ошибка равна 90% и это наша точка отсчета. Теперь лыжнику нужно спуститься вниз, с помощью градиента. На пути вниз, в каждой точке мы будем вычислять градиент, что будет показывать нам направление спуска и при изменении наклона, корректировать его. Если склон будет прямым, то после n-ого количества таких действий мы доберемся до низины. Но в большинстве случаев склон (график функции) будет волнистый и наш лыжник столкнется с очень серьезной проблемой — локальный минимум. Я думаю все знают, что такое локальный и глобальный минимум функции, для освежения памяти вот пример. Попадание в локальный минимум чревато тем, что наш лыжник навсегда останется в этой низине и никогда не скатиться с горы, следовательно мы никогда не сможем получить правильный ответ. Но мы можем избежать этого, снарядив нашего лыжника реактивным ранцем под названием момент (momentum). Вот краткая иллюстрация момента:
Как вы уже наверное догадались, этот ранец придаст лыжнику необходимое ускорение чтобы преодолеть холм, удерживающий нас в локальном минимуме, однако здесь есть одно НО. Представим что мы установили определенное значение параметру момент и без труда смогли преодолеть все локальные минимумы, и добраться до глобального минимума. Так как мы не можем просто отключить реактивный ранец, то мы можем проскочить глобальный минимум, если рядом с ним есть еще низины. В конечном случае это не так важно, так как рано или поздно мы все равно вернемся обратно в глобальный минимум, но стоит помнить, что чем больше момент, тем больше будет размах с которым лыжник будет кататься по низинам. Вместе с моментом в методе обратного распространения также используется такой параметр как скорость обучения (learning rate). Как наверняка многие подумают, чем больше скорость обучения, тем быстрее мы обучим нейросеть. Нет. Скорость обучения, также как и момент, является гиперпараметром — величина которая подбирается путем проб и ошибок. Скорость обучения можно напрямую связать со скоростью лыжника и можно с уверенностью сказать — тише едешь дальше будешь. Однако здесь тоже есть определенные аспекты, так как если мы совсем не дадим лыжнику скорости то он вообще никуда не поедет, а если дадим маленькую скорость то время пути может растянуться на очень и очень большой период времени. Что же тогда произойдет если мы дадим слишком большую скорость?
Как видите, ничего хорошего. Лыжник начнет скатываться по неправильному пути и возможно даже в другом направлении, что как вы понимаете только отдалит нас от нахождения правильного ответа. Поэтому во всех этих параметрах нужно находить золотую середину чтобы избежать не сходимости НС (об этом чуть позже).
Что такое Метод Обратного Распространения (МОР)?
А теперь давайте подробно разберем каждый этап. Если вы помните то в предыдущей статье мы считали выход НС. По другому это называется передача вперед (Forward pass), то есть мы последовательно передаем информацию от входных нейронов к выходным. После чего мы вычисляем ошибку и основываясь на ней делаем обратную передачу, которая заключается в том, чтобы последовательно менять веса нейронной сети, начиная с весов выходного нейрона. Значение весов будут меняться в ту сторону, которая даст нам наилучший результат. В моих вычисления я буду пользоваться методом нахождения дельты, так как это наиболее простой и понятный способ. Также я буду использовать стохастический метод обновления весов (об этом чуть позже).
Теперь давайте продолжим с того места, где мы закончили вычисления в предыдущей статье.
H1input = 1*0.45+0*-0.12=0.45
H1output = sigmoid(0.45)=0.61
H2input = 1*0.78+0*0.13=0.78
H2output = sigmoid(0.78)=0.69
O1input = 0.61*1.5+0.69*-2.3=-0.672
O1output = sigmoid(-0.672)=0.33
Результат — 0.33, ошибка — 45%.
Так как мы уже подсчитали результат НС и ее ошибку, то мы можем сразу приступить к МОРу. Как я уже упоминал ранее, алгоритм всегда начинается с выходного нейрона. В таком случае давайте посчитаем для него значение δ (дельта) по формуле 1.
Так как у выходного нейрона нет исходящих синапсов, то мы будем пользоваться первой формулой (δ output), следственно для скрытых нейронов мы уже будем брать вторую формулу (δ hidden). Тут все достаточно просто: считаем разницу между желаемым и полученным результатом и умножаем на производную функции активации от входного значения данного нейрона. Прежде чем приступить к вычислениям я хочу обратить ваше внимание на производную. Во первых как это уже наверное стало понятно, с МОР нужно использовать только те функции активации, которые могут быть дифференцированы. Во вторых чтобы не делать лишних вычислений, формулу производной можно заменить на более дружелюбную и простую формула вида:
Таким образом наши вычисления для точки O1 будут выглядеть следующим образом.
O1output = 0.33
O1ideal = 1
Error = 0.45
δO1 = (1 — 0.33) * ( (1 — 0.33) * 0.33 ) = 0.148
На этом вычисления для нейрона O1 закончены. Запомните, что после подсчета дельты нейрона мы обязаны сразу обновить веса всех исходящих синапсов этого нейрона. Так как в случае с O1 их нет, мы переходим к нейронам скрытого уровня и делаем тоже самое за исключение того, что формула подсчета дельты у нас теперь вторая и ее суть заключается в том, чтобы умножить производную функции активации от входного значения на сумму произведений всех исходящих весов и дельты нейрона с которой этот синапс связан. Но почему формулы разные? Дело в том что вся суть МОР заключается в том чтобы распространить ошибку выходных нейронов на все веса НС. Ошибку можно вычислить только на выходном уровне, как мы это уже сделали, также мы вычислили дельту в которой уже есть эта ошибка. Следственно теперь мы будем вместо ошибки использовать дельту которая будет передаваться от нейрона к нейрону. В таком случае давайте найдем дельту для H1:
H1output = 0.61
w5 = 1.5
δO1 = 0.148
δH1 = ( (1 — 0.61) * 0.61 ) * ( 1.5 * 0.148 ) = 0.053
Теперь нам нужно найти градиент для каждого исходящего синапса. Здесь обычно вставляют 3 этажную дробь с кучей производных и прочим математическим адом, но в этом и вся прелесть использования метода подсчета дельт, потому что в конечном счете ваша формула нахождения градиента будет выглядеть вот так:
Здесь точка A это точка в начале синапса, а точка B на конце синапса. Таким образом мы можем подсчитать градиент w5 следующим образом:
H1output = 0.61
δO1 = 0.148
GRADw5 = 0.61 * 0.148 = 0.09
Сейчас у нас есть все необходимые данные чтобы обновить вес w5 и мы сделаем это благодаря функции МОР которая рассчитывает величину на которую нужно изменить тот или иной вес и выглядит она следующим образом:
Настоятельно рекомендую вам не игнорировать вторую часть выражения и использовать момент так как это вам позволит избежать проблем с локальным минимумом.
Здесь мы видим 2 константы о которых мы уже говорили, когда рассматривали алгоритм градиентного спуска: E (эпсилон) — скорость обучения, α (альфа) — момент. Переводя формулу в слова получим: изменение веса синапса равно коэффициенту скорости обучения, умноженному на градиент этого веса, прибавить момент умноженный на предыдущее изменение этого веса (на 1-ой итерации равно 0). В таком случае давайте посчитаем изменение веса w5 и обновим его значение прибавив к нему Δw5.
E = 0.7
Α = 0.3
w5 = 1.5
GRADw5 = 0.09
Δw5(i-1) = 0
Δw5 = 0.7 * 0.09 + 0 * 0.3 = 0.063
w5 = w5 + Δw5 = 1.563
Таким образом после применения алгоритма наш вес увеличился на 0.063. Теперь предлагаю сделать вам тоже самое для H2.
GRADw6 = 0.69 * 0.148 = 0.1
Δw6 = 0.7 * 0.1 + 0 * 0.3 = 0.07
И конечно не забываем про I1 и I2, ведь у них тоже есть синапсы веса которых нам тоже нужно обновить. Однако помним, что нам не нужно находить дельты для входных нейронов так как у них нет входных синапсов.
Теперь давайте убедимся в том, что мы все сделали правильно и снова посчитаем выход НС только уже с обновленными весами.
H2input = 1 * 0.73 + 0 * 0.124 = 0.73
H2output = sigmoid(0.73) = 0.675
Результат — 0.37, ошибка — 39%.
Как мы видим после одной итерации МОР, нам удалось уменьшить ошибку на 0.04 (6%). Теперь нужно повторять это снова и снова, пока ваша ошибка не станет достаточно мала.
Что еще нужно знать о процессе обучения?
Нейросеть можно обучать с учителем и без (supervised, unsupervised learning).
Обучение с учителем — это тип тренировок присущий таким проблемам как регрессия и классификация (им мы и воспользовались в примере приведенном выше). Иными словами здесь вы выступаете в роли учителя а НС в роли ученика. Вы предоставляете входные данные и желаемый результат, то есть ученик посмотрев на входные данные поймет, что нужно стремиться к тому результату который вы ему предоставили.
Обучение без учителя — этот тип обучения встречается не так часто. Здесь нет учителя, поэтому сеть не получает желаемый результат или же их количество очень мало. В основном такой вид тренировок присущ НС у которых задача состоит в группировке данных по определенным параметрам. Допустим вы подаете на вход 10000 статей на хабре и после анализа всех этих статей НС сможет распределить их по категориям основываясь, например, на часто встречающихся словах. Статьи в которых упоминаются языки программирования, к программированию, а где такие слова как Photoshop, к дизайну.
Существует еще такой интересный метод, как обучение с подкреплением (reinforcement learning). Этот метод заслуживает отдельной статьи, но я попытаюсь вкратце описать его суть. Такой способ применим тогда, когда мы можем основываясь на результатах полученных от НС, дать ей оценку. Например мы хотим научить НС играть в PAC-MAN, тогда каждый раз когда НС будет набирать много очков мы будем ее поощрять. Иными словами мы предоставляем НС право найти любой способ достижения цели, до тех пор пока он будет давать хороший результат. Таким способом, сеть начнет понимать чего от нее хотят добиться и пытается найти наилучший способ достижения этой цели без постоянного предоставления данных “учителем”.
Также обучение можно производить тремя методами: стохастический метод (stochastic), пакетный метод (batch) и мини-пакетный метод (mini-batch). Существует очень много статей и исследований на тему того, какой из методов лучше и никто не может прийти к общему ответу. Я же сторонник стохастического метода, однако я не отрицаю тот факт, что каждый метод имеет свои плюсы и минусы.
Вкратце о каждом методе:
Стохастический (его еще иногда называют онлайн) метод работает по следующему принципу — нашел Δw, сразу обнови соответствующий вес.
Пакетный метод же работает по другому. Мы суммируем Δw всех весов на текущей итерации и только потом обновляем все веса используя эту сумму. Один из самых важных плюсов такого подхода — это значительная экономия времени на вычисление, точность же в таком случае может сильно пострадать.
Мини-пакетный метод является золотой серединой и пытается совместить в себе плюсы обоих методов. Здесь принцип таков: мы в свободном порядке распределяем веса по группам и меняем их веса на сумму Δw всех весов в той или иной группе.
Что такое гиперпараметры?
Гиперпараметры — это значения, которые нужно подбирать вручную и зачастую методом проб и ошибок. Среди таких значений можно выделить:
Что такое сходимость?
Сходимость говорит о том, правильная ли архитектура НС и правильно ли были подобраны гиперпараметры в соответствии с поставленной задачей. Допустим наша программа выводит ошибку НС на каждой итерации в лог. Если с каждой итерацией ошибка будет уменьшаться, то мы на верном пути и наша НС сходится. Если же ошибка будет прыгать вверх — вниз или застынет на определенном уровне, то НС не сходится. В 99% случаев это решается изменением гиперпараметров. Оставшийся 1% будет означать, что у вас ошибка в архитектуре НС. Также бывает, что на сходимость влияет переобучение НС.
Что такое переобучение?
Переобучение, как следует из названия, это состояние нейросети, когда она перенасыщена данными. Это проблема возникает, если слишком долго обучать сеть на одних и тех же данных. Иными словами, сеть начнет не учиться на данных, а запоминать и “зубрить” их. Соответственно, когда вы уже будете подавать на вход этой НС новые данные, то в полученных данных может появиться шум, который будет влиять на точность результата. Например, если мы будем показывать НС разные фотографии яблок (только красные) и говорить что это яблоко. Тогда, когда НС увидит желтое или зеленое яблоко, оно не сможет определить, что это яблоко, так как она запомнила, что все яблоки должны быть красными. И наоборот, когда НС увидит что-то красное и по форме совпадающее с яблоком, например персик, она скажет, что это яблоко. Это и есть шум. На графике шум будет выглядеть следующим образом.
Видно, что график функции сильно колеблется от точки к точке, которые являются выходными данными (результатом) нашей НС. В идеале, этот график должен быть менее волнистый и прямой. Чтобы избежать переобучения, не стоит долго тренировать НС на одних и тех же или очень похожих данных. Также, переобучение может быть вызвано большим количеством параметров, которые вы подаете на вход НС или слишком сложной архитектурой. Таким образом, когда вы замечаете ошибки (шум) в выходных данных после этапа обучения, то вам стоит использовать один из методов регуляризации, но в большинстве случаев это не понадобиться.