что больше сумма катетов или гипотенуза

Теорема Пифагора

Основные понятия

Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Гипотенуза — сторона, лежащая напротив прямого угла.

Катет — одна из двух сторон, образующих прямой угол.

Формула Теоремы Пифагора выглядит так:

где a, b — катеты, с — гипотенуза.

Из этой формулы можно вывести следующее:

Для фигуры со сторонами a, b и c, где c самая длинная сторона действуют следующие правила:

Теорема Пифагора: доказательство

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано: ∆ABC, в котором ∠C = 90º.

Пошаговое доказательство:

a 2 + b 2 = c * HB + c * AH

a 2 + b 2 = c * (HB + AH)

Обратная теорема Пифагора: доказательство

Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такая фигура является прямоугольной.

Дано: ∆ABC

Доказать: ∠C = 90º

Пошаговое доказательство:

Обратная теорема доказана.

Решение задач

Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 10 см. Какое значение у гипотенузы?

значит c 2 = a 2 + b 2 = 6 2 + 10 2 = 36 + 100 = 136

Задание 2. Является ли фигура со сторонами 8 см, 9 см и 11 см прямоугольным треугольником?

Ответ: треугольник не является прямоугольным.

Источник

Теорема Пифагора

Теорема Пифагора является одной из важнейших теорем в геометрии.

Формулировка у теоремы такая:
в прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов.

Зная формулировку теоремы Пифагора и две стороны прямоугольного треугольника:
два катета либо катет и гипотенузу, можно найти третью сторону треугольника,
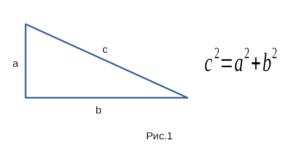
соответственно: гипотенузу либо катет. На рисунке 1 изображен
прямоугольный треугольник и формулировка теорема Пифагора.

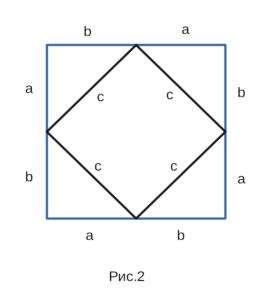
Доказательство теоремы Пифагора

Для доказательства этой теоремы, нарисуем прямоугольный треугольник.
Ради удобства обозначим гипотенузу латинской буквой с, а катеты латинскими
буквами a и b. Докажем, что в прямоугольном треугольнике квадрат гипотенузы
равен сумме квадратов катетов, или иначе \( c^2=a^2+b^2 \).

Теорема доказана.

Следствия из теоремы Пифагора

У этой теоремы много следствий, которые используются при доказательстве
других теорем и некоторых свойств. Перечислим основные из них:

Источник

Прямоугольный треугольник. Теорема Пифагора.

теория по математике 📈 планиметрия

Если в треугольнике есть угол, равный 90 градусов, то такой треугольник называется прямоугольным. Стороны прямоугольного треугольника называются – катеты и гипотенуза. Катеты – это стороны, образующие прямой угол. Гипотенуза – сторона, которая располагается напротив прямого угла.

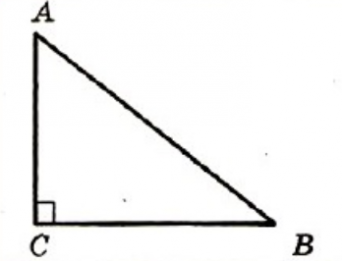
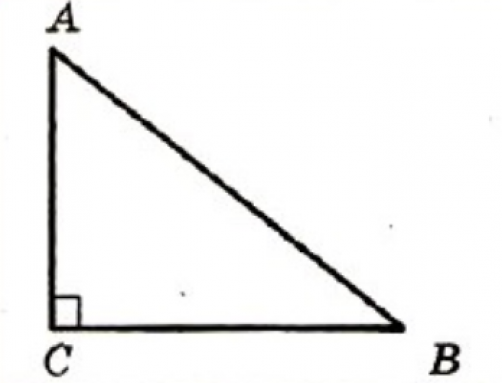
На рисунке треугольник АВС – прямоугольный, угол С равен 90º, стороны АС и ВС – катеты, а сторона АВ – гипотенуза.

Свойства прямоугольного треугольника

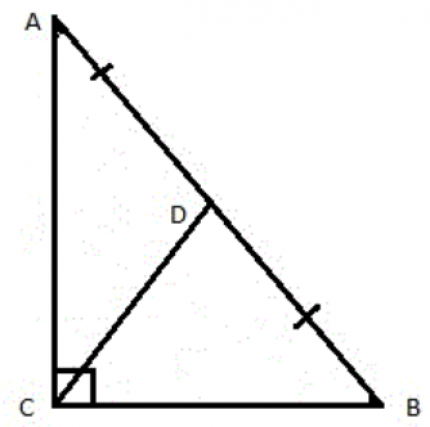
На рисунке изображен прямоугольный треугольник АВС, где CD – медиана, проведенная к гипотенузе. По свойству – медиана CD=0,5АВ, то есть AD=DB=CD.

Признаки равенства прямоугольных треугольников

Существует 4 признака равенства прямоугольных треугольников:

Чтобы быстрее запомнить данные признаки, можно использовать их краткую трактовку:

Теорема Пифагора

Древнегреческий философ, ученый, математик – Пифагор Самосский вывел теорему, которая до сих применима для решения задач. Теорема названа в честь него – «теорема Пифагора».

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

На рисунке в прямоугольном треугольнике АВ 2 =АС 2 +ВС 2

Египетский треугольник

Треугольник со сторонами 3, 4 и 5 см называют Египетским треугольником.

Пифагоровы тройки

Источник

Прямоугольный треугольник

Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Признаки равенства прямоугольных треугольников

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

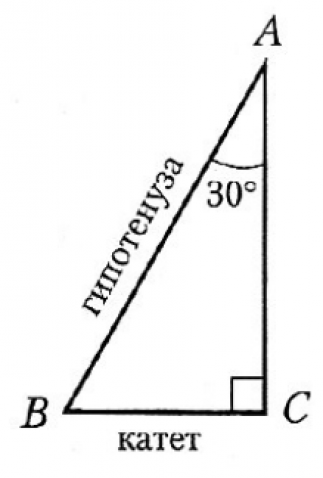
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

, где – катеты, – гипотенуза. Видеодоказательство

4. Площадь прямоугольного треугольника с катетами :

5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

Источник

Что больше сумма катетов или гипотенуза

Основные метрические сооьтношения в прямоугольном треугольнике

§1. Прямоугольный треугольник. Метрические соотношения.

Основные метрические сооьтношения в прямоугольном треугольнике

Пусть `ABC` прямоугольный треугольник с прямым углом `C` и острым углом при вершине `A`, равным `alpha` (рис. 1).

Используем обычные обозначения:

`a_c` и `b_c` – проекции `BD` и `AD` катетов на гипотенузу;

`h` – высота `CD`, опущенная на гипотенузу;

`m_c` – медиана `CM`, проведённая к гипотенузе;

`R` – радиус описанной окружности;

`r` – радиус вписанной окружности.

`sin alpha = a/c`, `cos alpha = b/c` и `»tg»alpha = a/b`.

Значения синуса, косинуса и тангенса острого угла прямоугольного треугольника зависят только от меры угла и не зависят от размеров и расположения треугольника.

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:

`c^2 = a^2 + b^2`

Доказательство теоремы повторите по учебнику.

Выведем ряд соотношений между элементами прямоугольного треугольника.

Квадрат катета равен произведению гипотенузы и его проекции на гипотенузу

Квадрат высоты, опущенной на гипотенузу, равен произведению проекции катетов на гипотенузу

Из треугольника `ACD` (рис. 1) имеем `»tg»alpha = (CD)/(AD)`, а из треугольника `BCD` `»tg»alpha = (BD)/(CD)`.

Значит `(BD)/(CD) = (CD)/(AD)`, откуда `CD^2 = AD * BD`, т. е. `h^2 = a_c * b_c`.

Произведение катетов равно произведению гипотенузы и высоты, опущенной на гипотенузу

Из треугольника `ABC` имеем `sin alpha = (BC)/(AB)`, а из треуольника `ACD` `sin alpha = (CD)/(AC)`.

Таким образом, `(BC)/(AB) = (CD)/(AC)`, откуда `BC * AC = AB * CD`, т. е. `a * b = c * h`.

Медиана, проведённая к гипотенузе, равна половине гипотенузы, т. е.

.

Полезно также запомнить, что медиана к гипотенузе разбивает треугольник на два равнобедренных треугольника.

Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы

Это следует из Свойства 4, действительно, `MA = MB = MC`, следовательно, окружность с центром в точке `M` и радиуса `c/2` проходит через три вершины.

Сумма катетов равна удвоенной сумме радиусов описанной и вписанной окружностей

`a + b = 2(R + r)` или `a + b = c + 2r`

Равенства, доказанные в Свойствах 1 и 2, записываются также как:

Источник