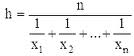что больше среднее арифметическое или среднее геометрическое
Что больше среднее арифметическое или среднее геометрическое
Зачастую в средних класах мы пользуемся известным выражением о том, что среднее арифметическое двух неотрицательных чисел больше чем среднее геометрические их значение:
Доказывается неравенство достаточно просто. Умнажаем обе части на 2 и переносим правую честь влево:
Что и требовалось доказать.
Для двух положительных чисел оно имеет следующий вид (общий случай для n чисел):
Пусть a, b ∈ R, тогда иммет место неравенство:
Докажем его. Покажем, что среднее геометрическое больше, чем среднее гармоническое.
Что и требовалось доказать.
Соотношение между средним арифметическим и средним геометрическим рассматривалось выше. Докажем, что среднее квадратическое больше среднего арифметического:
√ (a 2 + b 2 ) / 2 ≥ (a + b) / 2; так как справа положительное число, подносим в квадрат обе части:
(a 2 + b 2 ) / 2 ≥ (a 2 + 2ab + b 2 ) / 4; переносим все в левую часть, умножаем на 4:
Что и требовалось доказать.
Неравенство имеет место для n чисел и звучит так:
На данный момент в базе присутствует информация о 1847 великих математиках.
Для ознакомления доступны 48 книг.
Добавлен материал «Показательные уравнения и неравенства», в котором заполнены разделы «Теория» и «Методы решений». В ближайшее время ожидайте задачи по этому материалу.
Неравенство о среднем арифметическом и среднем геометрическом
Неравенство о среднем арифметическом и среднем геометрическом (неравенство Коши)
Среднее арифметическое n положительных чисел не меньше их среднего геометрического:
причём равенство достигается тогда и только тогда, когда
Частный случай этого неравенства, связывающий среднее арифметическое и среднее геометрическое двух положительных чисел, известен с древних времён. Чаще всего его доказывают, используя геометрическую интерпретацию.

Построим окружность с диаметром AB=a+b.
Из произвольной точки C окружности проведём к диаметру перпендикуляр CD.
По свойству прямоугольного треугольника, высота, проведённая к гипотенузе, равна среднему геометрическому между проекциями катетов на гипотенузу:
Соединим точку C с центром окружности, точкой O. CO — радиус, значит, он равен половине диаметра:
то есть длина CO равна среднему арифметическому a и b.
В прямоугольном треугольнике COD CD — катет, CO — гипотенуза.
Так как гипотенуза всегда больше катета, CO>CD, следовательно, среднее арифметическое a и b больше их среднего геометрического.

если AO=BO, то есть a=b.
(так как a>0), и и ф этом случае среднее арифметическое a и b равно их среднему геометрическому.
Таким образом, среднее арифметическое положительных чисел a и b не меньше их среднего геометрического.
В общем случае неравенство было доказано Коши.
Правильное среднее
Существует много видов средних, но в каждой ситуации только одно из них правильное. Только один вид среднего следует использовать в каждом конкретном случае, и ошибка может вам стоить очень дорого.
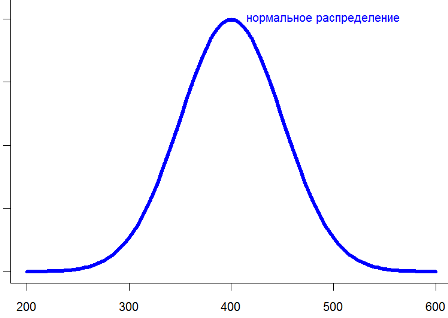
Дело в том, что в основе такого усреднения лежит закон больших чисел и допущение, что исходная величина распределена нормально. А это подразумевает, что возможные значения сконцентрированы вокруг некоторого наиболее частого значения, а отклонения и в большую, и в меньшую сторону относительно невелики и равновероятны.
В следующих записях я приведу интересные примеры неправильного усреднения, а сейчас перейдем к другим видам среднего.
Сначала, наверное, может показаться, что правильное значение 65 км/ч, потому что (50+80)/2 = 65.
Однако быстро становится понятно, что если бы другой автомобиль двигался со средней скоростью, то он провел бы в пути столько же времени, что и первый. Именно в этом смысл усреднения в данном случае.
И вот тут на помощь приходит среднее гармоническое:
Для нашей задачи искомое среднее равно 2/(1/50+1/80)=61.54 км/ч. И действительно в первом случае автомобиль затратил 2 часа на преодоление 100 км со скоростью 50 км/ч и еще 1.25 часа ему потребовалось на следующие 100 км, потому что скорость возросла до 80 км/ч. Таким образом, всего ушло 3.25 часа.
Если бы автомобиль все 200 км двигался со скоростью 61.54 км/ч, то у него также ушло бы на дорогу 3.25 часа.
Можно предположить, что есть несколько вариантов усреднения. Во-первых, среднее арифметическое: (12+42)/2 = 27%. Во-вторых, сложный процент: 1.12*1.42=1.5904, т.е. 59.04% за 2 года или 28.02% за год.
Но «в среднем» означает, что применив это значение к каждому году, мы получим тот же самый результат, что и при использовании множества исходных значений.
Проверяем. Среднее арифметическое: 1.27*1.27=1.6129 (на 61.29%). Сложный процент: 1.2802*1.2802=1.6389 (на 63.89%). Результаты мало того, что разные, так и оба неправильные, потому что выручка за 2 года выросла на 59.04%.
Среднее геометрическое часто встречается в реальных бизнес-задачах вместе с процентами и долями. Если в вашей задаче что-то растет или падает и вы хотите усреднить динамику показателя, то вам следует применять среднее геометрическое.
Вместо заключения
Повторю главные моменты:
— среднее арифметическое далеко не всегда соответствует смыслу и физической сущности усредняемого показателя;
— существует много видов средних значений, но в каждом конкретном случае есть только один правильный вид среднего, и именно его следует использовать в расчетах.
В среднем вы используете неправильное среднее: геометрические и гармонические средства в анализе данных
Дата публикации Jan 28, 2018
ПРЕДИСЛОВИЕ
(пропустите это, если у вас уже есть «центральная тенденция»)
Это, вероятно, самая распространенная задача анализа данных:
У вас есть куча цифр. Вы хотите суммировать их с меньшим числом цифр, предпочтительно одним числом. Таким образом, вы складываете все числа, а затем делите сумму на общее количество чисел. Бум: вот «средний«, правильно?
Вопреки общему мнению,среднийматематически говоря, это не вещь. Смысл:нет математической операции, которая называется «средняя», Что мыобычно подразумевают подсредний«среднее арифметическое», известная операция, описанная выше. Мы называем это «средним», потому что ожидаем, что оно будет соответствовать разговорному определению «среднего»: типичное «нормальное» или среднее значение. Часто мы правы, но реже, чем мы думаем.
Сводные статистические данные
Среднее арифметическое является лишь одним из многих способов получения «среднего» значения. С технической точки зрения, они известны каксводные статистические данные»,«меры центральной тенденции» или «меры местоположения».
Наверное, 2-й самый известныйсводная статистикаэтомедиана— буквальное среднее значение набора данных (которое, как таковое, часто является более «средним», чем среднее). Я не буду обсуждать это здесь, но достаточно сказать, чтосреднее арифметическоечрезмерно используется во многих случаях, когдамедианаболее уместно. дальнейшее чтениеВот,Вот&Вот(последний частично совпадает с остальной частью этой статьи, и это очень хорошо).
Эта статья будет посвящена двум менее известным мерам: геометрический&гармоника средства,
Часть Iразвивает концептуальное, интуитивное и практическое понимание того, как они работают и когда их использовать.
Часть IIЭто отдельная статья, которая становится немного более глубокой и технической, демонстрируя их динамику с помощью кода R, реальных и смоделированных данных и графиков.
I. Пифагорейские средства
среднее арифметическоеэто просто 1 из 3 ‘Пифагорейские средства’(Назван в честь Пифагора и его родственников, которые изучали их пропорции). Как и было предсказано,геометрический&гармоникасредствазакруглить трио.
Чтобы понять основы их функционирования, давайте поработаем над знакомым средним арифметическим.
Среднее арифметическое
арифметиказначит, правильно назван: мы находим его подобавлениевсе числа в наборе данных, затем деление на сколько чисел в наборе данных (чтобы привести сумму обратно к масштабу исходных чисел).
3 + 8 + 10 = 21
21 ÷ 3 = 7
Arithmetic mean = 7
Обратите внимание, что мы, по сути, говорим здесь:если каждый номер в нашем наборе данныхбыл тот же номеркакое число это должно бытьчтобы иметь то же самое sum как наш фактический набор данных?
Но в добавлении нет ничего особенного. Это всего лишь одна довольно простая математическая операция. Среднее арифметическое хорошо работает для получения «среднего» числа набора данных, когда естьприсадкасвязь между числами. Такие отношения часто называют «линейный”, Потому что при построении графика в порядке возрастания или убывания числа имеют тенденцию падать на или вокруг прямой линии. Простым идеализированным примером будет набор данных, в котором каждое число создается путем добавления 3 к предыдущему числу:
среднее арифметическоетаким образом дает нам вполне разумное среднее значение:
(1 + 4 + 7 + 10 + 13 + 16 + 19) ÷ 7 = 10
Но не все наборы данных лучше всего описываются этими отношениями. У некоторых естьмультипликативныйилиэкспоненциальныйотношения, например, если мыумноженныйкаждый последовательный номер на 3, а недобавлениена 3, как мы делали выше:
Это производит то, что известно какгеометрическая серия(Подсказка Подсказка). При построении по порядку эти числа больше напоминают кривую, чем прямую линию.
В этой ситуациисреднее арифметическоене подходит для получения «среднего» числа для обобщения этих данных.
(1 + 3 + 9 + 27 + 81 + 243 + 729) ÷ 7 = 156.1
156не особенно близко к большинству чисел в нашем наборе данных. На самом деле это больше, чем5xмедиана(среднее число), которое27,
Этот перекос более очевиден, когда данные нанесены на плоскую числовую линию:
Среднее геометрическое
Square root of 25 = 5, because 5 * 5 = 25
Обратите внимание, что мы говорим здесь:если каждый номер в нашем наборе данныхбыл тот же номеркакое число это должно бытьчтобы иметь тот же мультипликативный product как наш фактический набор данных?
Итак, среднее геометрическое нашего набора данных:
1 * 3 * 9 * 27 * 81 * 243 * 729 = 10,460,353,203
7th root of 10,460,353,203 = 27
geometric mean = 27
И на номерной строке:
В этом случае наше среднее геометрическоеочень сильнонапоминает среднее значение нашего набора данных. На самом деле, это эквивалентномедиана,
Заметка: среднее геометрическое не будетвсегдаравны медиане, только в тех случаях, когда существует точное постоянное мультипликативное соотношение между всеми числами (например, умножение каждого предыдущего числа на 3, как мы это делали). Наборы данных реального мира редко содержат такие точные отношения, но для тех, которые приближают этот тип мультипликативных отношений,среднее геометрическоедаст «среднее число» ближе, чемсреднее арифметическое,
Применение геометрического среднего в реальном мире
Оказывается, что есть много практических применений длясреднее геометрическое, какмультипликативный-ишотношения изобилуют в реальном мире.
Сложный процент
Мы хотели бы воспользоваться сокращением, чтобы определить среднегодовую процентную ставку и, следовательно, нашу общую сумму денег через 5 лет, поэтому мы пытаемся «усреднить» эти ставки:
Затем мы вставляем этот средний% вформула сложного процента:
Просто чтобы убедиться, что мы не обманываем себя, давайте сделаем это далеко и сравним результаты:
Что произошло? Наш ярлык переоценил наши реальные доходы почти на$ 1000,
Мы сделали общую ошибку:Мы применили аддитивную операцию к мультипликативному процессу и получили неточный результат.
Теперь давайте попробуем еще раз ссреднее геометрическое:
1.01 * 1.09 * 1.06 * 1.02 * 1.15 = 1.368837042
5th root of 1.368837042 = 1.064805657
Geometric mean = 1.064805657
Подключитьсреднее геометрическоепроцентных ставок в нашей формуле сложных процентов:
Это больше походит на это.
Мы использовали правильное среднее значение для правильной работы и получили правильный результат.
Для чего еще подходит среднее геометрическое?
Разные весы или единицы
Необычная особенностьсреднее геометрическоеявляется то, что вы можете усреднить по числам насовершенно разные весы,
Например, мы хотим сравнить онлайн-рейтинги для двух кафе, используя два разных источника. Проблема в том, что source 1 использует 5-star масштаб & source 2 использует 100-point масштаб:
Если мы наивно примем среднее арифметическое необработанных оценок для каждого кафе:
Кофешоп А = (4.5 + 68) ÷ 2 = 36.25
Кофейня B = (3 + 75) ÷ 2 = 39
Мы пришли бы к выводу, чтоКофешоп Ббыл победителем.
Если бы мы были немного более подкованы, мы бы знали, что должнынормализуютнаши значения в том же масштабе, прежде чем усреднить их с помощью среднего арифметического, чтобы получить точный результат. Таким образом, мы умножаем source 1 рейтинги 20 вывести их из 5-star масштаб до 100-point масштаб source 2 :
Кофейня A
4.5 * 20 = 90
(90 + 68) ÷ 2 = 79
Кофешоп Б
3 * 20 = 60
(60 + 75) ÷ 2 = 67.5
Итак, мы находим, чтоКофейня Aявляется истинным победителем, вопреки наивному применению среднего арифметического выше.
Однако геометрическое среднее позволяет нам прийти к такому же выводу, не суетясь над шкалой или единицами измерения:
Кофейня Aзнак равно square root of (4.5 * 68) = 17.5
Кофешоп Бзнак равно square root of (3 * 75) = 15
среднее арифметическоепреобладают цифры в большем масштабе, что заставляет нас думатьКофешоп Бэто более высокий рейтинг магазина. Это потому, что среднее арифметическое ожидает аддитивные отношения между числами и не учитывает масштабов и пропорций Отсюда необходимость привести числа в одну шкалу перед применением среднего арифметического.
среднее геометрическоес другой стороны, может с легкостью обрабатывать различные пропорции из-за его мультипликативного характера. Это чрезвычайно полезное свойство, нообратите внимание, что мы теряем: У нас больше нет интерпретируемыхмасштабвообще. Среднее геометрическое эффективнобезразмерныйв таких ситуациях.
ОБНОВЛЕНИЕ 14/14/18: КакуказалпоМладен Фернежир, нет никаких гарантий, чтосреднее геометрическоевсегда сохранит порядоксреднее арифметическоена масштабированных или нормализованных значениях, гораздо меньше быть пропорциональным, как я изначально указывал. Скорее, это просто другой способ суммировать отношения между различными наборами чисел (хотя тот, который часто будет давать более «достоверные» сводки значений в разных масштабах). Итак, еще раз, осторожность и критическая мысль необходимы для его применения.
Среднее геометрическое резюме
кТЛ; др:
Как и с большинством вещей в жизни, существует несколько железных правил применения геометрического среднего (за пределами сложного интереса и подобных вещей). Существуют некоторые эвристические и практические правила, но в конечном итоге, как всегда, необходимы суждения и научный скептицизмздравый эмпиризм,
Подробнее об этом в заключении ниже, а пока давайте представим наш финальныйСреднее пифагорейское.
Гармоническое среднее
3-е и последнее пифагорейское среднее.
Этот раздел будет короче предыдущего, так как среднее гармоническое еще более эзотерическое, чем среднее геометрическое, но все же стоит понять.
В то время каксреднее арифметическоетребует дополнения исреднее геометрическоеиспользует умножение,среднее гармоническоеутилизируетобратные,
Итак,среднее гармоническоеможно описать словами как: обоюдныйизсреднее арифметическоеизобратныенабора данных,
Там много взаимных сальто, но на самом деле это всего лишь несколько простых шагов:
1. Take the reciprocal of all numbers in the dataset
2. Find the arithmetic mean of those reciprocals
3. Take the reciprocal of that number
В математической записи это выглядит так:
Обратите внимание, что мы говорим здесь:еслиобоюдныйкаждого числа в нашем наборе данныхбыл тот же номеркакое число это должно бытьдля того, чтобы иметь такой же ответный sum как наш фактический набор данных?
(Заметка:благодаря тому факту, что 0 не имеет reciprocal (ничто не может быть умножено на 0 в = 1 ),среднее гармоническоетакже не может обрабатывать наборы данных, содержащие 0 Схожи ссреднее геометрическое.)
Вот так работает сантехника НоДля чего это?
Применение гармонического среднего в реальном мире
Чтобы ответить на это, мы должны ответить:для чего нужны взаимности?
посколькуобратныеКак и все деление, это просто скрытое умножение (а это просто скрытое сложение), мы понимаем:взаимные ссылки помогают нам легче делить на доли,
Но эквивалентный метод будет масштабировать числа 5 & 3/7 к общему знаменателю, затем разделите обычным образом:
5/1 ÷ 3/7 = 35/7 ÷ 3/7 = 35 ÷ 3 = 11 2/3 = 11.66667
Таким образом,среднее гармоническоеестественноприспосабливает другой уровень умножения / деленияпо среднему геометрическому,таким образомэто полезно при работе с наборами данных скоростей или соотношений (то есть дробей) за разные длины или периоды,
SIDEBAR🙁 Возможно, вы думаете:«Подожди, я подумаласреднее геометрическоебыл использован для усреднения интересатарифы&коэффициентыв разных масштабах! »И ты был бы прав. Вы тожене будет первым быть в замешательстве этим, Я сам решил написать эту статью, чтобы прояснить свое собственное мышление и понимание. Так что терпите меня, я надеюсь прояснить это на следующем примере и подытожить все эти различия в заключении этой статьи ниже.)
Средняя скорость путешествия
Канонический пример использованиягармонические средствав реальном мире подразумевает путешествие в физическом пространстве с разными скоростями, то есть со скоростью:
Рассмотрим поездку в продуктовый магазин и обратно:
Какова была ваша средняя скорость на протяжении всей поездки?
Но подумайте еще раз: потому что вы путешествовали быстрее в одном направлении, вы покрыли эти 5 miles быстрее и тратит меньше времени в общем путешествии на этой скорости, поэтому средняя скорость поездки за всю продолжительность поездки не является средней точкой между 30 mph & 10 mph должно быть ближе к 10 mph потому что ты провел больше времени на этой скорости.
Для того, чтобы применитьсреднее арифметическоездесь правильно, мы должны были бы определить количество времени, потраченного на поездку по каждой ставке, а затем взвесить наш расчет среднего арифметического значения соответствующим образом:
Поездка Там: (в 30 милях в час)
30 miles per 60 mins = 1 mile every 2 minutes = 1/2 mile every minute
5 miles at 1/2 mile per minute = 5 ÷ 1/2 = 10 minutes
«Trip There» time = 10 minutes
Поездка назад: (в 10 милях в час)
10 miles per 60 mins = 1 mile every 6 minutes = 1/6 miles every minute
5 miles at 1/6 mile per minute = 5 ÷ 1/6 = 30 minutes
«Trip Back» time = 30 minutes
Total trip time = 10 + 30 = 40 minutes
Давайте попробуем это снова, используясреднее гармоническое,
Et voilà! ²
Наша истинная средняя скорость поездки,автомагическис учетом времени, потраченного на поездку в каждом направлении =15 миль в час!
Обратите внимание на несколько вещей:
Как и в случае сложных процентов исреднее геометрическоеЭто пример точного, объективно правильного применениясреднее гармоническое, Но опять же, не всегда все так ясно. Есть и другие точные, математически обоснованныеПриложенияв области физики, финансов, гидрологии и даже (по договоренности) вбейсбольная статистика, Больше уместно для науки о данных: это часто применяется кточность и отзывв оценке моделей машинного обучения.
Но чаще всего это суждение, зависящее от ловкого понимания ваших данных и поставленной задачи.
Я постараюсь прояснить и обобщить тонкости ниже.
ЧАСТЬ I ЗАКЛЮЧЕНИЕ
Подведем итоги того, что мы уже продемонстрировали:
1. Три пифагорейских средства тесно связаны и могут быть выражены как частный случай друг друга.
Например, мы увидели, что:
ВЧасть II(отдельный пост, чтобы следовать), мы увидим, что должно быть понятно тем, кто уже знаком с мультипликативными преобразованиями:среднее геометрическоенабора данных эквивалентносреднее арифметическоеизлогарифмыкаждого числа в этом наборе данных. Так же, каксреднее гармоническоеэто простосреднее арифметическоес несколькими взаимными преобразованиями,среднее геометрическоеэто простосреднее арифметическоеспреобразование журнала,
Если каждый означать это всего лишь трансформация или переформулировка другого, как эти трансформации взаимодействуют и влияют на ваши результаты?
2. Пифагорейские средства соответствуют строгим порядковым отношениям.
Из-за их соответствующих уравнений: среднее гармоническоевсегда меньше, чемсреднее геометрическое, который всегда меньше, чемсреднее арифметическое,
Три средства находятся ближе или дальше друг от друга в зависимости от распространения лежащих в основе данных.единственное исключение из этого правилапроисходит в крайнем случае, когда все числа в наборе данных являются одинаковыми точными числами, и в этом случае все 3 средних также эквивалентны. Таким образом,последующийнеравенстводержит:
harmonic mean ≤ geometric mean ≤ arithmetic mean
Эти пропорции можно наблюдать в геометрическом изображениипифагореец(+ квадратичный)Средствав начале этого раздела.
Признание этих отношений очень помогает в понимании того, когда применять каждое среднее значение и как будет влиять на ваши результаты.
Чтобы сделать это более конкретным, давайте вернемся к нашим исходным наборам аддитивных и мультипликативных данных со всеми тремя средствами, изображенными в каждом:
Набор аддитивных данных <1, 4, 7, 10, 13, 16, 19… >
Harmonic mean = 4.3
Geometric mean = 7.3
Arithmetic mean = 10
Очевидно, чтогеометрический&гармоникасредствапохоже, существенно занижает «середину» этого линейного аддитивного набора данных. Это потому, что эти средства более чувствительны к меньшим числам, чем к большим числам (делая их также относительнонечувствительныйк большим выбросам).
Мультипликативный набор данных <1, 3, 9, 27, 81, 243, 729… >
Harmonic mean = 4.7
Geometric mean = 27
Arithmetic mean = 156.1
Здесьсреднее геометрическоенаходится точно в порядковой середине набора данных, в то время каксреднее гармоническоепо-прежнему пересекает низкую сторону исреднее арифметическоесильно отклоняется к высокой стороне, вытягивается большими выбросами.
3 Есть некоторые жесткие правила, немного эвристики и много места для суждений
Если есть один TL; DR для всей этой части, это будет:
Пожалуйста, прокомментируйте ниже свои собственные случаи использования и опыт работы с меньшимиПифагорейские средства(а также любые опечатки, которые вы можете обнаружить в этой части!).
Проверять, выписыватьсяЧасть IIэтого поста, который обходится без концептуальных рассказов в пользу более краткой, экономичной и технической обработки предмета с реальными и смоделированными данными, распределениями, графиками и сопровождающим R-кодом.
ИСПРАВЛЕНИЕ 7/14/18:Предыдущая версия этой статьи гласила:среднее геометрическоеизбаллы по разным шкалампропорциональносреднее арифметическоекогда эти значения нормированы на общую шкалу ».Младен Фернежируказалчто это не правда. Спасибо за исправление!