что больше сотые или десятые после запятой
Сравнение десятичных дробей
Одно и то же натуральное число может быть представлено в виде обыкновенной дроби разными способами, например, 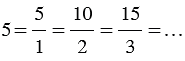
Если к десятичной дроби приписать справа какое угодно количество нулей, то получится дробь равная данной.
Пример:
Пример:
1) 3,40 = 3,4; 2) 0,50600 = 0,506; 3) 5,870000 = 5,87.
| Любое натуральное число можно представить в виде десятичной дроби с каким угодно количеством нулей после запятой. |
Пример:
| Из двух десятичных дробей с разными целыми частями больше та дробь, у которой целая часть больше. |
Пример:
1) 3,5 
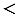
| Из двух десятичных дробей с одинаковыми целыми частями и равным количеством цифр после запятой больше будет та дробь, у которой больше первая (при чтении слева направо) из неодинаковых цифр их дробных частей (поразрядное сравнение). |
Пример:
1) 15,2 
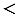

| Чтобы сравнить две десятичные дроби с равными целыми частями и различным количеством цифр после запятой, надо с помощью приписывания нулей справа уравнять количество цифр в дробных частях, после чего сравнить полученные дроби поразрядно (смотри правило выше). |
Пример:
Сравнить десятичные дроби 45,6 и 45,498.
Решение:
У дроби 45,6 одна цифра после запятой, а у дроби 45,498 три цифры после запятой, для того, чтобы сравнить данные дроби, приписываем к дроби 45,6 справа два нуля, получим новую дробь 45,600. Теперь поразрядно сравниваем дроби 45,600 и 45,498, получим 45,600 


Поделись с друзьями в социальных сетях:
Сравнение десятичных дробей
Понятие десятичной дроби
Прежде чем мы расскажем, как сравнивать десятичные дроби, вспомним основные определения, виды дробей и разницу между ними.
Дробь — это число в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Ее записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это когда количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Основные свойства
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Правило сравнения десятичных дробей
Чтобы сравнить две десятичные дроби, сначала нужно сравнить их целые части. Если целые части равны, продолжаем искать первый несовпадающий разряд. Большей будет та дробь, у которой соответствующий разряд больше.
Вот так с первой строчки раскрыли тему сравнения десятичных дробей 😜 Но это еще не все — едем дальше.
Алгоритм сравнения десятичных дробей
Применим правило на практике. Сравним десятичные дроби: 15,7 и 15,719.
Целую часть с целой частью: 15 = 15. Целые части равны.
Десятые с десятыми: 7 = 7. Десятые также равны.
Чтобы сравнить две десятичные дроби, нужно уравнять количество знаков после запятой (приписать к одной из них справа нули), затем отбросить запятую, и сравнить два натуральных числа.
Сравним 3,656 и 3,48.
Урок 41 Бесплатно Сравнение десятичных дробей
Сравнение чисел- это математическая операция, с помощью которой можно установить равенство или неравенство чисел, если числа не равны, то с помощью данной операции можно выяснить какое число больше, а какое меньше.
Сравнивать можно любые числа в том числе и десятичные дроби.
Десятичные дроби будем сравнивать с помощью их десятичной записи.
Сегодня на уроке научимся определять разрядность десятичной дроби, разберем правила сравнения десятичных дробей.
Определим, где на координатном луче расположена десятичная дробь.
Разряды десятичных дробей
В десятичных дробях, так же, как и в натуральных числах, значение каждой цифры зависит от ее места (позиции) в числе.
Каждый знак в записи десятичной дроби означает сколько единиц соответствующего разряда содержится в ней, а единица каждого разряда содержит 10 единиц предыдущего разряда.
В десятичной дроби до запятой (в целой части десятичной дроби) название разрядов точно такое же, как в натуральных числах: единицы, десятки, сотни, тысячи и т.д.
Каждая цифра десятичной дроби, стоящая после десятичной запятой (в дробной части) тоже имеют свое название и значение.
Номер разряда в целой части отсчитывается влево от запятой, а в дробной части- вправо от запятой.
Разряды в десятичных дробях отличаются по старшинству: старшинство убывает слева на право.
Самым старшим (высшим) разрядом считается самая левая цифра в числе, самым младшим разрядом (низшим) разрядом является самая правая цифра в числе.
Цифры, стоящие после десятичной запятой, называют десятичными знаками.
Итак, если после десятичной запятой стоит один знак- это десятые, если после запятой два знака- это сотые, если три десятичных знака- это тысячные и т.д.
Таким образом, первая цифра после запятой обозначает разряд десятых (\(\mathbf<\frac<1> <10>= 0,1>\)), далее идет разряд сотых (\(\mathbf<\frac<1> <100>= 0,01>\)), затем разряд тысячных (\(\mathbf<\frac<1> <1000>= 0,001>\)) и т.д.
Давайте составим таблицу разрядов десятичных дробей.
На основе вышеизложенной информации рассмотрим поясняющий пример.
Составим таблицу разрядов для числа 175,248.
Из таблицы видно, что заданное число 175,248 содержит 1 сотню, 7 десятков, 5 единиц, 2 десятых, 4 сотых, 8 тысячных.
Данная десятичная дробь читается так: «сто семьдесят пять целых двести сорок восемь тысячных».
Наверное, вы заметили, что в нашем примере, в таблице, в разряде десятитысячных мы поставили нуль, и в наших действиях нет никакой ошибки.
Справа от запятой после самой последней цифры, неравной нулю, можно приписывать сколько угодно нулей, от этого значение десятичной дроби не изменится.
75,248 = 75,2480 = 75,24800 = …
Верно и обратное действие: если в конце десятичной дроби, после самой правой ненулевой цифры стоят только нули, то эти нули можно отбросить, в результате получится по значению та же самая дробь.
75,24800 = 75,2480 = 75,248
Нули, стоящие в целой части десятичной дроби, перед самой левой ненулевой цифрой, эту десятичную дробь не изменяют.
75,248 = 075,248 = 0075,248 = 00075,248 = …
У меня есть дополнительная информация к этой части урока!
Нули, стоящие между десятичными знаками, убирать и дописывать ни в коем случае нельзя.
Нуль, стоящий между десятичными знаками несет в себе информацию о том, что в данном разряде отсутствуют единицы.
Например, 2,05 ≠ 2,5.
2,05 и 2,5- это абсолютно два разных числа.
2,05— две целых пять сотых.
2,5— две целых пять десятых.
Любую десятичную дробь можно представить в виде суммы, т.е. разложить по разрядам.
Сумма разрядных слагаемых- это запись числа в виде суммы его разрядных единиц.
Делается это так же просто, как и для натуральных чисел.
Попробуем разложить десятичную дробь по разрядам на примере.
Разложите десятичную дробь 43,2086.
Число 43,2086 содержит следующие разряды:
Число содержит 4 десятка, 3 единицы, 2 десятых, 0 сотых, 8 тысячных, 6 десятитысячных.
В результате получаем:
43,2086 = 40 + 3 + 0,2 + 0,00 + 0,008 + 0,0006
Пройти тест и получить оценку можно после входа или регистрации
Изображение десятичной дроби на координатном луче
Десятичную дробь, как и любое другое число, можно отметить на координатном луче.
Десятичные дроби на координатном луче изображают так же, как обыкновенные дроби (смешанные числа), поскольку десятичная дробь и соответствующая ей обыкновенная дробь- это одно и тоже число.
Для того чтобы отметить на координатном луче точку, которая будет соответствовать заданной десятичной дроби, нужно перевести эту десятичную дробь в обыкновенную дробь (смешанное число).
Отметим на координатном луче точку А(0,5) и точку В(1,3).
Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.
По условию нам даны десятичные дроби с одним десятичным разрядом, следовательно, соответствующие им обыкновенные дроби, содержат в знаменателе число 10.
Десятичной дроби 0,5 соответствует обыкновенная правильная дробь \(\mathbf<\frac<5><10>>\).
Десятичной дроби 1,3 соответствует смешанное число \(\mathbf<1\frac<3><10>>\).
Так как знаменатель полученных нами обыкновенных дробей равен десяти, разобьем единичный отрезок на десять равных частей (долей), каждая такая часть будет равна \(\mathbf<\frac<1><10>>\) (одной десятой) единичного отрезка ОЕ.
1. Правильная дробь \(\mathbf<\frac<5><10>>\)- это часть единичного отрезка, представляет собой 5 частей из десяти.
Отметим точку А(\(\mathbf<\frac<5><10>>\)) на координатном луче, для этого отсчитаем от начала координат пять частей (долей) единичного отрезка.
Так как \(\mathbf<\frac<5><10>>\) и 0,5— это одно и тоже число, следовательно, А(\(\mathbf<\frac<5><10>>\)) и А(0,5)- это одна и та же точка на координатном луче.
Обозначим на координатном луче точку В с координатой \(\mathbf<1\frac<3><10>>\).
Чтобы изобразить смешанное число \(\mathbf<1\frac<3><10>>\) отсчитаем от начала координат один целый единичный отрезок, а от второго единичного отрезка возьмем только три доли из десяти.
Отметим точку В(\(\mathbf<1\frac<3><10>>\)) на координатном луче.
Смешанное число и соответствующая ему неправильная дробь принадлежат одной точке координатного луча.
Переведем смешанное число \(\mathbf<1\frac<3><10>>\) в неправильную дробь, получим:
Так, если отсчитать от начала координат 13 частей единичного отрезка, каждый из которых равен \(\mathbf<\frac<1><10>>\) отрезка ОЕ, то в результате окажемся в точке с координатой \(\mathbf<\frac<13><10>>\).
В этой же точке мы ранее отметили точку В(\(\mathbf<1\frac<3><10>>\)).
Следовательно, точка с координатой 1,3, точка с координатой \(\mathbf<1\frac<3><10>>\) и точка с координатой \(\mathbf<\frac<13><10>>\)- это одна и та же точка на координатном луче.
В десятичной дроби справа от запятой после самой последней цифры, неравной нулю, можно приписывать сколько угодно нулей, в результате чего значение десятичной дроби не изменяется.
Например, 0,2 = 0,20
Равные десятичные дроби на координатном луче изображаются одной и той же точкой.
Точка с координатой 0,2 и точка с координатой 0,20— это одна и та же точка на координатном луче.
Меньшая десятичная дробь на координатном луче располагается левее, большая- правее.
Рассмотрим, как относительно друг друга на координатном луче расположены точки С(0,2), D(0,5), K(0,7).
Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.
По условию нам даны десятичные дроби с одним десятичным разрядом, следовательно, соответствующие им обыкновенные дроби, содержат в знаменателе число 10.
Так как знаменатель полученных нами обыкновенных дробей равен десяти, разобьем единичный отрезок на десять равных частей (долей), каждая такая часть будет равна \(\mathbf<\frac<1><10>>\) (одной десятой) единичного отрезка ОЕ.
Десятичной дроби 0,2 соответствует обыкновенная правильная дробь \(\mathbf<\frac<2><10>>\).
Дробь \(\mathbf<\frac<2><10>>\)- это часть единичного отрезка, представляет собой 2 части из десяти (две доли единичного отрезка ОЕ).
Десятичной дроби 0,5 соответствует обыкновенная правильная дробь \(\mathbf<\frac<5><10>>\).
Дробь \(\mathbf<\frac<5><10>>\) представляет собой 5 частей из десяти (пять долей единичного отрезка ОЕ).
Десятичной дроби 0,7 соответствует обыкновенная правильная дробь \(\mathbf<\frac<7><10>>\).
Дробь \(\mathbf<\frac<7><10>>\)- это часть единичного отрезка, представляет собой 7 частей из десяти (семь долей единичного отрезка ОЕ).
Точка С с координатой 0,2 лежит левее точки D(0,5) и точки K(0,7), следовательно, десятичная дробь 0,2 меньше десятичных дробей 0,5 и 0,7.
Точка D с координатой 0,5 лежит правее точки С(0,2) и левее точки K(0,7), следовательно, десятичная дробь 0,5 больше 0,2 и меньше 0,7.
Пройти тест и получить оценку можно после входа или регистрации
Сравнение десятичных дробей
Содержание
Сравнение десятичных дробей похоже на сравнение натуральных чисел. Сравнивать десятичные дроби проще, чем обыкновенные.
Свойство десятичных дробей
Какой можно сделать вывод?
Эти дроби равны друг другу:
Если в конце десятичной дроби приписать нуль или отбросить нуль, получится дробь, равная данной.
Это свойство десятичных дробей очень пригодится нам для того, чтобы сравнивать дроби.
Как сравнивать десятичные дроби: первый способ
Если мы сравниваем дроби с разным количеством знаком после запятой, нужно сделать количество десятичных знаков одинаковым.
Если теперь записать размеры хомячков в виде неправильных дробей, получится так:
У нас две дроби с одинаковыми знаменателями. Значит, больше будет та, у которой больше числитель.
Равенства или неравенства с дробями читаются так же, как и с натуральными числами, при этом склоняются все их части:
четыре целых шестьсот сорок три тысячных больше четырёх целых шестисот сорока одной тысячных.
Изображение десятичных дробей на координатном луче
Как и обыкновенные дроби, десятичные дроби можно отметить на координатном луче.
Равные десятичные дроби изображаются на координатном луче одной и той же точкой.
Меньшая дробь лежит на координатном луче левее большей, а большая – правее меньшей.
Как читать десятичные дроби
В первую очередь обсудим вид десятичной дроби. Каждая цифра после запятой имеет своё название.
Десятые, сотые, тысячные, десятитысячные…
Десятые, сотые и тысячные
Попробуем прочитать десятичную дробь из примера выше. Чтобы правильно прочитать десятичную дробь нужно:
Прочитать число слева от запятой и добавить слово «целыx», так как слева от запятой находится целая часть десятичной дроби. Читаем: «сорок три целых».
Затем прочитать число справа от запятой: «семь тысяч пятьсот шестьдесят девять».
Значит, полное название дроби звучит так:
43,7569 — сорок три целых семь тысяч пятьсот шестьдесят девять десятитысячных.
Справа от запятой после самой последней правой цифры отличной от нуля можно добавлять сколько угодно нулей. От этого значение десятичной дроби не изменится.
Таким же образом если в конце десятичной дроби отбросить ноль, то мы получим такую же по значению десятичную дробь.
Нули можно добавлять (убирать) только после самой последней правой отличной от нуля цифры. Нули между цифрами в числе убирать нельзя.