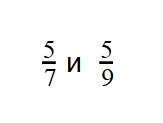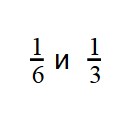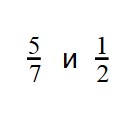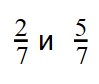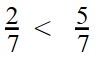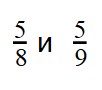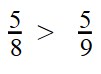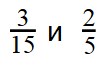что больше правильная или неправильная дробь
Правильные и неправильные дроби. Сравнение дробей
Если числитель дроби равен знаменателю, то дробь равна единице.
В буквенном виде этот вывод можно записать так:
$\frac
где m − натурально число.
А может ли возникнуть такая «неправильная» ситуация, когда числитель дроби окажется больше знаменателя?
Дробь, у которой числитель меньше знаменателя, называют правильной.
Дробь, у которой числитель больше знаменателя или равен ему, называют неправильной.
Этот пример иллюстрирует следующее свойство дробей.
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше, а меньше та, у которой числитель меньше.
Эти примеры иллюстрируют следующее свойство.
Все правильные дроби меньше единицы, а неправильные − больше или равны единице.
Это свойство позволяет сделать следующий вывод.
Каждая неправильная дробь больше любой правильной дроби, а каждая правильная дробь меньше любой неправильной дроби.
Отметим, что на координатном луче из двух дробей большая дробь расположена правее меньшей.
Этот пример иллюстрирует следующее свойство дробей.
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.
Правильные и неправильные дроби.
Виды дробей.
Как вы уже заметили дроби бывают разные. Например, \(\frac<1><2>, \frac<3><5>, \frac<5><7>, \frac<7><7>, \frac<13><5>, …\)
Делятся дроби на два вида правильные дроби и неправильные дроби.
В правильной дроби числитель меньше знаменателя, например, \(\frac<1><2>, \frac<3><5>, \frac<5><7>, …\)
В неправильной дроби числитель больше или равен знаменателю, например, \(\frac<7><7>, \frac<9><4>, \frac<13><5>, …\)
Правильная дробь всегда меньше единицы. Рассмотрим пример:
Единицу мы можем представить как дробь \(1 = \frac<3><3>\)
Знаменатели одинаковые равны числу 3, далее сравниваем числители.
Вопросы по теме “Правильные или неправильные дроби”:
Может ли правильная дробь быть больше 1?
Ответ: нет.
Может ли правильная дробь равна 1?
Ответ: нет.
Может ли неправильная дробь меньше 1?
Ответ: нет.
Пример №1:
Напишите:
а) все правильные дроби со знаменателем 8;
б) все неправильные дроби с числителем 4.
Решение:
а) У правильных дробей знаменатель больше числителя. Нам нужно в числитель поставить числа меньшие 8.
\(\frac<1><8>, \frac<2><8>, \frac<3><8>, \frac<4><8>, \frac<5><8>, \frac<6><8>, \frac<7><8>.\)
б) В неправильной дроби числитель больше знаменателя. Нам нужно в знаменатель поставить числа меньшие 4.
\(\frac<4><4>, \frac<4><3>, \frac<4><2>, \frac<4><1>.\)
Пример №2:
При каких значениях b дробь:
а) \(\frac<12>\) будет правильной;
б) \(\frac<9>\) будет не правильной.
Решение:
а) b может принимать значения 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11.
б) b может принимать значения 1, 2, 3, 4, 5, 6, 7, 8, 9.
Задача №1:
Сколько минут в часе? Какую часть часа составляет 11 мин.?
Ответ: В часе 60 минут. Три минуты составят \(\frac<11><60>\) часа.
Сравнение дробей, как правильно
Сравнение дробей с одинаковыми знаменателями
Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби.
Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:
Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше.
А теперь на примерах.
Пример 1. Сравните дроби:
Пример 3. Сравните дроби:
Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший знаменатель.
Давайте разберем наглядный пример сравнения дробей:
Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.
Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей. Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.
Сравнение дробей с одинаковыми числителями
Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями.
Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем.
А теперь наши любимые примеры. Погнали!
Пример 1. Сравните дроби:
Пример 3. Сравните дроби:
Сравнение дробей с разными числителями и разными знаменателями
Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями. Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.
Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.
Давайте потренируемся в сравнении дробей.
Пример 1. Сравните дроби:
При сравнении неправильных дробей, помните, что неправильная дробь всегда больше правильной.
Пример 2: Сравните дроби:
Вычитание смешанных чисел
Вычитание проходит гладко, когда уменьшаемое больше вычитаемого.
В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы».
При вычитании дробей действует тот же самый принцип: вычитаемое должно быть больше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.
Пример 1. Найдите разность:
Вычитаемая дробь меньше уменьшаемой
Пример 2.Найдите разность:
Если знаменатели одинаковые — больше та дробь, числитель которой больше.
Примеры для самопроверки
Теория — это, конечно, хорошо. Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.
Пример 1. Сравните дроби:
Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что
Пример 2. Сравните дроби:
Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше. Это значит, что
Пример 3. Сравните дроби:
Ответ: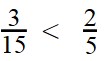
Какую дробь называют правильной в математике
Правильная дробь — что это такое в математике
Дробью в математике называют число, в состав которого входит одна либо несколько равных частей (или долей) от единицы.
Виды дробей в зависимости от формы записи:
Здесь число, которое расположено над чертой, является числителем. Под чертой расположен знаменатель. Числитель представляет собой делимое, а знаменатель играет роль делителя.
Правильная дробь — дробь с числителем, модуль которого меньше по сравнению с модулем знаменателя.
Неправильная дробь — дробь с числителем, модуль которого больше, чем модуль знаменателя, либо равен ему.
Любое число, которое является целым и не равно нулю, можно записать, как неправильную обыкновенную дробь. Знаменатель при этом будет равен 1.
Основное свойство дроби можно сформулировать таким образом: когда числитель и знаменатель, которые принадлежат одной дроби, умножают, либо делят на одно и то же число, дробь не поменяется, изменится лишь ее запись. К примеру:
1 5 = 1 × 2 5 × 2 = 2 10
Чем отличается правильная от неправильной и смешанной, как определить
Правильная дробь отличается тем, что имеет числитель, который меньше знаменателя.
В качестве наглядного примера можно записать правильные дроби:
Заметим, что во всех записанных случаях числитель меньше, чем знаменатель.
По сравнению с неправильной дробью правильная дробь всегда меньше 1. Тогда как неправильная дробь больше, либо равна 1.
Сравнение разных типов дробей:
Действия с правильными дробями, как найти
Правильные дроби можно встретить при решении множества задач по математике. Для них предусмотрены все действия, которые выполняют с обыкновенными дробями.
Приведение к общему знаменателю
Перед тем, как сравнить, сложить или вычесть дроби, требуется выполнить их преобразование. В результате арифметических действий дроби должны пробрести одинаковые знаменатели. К примеру, имеется пара дробей:
В результате знаменатели первой и второй дроби становятся одинаковыми и равными M. Допустимо заменить минимальное единое кратное при решении несложных примеров на какое-либо другое общее кратное. К примеру, таким кратным может стать произведение знаменателей.
Сравнение
С целью сравнения пары обыкновенных дробей необходимо выполнить операцию приведения их к единому знаменателю. Далее следует сравнить числители дробей, которые в итоге получились. Если числитель больше, то и дробь считается больше.
Далее необходимо привести дроби к знаменателю, равному 20.
3 4 = 15 20 ; 4 5 = 16 20
Сложение и вычитание
Прибавить одну обыкновенную дробь к другой обыкновенной дроби можно. Но перед этим требуется выполнить приведение этих дробей к единому знаменателю. После такой операции находят сумму числителей, а знаменатели оставляют без изменений.
1 2 + 1 3 = 3 6 + 2 6 = 5 6
НОК знаменателей для 2 и 3 составляет 6. Следует привести дробь 1 2 к знаменателю 6. Чтобы получить такой результат, необходимо выполнить умножение числителя и знаменателя на 3. В результате получим:
Затем требуется привести дробь 1 3 к аналогичному знаменателю. При этом нужно выполнить умножение числителя и знаменателя 2. Получим в итоге:
Похожий алгоритм действий предусмотрен для вычитания дробей. Перед тем, как посчитать их разность, следует привести дроби к общему знаменателю. Далее вычитают числители. Знаменатель при этом не меняется.
1 2 — 1 4 = 2 4 — 1 4 = 1 4
НОК знаменателей 2 и 4 составляет 4. Выполняя приведение дроби 1 2 к знаменателю 4, необходимо найти произведение числителя, знаменателя и числа 2. В результате получим:
Умножение и деление
При умножении двух обыкновенных дробей требуется выполнить умножение их числителей и знаменателей:
Рассмотрим частный случай умножения дроби на натуральное число. Для этого следует найти произведение числителя и данного числа, а знаменатель остается без изменений.
Когда числитель и знаменатель полученной дроби не являются взаимно простыми, необходимо такую дробь сократить:
5 8 · 2 5 = 10 40 = 1 4
В процессе деления одной обыкновенной дроби на другую требуется выполнить умножение первой дроби на дробь, которая является обратной для второй:
Возведение в степень и извлечение корня
Дроби можно возводить в степень. При этом необходимо выполнить арифметическое действие возведения в степень отдельно со знаменателем и числителем этой дроби:
2 3 3 = 2 3 3 3 = 8 27
Из дробей можно извлекать корень. Для того чтобы справиться с подобной задачей, необходимо извлечь заданный корень отдельно из числителя и знаменателя:
Перевод других видов дробей в правильную форму
Для того чтобы перевести неправильную дробь в правильную, либо для выполнения обратного действия, требуется соблюдать определенный порядок. Прямой перевод невозможен. Результатом подобной операции будет являться преобразованная запись, которая содержит в себе целую, а также дробную части. Последовательность действий:
С помощью достаточно простого метода удобно переводить числа из одной формы в какую-либо другую. Данный алгоритм можно записать в виде математического уравнения:
n a ÷ b = ( ( n × b ) + a ) ÷ b
Смешанное отношение представляет собой сумму из целого и части. Для того чтобы понять, как преобразовать дроби, следует выполнить сложение в качестве арифметического действия. В процессе первое слагаемое нужно записать в виде неправильной дроби путем деления целого на 1. Далее целесообразно воспользоваться правилом сложения дробей. Выполняется поиск общего знаменателя, дополнительных множителей, сложение в числителе. Формула имеет такой вид:
n a ÷ b = n ÷ 1 + a ÷ b = ( ( n × b ) + a ) ÷ b
Неправильную дробь превратить в обычную можно с помощью перевода ее в смешанную. В процессе выражение записывают в виде суммы натурального числа и правильной дроби:
Более простой способ преобразования дробей заключается в представлении делимого, как суммы дробей. При этом важно, чтобы при делении одной из них не было остатка:
m ÷ n = ( k + c ) ÷ n = k ÷ n + c ÷ n
Примеры задач с решением
В учебнике 100 листов. Ученик прочел ½ от общего количества страниц. Необходимо определить число листов, которые прочитал ученик.
Ответ: ученик прочитал 50 листов в учебнике.
Имеется емкость из стекла, наполненная водой, весом 550 гр. Половину воды вылили, а масса оставшейся составила 300 гр. Требуется рассчитать начальный вес воды и массу пустой емкости.
Значение массы воды, которую вылили:
250 гр. является половиной от всей воды, тогда вся вода весит:
Ответ: сначала в емкости было 500 гр. воды, массы емкости составляет 50 гр.
В кассе хранится сумма в 450 рублей. Необходимо определить количество денег в кассе после изъятия 1/3 от всей суммы.
Сравнение неправильных дробей правила и примеры.
Неправильные дроби сравниваем по тем же правилам, что и обыкновенные дроби или правильные дроби. Рассмотрим подробно эти правила.
Сравнение неправильных дробей с одинаковыми знаменателями.
Есть несколько правил сравнения неправильных дробей с одинаковыми знаменателями:
Рассмотрим пример:
Выполните сравнение неправильных дробей с одинаковыми знаменателями: а) \(\frac<20><13>\) и \(\frac<15><13>\) б) \(\frac<-161><57>\) и \(\frac<-98><57>\) г) \(\frac<17><3>\) и \(\frac<-11><3>\)
Решение:
а) Раз у дробей \(\frac<20><13>\) и \(\frac<15><13>\) одинаковые знаменатели переходим к сравнению числителей 20>15,
Сравнение неправильных дробей с одинаковыми числителями.
Пример:
Выполните сравнение неправильных дробей с одинаковыми числителями: а) \(\frac<21><9>\) и \(\frac<21><10>\) б) \(\frac<-15><3>\) и \(\frac<-15><4>\)
Решение:
а) У неправильных дробей с одинаковыми положительными числителями \(\frac<21><9>\) и \(\frac<21><10>\), та дробь больше, где знаменатель меньше 9 \frac<21><10>\)
б) У неправильных дробей с одинаковыми отрицательными числителями \(\frac<-15><3>\) и \(\frac<-15><4>\), та дробь больше где знаменатель больше 3 44, следовательно,
Сравнение неправильной дроби с правильной дробью.
Пример:
Сравните правильную дробь и неправильную дробь: а) \(\frac<14><13>\) и \(\frac<13><14>\) б) \(-\frac<27><6>\) и \(-\frac<17><18>\)
Решение:
а) Правильная и неправильная дробь положительны, поэтому неправильная дробь больше правильной дроби.
б) Правильная и неправильная дробь отрицательны, поэтому неправильная дробь меньше правильной дроби.
б) Неправильная дробь \(-\frac<4><3>\) отрицательна, поэтому \(0 1\)
Равные неправильные дроби.
Правило равных неправильных дробей:
Неправильные дроби равны тогда, когда при одинаковых знаменателях равны их числители. Например:
You may also like:
Сравнение рациональных чисел, определения и примеры.
Добавить комментарий Отменить ответ
Для отправки комментария вам необходимо авторизоваться.