что больше площадь круга или квадрата
Что больше? Площадь круга или квадрата( условия см. ниже)?
Сиреневый квадрат ABCD имеет периметр 40 см.
Окружность с центром в вершине квадрата B.
Данная задача несложная. Для её решения достаточно обладать базовыми знаниями геометрии: площадь квадрата и круга, периметр квадрата, теорема Пифагора, число П.
Зная периметр сиреневого квадрата АВСД находим его сторону.
Теперь можно найти площадь квадрата АВСД:
S=10^2=100 cм^2
Зная площадь жёлтого квадрата найдём его сторону.
Формула площади квадрата S=а^2, следовательно, сторона а=√S
Найдём диагонали квадратов по теореме Пифагора.
ДВ=√(10^2+10^2)=√200 =10√2 см.
Обозначу диагональ маленького квадрата Д1В1, тогда
Найдём разницу между диагоналями:
Разделив эту разницу пополам получим радиус окружности:
Формула площади круга S=пR^2, следовательно
S=3,14*(4√2)^2 =100,48 см.^2
100,48>100, следовательно площадь круга больше площади квадрата.
Определим радиус круга r=√(1^2+1^2)=√2.Опре делим площадь круга S=пи*r^2=пи*(√2)^2=2 пи.Ну и определим длину окружности С=2*пи*r=2*√2*пи.( По условиям задачи понятно что мы имеем там прямоугольный треугольник с катетами равными 1 и гипотенузой равной радиусу окружности)
Люблю решать такие задачки. Значит, дано: восемь плюс три минус четыре получится ноль.Теперь переложим одну спичку так, чтобы получилось равенство. Смотрите, где восемь, уберем одну спичку и добавим эту спичку к нулю. Вот какой результат мы видим теперь: девять плюс три минус четыре получится восемь. Это выглядит так: 9+3-4=8. (Извините, я не умею добавить рисунки.Поэтому пронумерую части цифры восемь:горизонтальны е сверху- вниз:a,b,c. Теперь вертикальные: слева-направо:d,k,l, m. Перетащим спичку-l).
Учительница стала балериной,девочка играет на гитаре и поет песни, квадратный глобус стоит на столу в углу, мальчик сидит с биноклем, в классе рядом с этим мальчиком за партой сидит дедушка и кушает, из пола растет кактус, позади дедушки сидит девочка, но не стуле, а на чурке, за этой девочкой сидит двое детей и читают книжки, в соседнем ряду сидит мальчик с зонтом, потому что идет дождь, за этим мальчиком сидит девочка на стуле, у которого нет ножек, на стене висят часы с тремя стрелками, рядом стоит аквариум, в котором вместо рыбок плавает сосиска, а вместо дверей железные двери как на корабле
Квадратура круга: наглядное доказательство
Словесные доказательства с трудом даются тем, кто привык мыслить визуально. Поэтому в математике так важна визуальная интуиция. Доказательства из таких пособий, как и «Евклид Начала: первые 6 книг» и «Доказательства без слов: учебник по визуальному мышлению» даются пониманию при взгляде на их страницы. Я рекомендую эти книги к прочтению каждому, кто интересуется доказательствами других математических проблем.
К примеру, мы помним из школьного курса, что площадь круга вычисляется по формуле π x r², но можем ли мы доказать, что эта формула справедлива для каждой возможной окружности?
Величайший из математиков Евклид нашёл доказательства этой формулы настолько простое, что теперь студенты изучают начала интегрального исчисления по нему. Евклид рассуждал так: круг можно поделить на четыре, шесть, шестнадцать, или бесконечно много равных частей, а потом расставить их так, чтобы получился прямоугольник.
Первое что нам нужно сделать — начертить окружность. Затем, мы разделим круг на 8 равных частей и расставим их в похожую на прямоугольник форму. Мы почти получили прямоугольник.
Повторим процесс, на этот раз с 32 равными частями. Если расставить их таким же образом как в предыдущем примере, то мы получим что-то ещё более похожее на прямоугольник.
Это значит, что если разделить круг на ещё больше равных частей — происходит удивительное, форма начинает приближаться к идеальному прямоугольнику.
Насколько много должно быть частей чтобы получить идеальный прямоугольник? Для этого его части должны быть бесконечно малыми — такими, что невозможно различить толщину, и стороны становятся почти вертикальными.
Таким образом, πr² может использоваться для вычисления площади любой из существующих окружностей.
Площадь круга
Для того чтобы найти площадь круга, существует формула, которую лучше запомнить:
S=πr 2 – это произведение числа пи на квадрат радиуса.
Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр 
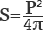
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два.
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель.
Данные онлайн калькуляторы предназначены для расчета площади круга. Вычисление происходит по приведенным выше геометрическим формулам, где π считается константой, округленной до 15-го знака после запятой.
Результат работы калькулятора также округляется до аналогичного разряда. Для использования калькулятора расчета площади круга необходимо ввести только значение радиуса, диаметра или окружности круга. Для калькулятора единицы измерения радиуса не имеют значения – результат вычисляется в абсолютном виде. То есть, если значение радиуса задано, например, в сантиметрах, то и вычисленное калькулятором значение площади круга тоже следует интерпретировать как представленное в квадратных сантиметрах.
Как определить площадь квадрата
Формула нахождения площади квадрата
Квадрат — это фигура, которая является частным случаем прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов. Способ вычисления всегда зависит от исходных данных. Чтобы узнать площадь квадрата, необходимо знать специальные формулы, рассмотрим пять из них.
Если известна длина стороны
Умножаем ее на то же число или возводим в квадрат.
Эту формулу проходят в 3 классе. Остальные формулы третьеклассникам знать пока не нужно, но они пригодятся ученикам 8 класса.
Если нам дана диагональ
Возводим ее в квадрат и делим на два.
S = d 2 : 2, где d — диагональ.
Если известен радиус вписанной окружности
Умножаем его квадрат на четыре.
Если у нас есть радиус описанной окружности
Возведем его в квадрат и умножим на два.
У нас есть дополнительные занятия по математике для учеников с 1 по 11 классы — записывайтесь!
Если есть периметр
Мы должны возвести его в квадрат и разделить на 16.
S = Р 2 : 16, где Р — это периметр.
Периметр любого четырехугольника равен сумме длин всех его сторон.
Популярные единицы измерения площади:
S квадрата. Решение задач
Мы разобрали пять формул для вычисления площади квадрата. А теперь давайте потренируемся!
Задание 1. Как найти площадь квадрата, диагональ которого равна 90 мм.
Воспользуемся формулой: S = d 2 : 2.
Задание 2. Окружность вписана в квадрат. Найдите площадь квадрата, если радиус окружности равен 24 см.
Если окружность вписана в квадрат, то сторона квадрата равна диаметру:
a = d
Диаметр окружности равен двум радиусам:
d = 2r
Получается, что сторона равна двум радиусам:
a = 2r
Используем формулу нахождения площади квадрата через сторону:
S = a 2
Так как из пункта 3 мы получили, что сторона равна двум радиусам, то формула площади квадрата примет вид:
S = (2r) 2
S = 4r 2
Теперь подставим значение радиуса в формулу площади:
S = 4 × 24 2 = 2304 см 2
Площадь
Что такое площадь
Понятие площади фигур рассматривается одним из разделов математики — конкретно, геометрией. Результат решения задач с нахождением площади геометрических фигур может использоваться для решения математических задач, в быту, в производстве.
Площадь фигуры — численная характеристика, которая передает информацию о размере геометрической фигуры.
Фигура, в математическом мире определяемая как множество точек на плоскости, должна быть ограничена со всех сторон, чтобы иметь понятие площади. Если фигура располагается на одной плоскости, она не имеет объема, а только площадь.
В самом простом случае, площадь фигуры можно посчитать по количеству клеток, которые она занимает. Подобным способом можно легко посчитать площадь квадрата, прямоугольника или прямоугольного равнобедренного треугольника.
Площадь в геометрии обозначается знаком S, от английского square — площадь.
Как математическая характеристика, площадь имеет четыре характеристики:
Единицы измерения площади
Площадь фигуры может измеряться в разных единицах в зависимости от поверхности, на которой располагается. Основной системой измерения считается Международная система единиц СИ.
Площадь измеряется в единицах измерения в квадрате:
В Древней Руси употребляли такие величины, как квадратная верста, десятина, квадратный сажень.
В античных источниках единицей измерения площади были актус, арура, центурия, югер.
Формула нахождения площади в математике
Существует множество формул нахождения площади простых геометрических фигур, которые зависят, в основном, от количества углов, сторон и их соотношений.
Площадь прямоугольника
Прямоугольником является геометрическая фигура, все углы которой равны 90°. При этом таких углов должно быть, как минимум три, а четвертый будет равен 90° в силу закона о сумме углов четырехугольника в евклидовой геометрии.
Вычисление площади прямоугольника будет происходить через умножение сторон:
где a и b являются сторонами прямоугольника.
Площадь квадрата
Квадратом является прямоугольник с равными сторонами. Все его углы равны 90°. Площадь квадрата можно найти сразу двумя способами:
По длине стороны:
Через диагонали:
где a — длина сторон квадрата;
d — длина диагоналей квадрата.
Площадь круга
Кругом является часть плоскости, которая лежит внутри окружности. Круг не имеет ни одного угла, а точки его окружности находятся на равном удалении от центра.
Площадь круга можно найти двумя способами:
Через радиус:
где π — постоянная Пи, равна 3,14.
Радиус, упоминаемый в формуле, является линией или отрезком, соединяющим центр и любую из точек окружности.
Через диаметр:
где π — постоянная Пи, равна 3,14.
Диаметр является отрезком, соединяющим две точки окружности и проходящим через центр. Он включает в себя два противоположно направленных радиуса.
Площадь эллипса
Эллипс является частным случаем окружности. Он, так же, как и круг, не имеет ни одного угла, но при этом точки окружности находятся на разном удалении от центра.
Найти площадь эллипса можно только одним способом: через произведение длин большой и малой полуосей эллипса и числа пи.
Площадь эллипса находится через произведение длин большой и малой полуосей эллипса и числа пи:
Площадь параллелограмма
Параллелограмм является геометрической фигурой с 4 углами и 4 сторонами, однако он отличается от прямоугольника по строению. Его противолежащие стороны попарно параллельны, а углы равны зеркально противолежащим.
Частными случаями параллелограмма являются квадрат, прямоугольник и ромб.
Найти площадь параллелограмма можно тремя способами:
Через сторону и высоту:
где a — сторона, к которой проведена высота,
h — высота непосредственно.
Через две стороны и величину угла между ними:
Через диагонали и угол между ними:
S = 1 2 × d 1 × d 2 × sin y
где d 1 и d 2 — это диагонали параллелограмма,
y — угол между ними.
Площадь ромба
Ромб, как частный случай параллелограмма, имеет те же свойства, кроме того, что все его стороны равны.
Площадь ромба также можно найти тремя способами:
По длине стороны и высоте:
Формула площади ромба по стороне и высоте выглядит так же, как и площадь параллелограмма по таким же характеристикам, с условием, что все высоты ромба будут равны:
По длине стороны и углу:
Формула площади ромба через длину сторон и углу между ними похожа на соответствующую формулу площади параллелограмма с условием того, что стороны равны, а значит, их перемножение можно заменить квадратом величины стороны:
По длине его диагоналей:
Площадь трапеции
Трапеция отличается от всех предыдущих фигур тем, что только две ее стороны, боковые, могут быть равны между собой. При этом они не параллельны. Две другие стороны параллельны, но не равны. Сумма углов трапеции равна 360°.
Площадь трапеции можно найти двумя способами:
По формуле Герона:
По длине основ и высоте:
Площадь треугольника
Треугольник является геометрической фигурой с тремя сторонами и суммой углов, равной 180°. По величине углов треугольники делятся на острые, тупые и прямоугольные. По числу равных сторон треугольники делятся на разносторонние, равносторонние и равнобедренные.
Площадь треугольника можно найти множеством способов:
По гипотенузе и острому углу:
a — любой из прилежащих острых углов.
Через сторону и высоту:
Через три стороны:
где р — полупериметр.
Через две стороны и угол между ними:
S = 1 2 × a × b × sin y
Через три стороны и радиус описанной окружности:
Через три стороны и радиус вписанной окружности:
где р — полупериметр.
Пояснения на примерах
Стены класса равны 7 и 5 метрам. Чему будет равна площадь пола в данной комнате?
Решение: S = 7 × 5 = 35
Ткань летучего змея порвалась. Вася решил сделать новую форму. Он посчитал, что длина жердей летучего змея равна 15 и 23 см. Форму какой площади нужно взять Васе с учетом того, что для припусков для пришивания нужно взять еще 2 см?
Равнобедренный треугольник имеет основание 4 дм и высоту 7 дм. Сколько будет его площадь?




