что больше одна третья или одна шестая

Что больше одна третья или одна шестая

В этой теме мы познакомимся с образованием долей, научимся их записывать, читать и сравнивать.

Доли появляются, если нам нужно разделить ЦЕЛОЕ на равные части, например, яблоко:

.

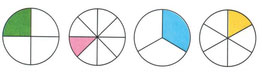
На доли можно разделить окружность:

Доля – это каждая из равных частей целого.

Название доли зависит от того, на сколько частей разделили целое.

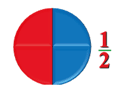
Половина

Например, яблоко разделили на две части, получилась половина яблока.

Любую долю можно записать как деление двух чисел. Мы разделили целое на две доли, каждую из долей мы можем записать в виде дроби, в которой черта обозначает знак деления.

Прочитать такую долю можно как ОДНА ВТОРАЯ.

Треть

Если целое разделили на три части, то получили ТРЕТЬ, третью часть.

Прочитать такую долю можно как ОДНА ТРЕТЬЯ.

Четверть

Если целое разделили на четыре части, получили ЧЕТВЕРТЬ, четвёртую часть.

Прочитать такую долю можно как ОДНА ЧЕТВЁРТАЯ.

Запись и чтение долей

одна пятая

одна шестая

одна восьмая

Сравнение долей

Для примера сравним две доли: одну шестую и одну третью.

Какая доля больше? Рассмотри рисунок:

Красным закрашены названные доли. Посмотри, какая доля больше? Одна третья.

Значит, одна третья часть БОЛЬШЕ, чем одна шестая часть.

Сравним ещё две доли: одну восьмую и одну четвёртую.

Какая доля больше? Рассмотри рисунок:

Красным закрашены названные доли. Посмотри, какая доля больше? Одна четвёртая.

Значит, одна четвёртая часть БОЛЬШЕ, чем одна восьмая часть.

Вывод: Чем долей больше, тем одна её часть МЕНЬШЕ.

Поделись с друзьями в социальных сетях:

Источник

Не знаете 1/6, 1/4 и 1/3 части алиментов — сколько это процентов? Ответ специалиста

Вопросы начисления алиментов остаются самыми болезненными для бывших супругов.

Все согласны с тем, что собственных детей нужно содержать, однако мнения разнятся, когда речь заходит о суммах. В данном материале речь пойдёт о выплате алиментов, установленных в долях от доходов.

Далее в статье мы рассмотрим алименты на ребенка 1/4 часть, третью и шестую — когда и в каких случаях удерживаются.

Дорогие читатели! Наши статьи рассказывают о типовых способах решения юридических вопросов, но каждый случай носит уникальный характер.

Условия начисления

В законодательстве выделяется несколько обстоятельств, на основании которых лицу может быть назначена выплата алиментов в долевом соотношении:

Если все три элемента есть, то выплаты могут быть назначены.

На видео смотрите более подробно про условия назначения алиментов:

1/2, 1/4 и 1/6 части — это сколько процентов и в каких случаях выплачиваются?

В статье 81 СК РФ законодательно закреплены величины, которые регулярно высчитываются из дохода плательщика:

Статья 81. Размер алиментов, взыскиваемых на несовершеннолетних детей в судебном порядке

При этом стоит отметить, что если от разных жен у вас двое детей, то в этом случае на каждого ребенка полагаются алименты в размере 16,5% или примерно 1/6 часть от зарплаты.

В данную категорию включаются:

Данные ставки не являются неизменными. На видео смотрите о том, кто и сколько должен платить:

Изменение размера долей алиментов

При разработке норм законодательства невозможно предусмотреть все нюансы семейных правоотношений. Поэтому суду частью 2 статьи 81 СК РФ предоставлено право уменьшать или увеличивать установленные доли в зависимости от обстоятельств.

Выделяется также несколько ситуаций, когда размеры перечисляемых алиментов могут быть пересмотрены в меньшую сторону:

Увеличен размер выплат будет в следующих ситуациях:

Статья 86. Участие родителей в дополнительных расходах на детей

Если деньги переводятся по решению суда, то изменение долей возможно только после пересмотра такого документа. Для этого заинтересованная сторона обращается с исковым заявлением, где мотивирует свою позицию.

В любом случае такие изменения остаются на усмотрение суда. Поэтому заявителю следует представить исчерпывающие доказательства.

Преимущества и недостатки этого вида начисления

Для обязанного лица можно найти несколько положительных характеристик при назначении алиментов в долевом исчислении:

Основной недостаток данного способа для получателя алиментов заключается в том, что обязанное лицо может договориться с недобросовестным работодателем, который будет выплачивать зарплату «в конверте».

Среди недостатков можно выделить следующие моменты:

Выплаты в твердой денежной сумме и в долях одновременно

В ситуациях, когда плательщики имеют низкий или непостоянный официальный доход, суду приходится устанавливать обязательную твёрдую денежную сумму, которая должна быть перечислена на содержание ребёнка, в сочетании с процентом от дохода родителя. Такая норма предусмотрена статьёй 83 СК РФ.

В описанной ситуации суд может назначить, например, сумму в размере 50% от установленного прожиточного минимума, но не менее 25% доходов обязанного лица, т.е. алименты в размере 1/4 части. Тогда при росте благосостояния плательщика увеличиться и материальная обеспеченность ребёнка. Судебная практика складывается таким образом, что подобные комбинированные ставки применяются при попытках сокрытия должниками своих расходов.

Стоит отметить, что в таком случае пересмотр установленных ставок не предусмотрен, в отличие от норм статьи 81 СК РФ. Следовательно, условия начисления алиментов останутся такими до совершеннолетия ребёнка (подробнее о том, до какого возраста ребенка могут взыскиваться алименты на его содержание, мы рассказываем в отдельной статье).

Алименты остаются наиболее часто используемым способом защиты материальных интересов несовершеннолетних. Плательщикам стоит помнить о том, что алименты они выплачивают не бывшим супругам, а детям, которым эти деньги нужны.

Об алиментах в твердой денежной сумме на видео:

Источник

Какой больше одна третия или одна шестая

1/3 больше чем 1/6. Сайт говорит, что должно быть больше символов

Другие вопросы из категории

№ 8, стр.5, 5-й пример.
В равенствах стёрлись знаки действий и числа. Помоги Незнайке вставить их.

Читайте также

двенадцатой; Одна шестая … одной двенадцатой; Одна треть … пяти двенадцатых; Три шестых … шести двенадцатых.

какая дробь больше 7/18 или 7/11

4: три целых четыре девятых плюс две целых шесть девятых. 5:две седьмых плюс одна целая пять седьмых. 6:десять целых две шестых минус три целых.

2) какое из чисел 135 или 155 кратно числу 15?
3) Сколько делителей имеет число 40? Назовите их.
4) Во сколько коробок можно разложить 20 карандашей так, чтобы их количество во всех коробках было одним и тем же?
5) Запишите двузначные числа, кратные 12.
6) Запишите три общих кратных чисел: 6и8, 2и5.
7) Найдите: (НОК 10;6) (НОК 3;15) (НОК 4:7)
8) Какие из чисел 5,9,13,15,21,33,43,61,81 являются простыми?
9) С помощью таблицы простых чисел определит, простыми или составным является число: 197, 389, 637, 853.
10) Какие из чисел 115, 120, 142, 170, 186:
Делятся на 2 и не делятся на 10;
Делятся на 2 и на 5?
11) Какие из чисел 138, 142, 261, 375, 801 делятся на:
на 3, на9.
12) Разложите на простые множители число: 300, 414.
13) Найдите частное и остаток от деления 80 на 7, запишите равенство, связывающее делимое, делитель, частное и остаток.
14) Найдите число, если известно, что при делении его на 8 в частном получается 12 и в остатке 6.
15) Сколько остатков и какие могут получаться при делении некоторого числа на 5?
16) Сто яиц для транспортировки нужно уложить в коробки. В наличии имеются коробки для 6 яиц. Сколько таких коробок потребуется?
ПОМОГИТЕ ХОТЬ С ОДНИМ!!

Источник

Сравнение дробей. Как сравнивать дроби с разными знаменателями?

Самая известная доля это половина. В жизни приставка пол встречается очень часто: полкилограмма, полкусочка, полчаса. Доли появляются, когда нужно целое разделить на равные части, допустим, полбуханки хлеба или полчаса.

Доля это каждая из равных частей единицы. Название доли зависит от того, на сколько частей разделили целое. Разделили на две части половина (Рис. 1).

Рис. 1. Половина целое, разделенное на две части

Если разделили на три это треть (Рис. 2).

Рис. 2. Треть целое, разделенное на три части

Разделили на четыре части четверть (Рис. 3).

Рис. 3. Четверть целое, разделенное на четыре части

Любую долю можно записать как деление двух натуральных чисел. Рассмотрим рисунок 4. Если целое разделили на две доли (синий рисунок), то тогда одну долю можно записать так: . Черта означает знак деления. Если разделили на три части (красный рисунок), то одну долю можно записать так: . Если целое разделили на четыре части (желтые рисунок), то тогда одну долю можно записать так: .

Рис. 4. Различные доли

Сведения из истории

Уже в древности люди пользовались долями. Для записи, например, в Китае использовали точку, чтобы обозначить долю (Рис. 5).

Рис. 5. Запись долей в Древнем Китае

А в Древнем Египте доли записывали, как показано на рисунке 6.

Рис. 6. Запись долей в Древнем Египте

Запись долей

Потренируемся записывать доли. Для того чтобы записывать доли, нужно выполнять действия по алгоритму.

Сначала надо посчитать, на сколько равных долей разделено целое, и записать это число под чертой.

Затем посчитать, сколько долей закрашено, и это число записать над чертой.

Задание 1

Рис. 7. Иллюстрация к заданию 1

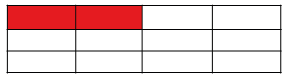
Посчитаем, на сколько частей разделен прямоугольник (рис. 7). Он разделен на пять частей, значит, число 5 запишем под чертой: . А закрашена всего одна часть, значит, над чертой запишем единицу: . Доля читается одна пятая.

Задание 2

Рис. 8. Иллюстрация к заданию 2

Данный прямоугольник разделен на девять частей (рис. 8), поэтому записываем под чертой количество равных частей: . Закрашена одна доля, значит, пишем сверху единицу: . Читается одна девятая.

Задание 3

Рис. 9. Иллюстрация к заданию 3

Прямоугольник разделен на десять частей (рис. 9). Записываем внизу десять: . Закрашена одна доля, пишем над чертой единицу: . Читается одна десятая.

Доли на Руси

Доли на Руси называли ломаными числами. В старинных инструкциях можно найти такое название долей:

(одна вторая) половина полтины.

(одна третья) треть.

(одна четвертая) четь.

(одна пятая) пятина.

(одна седьмая) седьмина.

(одна десятая) десятина.

Задание 4 (Сравнение долей)

В одном классе часть учеников занимается в музыкальной школе, учеников занимаются в спортивной школе, а учеников занимаются в художественной школе. Где занимается больше детей?

Обратим внимание на число, которое записано под чертой. Оно во всех трех долях одинаковое, потому будем сравнивать только те числа, которые стоят сверху, а там стоят числа 1, 2 и 4. Изобразим на рисунке (Рис. 10).

Рис. 10. Иллюстрация к решению задачи 4

По рисунку видно, что четыре доли это больше, чем две или одна. Поэтому делаем вывод: (больше, чем и ).

Пример

Рассмотрим три доли: , и . Если над чертой количество долей одинаковое, то будем сравнивать число, которое записано под чертой: 2 доли, 3 доли или 4 доли.

Рассмотрим рисунок 11. Записанные справа доли соответствуют отрезкам слева.

Рис. 11. Иллюстрация к примеру

Отрезок, соответствующий доле больше отрезка, соответствующего доле , а отрезок, соответствующий доле больше отрезка, соответствующего доле . Значит: . Делаем вывод: если наверху количество долей одинаковое, то чем меньше внизу число, тем доля больше.

Тренируемся записывать, читать и сравнивать доли.

Задание 5

На рисунке 12 круг разделен на шесть равных долей.

Рис. 12. Круг, разделенный на 6 долей

В первом круге взята одна доля, потому записываем , читаем одна шестая. Во втором круге взято четыре доли, записываем , читаем четыре шестых.

Вспоминаем правило: если под чертой числа одинаковые, то сравниваем числа над чертой. Четыре больше, чем один, ставим знак : , читается так: одна шестая меньше, чем четыре шестых.

Задание 6

Рассмотрим рисунок 13. Первый круг разделен на три части, возьмем одну часть, запишем: (одна треть). Второй круг разделен на четыре части, возьмем также одну часть и запишем (одна четвертая). Выясним, какая доля больше.

Рис. 13. Иллюстрация к заданию 6

Рассуждаем: если над чертой числа одинаковые, то сравниваем числа под чертой. Четыре больше, чем три (), а значит, долей больше и каждая доля меньше. Делаем вывод: .

Список литературы

Домашнее задание

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Половина

Половина — это самая известная доля.

Например, яблоко разделили на две части, получиласьполовина яблока.

Любую долю можно записать как деление двухчисел. Мыразделили целое на две доли, каждую издолеймы можемзаписать в виде дроби, в которой черта обозначает знак деления.

Прочитать такую долю можно как ОДНА ВТОРАЯ.

Треть

Если целое разделили на три части,то получили ТРЕТЬ, третью часть.

Прочитать такую долю можно как ОДНА ТРЕТЬЯ.

Четверть

Если целое разделили на четыре части, получили ЧЕТВЕРТЬ, четвёртую часть.

Прочитать такую долю можно как ОДНА ЧЕТВЁРТАЯ.

Запись и чтение долей

одна пятая

одна шестая

одна восьмая

Сравнение долей

Для примера сравним две доли: одну шестую и одну третью.

Какая доля больше? Рассмотри рисунок:

Красным закрашены названные доли. Посмотри, какая доля больше? Одна третья.

Значит, одна третья часть БОЛЬШЕ, чем одна шестая часть.

Сравним ещё две доли: одну восьмую и одну четвёртую.

Какая доля больше? Рассмотри рисунок:

Красным закрашены названные доли. Посмотри, какая доля больше? Одна четвёртая.

Значит, одна четвёртая часть БОЛЬШЕ, чем одна восьмая часть.

Вывод: Чем долей больше, тем одна её часть МЕНЬШЕ.

Сравнение дробей с одинаковыми знаменателями.

Если у двух дробей одинаковые знаменатели, то такие дроби сравнить просто.

Чтобы сравнить дроби с одинаковыми знаменателями, нужно сравнить их числители. Та дробь больше у которой больше числитель.

Сравните дроби (frac<7><26>) и (frac<13><26>).

Знаменатели у обоих дробей одинаковые равны 26, поэтому сравниваем числители. Число 13 больше 7. Получаем:

Если мы до решаем эти дроби, то получим числа(frac<20> <4>= 5) и (frac<20> <10>= 2). Получаем, что 5 > 2

В этом и заключается правило сравнения дробей с одинаковыми числителями.

Рассмотрим еще пример.

Сравните дроби с одинаковым числителем (frac<1><17>)и (frac<1><15>).

Так как числители одинаковые, больше та дробь, где знаменатель меньше.

Пример №2: Сравните правильную дробь с единицей?

Решение: Любая правильная дробь всегда меньше 1.

Задача №1: Сын с отцом играли в футбол. Сын из 10 подходов в ворота попал 5 раз. А папа из 5 подходов попал в ворота 3 раза. Чей результат лучше?

Решение: Сын попал из 10 возможных подходов 5 раз. Запишем в виде дроби (frac<5> <10>). Папа попал из 5 возможных подходов 3 раз. Запишем в виде дроби (frac<3> <5>).

Сравним дроби. У нас разные числители и знаменатели, приведем к одному знаменателю. Общий знаменатель будет равен 10.

Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на четыре части. пиццы больше, чем пиццы:

Каждый согласится с тем, что первая пицца больше, чем вторая.

Сравнение дробей с одинаковыми числителями

Следующий случай, в который мы можем попасть, это когда числители дробей одинаковые, но знаменатели разные. Для таких случаев предусмотрено следующее правило:

Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше. И соответственно меньше та дробь, у которой знаменатель больше.

Например, сравним дроби и . У этих дробей одинаковые числители. У дроби знаменатель меньше, чем у дроби .Значит дробь больше, чем дробь . Так и отвечаем:

Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на три и четыре части. пиццы больше, чем пиццы:

Каждый согласится с тем, что первая пицца больше, чем вторая.

Сравнение дробей с разными числителями и разными знаменателями

Нередко случается так, что приходиться сравнивать дроби с разными числителями и разными знаменателями.

Приведём дроби и к одинаковому (общему) знаменателю. Найдём наименьшее общее кратное (НОК) знаменателей обеих дробей. НОК знаменателей дробей и это число 6.

Теперь находим дополнительные множители для каждой дроби.Разделим НОК на знаменатель первой дроби . НОК это число 6, а знаменатель первой дроби это число 2. Делим 6 на 2, получаем дополнительный множитель 3. Записываем его над первой дробью:

Умножим дроби на свои дополнительные множители:

Мы пришли к тому, что дроби, у которых были разные знаменатели, превратились в дроби, у которых одинаковые знаменатели. А как сравнивать такие дроби мы уже знаем. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше:

Правило правилом, а мы попробуем разобраться почему больше, чем . Для этого выделим целую часть в дроби . В дроби ничего выделять не нужно, поскольку эта дробь уже правильная.

После выделения целой части в дроби , получим следующее выражение:

Теперьможно легко понять, почему больше, чем . Давайте нарисуем эти дроби в виде пицц:

2 целые пиццы и пиццы, больше чем пиццы.

Вычитание смешанных чисел. Сложные случаи.

Вычитая смешанные числа, иногда можно обнаружить, что всё идёт не так гладко, как хотелось бы. Часто случается так, что при решении какого-нибудь примера ответ получается не таким, каким он должен быть.

При вычитании чисел уменьшаемое должно быть больше вычитаемого. Только в этом случае будет получен нормальный ответ.

Уменьшаемое 10 больше вычитаемого 8, поэтому мы получили нормальный ответ 2.

А теперь посмотрим, что будет если уменьшаемое окажется меньше вычитаемого. Пример 57=2

В этом случае мы выходим за пределы привычных для нас чисел и попадаем в мир отрицательных чисел, где нам ходить пока рано, а то и опасно. Чтобы работать с отрицательными числами, нужна соответствующая математическая подготовка, которую мы ещё не получили.

Если при решении примеров на вычитание вы обнаружите, что уменьшаемое меньше вычитаемого, то можете пока пропустить такой пример. Работать с отрицательными числами допустимо только после их изучения.

С дробями ситуация та же самая. Уменьшаемое должно быть больше вычитаемого. Только в этом случае можно будет получить нормальный ответ. А чтобы понять больше ли уменьшаемая дробь, чем вычитаемая, нужно уметь сравнить эти дроби.

Например, решим пример .

Это пример на вычитание. Чтобы решить его, нужно проверить больше ли уменьшаемая дробь, чем вычитаемая. больше чем

поэтому смело можем вернуться к примеру и решить его:

Теперь решим такой пример

Проверяем больше ли уменьшаемая дробь, чем вычитаемая. Обнаруживаем, что она меньше:

В этом случае разумнее остановиться и не продолжать дальнейшее вычисление. Вернёмся к этому примеру, когда изучим отрицательные числа.

Смешанные числа перед вычитанием тоже желательно проверять. Например, найдём значение выражения .

Сначала проверим больше ли уменьшаемое смешанное число, чем вычитаемое. Для этого переведём смешанные числа в неправильные дроби:

Получили дроби с разными числителями и разными знаменателями. Чтобы сравнить такие дроби, нужно привести их к одинаковому (общему) знаменателю. Не будем подробно расписывать, как это сделать. Если испытываете затруднения, обязательно повторите действия с дробями.

После приведения дробей к одинаковому знаменателю, получаем следующее выражение:

Теперь нужно сравнить дроби и . Это дроби с одинаковыми знаменателями. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.

У дроби числитель больше, чем у дроби . Значит дробь больше, чем дробь.

А это значит, что уменьшаемое больше, чем вычитаемое

А значит мы можем вернуться к нашему примеру и смело решить его:

Пример 3. Найти значение выражения

Проверим больше ли уменьшаемое, чем вычитаемое.

Переведём смешанные числа в неправильные дроби:

Получили дроби с разными числителями и разными знаменателями. Приведем данные дроби к одинаковому (общему) знаменателю:

Теперь сравним дроби и . У дроби числитель меньше, чем у дроби , значит дробь меньше, чем дробь

А это значит, что и уменьшаемое меньше, чем вычитаемое

А это гарантировано приведёт нас в мир отрицательных чисел. Поэтому разумнее остановиться на этом месте и не продолжать вычисление. Продолжим его, когда изучим отрицательные числа.

Пример 4. Найти значение выражения

Проверим больше ли уменьшаемое, чем вычитаемое.

Переведём смешанные числа в неправильные дроби:

Получили дроби с разными числителями и разными знаменателями. Приведем их к одинаковому (общему) знаменателю:

Теперь нужно сравнить дроби и . У дроби числитель больше, чем у дроби . Значит дробь больше, чем дробь .

А это значит, что уменьшаемое больше, чем вычитаемое

Поэтому мы смело можем продолжить вычисление нашего примера:

Сначала мы получили ответ . Эту дробь мы сократили на 2 и получили дробь , но такой ответ нас тоже не устроил и мы выделили целую часть в этом ответе. В итоге получили ответ .

Задания для самостоятельного решения

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Что нужно знать о дробях прежде всего?

Как сделать изучение дробей наглядным?

Детям намного проще усваивать новое, если примеры будут наглядными. Самый доступный способ продемонстрировать принцип действия дробных чисел это еда. Прекрасно с этой целью справятся яблоки, плитка шоколада или торт. Разделите яблоко вместе с ребенком поровну на всех членов семьи.

Еще один замечательный способ наглядного изучения дробей детали конструктора. С их помощью ребенок может довольно быстро освоить простые примеры сложения и вычитания дробей, а также их сравнение.

Вполне доступным и увлекательным изучение дробей можно сделать с помощью аппликаций, рисунков и пластилина. Совместное творчество с регулярными комментариями прекрасный способ совместить приятное с полезным.

Как правильно познакомить ребенка с дробями?

Если вы решили помощь ребенку освоить дроби, не стоит сваливать на него всю информацию сразу. Ненавязчиво, понемногу, вооружившись доступными примерами из повседневной жизни, разговаривайте с ребенком о целых предметах и кусочках, о том, как из кусочков собрать целое и как из целого получается много-много частей.

Для начала объясните ребенку понятия часть и целое. Вот шоколадка, целая, вкусная. Она состоит из долек, кусочков, частей. Предположим, их 10. Малыш отломал кусочек и вот у него в руках 1 кусочек из 10. Отломал еще для мамы кусочек получилось уже два кусочка из 10. Регулярно повторяйте подобные эксперименты с пиццей, мандаринами или стаканом молока. Теория должна хорошенько закрепиться и усвоиться. Отрабатывать полученные знания на практике можно также на нашем сайте в блоке Обучение есть много интересных заданий по математике, с помощью которых ребенок может потренироваться в изучении частей и целого.

Далее можно приступать к объяснению понятия доли. Пусть ребенок разделит апельсин или шоколадку на равные части, чтобы всем хватило и никто не обиделся. Эти части называются доли. Доли это то, из чего состоит целый предмет. В шоколадке, состоящей из 10 равных кусочков, 10 долей. Если яблоко разрезать пополам, будет две доли, каждая из которых представляет собой половину целого яблока.

Когда ребенок достаточно успешно разберется в том, что такое часть, целое и доли, можно вводить понятие дробь и начинать дробить вместе с ним все, что попадется под руку: те же шоколадки или яблоки. Смысл самого процесса остается прежним. Дроби придумали для того, чтобы обозначать количество долей, взятых из целого и оставшихся в целом. Показатель под чертой (знаменатель) обозначает количество долей в целом предмете, а число над чертой (числитель) количество долей, которые мы хотим взять. То есть если у нас была шоколадка из 5 равных кусочков, а мы взяли 1, то дробь, выражающая это наше действие, выглядит как 1/5, а произносится как одна пятая (слово доля здесь опускается, но подразумевается).

Целый предмет тоже можно выразить через дробь. Для демонстрации этого отлично подойдет упаковка конфет. Коробочка целая, если в ней 10 конфет, каждая конфетка на своем месте. 10 конфет 10 частей, и целая упаковка 10 штук. Получается, что 10/10 это целая упаковка конфет, 1 упаковка. При изображении целого числа с помощью дроби числитель и знаменатель всегда одно и то же число, обозначающее все доли, составляющие целый предмет.

Таким образом, если ребенок уже умеет писать и готов учиться записывать дроби, постарайтесь постоянно напоминать ему последовательность, задавая наводящие вопросы. Сколько всего частей в целом предмете? Пишем под чертой. А сколько частей мы взяли из этого целого предмета? Пишем над чертой. Это довольно просто, если разобраться.

Когда ребенок активно знакомится с долями и целыми, он должен понимать, что дробные числа это не просто замысловатые математические задачки, а вполне обычное явление в повседневной жизни. Продемонстрируйте ему, что дроби пригодятся, например, когда малыш захочет поделить свои конфеты с другом. Расскажите, что дробями измеряют не только апельсины или торты, но и объемы жидкости, расстояние маршрута, деньги и даже время. Когда вы готовите ужин, гуляете в парке или путешествуете по гипермаркету со списком покупок в любой подходящей ситуации показывайте ребенку на живом примере, как работают дроби, для чего так необходимо в них разбираться и как их следует использовать. Понимая пользу и необходимость практического применения, детям будет интереснее и проще подружиться с такой непростой темой.

Автор: педагог-психолог Антонина Валевич

Источник