что больше квадрат суммы или сумма квадратов
Ввести с клавиатуры два числа. Определить, что больше: сумма квадратов или квадрат суммы этих чисел
Ввести с клавиатуры два числа. Определить, что больше, сумма квадратов или квадрат суммы этих чисел
Ввести с клавиатуры два числа. Определить, что больше, сумма квадратов или квадрат суммы этих.

Даны два числа. Если сумма или произведение этих чисел больше 100, то вычислить и напечатать.
Какова вероятность того, что сумма квадратов этих чисел больше 64?
два действительных числа x и y выбираются так что сумма их квадратов меньше 100 какова вероятность.
нажми F1 и прочитай.
function Sign(x: число): число;
Возвращает знак числа x
про case чуть больше:
Оператор выбора
Оператор выбора выполняет одно действие из нескольких в зависимости от значения некоторого выражения, называемого переключателем. Он имеет следующий вид:
case переключатель of
список выбора 1: оператор1;
.
список выбора N: операторN;
else оператор0
end;
Переключатель представляет собой выражение порядкового типа или строкового типа, а списки выбора содержат константы совместимого по присваиванию типа. Как и в операторе if, ветка else может отсутствовать.
Оператор case работает следующим образом. Если в одном из списков выбора найдено текущее значение переключателя, то выполняется оператор, соответствующий данному списку. Если же значение переключателя не найдено ни в одном списке, то выполняется оператор по ветке else или, если ветка else отсутствует, оператор case не выполняет никаких действий.
Список выбора состоит либо из одной константы, либо для перечислимого типа из диапазона значений вида a..b (константа a должна быть меньше константы b); можно также перечислить несколько констант или диапазонов через запятую. Например:
case Country of
‘Россия’: Capital := ‘Москва’;
‘Франция’: Capital := ‘Париж’;
‘Италия’: Capital := ‘Рим’;
else Capital := ‘Страна отсутствует в базе данных’;
end;
case DayOfWeek of
1..5: writeln(‘Будний день’);
6,7: writeln(‘Выходной день’);
end;
Списки выбора не должны пересекаться. Например, следующий фрагмент
case i of
2,5: write(1);
4..6: write(2);
end;
Сокращенное умножение: правила, формулы
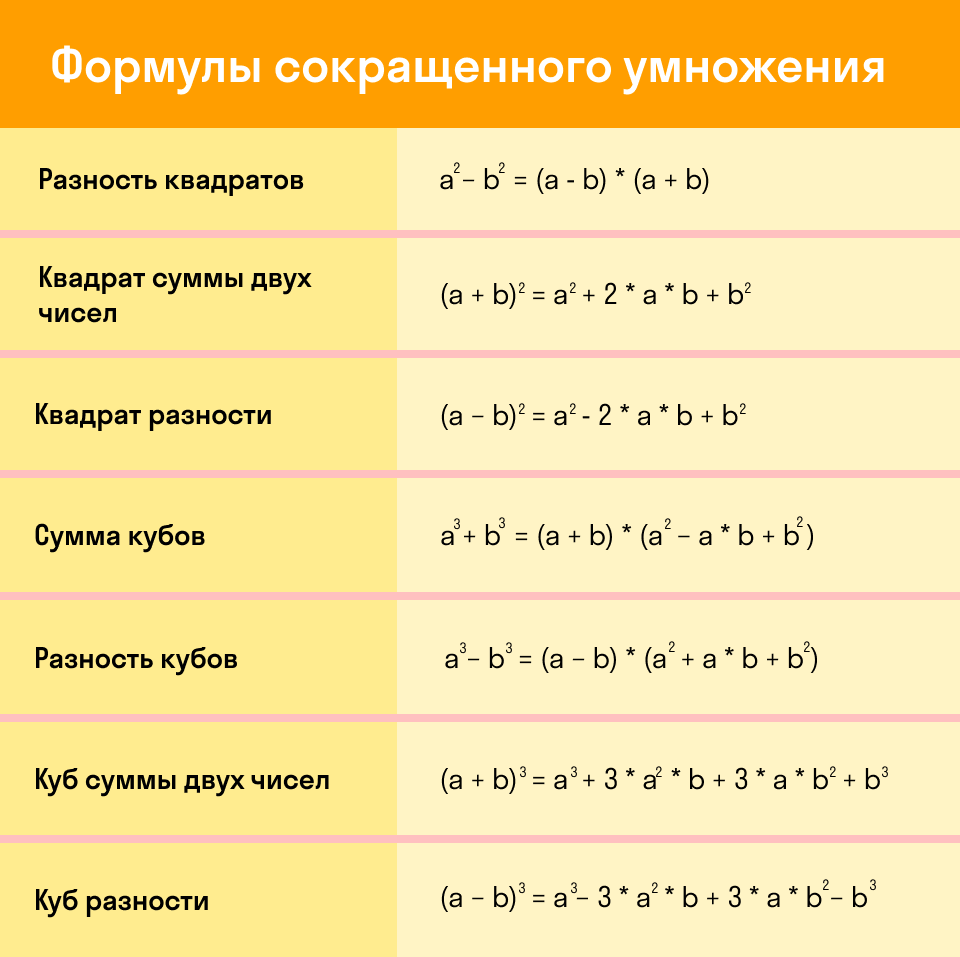
Формулы сокращенного умножения
Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.
Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.
Как читать формулы сокращенного умножения
Учимся проговаривать формулы сокращенного выражения:
Доказательство формул сокращенного умножения
Остальные ФСУ можно доказать аналогичным методом.
Дополнительные формулы сокращенного умножения
К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.
Бином Ньютона
Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:
Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:
ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.
Формула возведения в квадрат суммы трех, четырех и более слагаемых
Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два.
Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Формула разности n-ых степеней двух слагаемых
a n − b n = (a − b) * (a n-1 + a n-2 * b + a n-3 * b 2 + … + a * b n-2 + b n-1 ).
Для четных показателей можно записать так:
a 2*m − b 2*m = (a 2 − b 2 ) *(a 2*m−2 + a 2*m−4 * b 2 + a 2*m−6 * b 4 + … + b 2*m−2 ).
Для нечетных показателей:
a 2*m+1 − b 2*·m+1 = (a − b) * (a 2*m + a 2*m−1 * b + a 2*m−2 * b 2 + … + b 2*m ).
Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.
Решение задач
Давайте потренируемся и рассмотрим примеры с дробями.
Задание 1
Как решаем: воспользуемся формулой квадрата суммы: (55 + 10) 2 = 55 2 + 2 * 55 * 10 + 10 2 = 3025 + 1100 + 100 = 4225.
Задание 2
Что сделать: упростить выражение 64 * с 3 – 8.
Как решаем: применим разность кубов: 64 * с 3 – 8 = (4 * с) 3 – 2 3 = (4 * с – 2)((4 * с) 2 + 4 * с * 2 + 2 2 ) = (4 * с – 2)(16 * с 2 + 8 * с + 4).
Задание 3
Как решаем:
Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂