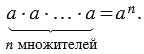что больше куба в математике
Степень числа. Квадрат и куб числа
Определение.
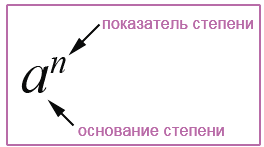
Степенью числа «
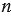
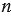

Например, найдем значение следующих степеней:
2 4 = 2





3 6 = 3














Например, найдем квадрат чисел 4 и 8:
4 2 = 4
8 2 = 8
Например, найдем куб чисел 5 и 7:
5 3 = 5


7 3 = 7


Степенью числа «
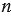
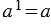
Сначала выполним возведение во 2 степень числа 4, затем находим значение выражения, находящегося в скобках, после чего выполняем умножение, и последним действием выполняем вычитание:
Поделись с друзьями в социальных сетях:
Кубы в математике
Проще всего разобрать этот вопрос на примере кубиков прессованного сахара-рафинада.
Вот есть у тебя один кубик сахара. Будем считать, что его объем — одна кубическая единица, один кубик.
Грань кубика — квадрат. Будем считать, что она имеет площадь в одну квадратную единицу.
При этом у кубика есть сторона какой-то длины. Будем считать, что длина стороны — одна единица.
А теперь представь, что тебе нужно из таких кубиков сахара сложить большой куб со стороной в две единицы.
Выкладываешь два кубика рядышком.
[_] [_]
Это ряд длиной в две единицы.
Теперь увеличим ширину, добавив еще один ряд:
[_] [_]
[_] [_]
Получился квадрат со стороной n = 2. Он состоит из n² = n • n = 4 кусочков.
Поэтому n² (вторую степень числа) называют квадратом. Эн в квадрате, или эн квадрат.
А теперь увеличим конструкцию в высоту — построим над этим квадратов еще один такой же квадрат, еще один «этаж».
Получится куб со стороной n = 2. Он состоит из n³ = n • n • n = 8 кусочков сахара.
Поэтому n³ (третью степень числа) называют кубом. Эн в кубе, или эн куб.
Если у тебя есть рафинад, то ты можешь потренироваться и построить куб со стороной n = 3 или n = 4, а затем посчитать, сколько тебе понадобилось мелких кубиков.
Только не ешь его много, а то живот заболит 🙂
Таблица кубов
Таблица кубов или таблица возведения чисел в третью степень. Интерактивная таблица кубов и изображения таблицы в высоком качестве.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 |
| 1 | 1000 | 1331 | 1728 | 2197 | 2744 | 3375 | 4096 | 4913 | 5832 | 6859 |
| 2 | 8000 | 9261 | 10648 | 12167 | 13824 | 15625 | 17576 | 19683 | 21952 | 24389 |
| 3 | 27000 | 29791 | 32768 | 35937 | 39304 | 42875 | 46656 | 50653 | 54872 | 59319 |
| 4 | 64000 | 68921 | 74088 | 79507 | 85184 | 91125 | 97336 | 103823 | 110592 | 117649 |
| 5 | 125000 | 132651 | 140608 | 148877 | 157464 | 166375 | 175616 | 185193 | 195112 | 205379 |
| 6 | 216000 | 226981 | 238328 | 250047 | 262144 | 274625 | 287496 | 300763 | 314432 | 328509 |
| 7 | 343000 | 357911 | 373248 | 389017 | 405224 | 421875 | 438976 | 456533 | 474552 | 493039 |
| 8 | 512000 | 531441 | 551368 | 571787 | 592704 | 614125 | 636056 | 658503 | 681472 | 704969 |
| 9 | 729000 | 753571 | 778688 | 804357 | 830584 | 857375 | 884736 | 912673 | 941192 | 970299 |
Таблица кубов
Теория
Куб числа – это результат умножения числа само на себя три раза. Операция вычисления куба числа – это частный случай возведения числа в степень, в данном случае в втретью:
Данное выражение читается: «возвести в куб число 6» или «6 в кубе».
Скачать таблицу кубов
Что такое куб: определение, свойства, формулы
В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).
Определение куба
Куб – это правильный многогранник, все грани которого являются квадратами.
Примечание: куб является частным случаем параллелепипеда или призмы.
Свойства куба
Свойство 1
Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.е.:
Свойство 2
Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.
Свойство 3
Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.
Например, на рисунке выше угол между гранями ABCD и AA1B1B является прямым.
Формулы для куба
Примем следующие обозначения, которые будут использоваться далее:
Диагональ
Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.
Диагональ грани
Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.
Площадь полной поверхности
Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.
Периметр ребер
Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.
Объем
Объем куба равен длине его ребра, возведенной в куб.
Радиус описанного вокруг шара
Радиус шара, описанного около куба, равняется половине его диагонали.
Радиус вписанного шара
Радиус вписанного в куб шара равен половине длины его ребра.
Таблица кубов и квадратов, как состовлять и найти
Как появилось понятие куб числа?
Древнегреческие математики оперировали так называемыми фигурными числами – числами, которые можно представить в виде фигуры. Выделялись, например:
Последовательность кубов натуральных чисел выглядит так
Полезно будет запомнить, хотя бы те, что меньше тысячи. Особенно мне нравится число 729. Посмотрите:
Еще несколько интересных свойств кубов чисел:
Вот так, к слову выглядит формула вычисления суммы первых кубов чисел:
Степень с натуральным показателем
Проще всего определяется степень с натуральным (то есть целым положительным) показателем.
Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.
Возвести число в куб — значит умножить его само на себя три раза.
Возвести число в натуральную степень — значит умножить его само на себя раз:
Теория
Куб числа – это результат умножения числа само на себя три раза. Операция вычисления куба числа – это частный случай возведения числа в степень, в данном случае в втретью:
Данное выражение читается: «возвести в куб число 6» или «6 в кубе».
Возвести в куб онлайн
Как возвести число в куб онлайн!? Введите нужное число, которое требуется возвести в куб и нажмите возвести в куб. Справа от равно появится число, которое возвели в куб
Ну и далее пробежимся по нескольким поисковым запросам, которые так или иначе вы задаете в строке поиска!
Дополнительная информация
Квадратом числа называют произведение двух одинаковых множителей.
Мы уже пробовали находить квадраты первого десятка натуральных чисел.
Возводить двузначные числа, трехзначные и т.д. числа немного сложнее, главное хорошо знать и помнить таблицу умножения чисел.
Существует способ быстрого возведения в квадрат двухзначных чисел, которые оканчиваются на цифру 5.
1) Первую цифру числа, возводимого в квадрат, необходимо умножить на сумму этого числа и единицы.
2) Записать полученное число- это будут первые цифры ответа (с этих цифр начинается ответ).
3) Ответ всегда будет заканчиваться на 25 (т.е. в конце ответа всегда будет стоять число 25).
4) Приписываем к числу, полученному в п 2, число 25, получаем ответ.
Рассмотрим поясняющий пример.
Найдем квадрат 65.
65 2 = 65 ∙ 65
6 ∙ (6 + 1) = 6 ∙ 7 = 42
Запишем число 42 и припишем к нему число 25.
65 2 = 4225
Проверим: Так как квадрат числа- это произведение двух одинаковых множителей 65 2 = 65 ∙ 65, то
65 2 = 65 ∙ 65 = 4225
Получили все тот же ответ: 65 2 = 4225