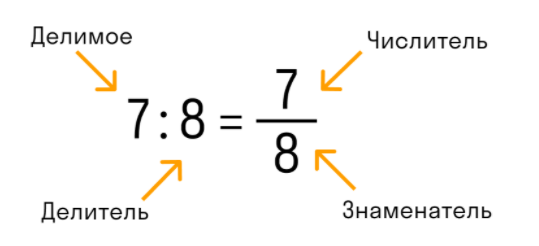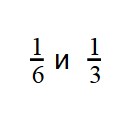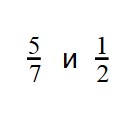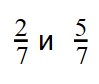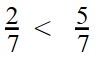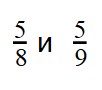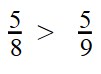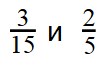что больше дробь или целое число
Дробь и натуральное число
Любое натуральное число можно представить в виде дроби – это дробь со знаменателем 1, потому что в знаменателе может стоять любое число.
Поэтому, можно говорить, что какой-то предмет (величина) неделимый, т.е. целый.
Числитель указывает, какое количество предметов мы берем, т.е. дробь вида а/1 — это натурального числа а. Значит, а/1 = а или а = а/1.
К примеру, число 32 – это обыкновенная дробь вида 32/1; а 15/1 = 15, 69 = 69/1.
Когда нам нужно сравнить обыкновенную дробь с натуральным числом, то можно: 1) сравнить две дроби, причем вторая имеет в знаменателе 1.
Затем нужно привести к общему знаменателю. А это очень долго и неэффективно!
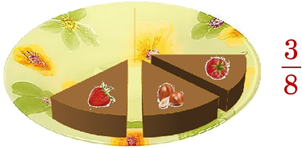
2) мы знаем, что если торт разрежем на несколько кусков, например, на 8
и возьмем 3 таких куска, то это будет 3/8 от торта. А это меньше, чем целый торт.
Значит, любая обыкновенная дробь всегда будет меньше целого, т.е. меньше 1.
Это правило можно использовать для сравнения двух разных дробей (см. статью здесь).
Например, 3/4 и 5/6.
Каждую из данных дробей сравниваем с единицей.
3/4 меньше единицы на 1/4, а 5/6 меньше на 1/6.
А 1/6 меньше, чем 1/4.
Т.е. у второй дроби меньше не хватает до единицы, чем у первой, значит, у первой больше не хватает до 1.
Поэтому 3/4
Средняя оценка 4.9 / 5. Количество оценок: 76
Сравнение десятичных дробей
Понятие десятичной дроби
Прежде чем мы расскажем, как сравнивать десятичные дроби, вспомним основные определения, виды дробей и разницу между ними.
Дробь — это число в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Ее записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это когда количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Основные свойства
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Правило сравнения десятичных дробей
Чтобы сравнить две десятичные дроби, сначала нужно сравнить их целые части. Если целые части равны, продолжаем искать первый несовпадающий разряд. Большей будет та дробь, у которой соответствующий разряд больше.
Вот так с первой строчки раскрыли тему сравнения десятичных дробей 😜 Но это еще не все — едем дальше.
Алгоритм сравнения десятичных дробей
Применим правило на практике. Сравним десятичные дроби: 15,7 и 15,719.
Целую часть с целой частью: 15 = 15. Целые части равны.
Десятые с десятыми: 7 = 7. Десятые также равны.
Чтобы сравнить две десятичные дроби, нужно уравнять количество знаков после запятой (приписать к одной из них справа нули), затем отбросить запятую, и сравнить два натуральных числа.
Сравним 3,656 и 3,48.
Сравнение дробей, как правильно
Сравнение дробей с одинаковыми знаменателями
Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби.
Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:
Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше.
А теперь на примерах.
Пример 1. Сравните дроби:
Пример 3. Сравните дроби:
Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший знаменатель.
Давайте разберем наглядный пример сравнения дробей:
Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.
Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей. Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.
Сравнение дробей с одинаковыми числителями
Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями.
Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем.
А теперь наши любимые примеры. Погнали!
Пример 1. Сравните дроби:
Пример 3. Сравните дроби:
Сравнение дробей с разными числителями и разными знаменателями
Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями. Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.
Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.
Давайте потренируемся в сравнении дробей.
Пример 1. Сравните дроби:
При сравнении неправильных дробей, помните, что неправильная дробь всегда больше правильной.
Пример 2: Сравните дроби:
Вычитание смешанных чисел
Вычитание проходит гладко, когда уменьшаемое больше вычитаемого.
В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы».
При вычитании дробей действует тот же самый принцип: вычитаемое должно быть больше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.
Пример 1. Найдите разность:
Вычитаемая дробь меньше уменьшаемой
Пример 2.Найдите разность:
Если знаменатели одинаковые — больше та дробь, числитель которой больше.
Примеры для самопроверки
Теория — это, конечно, хорошо. Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.
Пример 1. Сравните дроби:
Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что
Пример 2. Сравните дроби:
Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше. Это значит, что
Пример 3. Сравните дроби:
Ответ: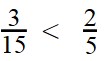
Онлайн калькулятор. Сравнение дробей.
Используя этот онлайн калькулятор для сравнения дробей, вы сможете очень просто и быстро сравнить две дроби.
Воспользовавшись онлайн калькулятором для сравнения дробей, вы получите детальное решение вашего примера, которое позволит понять алгоритм решения задач и закрепить пройденный на уроках материал.
Калькулятор сравнения дробей
Ввод данных в калькулятор сравнения дробей
В калькулятор сравнения дробей можно вводить: целые числа, десятичные дроби, обыкновенные дроби и смешанные числа.
Для ввода отрицательных чисел знак минус вводится в поле для целой части:
| или |
N.B. Буквенные выражения, операции извлечения корня и возведения в степень калькулятор не поддерживает!
Дополнительные возможности калькулятора сравнения дробей
Инструкция использования калькулятора сравнения дробей
Для сравнения дробей онлайн выполните следующие действия:
Правила. Сравнения дробей.
Чтобы сравнить две обыкновенные дроби, следует привести дроби к общему знаменателю и сравнить числители получившихся дробей. Дробь с большим числителем будет больше.
Смотрите также правила и примеры: сравнения дробей.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.