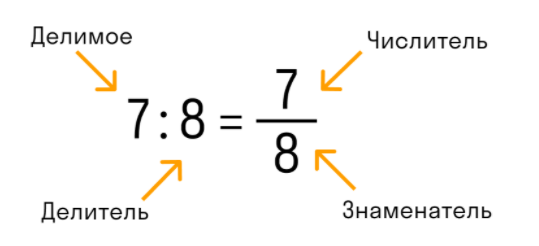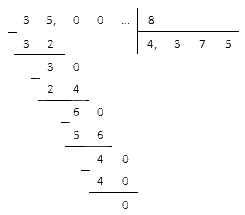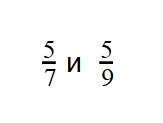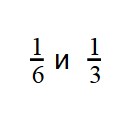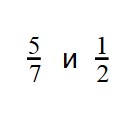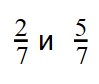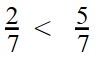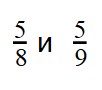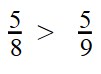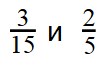что больше дробь или десятичная дробь
Сравнение десятичных дробей
Одно и то же натуральное число может быть представлено в виде обыкновенной дроби разными способами, например, 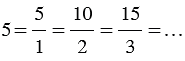
Если к десятичной дроби приписать справа какое угодно количество нулей, то получится дробь равная данной.
Пример:
Пример:
1) 3,40 = 3,4; 2) 0,50600 = 0,506; 3) 5,870000 = 5,87.
| Любое натуральное число можно представить в виде десятичной дроби с каким угодно количеством нулей после запятой. |
Пример:
| Из двух десятичных дробей с разными целыми частями больше та дробь, у которой целая часть больше. |
Пример:
1) 3,5 
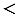
| Из двух десятичных дробей с одинаковыми целыми частями и равным количеством цифр после запятой больше будет та дробь, у которой больше первая (при чтении слева направо) из неодинаковых цифр их дробных частей (поразрядное сравнение). |
Пример:
1) 15,2 
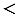

| Чтобы сравнить две десятичные дроби с равными целыми частями и различным количеством цифр после запятой, надо с помощью приписывания нулей справа уравнять количество цифр в дробных частях, после чего сравнить полученные дроби поразрядно (смотри правило выше). |
Пример:
Сравнить десятичные дроби 45,6 и 45,498.
Решение:
У дроби 45,6 одна цифра после запятой, а у дроби 45,498 три цифры после запятой, для того, чтобы сравнить данные дроби, приписываем к дроби 45,6 справа два нуля, получим новую дробь 45,600. Теперь поразрядно сравниваем дроби 45,600 и 45,498, получим 45,600 


Поделись с друзьями в социальных сетях:
Сравнение десятичных дробей
Понятие десятичной дроби
Прежде чем мы расскажем, как сравнивать десятичные дроби, вспомним основные определения, виды дробей и разницу между ними.
Дробь — это число в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Ее записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это когда количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Основные свойства
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Правило сравнения десятичных дробей
Чтобы сравнить две десятичные дроби, сначала нужно сравнить их целые части. Если целые части равны, продолжаем искать первый несовпадающий разряд. Большей будет та дробь, у которой соответствующий разряд больше.
Вот так с первой строчки раскрыли тему сравнения десятичных дробей 😜 Но это еще не все — едем дальше.
Алгоритм сравнения десятичных дробей
Применим правило на практике. Сравним десятичные дроби: 15,7 и 15,719.
Целую часть с целой частью: 15 = 15. Целые части равны.
Десятые с десятыми: 7 = 7. Десятые также равны.
Чтобы сравнить две десятичные дроби, нужно уравнять количество знаков после запятой (приписать к одной из них справа нули), затем отбросить запятую, и сравнить два натуральных числа.
Сравним 3,656 и 3,48.
Сравнение конечных и бесконечных десятичных дробей: правила, примеры, решения
В данной теме будет рассмотрена как общая схема сравнения десятичных дробей, так и детальный разбор принципа сравнения конечных и бесконечных дробей. Теоретическую часть закрепим решением типичных задач. Также разберем на примерах сравнение десятичных дробей с натуральными или смешанными числами, и обыкновенными дробями.
Внесем уточнение: в теории ниже будет рассмотрено сравнение только положительных десятичных дробей.
Общий принцип сравнения десятичных дробей
Для каждой конечной десятичной и бесконечной периодической десятичной дробей существуют соответствующие им некоторые обыкновенные дроби. Следовательно, сравнение конечных и бесконечных периодических дробей возможно производить как сравнение соответствующих им обыкновенных дробей. Собственно, это утверждение и является общим принципом сравнения десятичных периодических дробей.
На основе общего принципа формулируются правила сравнения десятичных дробей, придерживаясь которых возможно не осуществлять перевод сравниваемых десятичных дробей в обыкновенные.
То же самое можно сказать и про случаи, когда происходит сравнение десятичной периодической дроби с натуральными числами или смешанными числами, обыкновенными дробями – заданные числа необходимо заменить соответствующими им обыкновенными дробями.
Если же речь идет о сравнении бесконечных непериодических дробей, то его обычно сводят к сравнению конечных десятичных дробей. Для рассмотрения берется такое количество знаков сравниваемых бесконечных непериодических десятичных дробей, которое даст возможность получить результат сравнения.
Равные и неравные десятичные дроби
Равные десятичные дроби – это две конечные десятичные дроби, у которых равны соответствующие им обыкновенные дроби. В противном случае десятичные дроби являются неравными.
Теперь рассмотрим содержание понятия равных и неравных бесконечных периодических десятичных дробей.
Равные бесконечные периодические дроби – это бесконечные периодические дроби, у которых равны отвечающие им обыкновенные дроби. Если же соответствующие им обыкновенные дроби не равны, то заданные для сравнения периодические дроби также являются неравными.
Данное определение позволяет сделать следующие выводы:
Осталось рассмотреть равные и неравные бесконечные непериодические десятичные дроби. Такие дроби представляют из себя иррациональные числа, и их невозможно перевести в обыкновенные дроби. Следовательно, сравнение бесконечных непериодических десятичных дробей не сводится к сравнению обыкновенных.
Равные бесконечные непериодические десятичные дроби – это непериодические десятичные дроби, записи которых полностью совпадают.
Логичным будет вопрос: как сравнить записи, если увидеть «законченную» запись таких дробей невозможно? Сравнивая бесконечные непериодические десятичные дроби, нужно рассматривать только некоторое конечное число знаков заданных для сравнения дробей так, чтобы это позволило сделать вывод. Т.е. по сути сравнение бесконечных непериодических десятичных дробей заключается в сравнении конечных десятичных дробей.
Правила сравнения десятичных дробей. Решение примеров
Если установлен факт неравенства двух десятичных дробей, обычно также необходимо определить, какая из них больше, а какая – меньше. Рассмотрим правила сравнения десятичных дробей, которые дают возможность решить вышеуказанную задачу.
Очень часто достаточно лишь сравнить целые части заданных к сравнению десятичных дробей.
Та десятичная дробь, у которой целая часть больше, является бОльшей. Меньшей является та дробь, у которой целая часть меньше.
Указанное правило распространяется как на конечные десятичные дроби, так и на бесконечные.
Решение
В случае, когда целые части заданных к сравнению дробей равны, решение задачи сводится к сравнению дробных частей. Сравнение дробных частей производится поразрядно – от разряда десятых к более младшим.
Рассмотрим сначала случай, когда нужно сравнить конечные десятичные дроби.
Решение
В некоторых задачах на сравнение конечных десятичных дробей с разным количеством знаков после запятой необходимо к дроби с меньшим количеством десятичных знаков приписывать нужное количество нулей справа. Удобно уравнивать таким образом количество десятичных знаков в заданных дробях еще до начала сравнения.
Решение
Решение
Сравнивая бесконечные десятичные дроби, также применяют поразрядное сравнение, которое окончится тогда, когда значения в каком-то разряде у заданных дробей окажутся различными.
Решение
Решение:
Сравнение десятичных дробей с натуральными числами, обыкновенными дробями и смешанными числами
Чтобы получить результат сравнения десятичной дроби с натуральным числом, необходимо сравнить целую часть заданной дроби с заданным натуральным числом. При этом надо учесть, что периодические дроби с периодами 0 или 9 нужно предварительно представить в виде равных им конечных десятичных дробей.
Если целая часть заданной десятичной дроби меньше заданного натурального числа, то и вся дробь является меньшей по отношению к заданному натуральному числу. Если целая часть заданной дроби больше или равна заданному натуральному числу, то дробь больше заданного натурального числа.
Решение:
Решение
Решение
Чтобы произвести сравнение десятичной дроби с обыкновенной дробью или смешанным числом, необходимо:
— записать обыкновенную дробь или смешанное число в виде десятичной дроби, а затем выполнить сравнение десятичных дробей или
— записать десятичную дробь в виде обыкновенной дроби (за исключением бесконечной непериодической), а затем выполнить сравнение с заданной обыкновенной дробью или смешанным числом.
Решение
Решим задачу двумя способами.
Решение
Бесконечную непериодическую десятичную дробь нельзя представить в виде смешанного числа, но возможно перевести смешанное число в неправильную дробь, а ее, в свою очередь, записать в виде равной ей десятичной дроби. Тогда: 4 3 8 = 35 8 и
Сравнение дробей, как правильно
Сравнение дробей с одинаковыми знаменателями
Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби.
Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:
Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше.
А теперь на примерах.
Пример 1. Сравните дроби:
Пример 3. Сравните дроби:
Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший знаменатель.
Давайте разберем наглядный пример сравнения дробей:
Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.
Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей. Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.
Сравнение дробей с одинаковыми числителями
Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями.
Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем.
А теперь наши любимые примеры. Погнали!
Пример 1. Сравните дроби:
Пример 3. Сравните дроби:
Сравнение дробей с разными числителями и разными знаменателями
Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями. Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.
Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.
Давайте потренируемся в сравнении дробей.
Пример 1. Сравните дроби:
При сравнении неправильных дробей, помните, что неправильная дробь всегда больше правильной.
Пример 2: Сравните дроби:
Вычитание смешанных чисел
Вычитание проходит гладко, когда уменьшаемое больше вычитаемого.
В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы».
При вычитании дробей действует тот же самый принцип: вычитаемое должно быть больше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.
Пример 1. Найдите разность:
Вычитаемая дробь меньше уменьшаемой
Пример 2.Найдите разность:
Если знаменатели одинаковые — больше та дробь, числитель которой больше.
Примеры для самопроверки
Теория — это, конечно, хорошо. Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.
Пример 1. Сравните дроби:
Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что
Пример 2. Сравните дроби:
Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше. Это значит, что
Пример 3. Сравните дроби:
Ответ: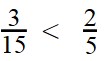
Сравнение конечных и бесконечных десятичных дробей, правила, примеры, решения.
В этой статье мы рассмотрим тему «сравнение десятичных дробей». Сначала обсудим общий принцип сравнения десятичных дробей. После этого разберемся, какие десятичные дроби являются равными, а какие – неравными. Дальше научимся определять, какая десятичная дробь больше, а какая меньше. Для этого изучим правила сравнения конечных, бесконечных периодических и бесконечных непериодических дробей. Всю теорию снабдим примерами с подробными решениями. В заключение остановимся на сравнении десятичных дробей с натуральными числами, обыкновенными дробями и смешанными числами.
Сразу скажем, что здесь мы будем говорить лишь о сравнении положительных десятичных дробей (смотрите положительные и отрицательные числа). Остальные случаи разобраны в статьях сравнение рациональных чисел и сравнение действительных чисел.
Навигация по странице.
Общий принцип сравнения десятичных дробей
В статье перевод обыкновенных дробей в десятичные дроби и обратно мы выяснили, что каждой конечной десятичной дроби и каждой бесконечной периодической десятичной дроби соответствуют некоторые обыкновенные дроби. Таким образом, сравнение конечных и сравнение бесконечных периодических десятичных дробей можно рассматривать как сравнение соответствующих им обыкновенных дробей.
Итак, общий принцип сравнения конечных и бесконечных периодических десятичных дробей таков: их сравнение по сути представляет собой сравнение обыкновенных дробей.
Исходя из этого принципа сравнения, выводятся правила сравнения десятичных дробей, позволяющие обойтись без перевода сравниваемых десятичных дробей в обыкновенные дроби. Эти правила, а также примеры их применения, мы разберем в следующих пунктах.
По схожему принципу сравниваются конечные десятичные дроби или бесконечные периодические десятичные дроби с натуральными числами, обыкновенными дробями и смешанными числами: сравниваемые числа заменяются соответствующими им обыкновенными дробями, после чего сравниваются обыкновенные дроби.
Что касается сравнения бесконечных непериодических десятичных дробей, то оно обычно сводится к сравнению конечных десятичных дробей. Для этого рассматривается такое количество знаков сравниваемых бесконечных непериодических десятичных дробей, которое позволяет получить результат сравнения.
Равные и неравные десятичные дроби
Сначала введем определения равных и неравных конечных десятичных дробей.
Две конечные десятичные дроби называются равными, если равны соответствующие им обыкновенные дроби, в противном случае эти десятичные дроби называются неравными.
Действительно, дописывание или отбрасывание в конце десятичной дроби нуля справа соответствует умножению или делению на 10 числителя и знаменателя соответствующей обыкновенной дроби. А мы знаем основное свойство дроби, которое гласит, что умножение или деление числителя и знаменателя дроби на одно и то же натуральное число дает дробь, равную исходной. Этим доказано, что дописывание или отбрасывание нулей справа в дробной части десятичной дроби дает дробь, равную исходной.
Переходим к определению равных и неравных бесконечных периодических десятичных дробей.
Две бесконечные периодические дроби равны, если равны отвечающие им обыкновенные дроби; если же соответствующие им обыкновенные дроби не равны, то сравниваемые периодические дроби тоже не равны.
Осталось разобраться с равными и неравными бесконечными непериодическими десятичными дробями. Как известно, такие десятичные дроби не могут быть переведены в обыкновенные дроби (такие десятичные дроби представляют иррациональные числа), поэтому сравнение бесконечных непериодических десятичных дробей нельзя свести к сравнению обыкновенных дробей.
Две бесконечные непериодические десятичные дроби равны, если их записи полностью совпадают.
Но есть один нюанс: невозможно увидеть «законченную» запись бесконечных непериодических десятичных дробей, следовательно, невозможно убедиться и в полном совпадении их записей. Как же быть?
При сравнении бесконечных непериодических десятичных дробей рассматривают лишь конечное число знаков сравниваемых дробей, которое позволяет сделать необходимые выводы. Таким образом, сравнение бесконечных непериодических десятичных дробей сводится к сравнению конечных десятичных дробей.
Неравенство бесконечных непериодических десятичных дробей при таком подходе устанавливается вполне определенно. Например, бесконечные непериодические десятичные дроби 5,6789… и 5,67732… не равны, так как очевидны различия в их записях (не равны конечные десятичные дроби 5,6789 и 5,6773 ). Бесконечные десятичные дроби 6,49354… и 7,53789… тоже не равны.
Правила сравнения десятичных дробей, примеры, решения
После установления факта неравенства двух десятичных дробей, часто нужно узнать, какая из этих дробей больше, а какая – меньше другой. Сейчас мы разберем правила сравнения десятичных дробей, позволяющие ответить на поставленный вопрос.
Во многих случаях бывает достаточно сравнить целые части сравниваемых десятичных дробей. Справедливо следующее правило сравнения десятичных дробей: больше та десятичная дробь, целая часть которой больше, и меньше та десятичная дробь, целая часть которой меньше.
Это правило относится как к конечным десятичным дробям, так и к бесконечным. Рассмотрим решения примеров.