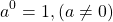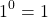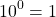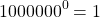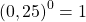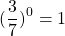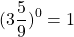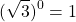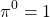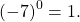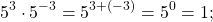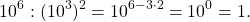число в нулевой степени чему равно и почему
Ноль в степени ноль
Ноль — наверное самое загадочное число и самое контринтуитивное. Ведь его аналога в реальной жизни просто нет. Ноль это отсутствие чего-то. Но почему ноль в степени ноль равняется единице? И главный вопрос, так ли это на самом деле? Можете проверить на своем калькуляторе до того, как прочтете…
Ноль «в степени» ноль
Как такое может быть? А вот как: 1 0 =1, 2 0 =1…. х 0 =1. Любое число при взведении в нулевую степени равняется единице. Чем сам ноль хуже? Но не все так просто. 
Что означает возвести в степень? Например «два в квадрате». Что мы делаем, мы двойку умножаем на саму себя 2 раза (2*2=4), «два в кубе», двойку умножаем саму на себя 3 раза (2*2*2=8). А что если степень, это «ноль»? Нужно взять число и умножить само на себя…. ноль раз? Это странно.
Вот как выглядит график функции y=x x
Видно, что при уменьшении значения Х значение У сначала снижается, а потом начинает расти и превращается… в единицу при условии очень маленьких (почти нулевых) значениях Х. Было бы логично предположить, что когда значение уменьшится до ноля, там тоже будет единица.
Еще раз, вернемся к простым цифрам:
Что означает эта запись? Чтобы получить девять, нужно тройку умножить два раза. Правда же?
Сколько раз нужно умножить тройку саму на себя, чтобы получить единицу? А если разделить 1 на 3? Простого ответа нет? Логично, что чем больше значение степени, тем больше результат, и чем меньше это значение, тем и результат меньше.
Но на графике выше показано, что кривая «упирается» в предел, в единицу. Точнее, значение функции становится равным 1, когда ноль еще даже не достигнут. И если уменьшать Х еще больше, все равно, дальше единицы не сдвинутся.
Контекст
Как получается, что при умножении ноля самого на себя получается что-то большее самого ноля?
Если мы в реальной жизни (а не в математике) съели все яблоки и их у нас 0, то сколько бы мы не умножали отсутствующие яблоки на такие же «нулевые» фрукты, как может у нас возникнуть целое яблоко? Если вам кажется такой вопрос простым, так и есть. С одной точки зрения это странное выражение будет равняться единице, а вот с другой оно будет «не определено». То есть никакой единицы а результате умножения ноля на ноль и быть не может, да?
Математика говорит, что:
3 2 ×3 2 это тоже самое, что и 3 2+2 = 3 4 = 3 × 3 × 3 × 3= 81
4 5 ÷4 3 это тоже самое, что и 4 5–3 = 4 2 = 4 × 4 = 16
Тогда, если степени одинаковы:
3 2 ÷3 2 это тоже самое, что и 3 2-2 = 3 0 = Ой?!
Но ведь мы можем и не вычитать степени, а просто сделать две операции отдельно:
3 2 ÷3 2 это тоже самое, что и 3 2-2 = 3 0 , но 3 2 =9, тогда 3 2 ÷3 2 = 3 2-2 или 3 2 ÷3 2 =9÷9=1
А что будет если одно число поделить на самого себя? Единица!
Матанализ
С точки зрения математического анализа, все одновременно и сложно, и совсем просто. Ноль в степени ноль = неопределенность. Что, согласитесь, более логично. Ведь если у нас нет ничего и мы ничего умножим само на себя, не может же возникнуть что-то из этой пустоты?
Теория множеств
Давайте посмотрим с точки зрения теории множеств. Допустим у нас есть два множества.
Первое множество, это количество символов пароля, которым закрыт доступ к вашей страничке в соцсети, или, еще лучше, PIN код банковской карты допустим — 4 символа.
Второе множество, это количество значений, корыте может принимать каждый символ. Предположим, что это только цифры, значит цифр — 10.
Вопрос, сколько вариантов комбинаций существует? Сколько раз нужно ввести случайную комбинацию, чтобы гадать пароль? Каждый символ
10 4 =10 000 тысяч вариантов.
Можно сказать, что множество цифр (10) отображается на множестве возможных символов (4). Но есть и «пустые» множества. Например, вы не поставили пароль вовсе, у вас ноль символов, так сколько попыток понадобится, чтобы получить доступ к счету? Ровно одна.
То есть при 10 0 =1, но тоже самое случится, если пароля нет и значений тоже нет 0 0 =1. Простыми словами, ноль в степени ноль, означает, что пароль не установлен и каждое значение тоже 0. Тогда может существовать только одна такая «комбинация».
А на самом деле?
Практического применения это математическое выражение, как нетрудно догадаться, не имеет вовсе. Ни одном инженеру, ни одному экономисту не придет в голову умножать ноль на ноль ноль раз. Это просто не применимая конструкция. Так что вопрос остается в области математики, и может быть философии.
Это наверное единственный случай, когда оставаясь математиком можно для свободно для себя решать чему равно «0 в степени 0».
Число в нулевой степени
Возведение в степень является одним из основных математических действий, без которых невозможны сложные расчеты. При этом отдельного рассмотрения заслуживает нулевая степень числа.
Возведение числа в нулевую степень
Известно, что при x 0 любое x равно 1 (x 0 = 1). Чтобы доказать это, нужно выяснить, откуда собственно взялся этот ноль?
Для этого вспомним формулы сложения и вычитания степеней.
7 3 = 7 2+1 = 7 2 × 7 1 = 7 × 7 × 7, ⇒
7 0 = 7 3-3 = 7 3 ÷ 7 3 = 1
Доказательство получено. Однако есть исключение из этого правила.
Парадокс нуля
Здесь все гораздо сложнее, но не настолько, чтобы не разобраться.
Известно, что 0 x = 0. Например: 0 4 = 0 × 0 × 0 × 0 = 0
Почему же мы часто встречаем выражение 0 0 = 1?
Подберем значения по табл.1.
Таблица 1. Функция ƒ(x) = x x
| x | x x |
| 1 | 1 |
| 0,9 | 0,909 |
| 0,8 | 0,836 |
| 0,7 | 0,779 |
| 0,6 | 0,736 |
| 0,5 | 0,707 |
| 0,4 | 0,693 |
| 0,3 | 0,697 |
| 0,2 | 0,725 |
| 0,1 | 0,794 |
| 0,01 | 0,955 |
| 0,001 | 0,993 |
Как видим, с определенного момента значение x x растет вместе с уменьшением x. В этом нет ничего сверхъестественного, это всего лишь пример действия формулы
Изобразим это на графике

Таким образом, делаем предположение, что это выражение является пределом.
Выразить это можно так:
Проверим, вычислив это значение.
Преобразуем основание выражения. Получаем:
x x = (e ln x ) x = e x ln x
Получаем следующее выражение:
Пользуемся правилом Лопиталя:
Официальная позиция современной математики гласит, что выражение 0 0 — представляет собой неопределенность, то есть не имеет точного значения.
Однако на практике, при расчетах, его значение подстраивается под конкретные требования. И чаще всего в этих случаях оно равно единице. Чтобы лучше разобраться с темой нулевой степени, советуем посмотреть видео ниже.
Степень 0
В алгебре возведение с нулевую степень встречается часто. Что такое степень 0? Какие числа можно возводить в нулевую степень, а какие — нет?
Любое число в нулевой степени, за исключением нуля, равно единице:
Таким образом, какое бы число ни возвели в степень 0, результат всегда получится одинаковый — единица.
И 1 в степени 0, и 2 в степени 0, и любое другое число — целое, дробное, положительное, отрицательное, рациональное, иррациональное — при возведении в нулевую степень дает единицу.
Единственное исключение — нуль.
Нуль в нулевой степени не определен, такое выражение не имеет смысла.
То есть в нулевую степень можно возводить любое число, кроме нуля.
Если при упрощении выражения со степенями получается число в нулевой степени, его можно заменить единицей:
Если при упрощении получается переменная или выражение с переменными в нулевой степени, пишем дополнительное условие — основание степени должно быть отличным от нуля:
Почему 0 в степени 0 равно 1?
Ноль в степени ноль является неопределенным выражением.
Это выражение может быть равно чему угодно в зависимости от скорости направления предельного перехода к нулю.
Однако, некоторые авторы предлагают принять соглашение о том, что 0^0=1. В пользу подобного варианта приводятся несколько доводов. Например, разложение в ряд экспоненты и другие.
Дискуссия по поводу определения продолжается, по крайней мере, с начала XIX века и ДО СИХ ПОР. В начале 19-го века математики считали, что 0^0=1, но в 1821 году Коши причислил 0^0 к неопределённостям, таким, как, например, 0/0.
Сайт MathWorld считает, что 0^0 считается неопределённым, несмотря на то, что соглашение 0^0=1 позволяет в некоторых случаях упростить запись некоторых формул. В России Большая российская энциклопедия, Большая советская энциклопедия, Математический энциклопедический словарь, Справочник по элементарной математике Выгодского, школьные учебники и другие источники однозначно характеризуют 0^0 как выражение, не имеющее смысла (неопределённость).
Интересно, что в компьютерных языках программирования, при использовании функции возведения в целую степень, 0^0 всегда дает результат равный 1. Но такой же результат будет не только для нуля, но и для NaN и для бесконечность. То есть, это чисто так устроена функция возведения в целую степень.
А вот функция возведения в нецелую степень уже дает результат NaN, то есть неопределенность.
А в тех языках программирования, где нет разделения функции возведения в степень на функцию для целого и вещественного показателя, там всё по разному. Например, в C++ выдает единицу.
Better Explained: Как понять ноль в нулевой степени?
Как мы можем повторить ноль нулевое количество раз и получить единицу? Всё дело в том, что наш подход к степени числа как к многократному умножению неверен. Нам нужно сменить парадигму. Давайте посмотрим, как мы привыкли воспринимать арифметические действия, и что они на самом деле из себя представляют.
Сложение
Как мы привыкли думать: это повторяющийся счёт
Как на самом деле: перемещение
Умножение
Как мы привыкли думать: это многократное сложение
Как на самом деле: масштабирование
Степень
Как мы привыкли думать: многократное умножение
Как на самом деле: рост с течением времени
Смотрим на арифметику как на преобразование
Отойдём на шаг назад. Как мы изучаем арифметику? Нас учат, что числа — это некое количество единиц; сложение — это прибавление одного количества единиц к другому количеству единиц (3+4 = 7), а умножение — это многократное сложение (2*3 = 2+2+2 = 6).
Очевидно, что эта модель восприятия неполноценна. Числа — это не просто единицы чего-то; гораздо лучше представлять их как некие точки с определённым положением на линии. Положение может быть отрицательным (-1), либо между другими числами (2²), либо в другом измерении (i).
Таким образом арифметика предстаёт перед нами как способ преобразовывать число. Сложение становится перемещением (+3 — это перемещение на 3 единицы вправо); умножение становится масштабированием (*3 — это увеличить число в три раза).
А что же такое тогда степень числа?
Познакомьтесь с Экпандотроном™
Это Экспандотрон 3000. Он выглядит как достаточно потрёпанная микроволновка, но вместо подогрева пищи она занимается ростом чисел. Просто положите число внутрь и проделайте несколько простых операций.
Вуаля! После звукового сигнала достаём наше новенькое готовое число. Например, мы хотим изменить 1 на 9. Что нам нужно сделать?
Что мы видим? Мы видим, как число начинает преобразовываться: 1; 1,1; 1,2. По окончании первой секунды оно уже выглядит как 3 и продолжает меняться: 3,1; 3,5; 4,0; 6,0; 7,5. И по окончании второй секунды оно превратилось в 9.
В математическом представлении Экспандотрон (или показательная функция) делает для нас следующее:
Например, 3 2 = 9/1. Основанием является то количество раз, в которое нам нужно вырастить число (х3), а степенью — количество времени (2). Формула типа 2 n означает «Используйте свой Экспандотрон на мощности х2 в течение n секунд».
Работу Экспандотрона мы всегда начинаем с 1, чтобы посмотреть, как он меняет одну единицу. Если мы хотим посмотреть, что случится с 3 в Экспандотроне, мы просто масштабируем конечный результат. Например:
Начните с 1 и умножьте на двойку в третьей степени: 1*2 3 = 1 * 2 * 2 * 2 = 8
Начните с 3 и умножьте на двойку в третьей степени: 3*2 3 = 3 * 2 * 2 * 2 = 24
Каждый раз, когда вы видите простую степень, вы начинаете с 1.
Идём к пониманию масштабирующего множителя
При умножении мы можем просто указать конечный масштабирующий множитель. Хотите число в 8 раз больше? Умножаем на 8. Готово.
Степени более капризны в обращении. Вот как они работают:
Вы: Хочу вырастить вот это число.
Экспандотрон: Ок, давай его сюда.
Вы: И насколько большим оно станет?
Экспандотрон: Пффф, без понятия. Давай посмотрим.
Вы: Посмотрим? Я думал, ты зна.
Экспандотрон: Тихо! Оно растёт! Растёт!
Экспандотрон: Готово! Это шедевр!
Это может звучать раздражающе неопределённо, но знаете, что? Большинство явлений природы заканчиваются неизвестно чем!
Как думаете, бактерия действительно планирует делиться каждые 14 часов? Нет, она просто питается забытым вами в холодильнике хлебом и растёт так быстро, как только может. Чтобы предсказать поведение этой бактерии, мы можем лишь использовать значения темпа её роста и длительности роста — и только потом мы получим конечное значение.
Иными словами, степень числа — это такой способ сказать «Начинаем с таких условий, изменяем их и смотрим, к чему мы придём». Этим и занимается наш Экспандотрон.
Идём к пониманию дробных степеней
Очень легко запутаться, если мы думаем о двойке в полуторной степени привычным способом — как о многократном умножении. Но в Экспандотроне всё просто: 1,5 — это всего лишь проведённое в нём время.
2 1,5 означает 1,5 секунды в машине, значит, этот рост окажется где-то между двукратным и четырёхкратным.
Умножение степеней
Что если мы захотим прогнать два цикла роста один за другим? Ну, например, мы используем машину в течение 2 секунд, а потом ещё 3 секунды на той же мощности:
Представьте самую обычную микроволновку. Разве это не будет самый обычный цикл длительностью в 5 секунд? Будет. Здесь происходит то же самое — раз уже мощность (основание) остаётся одинаковой, мы просто складываем время:
Квадратные корни
Продолжим. Предположим, мы выбрали мощность а и устанавливаем рост в течение 3 секунд:
Неплохо. Как будет выглядеть рост в течение половины этого времени? Логично, что 1,5 секунды.
А если мы проделаем то же самое два раза?
частичный рост * частичный рост = полный рост
Смотрим на это уравнение и видим, что «частичный рост» — это квадратный корень из значения полного роста. А если мы разделим время на три части?
частичный рост * частичный рост * частичный рост = полный рост
А вот и кубический корень! Это даёт нам интуитивное понимание того, почему деление степеней даёт нам корни: мы разбиваем время на равные доли.
Отрицательные степени
А как быть с отрицательными степенями? Отрицательные степени для нас будут значить обратный отсчёт во времени. Если движение вперёд во времени приводит нас к росту, движение назад, скорее всего, выльется в уменьшение числа.
Это значит следующее: «Секунду назад у нас была половина от текущего количества (1/2 1 ). Любой график экспоненциального роста строится именно так.
Выберите точку на шкале времени, например, 3,5 секунды (2 3,5 = 11,3). Через секунду мы удвоим наше количество (2 4,5 = 22,5). А секунду назад у нас была всего лишь половина от текущего количества (2 2,5 = 5,65).
Приходим к нулевой степени
Значит, масштабирующий множитель равен единице, значит, никаких изменений с нашим числом не происходит. Новое число будет равняться исходному числу, то есть (вы же помните, что исходное число у нас единица?) единице. Масштабирования не происходит.
Приходим к нулевому основанию
Приходим к нулевому основанию в нулевой степени
0 в степени 0 означает рост х0 в течение 0 секунд. Хоть мы и планировали аннулировать число, мы так и не запустили машину. Новое число равно исходному числу (то есть в наш Экспандотрон мы положили единицу), масштабирующий множитель тоже равен единице.
Конечно, Экспандотрона на самом деле не существует (а жаль!). Конечно, числа на самом деле не выстраиваются в линейку — они всего лишь один из множества способов взглянуть на мир.
По материалам очаровательной статьи на Better Explained.