число образующих n в отводе что такое
Расчёт количества структурных составляющих и фаз



Лабораторная работа № 6
ДИАГРАММА Fe–С И СТРУКТУРА ЖЕЛЕЗОУГЛЕРОДИСТЫХ СПЛАВОВ
Цель работы
Изучить теорию процессов, происходящих в железоуглеродистых сплавах при охлаждении и нагреве; научиться определять по диаграмме состояния Fe – С фазовые и структурные состояния сталей и чугунов.
Теоретические основы
Процесс кристаллизации сплавов и связанные с ним закономерности строения сплавов изучают по диаграммам состояния. Диаграммы состояния –это графические изображения, показывающие в условиях равновесия фазовый состав и структуру сплавов в зависимости от температуры и химической концентрации компонентов.
При очень медленном охлаждении сплавов, начиная с температуры жидкого состояния, все фазовые превращения в них протекают равновесно благодаря тому, что процессы диффузии успевают изменять химический состав взаимодействующих фаз в строгом соответствии с диаграммой состояния. Такое охлаждение принято называть равновесным. Сплавы же после такого охлаждения, соответственно, находятся в равновесном состоянии и характеризуются равновесной структурой.
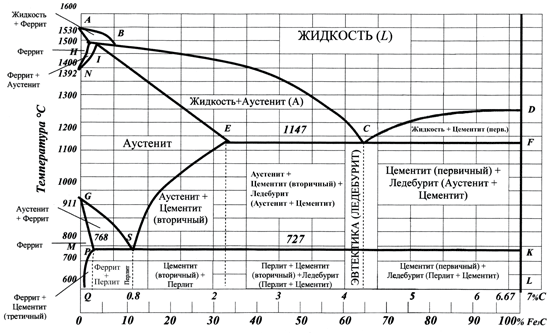
Стали и чугуны имеют в своем составе кроме железа и углерода и другие элементы – примеси, которые практически мало влияют на диаграмму состояния, поэтому для понимания процессов происходящих при нагреве и охлаждении сталей и чугунов, используется двойная диаграмма состояния Fe-С (железо – углерод). Полностью (до 100% углерода) диаграмма Fe-С не имеет практического применения, поэтому используется только часть диаграммы – до химического соединения Fe3C (цементит) (рис. 1.1.)
Рис. 1.1. Диаграмма состояния железо – углерод (Fe-С) или железо – цементит
Критические точки сплавов
Критическая точка – температура, при которой в сплаве происходят фазовые превращения. Критические точки определяют по кривым охлаждения сплавов.
В зависимости от характера превращения критические точки имеют собственные имена: ликвидус, солидус, сольвус (табл. 1.1) и др.
Каждая точка диаграммы состояния характеризует строго определенный состав сплава при соответствующей температуре. Точка А (1539 °С) отвечает температуре плавления железа, точка D (≈ 1250 °С) – температуре плавления цементита, точки N (1392 о С) и G (910 °С) соответствуют полиморфному превращению Feα↔Feγ.
Виды критических точек сплавов
| Название точки (обозначение) | Фазовое превращение при охлаждении (нагревании) | Примечания |
| Ликвидус | L↔ТВ Начало выпадения твердой фазы в жидком расплаве (конец расплавления твердой фазы) | Для чистых компонентов и эвтектических сплавов точки ликвидус и солидус совпадают |
| Солидус | L↔ТВ Конец выпадения твердой фазы в жидком расплаве (начало расплавления твердой фазы) | |
| Сольвус (точка вторичной кристаллизации) | ТВ↔ТВ + ТВII Выпадение вторичной фазы в результате снижении растворимости компонентов сплава в твердом состоянии | Вторичная фаза представляет собой химическое соединение АnBm |
| Точка Кюри (точка магнитного превращения) | Приобретение ферромагнитных свойств твердым веществом | Не связано с перекристаллизацией. Ni – 360 °C Fe – 768 °C Co – 1150 °C |
| Точка полиморфного превращения (точка перекристаллизации) | ТВa ↔ТВβ Переход высокотемпературной аллотропической формы в низкотемпературную (переход низкотемпературной аллотропической формы в высокотемпературную) | Для сплавов перекристаллизация проходит в интервале температур |
Концентрация углерода (по массе) для характерных точек диаграммы состояния следующая: В – 0,51% С в жидкой фазе, находя-щейся в равновесии с δ-ферритом (Feδ(C)) и аустенитом (Feγ(C)), при перитектической реакции и при 1499 о С; Н – 0,1% С в δ— феррите при 1490 о С; J – 0,16% C – в аустените-перитектике при 1490 о С; Е – 2,14% предельное содержание в аустените при 1147 °С; S – 0,8% С в аустените при реакции эвтектоидного превращения 727 °С; Р – 0,02% С – предельное содержание в феррите (Feα(C)) при 727 °С.
Линия, соединяющая точки АВСD на диаграмме, – линия ликвидус. Выше этой линии все железоуглеродистые сплавы находятся в жидком состоянии. Линия АHJECF – линия солидус. Ниже этой линии все сплавы находятся в твердом состоянии и при дальнейшем охлаждении происходят только процессы, связанные с изменением растворимости углерода в Feαи Feγ, а также процессы, которые обусловливаются аллотропическим (полиморфным) превращением железа.
Линия АВ указывает температуру начала кристаллизации δ- феррита из жидкого сплава; линия ВС – температуру начала кристаллизации аустенита; линия CD – температуру начала кристаллизации первичного цементита. При достижении температуры 1147°С ECF (эвтектики) состав жидкой фазы любого сплава, расположенного между точками E и F диаграммы, будет соответствовать точке C (4,3% С). При этой температуре оставшаяся часть жидкой фазы состава 4,3% углерода кристаллизуется с образованием эвтектики – механической смеси кристаллов аустенита и цементита, называемой ледебуритом.
Ниже линии GS происходит полиморфное превращение аустенита в феррит.
Линия SE является линией насыщения и показывает, как изменяется растворимость углерода Feγс изменением температуры. Вследствие уменьшения растворимости углерода в Feγпри понижении температуры из пересыщенного аустенита будет выделяться вторичный цементит ЦII.
Линия PSK 727 °C является линией эвтектоидного превращения. При этой температуре аустенит (Аs) состава точки S (0,8% C) распадается с образованием перлита (Пs): Аs→ Пs→ (Ф + Ц).
Значения точек на диаграмме железо – цементит
| Обозначение точки на диаграмме | Температура °С | Концентрация углерода % |
| А – температура плавления чистого железа | ||
| Н – предельная концентрация углерода в высокотемпературном феррите | 0.1 | |
| N – температура аллотропического превращения железа | ||
| D – температура плавления цементита | 6.67 | |
| Е – наибольшая концентрация углерода в аустените | 2.14 | |
| С – точка эвтектики | 4.3 | |
| G – температура аллотропического превращения железа | ||
| Р – предельная концентрация углерода в низкотемпературном феррите | 0.02 | |
| S – эвтектоидная точка | 0.8 |
Превращение в диаграмме Fe–Fe3C
Линия HJB характеризует перитектическое превращение (рис. 6.6), суть которого в том, что из жидкости концентрации т. В (0,5% С) и высокотемпературного феррита концентрации т. Н (0,1% С) образуется одна фаза – аустенит концентрации т. J (0,16% С).
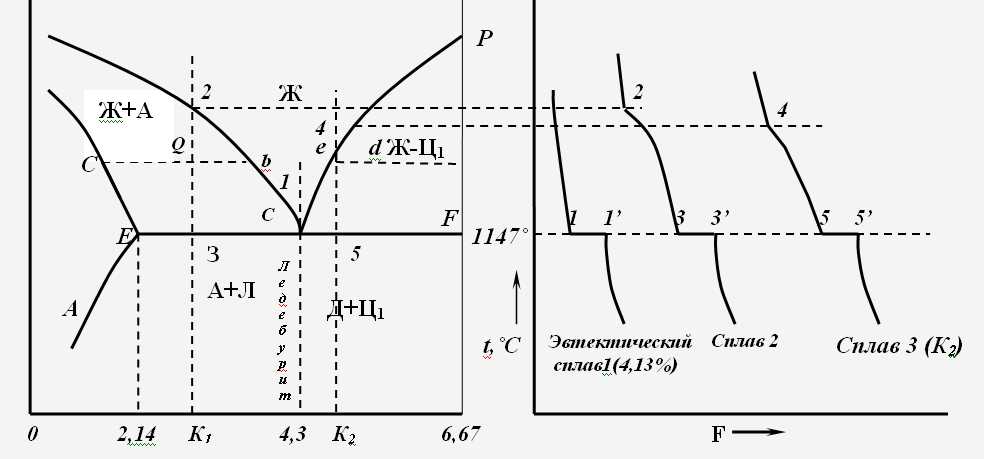
Линия ECF характеризует эвтектическое превращение (рис. 1.3), суть которого в том, что из жидкости концентрации т. С (4,3% С) кристаллизуется механическая смесь двух фаз – аустенита концентрации, т. Е (2,14% С) и цементита: Жс–Ае+Ц.
Эвтектическая механическая смесь носит название «ледебурит» и имеет концентрацию т. С (4,3% С). Как и все превращения, эвтектическое идет при остановке температуры (т.1–1) и заканчивается при кристаллизации всей жидкости.
Рис. 1.3. Область эвтектического превращения в диаграмме железо-цементит
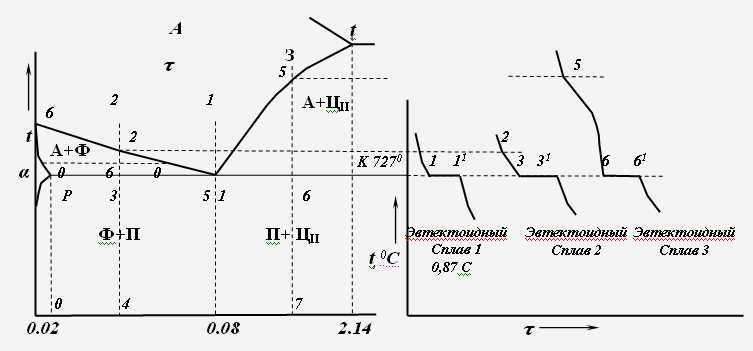
Линия PSK характеризует эвтектоидное превращение (рис. 1.4), суть которого в том, что из аустенита концентрации т. S (0,8% С) обра-зуется механическая смесь двух фаз – феррита концентрации т. Р (0,02% С) и цементита: А–Фр+ Ц.
Механическая эвтектоидная смесь носит название «перлит» и имеет содержание углерода 0,8%. Как правило, в равновесном состоянии в сталях перлит имеет пластинчатое строение (чередующиеся пластины феррита и цементита). Эвтектоидное превращение идет с остановкой температуры до исчезновения аустенита (рис. 1.4, сплав 1, т, 11′). Наиболее характерно образование эвтектоидной смеси перлита для сталей. Стали даже получили деление на эвтектоидные, доэвтектоидные и заэвтектоидные.
Рис. 1.4. Область эвтектоидного превращения в диаграмме железо-цементит
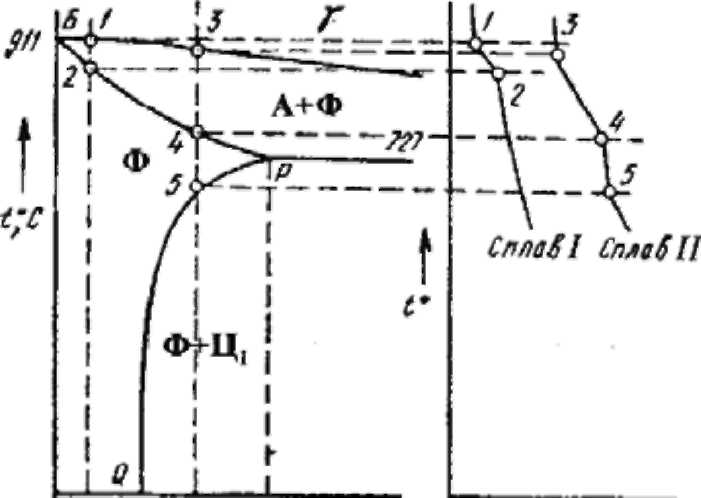
Как ранее было отмечено, в технически чистом железе находится не более 0,02% С, что и определяет специфику формирования его структуры. Из диаграммы Fe – Fe3C видно (рис. 1.5), что эвтектоидного превращения для такого рода сплавов не происходит. Из аустенита при охлаждении начинает выделяться феррит (сплав I, т.1–2; сплав II, т.3–4). Разница феррита и сплавов только в количестве растворенного углерода. Если углерода менее 0,01%, то структура феррита остаётся неизменной вплоть до комнатной температуры. Если же углерода более 0,01% и до 0,02%, то при пересечении при охлаждении линии PQ растворимость углерода в феррите падает (рис. 1.5, сплав II) и углерод выделяется по границам зёрен феррита в виде включений ЦΙΙΙ(цементита третичного).
Рис. 1.5. Ферритная область диаграммы Fe – Fe3C
Процесс выделения ЦΙΙΙ из феррита характерен для всех железоуглеродистых сплавов, имеющих в структуре феррит, просто его уловить в других структурах практически невозможно вследствие его объединения с другими видами цементита.
Последовательность образования равновесной структуры
На примере сплава, содержащего 0,5% С, рассмотрим последова-тельность протекания фазовых превращений, образующих в конечном счете равновесную структуру, предполагая его охлаждение с температур жидкого состояния равновесным. Схема кривой охлаждения показана на рис. 1.6. Итак, до температуры 1 следует простое охлаждение жидкого сплава. От точки 1, лежащей на линии ликвидуса, начинается образование кристаллов аустенита. Их количество растет и при температуре в точке 2 процесс кристаллизации заканчивается. Далее последует простое охлаждение зерен аустенита.



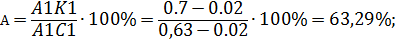
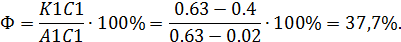
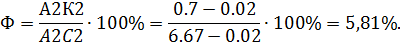
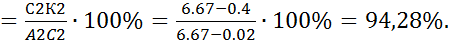


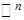 всех n-мерных векторов с целочисленными координатами с операцией сложения имеет стандартную систему образующих e =
всех n-мерных векторов с целочисленными координатами с операцией сложения имеет стандартную систему образующих e =  , где
, где  — вектор, у которого единственная ненулевая координата — i-ая, равная 1.
— вектор, у которого единственная ненулевая координата — i-ая, равная 1. .
.
 , составляющие систему образующих для аддитивной группы рациональных чисел R.
, составляющие систему образующих для аддитивной группы рациональных чисел R. .
.