число е в математике что это простыми словами
Экспонента в математике – это функция «y=ex», которая отражает непрерывный рост с коэффициентом. В этой функции «е» – это число Эйлера, которое представляет собой постоянную (
2,72). Говоря иначе, рост любой величины прямо пропорционален ее значению.
Допустим, мы слепили снежный ком и спустили его с горы. Он начинает катиться, одновременно наращивая объем. При этом чем больше он становится, тем выше скорость его движения. И наоборот: чем быстрее он катится, тем быстрее увеличивается в размерах. Получается, что масса и скорость снежного кома (y) экспоненциально возрастают со временем (x).
Экспонента в жизни. Экспоненциальный рост
Рассмотрим примеры экспоненты и экспоненциального роста в реальной жизни.
Вклад в банке под процент. У всех процессов, идущих по экспоненте, есть одна особенность: за одно и то же количество времени их параметры меняются одинаковое количество раз.
Например, вклад в банке каждый год увеличивается на определенное количество процентов. Если положить 1000 рублей в банк под 10% годовых, то через год вклад будет составлять 1100 рублей. А в следующем году 10% будут начисляться уже исходя из суммы в 1100 рублей. То есть, вклад вырастет сильнее, и так размер прироста будет увеличиваться из года в год.
Численность животных. Чем больше популяция животных, тем больше они размножаются. Соответственно, рост численности популяции прямо пропорционален количеству особей в ней.
Чем экспоненциальный рост отличается от линейного?
Линейный рост характеризуется стабильным прибавлением постоянной, а экспоненциальный рост – это следствие многократного умножения на постоянную. То есть если линейный рост на графике представляет собой стабильную линию, то экспоненциальный рост характеризуется быстрым взлетом.
В качестве примера можно привести обычную ходьбу. Если длина одного шага составляет 1 метр, то через 6 шагов человек преодолевает расстояние в 6 метров. Это и называется линейным ростом.
При экспоненциальном росте длина каждого шага в нашем примере увеличивается в 2 раза. То есть сначала человек шагает на 1 метр, потом на 2 метра, потом на 4 метра и так далее. В таком случае за 6 шагов можно пройти 32 метра, что гораздо больше, чем в предыдущем примере.
Экспонента и число е: просто и понятно.
Число e всегда волновало меня — не как буква, а как математическая константа. Что число е означает на самом деле?
Разные математические книги и даже моя горячо любимая Википедия описывает эту величественную константу совершенно бестолковым научным жаргоном:
Математическая константа е является основанием натурального логарифма.
Если заинтересуетесь, что такое натуральный логарифм, найдете такое определение:
Натуральный логарифм, ранее известный как гиперболический логарифм, является логарифмом с основанием е, где е – иррациональная константа, приблизительно равная 2.718281828459.
Определения, конечно, правильные. Но понять их крайне сложно. Конечно, Википедия в этом не виновата: обычно математические пояснения сухи и формальны, составляются по всей строгости науки. Из-за этого новичкам сложно осваивать предмет (а когда-то каждый был новичком).
С меня хватит! Сегодня я делюсь своими высокоинтеллектуальными соображениями о том, что такое число е, и чем оно так круто! Отложите свои толстые, наводящие страх математические книжки в сторону!
Число е – это не просто число
Описывать е как «константу, приблизительно равную 2,71828…» — это все равно, что называть число пи «иррациональным числом, приблизительно равным 3,1415…». Несомненно, так и есть, но суть по-прежнему ускользает от нас.
Число пи — это соотношение длины окружности к диаметру, одинаковое для всех окружностей. Это фундаментальная пропорция, свойственная всем окружностям, а следовательно, она участвует в вычислении длины окружности, площади, объема и площади поверхности для кругов, сфер, цилиндров и т.д. Пи показывает, что все окружности связаны, не говоря уже о тригонометрических функциях, выводимых из окружностей (синус, косинус, тангенс).
Число е является базовым соотношением роста для всех непрерывно растущих процессов. Число е позволяет взять простой темп прироста (где разница видна только в конце года) и вычислить составляющие этого показателя, нормальный рост, при котором с каждой наносекундой (или даже быстрее) всё вырастает еще на немного.
Число е участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов, и много-много других. Даже ступенчатые системы, которые не растут равномерно, можно аппроксимировать с помощью числа е.
Также, как любое число можно рассматривать в виде «масштабированной» версии 1 (базовой единицы), любую окружность можно рассматривать в виде «масштабированной» версии единичной окружности (с радиусом 1). И любой коэффициент роста может быть рассмотрен в виде «масштабированной» версии е («единичного» коэффициента роста).
Так что число е – это не случайное, взятое наугад число. Число е воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя.
Понятие экспоненциального роста
Давайте начнем с рассмотрения базовой системы, которая удваивается за определенный период времени. Например:
И выглядит это примерно так:
Деление на два или удваивание – это очень простая прогрессия. Конечно, мы можем утроить или учетверить, но удваивание более удобно для пояснения.
Математически, если у нас есть х разделений, мы получаем в 2^x раз больше добра, чем было вначале. Если сделано только 1 разбиение, получаем в 2^1 раза больше. Если разбиений 4, у нас получится 2^4=16 частей. Общая формула выглядит так:
Другими словами, удвоение – это 100% рост. Мы можем переписать эту формулу так:
Это то же равенство, мы только разделили «2» на составные части, которыми в сущности и является это число: начальное значение (1) плюс 100%. Умно, да?
Конечно, мы можем подставить и любое другое число (50%, 25%, 200%) вместо 100% и получить формулу роста для этого нового коэффициента. Общая формула для х периодов временного ряда будет иметь вид:
Это просто означает, что мы используем норму возврата, (1 + прирост), «х» раз подряд.
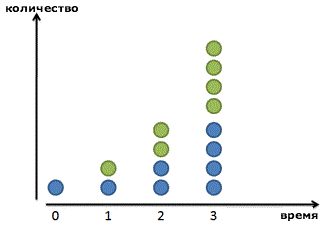
Наша формула предполагает, что прирост происходит дискретными шагами. Наши бактерии ждут, ждут, а потом бац!, и в последнюю минуту они удваиваются в количестве. Наша прибыль по процентам от депозита магическим образом появляется ровно через 1 год. На основе формулы, написанной выше, прибыль растет ступенчато. Зеленые точки появляются внезапно.
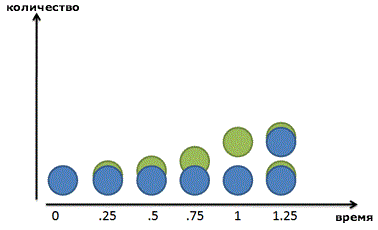
Но мир не всегда таков. Если мы увеличим картинку, мы увидим, что наши друзья-бактерии делятся постоянно:
Зеленый малый не возникает из ничего: он медленно вырастает из синего родителя. После 1 периода времени (24 часа в нашем случае), зеленый друг уже полностью созрел. Повзрослев, он стает полноценным синим членом стада и может создавать новые зеленые клеточки сам.
Эта информация как-то изменит наше уравнение?
Не-а. В случае с бактериями, полусформированные зеленые клетки все же не могут ничего делать, пока не вырастут и совсем не отделятся от своих синих родителей. Так что уравнение справедливо.
Но деньги меняют все
С деньгами дела обстоят по-другому. Как только мы зарабатываем пару монет прибыли, эти монетки начинают приносить свои микро-прибыли. Нет необходимости ждать, пока набежит целый рубль — свежим денежкам совсем не нужно дозревать, чтобы начать плодоносить.
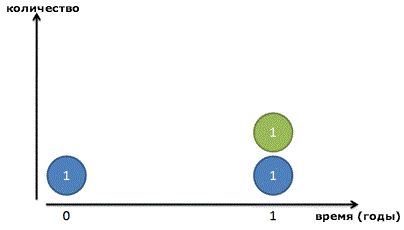
Основываясь на нашей старой формуле, прирост процента выглядит примерно так:
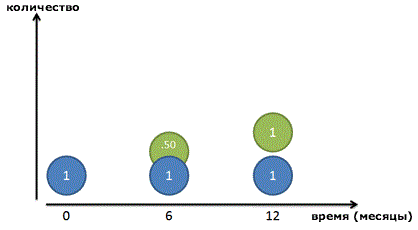
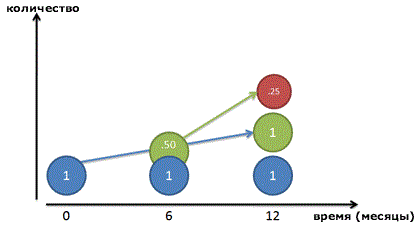
Но опять же, это не совсем правильно: вся сумма процента появляется в последний день. Давайте посмотрим поближе и разделим год на два промежутка. Мы зарабатываем 100% прибыль каждый год, или по 50% каждые 6 месяцев. Таким образом, мы заработаем 50 копеек в первые полгода, и другие 50 копеек во вторую половину года:
И все равно, это неверно! Конечно, наш рубль-родитель (Синий кружок) зарабатывает рубль в течение года. Но после 6 месяцев мы получим 50-копеечный кусочек прибыли – готовые деньги, которыми мы пренебрегаем! Эти 50 копеек уже могли бы зарабатывать свои собственные деньги:
Поскольку наш коэффициент равен 50% каждые полгода, эти 50 копеек могли бы заработать еще 25 копеек (50% от 50 копеек). В конце года мы бы получили:
Если все сложить, получится 2,25 рублей. Мы заработали 1,25 рубля всего на одном исходном рубле, и это даже лучше, чем удвоение!
Вернемся к формуле. Рост за два полу-периода по 50% составит:
Переходим на составной рост
Идем дальше. Давайте поделим рост не на два периода по 50%, а на 3 сегмента по 33% каждый. Кто сказал, что надо ждать целых 6 месяцев до начала получения прибыли? Давайте детализируем наши вычисления.
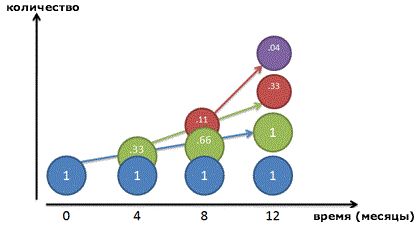
Вот так выглядит наш рост, расписанный на 3 составных периода:
Фуух! Спустя 12 месяцев у нас получается: 1 + 1 + 0.33 + 0.04 или примерно 2.37 рубля.
Потратим еще чуть времени, чтобы понять, что на самом деле происходит с таким ростом:
Теперь понятнее? Поначалу это сложно — я и сам запутался, пока рисовал все эти графики. Главное понять, что каждый «рубль» создает маленьких помощников, а те, в свою очередь, создают помощников себе, и так далее.
Если рассматривать год как 3 равных периода, формула роста будет такой:
рост = (1 + 100%/3) 3 = 2.37037.
Мы заработали 1.37 рубля, а это даже лучше, чем те 1.25, что получились у нас в предыдущий раз!
Можно ли преумножать деньги бесконечно?
А почему бы не разбить год на более короткие периоды? Как насчет месяца, дня, часа или даже наносекунды? Наша прибыль взлетит до небес?
Прибыль увеличится, но уже не намного. Попробуем подставить в нашу волшебную формулу разные значения n, и получим следующее:
Число Эйлера (e)
Число e (или, как его еще называют, число Эйлера) – это основание натурального логарифма; математическая константа, являющаяся иррациональным числом.
Способы определения числа e (формула):
1. Через предел:
Второй замечательный предел:
Альтернативный вариант (следует из формулы Муавра – Стирлинга):
2. Как сумма ряда:
Свойства числа e
1. Предел обратного числа e
2. Производные
Производной экспоненциальной функции является экспоненциальная функция:
Производной натуральной логарифмической функции является обратная функция:
3. Интегралы
Неопределенный интеграл натуральной логарифмической функции loge x:
Определенный интеграл от 1 до e обратной функции 1/x равен 1:
Логарифмы с основанием e
Натуральный логарифм числа x определяется как базовый логарифм x с основанием e:
Экспоненциальная функция
Это показательная функция, которая определяется следующим образом:
Формула Эйлера
Комплексное число e iθ равняется:
 eponim2008
eponim2008
Жизнь замечательных имен
Короткие истории о вещах и о людях, давших им свое имя
Что такое число Эйлера?

Число e столь же знаменито, сколь и число π . И столь же часто появляется оно в различных математических формулах. Вообще оба эти числа входят во множество формул в математике, физике, химии, биологии, в экономике. И всякий раз, когда они появляются, ученые, что называется «делают стойку», потому что знают: появление этих чисел всегда означает глубокую связь не только с законами математики, но и с законами природы.
Доказано, что число π связано с изотропностью пространства, а число e – с однородностью пространства и времени. Если перевести это на простой и понятный язык, то существование числа e означает, что законы природы неизменны в любом месте пространства, не изменялись во все времена и не изменятся в будущем. Существование же числа π означает, что все направления в пространстве одинаковы. Физики-теоретики, из этих важных положений о свойствах пространства и времени выводят важные законы сохранения, в том числе, закон сохранения энергии. А если уж взлететь совсем в эзотерические бездны, изотропность пространства в совокупности с однородностью пространства и времени накладывают запрет на существование Бога-создателя. Потому что такому Создателю, которого представляем мы, нет места в том пространстве-времени, которое мы пока что можем охватить разумом. Либо, если он существует, нарушаются основные законы мироздания, которые мы в данный момент считаем незыблемыми и на которых зиждется все наше знание о природе. Факт этот математически доказан.
Впрочем, сам Леонард Эйлер в Бога верил и даже, как говорят, дал укорот пламенному атеисту-энтузиасту Дени Дидро (Denis Diderot; 1713 — 1784). Тот, находясь при дворе Екатерины II, существование Создателя мира опровергал. Опровергал, как положено французу легкомысленно, но весело. Императрицу эти пустопорожние разговоры забавляли, но их идеологическую пагубность для своих подданных она прекрасно понимала. Посему Эйлеру было поручено возразить Дидро по-научному.
По-научному, так по-научному. Присутствуя на одной из бесед императрицы с Дидро, Эйлер заявил, что он знает математическое доказательство существования Бога и готов его тут же представить. Когда Дидро заинтересовался, Эйлер выдал ему какую-то математическую формулу, совершенно бессмысленную, после чего спросил у французского литератора, математики, конечно же, не знавшего, что он может на это возразить. Если бы Дидро к своему авторитету в глазах императрицы относился так же легкомысленно, как он относился к Богу, он мог бы отшутиться. Например, выдать Эйлеру какую-нибудь еще более бессмысленную формулу. Но против могучего танка по имени Леонард французские bon mot (остроты) оказались бессильными. Оторопь Дидро вызвала улыбки и смех, лицо выдающегося философа и богоборца было потеряно. Через несколько дней блестящий Денис покинул Санкт-Петербург.
Жаль, что во времена Дидро не существовало еще мобильных телефонов. Будь у Дидро такой приборчик, ему бы ничего не стоило связаться со своим коллегой по просветительским трудам, математиком и механиком Д’Аламбером и попросить совета. Ум хорошо, а два лучше. Глядишь, придумали бы какой-нибудь ответ суровому Эйлеру.
Впрочем, если бы тому всерьез захотелось представить доказательство бытия Божьего, он бы смог представить формулу, которую математики до сих пор считают самой красивой формулой своей науки. Эта формула называется тождеством Эйлера и выглядит следующим образом
В отличие от легковесных разговоров, эта формула, действительно, заставляет задуматься о глубоких взаимосвязях, существующих в мире и о причинах этих взаимосвязей. И удивиться, если не премудрости Создателя, то величию Природы. Что, в некотором смысле, одно и то же. В тождестве Эйлера соединены математический анализ (число e), геометрия (число π), алгебра (число i) и арифметика (число -1). Впрочем, Эйлер понимал, что говорить с Дидро о математике то же самое, что толковать с глухим о музыке. Поэтому в разговоре с французским гостем явно придуривался.
В начале рассказа Эйлер был назван великим русским ученым, хотя родился он в Швейцарии. Кому-то это может показаться странным. И напрасно! В 18-м веке Россия, без всякого сомнения, была империей. А в любой империи происхождение – вопрос второстепенный. Имперская идея расставляет подданных по местам, руководствуясь иными принципами.
Тем более, что большую часть своей жизни Л.Эйлер прожил в России. С мая 1727 года (то есть в возрасте 20 лет!) он прибыл в Санкт-Петербург и стал адъюнктом (помощником профессора) по отделению математики. Уже в следующем году Л.Эйлер бегло говорил по-русски. С тех пор до конца жизни он был связан с Санкт-Петербургской академией. Даже когда в 1741—1766 он был членом Прусской академии наук и поселился в Берлине, он оставался почетным русским академиком и принимал участие в ее работе. Все эти 25 лет место Эйлера было вакантным, но Академия Наук заполнить его кем-либо не считала нужным. А когда речь зашла о том, чтобы Эйлеру возвратиться в Санкт-Петербург, прусский император Фридрих II отпускать ученого со своей службы не желал, до тех пор, пока в этот вопрос не вмешалась лично Екатерина II.
Со времен пресловутой борьбы за национальные приоритеты (это было в начале 1950-х годов) сложилась стойкая легенда, о том, что Академия наук была «оккупирована» немцами, а национальный герой Михайла Ломоносов вовсю воевал с немецким засилием. Эта славная картина довольно далека от истины. Начать с того, что наукам и ремеслам Михаил Ломоносов (1711 —1765) обучался в Германии, в Марбургском университете в 1736—1739 годах.
Во-вторых, немецкие профессора, приглашенные в Россию, за редким исключением занимались своим делом не только в высшей степени профессионально, но и с большим энтузиазмом. Приглашение в Россию они не рассматривали, как приглашение к бездельному и сытому существованию среди русских снегов. Напротив, поездка в Россию была для них сравнима с переездом, который многие советские ученые в конце 1950-х – начале 1960-х годов совершили из больших столичных городов в Новосибирск, в юный Академгородок. Это была прекрасная возможность заниматься любимым делом, наукой, которое, к тому же оплачивалось гораздо лучше, чем в переполненной профессорами Европе. Характерно, что большая часть немецких ученых приезжала в Петербург, как Леонард Эйлер, людьми молодыми и полными сил. В России они приобрели опыт и научную известность. В России очень часто и оставались на всю жизнь. Для того, чтобы слыть русскими, чего же более надо?
В-третьих, немецкие ученые щедро делились своими знаниями с русскими коллегами. Леонард Эйлер, например, воспитал первых русских академиков: математика С. К. Котельникова и астронома С. Я. Румовского. И, кстати, М.В.Ломоносова Л.Эйлер не гнобил. В 1747 году он дал хвалебный отзыв (правда, формальный) на его работы по физике и химии. Сожалея, при этом, что достопочтенный Михаил Ломоносов высшей математикой не владел.
Научное наследие Леонарда Эйлера не велико, а просто огромно. Его работы способствовали созданию современного математического анализа, дифференциального и интегрального исчисления. Он создал новую математическую науку, вариационный анализ. Продолжая работы П.Ферма, он создал теорию чисел. Математик академик Н. Н. Лузин отмечал, что добрая половина того, что преподаётся в современных курсах высшей математики, основано на трудах Эйлера.
При этом Эйлер не был «чистым» математиком. Он работал также в области астрономии, гидродинамики, теоретической механики, оптики, кораблестроения, и даже теории музыки.
Не мудрено, что список различных математических понятий, носящих имя Л.Эйлера, занимает несколько страниц. Впрочем, то, что самый главный эпоним – это число Эйлера, e, постоянно встречающееся на страницах научных трудов по математике и физике. Эта важнейшая константа, основание натуральных логарифмов, было известно до Эйлера, однако он настолько глубоко и полно ее исследовал, что она носит его имя. И даже обозначается первой буквой его фамилии (Euler).
Обозначение основания натуральных алгоритмов именно буквой e вначале было случайным. Дело в том, что a, b, c и d были уже широко задействованы, и буква e оказалась первой «свободной» буквой. Неплохо было и то, что с этой буквы начиналось слово «exponential» («показательный», «экспоненциальный»).
Л.Эйлер тоже использовал букву e в своих трудах для обозначения основания натуральных логарифмов. При этом он, конечно, не думал о том, чтобы прославиться. Но так уж получилось, что последующие поколения математиков прочно связали пятую букву латинского алфавита с фамилией великого математика.
Для тех, кому урок, данный Эйлером Дидро, пошел впрок, дадим немного конкретных знаний.
Основание натуральных логарифмов, число e=2.718281828459045. Равенство всегда будет приблизительным, поскольку число это иррациональное (то есть, не представимо в виде обычной дроби, как частное от деления друг на друга двух натуральных чисел) и трансцендентное (то есть, не является результатом решения какого-нибудь степенного уравнения с рациональными коэффициентами). Для практического использования вполне достаточно запомнить две цифры после запятой: 2.71. Но существует мнемоническое правило, позволяющее запомнить 15 знаков после запятой в десятичном представлении числа e:
Два и семь, далее два раза год рождения Льва Толстого (1828), затем углы равнобедренного прямоугольного треугольника (45, 90 и 45 градусов).
Что такое число «е»?
Возникновение чисел в нашей жизни не случайность. Невозможно представить себе общение без использования чисел. Человечеству удалось установить целый ряд законов и закономерностей мира чисел, разгадать некоторые тайны и использовать свои открытия в повседневной жизни. Без замечательной науки о числах – математики – немыслимо сегодня ни прошлое, ни будущее. А сколько ещё не разгаданного! В незапамятные времена, научившись считать, люди познали меру количества – число. Вглядываясь в сочетания чисел, они с изумлением увидели, что числа имеют какую-то самостоятельную жизнь, удивительную и полную тайны; тайны необъяснимой и поэтому загадочной и многозначительной. Священные, волшебные, загадочные, таинственные, совершенные.… Как только их не называли!
В своей жизни каждый из нас стакивается с числами. Курс школьной программы, да и дальнейшую жизнь, трудно представить без них. Число е – это основание натуральных логарифмов и важнейшая математическая константа (обозначается строчной латинской буквой «e»), которая в высшей математике встречается буквально на каждом шагу, она играет особенно важную роль в дифференциальном и интегральном исчислении. Иногда число e называют числом Эйлера. Леонард Эйлер (1707 – 1783 гг.) – гениальный математик. Именно Эйлер первым ввел символ е (с этой буквы начинается его фамилия – Euler) и сделал так много открытий, связанных с этим числом, что, в конце концов, его стали называть числом Эйлера.
Число е – трансцендентное число (доказал Ш. Эрмит в 1873 г.), то есть оно не является корнем никакого многочлена с целыми коэффициентами, и не существует закона, по которому чередуются цифры после запятой в значении числа. Так что число е – это не случайное, взятое наугад число. Оно воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя.
Число е — это нечто вроде предела скорости (как «число с« — скорость света в вакууме). Эта константа показывает, как быстро можно вырасти, используя непрерывный процесс. Вы можете не всегда достигать предела скорости, но это удобная точка сравнения: вы можете описать любой коэффициент роста с помощью этой универсальной константы.
Число Пи — это соотношение длины окружности к диаметру, одинаковое для всех окружностей. Это фундаментальная пропорция, свойственная всем окружностям, а следовательно, она участвует в вычислении длины окружности, площади, объема и площади поверхности для кругов, сфер, цилиндров и т.д. Пи показывает, что все окружности связаны, не говоря уже о тригонометрических функциях, выводимых из окружностей (синус, косинус, тангенс).
В рекламных проспектах банков их составители особо подчеркивают, сколько раз в год производится начисление прибыли. Непосвященному может показаться, что при достаточно частом начислении процентов (например, если производит пересчет миллион раз в год) за 25 лет вклад превратится в весьма ощутимую сумму. В действительности ничего подобного не произойдет. Через 25 лет вклад вырос бы до величины, равному 2,718 суммы вклада, этот предел и называется числом е.
Предположим, что в банке, выплачивающем простой процент, один рубль через какой-то промежуток времени удваивается. При непрерывном начислении прибыли рубль за то же время превратился бы в е рублей независимо от того, сколько простых процентов прибыли выплачивает в действительности банк. Из вышеизложенного следует вывод, что число е является базовым соотношением роста для всех непрерывно растущих процессов. Оно позволяет взять простой темп прироста (где разница видна только в конце года) и вычислить составляющие этого показателя, нормальный рост, при котором с каждой наносекундой (или даже быстрее) всё вырастает еще на немного.







 eponim2008
eponim2008
