числа фибоначчи что оно значит
Число Фибоначчи. Почему оно так популярно в природе?
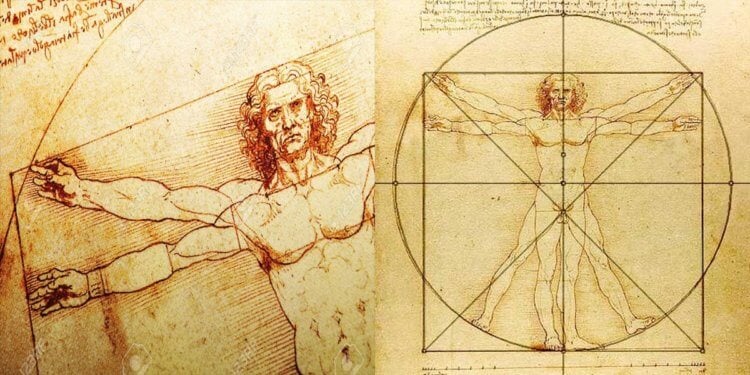
Таинственное число Фибоначчи, равное 1,618, будоражит умы ученых уже на протяжении нескольких тысячелетий. Кто-то считает это число строителем мироздания, кто-то называет его числом Бога, а кто-то, не мудрствуя лукаво, просто применяет его на практике и получает невероятные архитектурные, художественные и математические творения. Число Фибоначчи было обнаружено даже в пропорциях знаменитого «Витрувианского человека» Леонардо Да Винчи, который утверждал, что знаменитое число, пришедшее из математики, руководит всей Вселенной.
«Витрувианский человек» Леонардо да Винчи обладает идеальными пропорциями, основанными на знании свойств числа Фибоначчи
Кто такой Фибоначчи?
Леонардо Пизанский считается самым первым крупным математиком в истории средневековой Европы. Несмотря на это, свое знаменитое прозвище «Фибоначчи» ученый получил далеко не из-за своих экстраординарных математических способностей, но из-за своего везения, так как «боначчи» по-итальянски означает «удачливый». Перед тем как стать одним из самых известных математиков раннего Средневековья, Леонардо Пизанский изучал точные науки у самых продвинутых учителей своего времени, которыми считались арабы. Именно благодаря этой деятельности Фибоначчи, в Европе появились десятичная система счисления и арабские цифры, которыми мы пользуемся до сих пор.
В одном из своих самых известных трудов под названием «Liber abaci», Леонардо Пизанский приводит уникальную закономерность чисел, которые при постановке в ряд образуют линию цифр, каждая из которых является суммой двух предыдущих чисел.
Последовательность Фибоначчи
Иными словами, последовательность Фибоначчи выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 и так далее.
Каждое число из ряда Фибоначчи, разделенное на последующее, имеет значение, стремящееся к уникальному показателю, которое составляет 1,618. Первые числа ряда Фибоначчи не дают настолько точное значение, однако по мере нарастания, соотношение постепенно выравнивается и становится все более точным.
Леонардо Пизанский — тот самый создатель числа Фибоначчи
Где используется число Фибоначчи
Из-за своего повсеместного применения в природе, золотое сечение (именно так число Фибоначчи иногда называют в искусстве и математике) считается одним из самых гармонизирующих законов мироздания, который упорядочивает структуру окружающего нас мира и направляет жизнь на развитие. Так, правило золотого сечения применяется природой для образования траекторий движения вихревых потоков в ураганах, при образовании эллиптических галактик, к которым относится и наш Млечный Путь, при «строительстве» раковины улитки или ушной раковины человека, направляет движение косяка рыб и показывает траекторию движения испуганной стаи оленей, врассыпную убегающую от хищника.
Проявление золотого сечения в природе
Эстетичность такой гармонизации мироздания воспринимается человеком, который всегда стремился улучшить окружающую его действительность, в качестве стабилизирующего природу закона. Находя золотое сечение в лице того или иного человека, мы инстинктивно воспринимаем собеседника в качестве гармоничной личности, чье развитие происходит без сбоев и нарушений. Этим можно объяснить то, почему иногда нам по непонятным причинам больше нравится одно лицо, чем другое. Оказывается, о наших возможных симпатиях позаботилась природа!
Как вы считаете, является ли повсеместное применение числа Фибоначчи в природе совпадением или свидетельством наличия некоего вселенского разума? Давайте попробуем обсудить этот вопрос в нашем Telegram-чате.
Наиболее распространенное определение золотого сечения гласит, что меньшая часть так относится к большей, как большая часть относится ко всему целому. Уникальное правило встречается во всех областях природы, науки и искусства, позволив некоторым именитым исследователям Средних Веков сделать предположение, что три основные части золотого сечения олицетворяют собой христианских Отца, Сына и Святого Духа.
Правилу золотого сечения следуют даже галактики. Наш Млечный Путь в этом плане не является исключением
Что такое золотое сечение
С точки зрения математики, золотое сечение представляет собой некую идеальную пропорцию, к которой каким-то образом стремится все живое и неживое в природе.
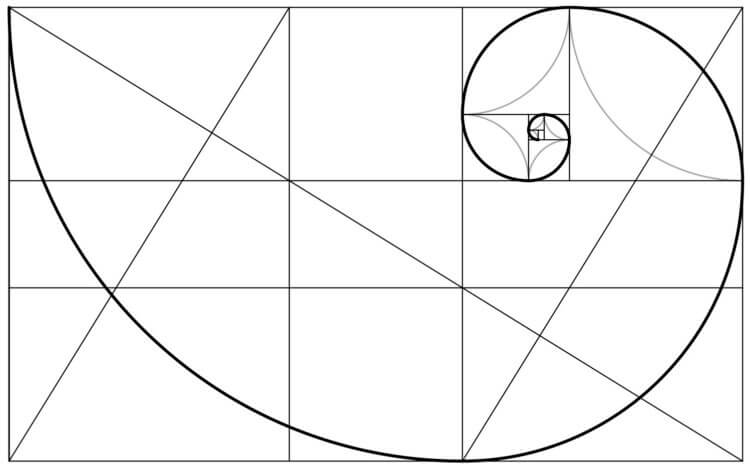
Так выглядит «золотое сечение»
Используя основные принципы ряда Фибоначчи, растут семечки в центре подсолнуха, движется спираль ДНК, был построен Парфенон и написана самая знаменитая картина в мире — «Джоконда» Леонардо Да Винчи.
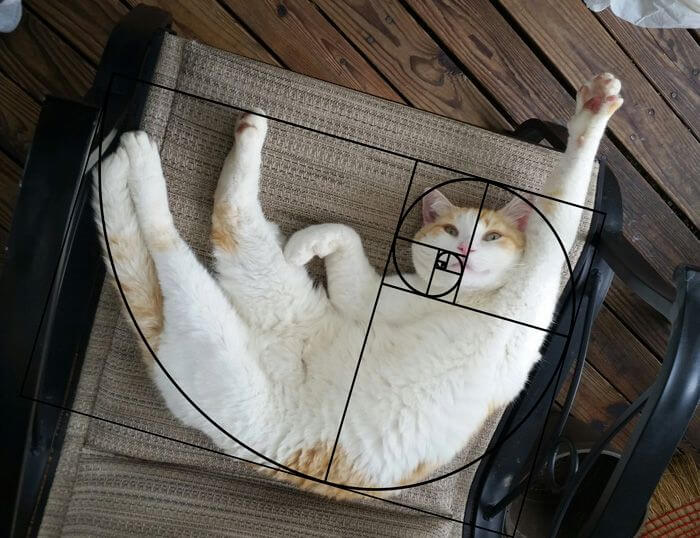
Даже коты неосознанно (хотя, кто знает?) следуют принципу золотого сечения, становясь любимцами большей части населения планеты
Есть ли в природе гармония? Несомненно, есть. А ее доказательством служит число Фибоначчи, происхождение которого нам еще только предстоит отыскать.
Новости, статьи и анонсы публикаций
Свободное общение и обсуждение материалов
Ни для кого из нас не секрет, что в космосе постоянно происходят разные события. Недавно ученые обнаружили самый яркий свет во Вселенной, который появился в …
Как бы вы не любили путешествия, на нашей планете есть места, куда вас не пустят ни за какие деньги. 💸 Большинство из этих мест опасны, потому что там вы можете заразиться опасными болезнями или стать жертвой аборигенов. Но есть и места, где проводятся таинственные ритуалы.
Кажется, что все что мы знаем о Вселенной, может быть в корне неверным. Так, согласно новому исследованию, наше мироздание может иметь форму гигантской петли…
Числа фибоначчи что оно значит
ВЫСШЕЕ НАЗНАЧЕНИЕ МАТЕМАТИКИ СОСТОИТ В ТОМ, ЧТОБЫ НАХОДИТЬ СКРЫТЫЙ ПОРЯДОК В ХАОСЕ, КОТОРЫЙ НАС ОКРУЖАЕТ.
Человек всю жизнь стремится к знаниям, пытается изучить окружающий его мир. И в процессе наблюдений у него возникают вопросы, на которые требуется найти ответы. Ответы находятся, но появляются новые вопросы. В археологических находках, в следах цивилизации, отдаленных друг от друга во времени и в пространстве, встречается один и тот же элемент – узор в виде спирали. Некоторые считают его символом солнца и связывают с легендарной Атлантидой, но истинное его значение неизвестно. Что общего между формами галактики и атмосферного циклона, расположением листьев на стебле и семян в подсолнухе? Эти закономерности сводятся к так называемой «золотой» спирали, удивительной последовательности Фибоначчи, открытой великим итальянским математиком XIII века.
История возникновения чисел Фибоначчи
Впервые о том, что такое числа Фибоначчи, я услышал от учителя математики. Но, кроме того, каким образом складывается последовательность этих чисел, я не знал. Вот чем на самом деле знаменита эта последовательность, каким образом она влияет на человека, я и хочу вам рассказать. О Леонардо Фибоначчи известно немного. Нет даже точной даты его рождения. Известно, что он родился в 1170 году в семье купца, в городе Пизе в Италии. Отец Фибоначчи часто бывал в Алжире по торговым делам, и Леонардо изучал там математику у арабских учителей. Впоследствии он написал несколько математических трудов, наиболее известным из которых является «Книга об абаке», которая содержит почти все арифметические и алгебраические сведения того времени. 2
Числа Фибоначчи – это последовательность чисел, обладающая рядом свойств. Эту числовую последовательность Фибоначчи открыл случайно, когда пытался в 1202 году решить практическую задачу о кроликах. «Некто поместил пару кроликов в некоем месте, огороженном со всех сторон со всех сторон стеной, чтобы узнать, сколько пар кроликов родится в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения». При решении задачи он учел, что каждая пара кроликов порождает на протяжении жизни еще две пары, а затем погибает. Так появилась последовательность чисел: 1, 1, 2, 3, 5, 8, 13, 21, … В этой последовательности каждое следующее число равно сумме двух предыдущих. Её назвали последовательностью Фибоначчи. Математические свойства последовательности
Мне захотелось исследовать эту последовательность, и я выявил некоторые её свойства. Эта закономерность имеет большое значение. Последовательность все медленнее приближается к некоему постоянному отношению, равному примерно 1, 618, а отношение любого числа к последующему примерно равно 0, 618.
размером 8х8 (всего 64 маленьких квадратика) на четыре части, длины сторон которых равны числам Фибоначчи. Теперь из этих частей построим прямоугольник размером 5х13. Его площадь составляют 65 маленьких квадратиков. Откуда же берется дополнительный квадрат? Все дело в том, что идеальный прямоугольник не образуется, а остаются крошечные зазоры, которые в сумме и дают эту дополнительную единицу площади. Треугольник Паскаля также имеет связь с последовательностью Фибоначчи. Надо только написать строки треугольника Паскаля одну под другой, а затем складывать элементы по диагонали. Получится последовательность Фибоначчи.
Теперь рассмотрим «золотой» прямоугольник, одна сторона которого в 1,618 раз длиннее другой. На первый взгляд он может показаться нам обычным прямоугольником. Тем не менее, давайте проделаем простой эксперимент с двумя обыкновенными банковскими картами. Положим одну из них горизонтально, а другую вертикально так, чтобы их нижние стороны находились на одной линии. Если в горизонтальной карте провести диагональную линию и продлить ее, то увидим, что она пройдет в точности через правый верхний угол вертикальной карты – приятная неожиданность. Может быть, это случайность, а может, такие прямоугольники и другие геометрические формы, использующие «золотое сечение», особенно приятны глазу. Думал ли Леонардо да Винчи о золотом сечении, работая над своим шедевром? Это кажется маловероятным. Однако можно утверждать, что он придавал большое значение связи между эстетикой и математикой.
Числа Фибоначчи в природе
Связь золотого сечения с красотой – вопрос не только человеческого восприятия. Похоже, сама природа выделила Ф особую роль. Если в «золотой» прямоугольник последовательно вписать квадраты, затем в каждом квадрате провести дугу, то получится элегантная кривая, которая называется логарифмической спиралью. Она вовсе не является математическим курьезом. 5
Природа даёт нам многочисленные примеры расположения однородных предметов, описываемых числами Фибоначчи. В разнообразных спиралевидных расположениях мелких частей растений обычно можно усмотреть два семейства спиралей. В одном из этих семейств спирали завиваются по часовой стрелке, а в другом – против. Числа спиралей одного и другого типов часто оказываются соседними числами Фибоначчи. Так, взяв молодую сосновую веточку, легко заметить, что хвоинки образуют две спирали, идущие слева снизу вправо вверх. На многих шишках семена расположены в трёх спиралях, полого навивающихся на стержень шишки. Они же расположены в пяти спиралях, круто навивающихся в противоположном направлении. В крупных шишках удаётся наблюдать 5 и 8, и даже 8 и 13 спиралей. Хорошо заметны спирали Фибоначчи и на ананасе: обычно их бывает 8 и 13.
Отросток цикория делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок ещё меньшего размера и снова выброс. Импульсы его роста постепенно уменьшаются в пропорции «золотого» сечения. Чтобы оценить огромную роль чисел Фибоначчи, достаточно лишь взглянуть на красоту окружающей нас природы. Числа Фибоначчи можно найти в количестве
ответвлений на стебле каждого растущего растения и в числе лепестков.
Пересчитаем лепестки некоторых цветов —ириса с его 3 лепестками, примулы с 5 лепестками, амброзии с 13 лепестками, нивяника с 34 лепестками, астры с 55 лепестками и т.д. Случайно ли это, или это закон природы? Посмотрите на стебли и цветы тысячелистника. Таким образом, суммарной последовательностью Фибоначчи можно легко трактовать закономерность проявлений «Золотых» чисел, встречаемых в природе. Эти законы действуют независимо от нашего сознания и желания принимать их или нет. Закономерности «золотой» симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов, в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.
Числа Фибоначчи в архитектуре
«Золотое сечение» проявляется и во многих замечательных архитектурных творениях на протяжении всей истории человечества. Оказывается, еще древнегреческие и древнеегипетские математики знали эти коэффициенты задолго до Фибоначчи и называли их «золотым сечением». Принцип «золотого сечения» греки использовали при строительстве Парфенона, египтяне – Великой пирамиды в Гизе. Достижения в области строительной техники и разработки новых материалов открыли новые возможности для архитекторов ХХ века. Американец Фрэнк Ллойд Райт был одним из главных сторонников органической архитектуры. Незадолго до смерти он спроектировал музей Соломона Гуггенхайма в Нью-Йорке, представляющий собой опрокинутую спираль, а интерьер музея напоминает раковину наутилуса. Польско-израильский архитектор Цви Хекер также использовал спиральные конструкции в проекте школы имени Хайнца Галински в Берлине, построенной в 1995 году. Хекер начал с идеи подсолнечника с центральным кругом, откуда
расходятся все архитектурные элементы. Здание представляет собой сочетание
ортогональных и концентрических спиралей, символизируя взаимодействие ограниченных человеческих знаний и управляемого хаоса природы. Его архитектура имитирует растение, которое следует за движением Солнца, поэтому классные комнаты освещены в течение всего дня.
В Куинси-парке, расположенном в Кембридже, штат Массачусетс (США), «золотую» спираль можно встретить часто. Парк был спроектирован в 1997 году художником Дэвидом Филлипсом и находится недалеко от Математического института Клэя. Это заведение является известным центром математических исследований. В Куинси-парке можно прогуливаться среди «золотых» спиралей и металлических кривых, рельефов из двух раковин и скалы с символом квадратного корня. На табличке написана информация о «золотой» пропорции. Даже парковка для велосипедов использует символ Ф.
Числа Фибоначчи в психологии
В психологии отмечены переломные моменты, кризисы, перевороты, знаменующие на жизненном пути человека преобразования структуры и функций души. Если человек успешно преодолел эти кризисы, то становится способным решать задачи нового класса, о которых раньше даже не задумывался.
Наличие коренных изменений дает основание рассматривать время жизни в качестве решающего фактора развития духовных качеств. Ведь природа отмеряет нам время не щедро, «ни сколько будет, столько и будет», а ровно столько, чтобы процесс развития материализовался:
в чувствах, мышлении и психомоторике — пока они не приобретут гармонию, необходимую для возникновения и запуска механизма
в структуре энергопотенциала человека.
Развитие тела нельзя остановить: ребенок становится взрослым человеком. С механизмом же творчества не так все просто. Его развитие можно остановить и изменить его направление.
Существует ли шанс догнать время? Безусловно. Но для этого нужно выполнить огромную работу над собой. То, что развивается свободно, естественным путем, не требует специальных усилий: ребенок свободно развивается и не замечает этой огромной работы, потому что процесс свободного развития создается без насилия над собой.
Как понимается смысл жизненного пути в обыденном сознании? Обыватель видит его так: у подножия — рождение, на вершине — расцвет сил, а потом — все идет под горку.
Мудрец же скажет: все намного сложнее. Восхождение он разделяет на этапы: детство, отрочество, юность… Почему так? Мало, кто способен ответить, хотя каждый уверен, что это замкнутые, целостные этапы жизни.
Чтобы выяснить, как развивается механизм творчества, В.В. Клименко воспользовался математикой, а именно законами чисел Фибоначчи и пропорцией «золотого сечения» — законами природы и жизни человека.
Числа Фибоначчи делят нашу жизнь на этапы по количеству прожитых лет: 0 — начало отсчета — ребенок родился. У него еще отсутствуют не только психомоторика, мышление, чувства, воображение, но и оперативный энергопотенциал. Он — начало новой жизни, новой гармонии;
1 — ребенок овладел ходьбой и осваивает ближайшее окружение;
2 — понимает речь и действует, пользуясь словесными указаниями;
3 — действует посредством слова, задает вопросы;
5 — «возраст грации» — гармония психомоторики, памяти, воображения и чувств, которые уже позволяют ребенку охватить мир во всей его целостности;
8 — на передний план выходят чувства. Им служит воображение, а мышление силами своей критичности направлено на поддержку внутренней и внешней гармонии жизни;
13 — начинает работать механизм таланта, направленный на превращение приобретенного в процессе наследования материала, развивая свой собственный талант;
21 — механизм творчества приблизился к состоянию гармонии и делаются попытки выполнять талантливую работу;
34— гармония мышления, чувств, воображения и психомоторики: рождается способность к гениальной работе;
55 — в этом возрасте, при условии сохраненной гармонии души и тела, человек готов стать творцом. И так далее…
Что же такое засечки «Чисел Фибоначчи»? Они могут быть сравнимы с плотинами на жизненном пути. Эти плотины ожидают каждого из нас. Прежде всего необходимо преодолеть каждую их них, а потом терпеливо поднимать свой уровень развития, пока в один прекрасный день она не развалится, открывая свободному течению путь к следующей.
Теперь, когда нам понятен смысл этих узловых точек возрастного развития, попробуем расшифровать, как все это происходит.
В1 год ребенок овладевает ходьбой. До этого он познавал мир передней частью головы. Теперь же он познает мир руками — исключительная привилегия человека. Животное передвигается в пространстве, а он, познавая, овладевает пространством и осваивает территорию, на которой живет.
2 года — понимает слово и действует в соответствии с ним. Это значит, что:
ребенок усваивает минимальное количество слов — смыслов и образов действий;
пока что не отделяет себя от окружающей среды и слит в целостность с окружающим,
поэтому действует по чужому указанию. В этом возрасте он самый послушный и приятный для родителей. Из человека чувственного ребенок превращается в человека познающего.
3 года— действие при помощи собственного слова. Уже произошло отделение этого человека от окружающей среды — и он учится быть самостоятельно действующей личностью. Отсюда он:
сознательно противостоит среде и родителям, воспитателям в детском саду и т.д.;
осознает свой суверенитет и борется за самостоятельность;
старается подчинить своей воле близких и хорошо знакомых людей.
Теперь для ребенка слово — это действие. С этого начинается действующий человек.
5 лет— «возраст грации». Он — олицетворение гармонии. Игры, танцы, ловкие движения — все насыщено гармонией, которой человек старается овладеть собственными силами. Гармоничная психомоторика содействует приведению к новому состоянию. Поэтому ребенок направлен на психомоторную активность и стремится к максимально активным действиям.
Материализация продуктов работы чувствительности осуществляется посредством:
способности к отображению окружающей среды и себя как части этого мира (мы слышим, видим, прикасаемся, нюхаем и т.д. — все органы чувств работают на этот процесс);
способности к проектированию внешнего мира, в том числе и себя
(создание второй природы, гипотез — сделать завтра то и другое, построить новую машину, решить проблему), силами критичности мышления, чувств и воображения;
способности к созиданию второй, рукотворной природы, продуктов деятельности (реализация задуманного, конкретные умственные или психомоторные действия с конкретными предметами и процессами).
После 5 лет механизм воображения выходит вперед и начинает доминировать над остальными. Ребенок выполняет гигантскую работу, создавая фантастические образы, и живет в мире сказок и мифов. Гипертрофированность воображения ребенка вызывает у взрослых удивление, потому что воображение никак не соответствует действительности.
8 лет — на передний план выходят чувства и возникают собственные мерки чувств (познавательных, нравственных, эстетических), когда ребенок безошибочно:
оценивает известное и неизвестное;
отличает моральное от аморального, нравственное от безнравственного;
прекрасное от того, что угрожает жизни, гармонию от хаоса.
13 лет — начинает работать механизм творчества. Но это не значит, что он работает на полную мощность. На первый план выходит один из элементов механизма, а все остальные содействуют его работе. Если и в этом возрастном периоде развития сохраняется гармония, которая почти все время перестраивает свою структуру, то отрок безболезненно доберется до следующей плотины, незаметно для себя преодолеет ее и будет жить в возрасте революционера. В возрасте революционера отрок должен сделать новый шаг вперед: отделиться от ближайшего социума и жить в нем гармоничной жизнью и деятельностью. Не каждый может решить эту задачу, возникающую перед каждым из нас.
21 год. Если революционер успешно преодолел первую гармоничную вершину жизни, то его механизм таланта способен выполнять талантливую
работу. Чувства (познавательные, моральные или эстетические) иногда затмевают мышление, но в общем все элементы работают слаженно: чувства открыты миру, а логическое мышление способно с этой вершины называть и находить меры вещей.
Механизм творчества, развиваясь нормально, достигает состояния, позволяющего получать определенные плоды. Он начинает работать. В этом возрасте вперед выходит механизм чувств. По мере того, как воображение и его продукты оцениваются чувствами и мышлением, между ними возникает антагонизм. Побеждают чувства. Эта способность постепенно набирает мощность, и отрок начинает ею пользоваться.
34 года— уравновешенность и гармоничность, продуктивная действенность таланта. Гармония мышления, чувств и воображения, психомоторики, которая пополняется оптимальным энергопотенциалом, и механизм в целом — рождается возможность исполнять гениальную работу.
55 лет — человек может стать творцом. Третья гармоничная вершина жизни: мышление подчиняет себе силу чувств.
Числа Фибоначчи называют этапы развития человека. Пройдет ли человек этот путь без остановок, зависит от родителей и учителей, образовательной системы, а дальше — от него самого и от того, как человек будет познавать и преодолевать самого себя.
На жизненном пути человек открывает 7 предметов отношений:
От дня рождения до 2-х лет — открытие физического и предметного мира ближайшего окружения.
От 2-х до 3-х лет — открытие себя: «Я — Сам».
От 3-х до 5-ти лет — речь, действенный мир слов, гармонии и системы «Я — Ты».
От 5-ти до 8-ми лет — открытие мира чужих мыслей, чувств и образов — системы «Я — Мы».
От 8 до 13 лет — открытие мира задач и проблем, решенных гениями и талантами человечества — системы «Я — Духовность».
От 13 до 21 года — открытие способностей самостоятельно решать всем известные задачи, когда мысли, чувства и воображение начинают активно работать, возникает система «Я — Ноосфера».
От 21 до 34 лет — открытие способности создавать новый мир или его фрагменты — осознание самоконцепции «Я — Творец».
Жизненный путь имеет пространственно-временную структуру. Он состоит из возрастных и индивидуальных фаз, определяемых по многим параметрам жизни. Человек овладевает в определенной мере обстоятельствами своей жизни, становится творцом своей истории и творцом истории общества. Подлинно творческое отношение к жизни, однако, появляется далеко не сразу и даже не у всякого человека. Между фазами жизненного пути существуют генетические связи, и это обусловливает закономерный его характер. Отсюда следует, что в принципе можно предсказывать будущее развитие на основе знания о ранних его фазах.
Числа Фибоначчи в астрономии
Из истории астрономии известно, что И.Тициус, немецкий астроном XVIII в., с помощью ряда Фибоначчи нашёл закономерность и порядок в расстояниях между планетами солнечной системы. Но один случай, казалось бы, противоречил закону: между Марсом и Юпитером не было планеты. Но после смерти Тициуса в начале XIX в. сосредоточенное наблюдение за этим участком неба привело к открытию пояса астероидов.
Заключение
В процессе исследования я выяснил, что числа Фибоначчи нашли широкое применение в техническом анализе цен на бирже. Один из простейших способов применения чисел Фибоначчи на практике – определение отрезков времени, через которое произойдёт то или иное событие, например, изменение цены. Аналитик отсчитывает определённое количество фибоначчиевских дней или недель (13,21,34,55 и т.д.) от предыдущего сходного события и делает прогноз. Но в этом мне ещё слишком сложно разобраться. Хотя Фибоначчи и был величайшим математиком средних веков, единственные памятники Фибоначчи – это статуя напротив Пизанской башни и две улицы, которые носят его имя: одна – в Пизе, а другая – во Флоренции. И всё-таки, в связи со всем увиденным и прочитанным мною возникают вполне закономерные вопросы. Откуда взялись эти числа? Кто этот архитектор вселенной, попытавшийся сделать её идеальной? Что же будет дальше? Найдя ответ на один вопрос, получишь следующий. Разгадаешь его, получишь два новых. Разберёшься с ними, появятся ещё три. Решив и их, обзаведёшься пятью нерешёнными. Потом восьмью, тринадцатью и т.д. Не забывайте, что на двух руках по пять пальцев, два из которых состоят из двух фаланг, а восемь – из трёх.
Литература:
Волошинов А.В. «Математика и искусство», М., Просвещение, 1992г.
Воробьёв Н.Н. «Числа Фибоначчи», М., Наука, 1984г.
Стахов А.П. «Код да Винчи и ряд Фибоначчи», Питер формат, 2006 г.
Ф. Корвалан «Золотое сечение. Математический язык красоты», М., Де Агостини, 2014 г.
Максименко С.Д. «Сенситивные периоды жизни и их коды».