числа близнецы в математике что это

Неизвестный математик совершил прорыв в теории простых чисел-близнецов

В математике чрезвычайно редко случается, чтобы учёный старше 40 лет опубликовал первую серьёзную научную работу. Ещё реже бывает, чтобы эта работа имела большую научную ценность. Именно такой редчайший случай представляет из себя доцент университета Нью-Гэмпшира Итан Чжан (Yitang Zhang), который до сих не имеет ни должности профессора, ни веб-странички со списком научных работ. Тем не менее, ему удалось совершить серьёзный шаг к решению одной из старейших математических проблем — гипотезе о простых числах-близнецах.

Когда журнал “Annals of Mathematics” получил 17 апреля 2013 года научную работу Чжана, они восприняли её скептически. Заявка на прорывное исследование от неизвестного учёного? Это слишком банально и часто встречается, чтобы оказаться правдой. На удивление редколлегии, несколько научных экспертов подробно изучили работу Чжана — и нашли доказательство гипотезы о расстоянии между парными простыми числами предельно ясным, чётким и бесспорным.

В результате, журнал одобрил работу для публикации в исключительно короткие сроки — уже через три недели после поступления.

В свои 50+ лет Итан Чжан преподаёт алгебраическую геометрию в университете, но теория чисел была его хобби. Как обычно, математики часто увлекаются простыми числами как одной из самых интересных загадок в этой области науки. Внимание Чжана привлекла теорема простых чисел-близнецов.

Решето Эратосфена — простой алгоритм нахождения всех простых чисел до некоторого целого числа n, путём вычёркивания всех чисел которые делятся на простой делитель: 2, 3, 5, 7 и т.д.

Математики давно обратили внимание, что распределение простых чисел в бесконечном числовом пространстве имеет определённые закономерности. В частности, странным феноменом выступают простые числа-близнецы, которые отличаются друг от друга на 2. Чем больше количество знаков, тем реже встречаются числа-близнецы, но всё равно они продолжают встречаться снова и снова.

В оригинальной версии гипотеза гласит, что существует бесконечное количество простых чисел-близнецов. Это предположение до сих пор никто не доказал и не опроверг. Самыми большими найденными простыми числами-близнецами, известными науке, являются 3756801695685 × 2 666669 – 1 и 3756801695685 × 2 666669 + 1.

Итан Чжан доказал, что существует бесконечно большое количество простых чисел, расстояние между которыми не превышает 70 миллионов. Эти пары будут встречаться всё реже и реже, но не исчезнут никогда, несмотря на действие теоремы о среднем расстоянии между простыми числами в 2,3 × N, где N — количество разрядов.

Другими словами, среднее расстояние между числами будет приближаться к бесконечности, по мере роста количества разрядов, но при этом всегда будут встречаться простые числа, удалённые друг от друга не более чем на 70 млн, что просто удивительно.

«Эта работа изменит правила игры, — говорит Эндрю Грэнвилль (Andrew Granville), теоретик в области теории чисел из Монреальского университета. — Иногда после появления нового доказательства то, что раньше казалось трудно доказать, становится просто небольшим расширением. Теперь нам нужно изучить работу и понять, что к чему». Но по качеству доказательства нет никаких вопросов: «Он проработал каждую деталь, так что никто не поставит его работу под сомнение», — добавил Грэнвилль.

UPD. Сама статья Чжана не опубликована в открытом доступе, но удалось найти выдержки из его выступления в Герварде 13 мая 2013 года (спасибо, EvgeshaS).

Источник

Братишка, ты цел?

Математики вплотную подошли к доказательству гипотезы о числах-близнецах

Фотография: Eddy Van 3000 / flickr.com

Ряд простых чисел постепенно становится все более редким. Если взять отрезок фиксированной длинны и перемещать его вперед по числовой оси, он все реже будет «зацеплять» хотя бы одно простое число. На самом деле верно даже более сильное утверждение: для отрезка любой длины можно уехать так далеко, что в какой-то момент в него не попадет ни одного простого числа! То есть щели между простыми числами могут быть сколь угодно большими.

Но иногда соседние числа идут буквально друг за другом. С помощью современного компьютера мы можем найти практически любое количество простых чисел, но этого мало, для того, чтобы понять, как они ведут себя еще дальше, для того, чтобы сделать выводы о поведении их ряда в целом. Именно с распределением простых чисел связано множество интересных гипотез.

Одна из них — гипотеза о простых числах-близнецах: существует бесконечное количество простых чисел, отличающихся друг от друга на 2. Таких пар много в начале ряда: 3 и 5, 5 и 7, 11 и 13, 17 и 19, 29 и 31. Наибольшие известные на сегодняшний день простые близнецы, полученные с помощью компьютерных вычислений, это 3,756,801,695,685×2 666,669 — 1 и 3,756,801,695,685×2 666,669 + 1. Но будут ли простые близнецы встречаться сколь угодно далеко, до сих пор неизвестно.

На самом деле до недавнего времени не было ответа на более простой вопрос: верно ли, что расстояния между соседними простыми числами растут с ростом простых чисел? Используя аналогию с линейкой, верно ли, что для любой линейки, начиная с какого-то момента, она начнет зацеплять не больше одного простого числа за раз? Разумеется, если гипотеза о числах близнецах верна, то ответ на этот вопрос отрицательный.

Ответ (разумеется, отрицательный) на этот более простой вопрос впервые дал малоизвестный математик Итан Чжан из Университета Нью-Гэмпшира. Работа Чжана, опубликованная в мае 2013 года в научном журнале Annals of Mathematics оказалась полнейшей неожиданностью для математического сообщества. Чжану удалось сделать самый существенный прорыв в понимании поведения последовательных простых чисел за последние несколько сотен лет.

Чжан доказал, что существует бесконечное количество пар подряд идущих простых чисел, отстоящих друг от друга на 70 миллионов. 70 000 000 это еще не 2, что требовалось бы для доказательства гипотезы о простых близнецах, но уже и далеко не бесконечность.

70 000 000: Итан Чжан

В основе доказательства Чжана лежит специальный объект — так называемый подтверждающий гребень.

Назовем гребнем упорядоченное множество различных неотрицательных целых чисел ₁. h_k>. Его можно представлять себе как расческу шириной в h_k зубьев, у которой выломаны все зубья, кроме тех, которые стоят на позициях с номерами h_i. Мы хотим двигать гребень по натуральному ряду и смотреть, попадают ли одновременно все его зубья на простые числа, другими словами, являются ли для данного n все числа вида n+h₁. n+h_k простыми.

Возьмем простейший пример, гребень вида <0, 1>. В таком гребне k = 2, h₁ = 0, h₂=1. Число 1 по определению не считается простым, так что гребень интересно примерять к натуральным числам начиная со второй позиции. Тогда его зубцы укажут на 2 и 3 — оба эти числа простые. Но очевидно, что если двигать расческу дальше, то один из ее зубцов будет обязательно указывать на четное число большее 2-х, которое не является простым. Неинтересный случай.

А что, если взять гребень ? Ясно, что оба его зубца будут попадать на простые числа, пока будут находиться те самые пары простых близнецов. Из этих примеров можно сделать два вывода. Во-первых, изучение свойств «гребней» тесно связано с исходной задачей (точнее, они эквивалентны). Во-вторых, среди гребней есть такие, которые, как изначально неинтересны, потому что какой-то из их зубцов обязательно будет указывать на составное число. Можно ли заранее описать класс интересных гребней и дальше изучать именно их? Оказывается, — и это самое удивительное — да.

Давайте предположим, что наш гребень — не подтверждающий. Значит, для какого-то простого числа p остатки от деления h_i на p пробегают все значения от 0 до p-1. Продвинем гребень на любую позицию n>p. Его зубья указывают на числа n+h₁. n+h_k. Пусть остаток от деления n на p равен m. Так как гребень у нас не подтверждающий, среди в наборе зубцов есть один, скажем h_k, остаток от деления которого на p равен p-m. Тогда в сдвинутом на n-ю позицию гребне этот зубец укажет на число n+h_k, остаток которого при делении на p равен p-m+m = p. Значит, этот зубец указывает на число делящееся на p и строго большее его, это число — составное. Таким образом мы доказали, что хотя бы один зубец не подтверждающего гребня, сдвинутого на любую позицию n>p, приходится на составное число.

Фотография: Naomi Campbell / flickr.com

Источник

Простые близнецы

Простые числа-близнецы это пара простых чисел, отличающихся на 2.

Все пары простых-близнецов, кроме (3, 5) имеют вид .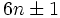

Первые простые числа-близнецы:

На данный момент, наибольшими известными простыми-близнецами являются числа 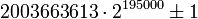[1].

Предполагается, что таких пар бесконечно много, но это не доказано. По гипотезе Харди-Литтлвуда, количество π₂(x) пар простых-близнецов, не превосходящих x, асимптотически приближается к

где C₂ — константа простых-близнецов:

Содержание

Теорема Бруна

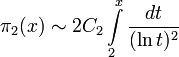
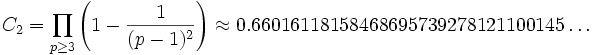
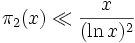Вигго Брун в 1919 доказал, что и ряд обратных величин сходится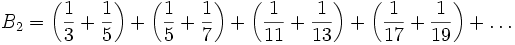

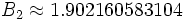Это означает, что если простых близнецов и бесконечно много, то они все же расположены в натуральном ряду довольно редко.

Значение называется константой Бруна для простых-близнецов.

Впоследствии была доказана сходимость аналогичного ряда для обобщенных простых близнецов.

Списки

Самые большие известные простые близнецы

Простые числа-триплеты

Первые простые числа-триплеты:

На данный момент, наибольшими известными простыми-триплетами являются числа:

(p, p+2, p+6), где p = 2072644824759 × 2 33333 − 1 (10047 цифр, ноябрь, 2008, Norman Luhn, François Morain, FastECPP)

См. также

Полезное

Смотреть что такое «Простые близнецы» в других словарях:

Простые числа-близнецы — Простые числа близнецы, или парные простые числа пары простых чисел, отличающихся на 2. Содержание 1 Общая информация 2 Теорема Бруна 3 Списки … Википедия

БЛИЗНЕЦЫ — простые близнецы, два простых числа с разностью, равной 2. Обобщенные близнецы пары соседних простых чисел с разностью 2т, где т фиксированное натуральное число. Пользуясь таблицей простых чисел, легко указать примеры Б. Это 3 и 5, 5 и 7, 11 и 13 … Математическая энциклопедия

Простые числа, отличающиеся на шесть — Простые числа, отличающиеся на шесть пара простых чисел вида «p, p + 6»[1]. Например, таковыми являются числа 5 и 11. В английском языке для таких пар чисел применяется термин «sexy primes» (англ. sexy сексуальный, возбуждающий,… … Википедия

Список простых чисел — Эта страница содержит список первых 500 простых чисел а также некоторые другие простые числа. Содержание 1 Первые 500 простых чисел 2 Простые числа Белла … Википедия

Чисел теория — наука о целых числах. Понятие целого числа (См. Число), а также арифметических операций над числами известно с древних времён и является одной из первых математических абстракций. Особое место среди целых чисел, т. е. чисел. 3 … Большая советская энциклопедия

БРУНА ТЕОРЕМА — о простых близнецах: ряд сходится, если рпробегает все простые близнецы. Это означает, что если простых близнецов и бесконечно много, то они все же расположены в натуральном ряду довольно редко. Теорема доказана В. Вруном [1]. Впоследствии была… … Математическая энциклопедия

Нерешённые проблемы математики — Нерешённые проблемы (или Открытые проблемы) проблемы, которые рассматривались математиками, но до сих пор не решены. Часто принимают форму гипотез, которые предположительно верны, но нуждаются в доказательстве. В научном мире популярна практика… … Википедия

Нерешенные проблемы математики — Нерешённые проблемы (или Открытые проблемы) проблемы, которые рассматривались математиками, но до сих пор не решены. Часто принимают форму гипотез, которые предположительно верны, но нуждаются в доказательстве. В научном мире популярна практика… … Википедия

Нерешенные проблемы теории чисел — Нерешённые проблемы (или Открытые проблемы) проблемы, которые рассматривались математиками, но до сих пор не решены. Часто принимают форму гипотез, которые предположительно верны, но нуждаются в доказательстве. В научном мире популярна практика… … Википедия

Источник

Большие гипотезы о простых числах доказаны для небольших числовых систем

Гипотеза о простых числах-близнецах – один из самых важных и сложных вопросов математики. Двое математиков решили параллельную версию этой задачи для небольших числовых систем.

7 сентября два математика опубликовали доказательство варианта одной из известнейших открытых задач математики. Полученный результат открывает новый фронт в изучении гипотезы о простых числах-близнецах, терзающей математиков вот уже более ста лет, и связанной с некоторыми из глубочайших свойств арифметики.

«Мы давно уже буксовали и у нас заканчивались идеи по этой задаче, поэтому естественный восторг вызывает появление у кого-либо новых идей», — сказал Джеймс Майнард, математик из Оксфорда.

Гипотеза о простых числах-близнецах касается пар простых чисел, отличающихся на 2. Близнецами являются числа 5 и 7. И 17 и 19. Гипотеза утверждает, что таких пар среди натуральных чисел существует бесконечное множество. За последнее десятилетие математики добились существенного прогресса, но до полного решения задачи им ещё очень далеко.

Авторы нового доказательства, Уил Савин из Колумбийского университета и Марк Шустерман из Висконсинского университета в Мэдисоне, доказали гипотезу для менее крупного, но всё же заметного математического мира. Они доказали её справедливость в случае конечной числовой системы, в которой есть лишь несколько чисел.

Такие числовые системы называются «конечными полями». Несмотря на их малый размер, они сохраняют множество математических свойств, присущих бесчисленным целым числам. Математики пытаются искать ответы на вопросы арифметики в конечных полях, и надеются транслировать эти результаты на все целые числа.

«Конечная мечта, пусть и немного наивная, заключается в том, что хорошее понимание свойств конечного поля может пролить свет на мир целых чисел», — сказал Майнард.

Кроме доказательства гипотезы о простых числах-близнецах Савин и Шустерман нашли ещё более удивительный результат, касающийся поведения простых чисел в небольших числовых системах. Они доказали, с какой именно частотой простые числа-близнецы появляются на небольших интервалах – и этот результат даёт возможность чрезвычайно точно контролировать такое явление, как простые числа-близнецы. Математики мечтают достичь сходных результатов и с обычными числами; они исследуют новое доказательство в поисках идей, применимых к простым числам на числовой прямой.

Новый вид простых чисел

Самое известное предсказание гипотезы о простых числах-близнецах заключается в наличии бесконечно большого количества пар чисел, различающихся на 2. Однако это утверждение более общее. Оно говорит о том, что существует бесконечное количество простых чисел, различающихся на 4 (к примеру, 3 и 7), или на 14 (293 и 307), или на любое заданное вами число.

Альфонс де Полиньяк сделал это предположение в его современном виде в 1849 году. За последовавшие 160 лет математики не сильно продвинулись с ним. Однако в 2013 году лёд тронулся, или, по крайней мере, серьёзно треснул. В тот год Чжан Итан доказал наличие бесконечно большого количества пар простых чисел, отличающихся друг от друга не более, чем на 70 млн. В следующем году другие математики, включая Мэйнарда и Терри Тао, серьёзно уменьшили этот разрыв. Текущим рекордом служит доказательство существования бесконечно большого количества пар простых чисел, отличающихся друг от друга не более, чем на 246.

Однако после этого прогресс утих. Математики понимают необходимость совершенно новой идеи для полного решения данной задачи. И конечные числовые системы – неплохое место для поисков этой идеи.

Чтобы построить конечное поле, сначала нужно извлечь конечное подмножество чисел из натуральных. Можно, к примеру, взять первые пять чисел (или любое простое количество). И вместо того, чтобы, как обычно, представлять числа на числовой линии, представьте новую числовую систему в виде циферблата.

Арифметика, как вы могли догадаться, начинает работать в замкнутом пространстве. Чему будет равно 4 + 3 в конечной числовой системе, состоящей из пяти элементов? Начнём с 4, отсчитаем три деления по часовой стрелке, и придём к 2. Вычитание, умножение и деление работают сходным образом.

Но только тут есть подвох. На конечных полях не имеет смысла обычное определение простого числа. На конечном поле любое число делится на любое другое. К примеру, 7 обычно не делится на 3. Но на конечном поле из пяти элементов – делится. Всё потому, что на этом конечном поле число 7 эквивалентно числу 12 – они оба заканчиваются на отметке 2 циферблата. Поэтому 7 разделить на 3 даст то же самое, что и 12 разделить на 3 – а 12, делённое на 3, даст 4.

Поэтому гипотеза простых чисел-близнецов для конечных полей относится к простым многочленам – таким математическим выражениям, как, например, x 2 + 1.

Допустим, к примеру, что ваше конечное поле содержит числа 1, 2 и 3. Эти числа будут коэффициентами многочлена в этом конечном поле, а «простым» многочленом будет такой, который нельзя разложить на множители-многочлены. Поэтому x 2 + x + 2 будет простым, поскольку его нельзя разложить на множители, а x 2 — 1 не будет: это произведение (x + 1) и (x − 1).

Определив простые многочлены, естественно задать вопрос о простых многочленах-близнецах – парах многочленов, являющихся простыми, и отличающихся на фиксированное значение. К примеру, многочлен x 2 + x + 2 простой, как и x 2 + 2x + 2. Отличаются они на x.

Гипотеза о простых многочленах-близнецах для конечных полей говорит о существовании бесконечно большого количества пар простых многочленов-близнецов, отличающихся не просто на x, а на любое значение.

Аккуратные разрезы

Понятия конечных полей и простых многочленов могут показаться притянутыми за уши, и бесполезными для изучения свойств чисел. Но они похожи на симулятор урагана – вселенную в себе, дающую идеи по поводу явлений, происходящем в большом мире.

«Между целыми числами и многочленами существует древняя аналогия, позволяющая преобразовывать потенциально крайне сложные задачи, связанные с целыми числами, в задачи, связанные с многочленами, которые тоже потенциально сложны, но, возможно, легче поддаются решению», — сказал Шустерман.

Конечные поля приобрели известность в 1940, когда Андре Вейль, разработал точный способ трансляции арифметики небольших числовых систем в арифметику целых чисел. Вейль использовал эту связь с потрясающими результатами. Он доказал, возможно, самую важную проблему в математике – гипотезу Римана – для случая с набором кривых над конечными полями (эта задача известна под именем геометрической гипотезы Римана). Это доказательство, вместе с набором дополнительных гипотез Вейля сделало конечные поля богатым ландшафтом для математических открытий.

Ключевой идеей Вейля было то, что на конечных полях геометрические техники можно использовать для поиска ответов на вопросы по поводу чисел. «Это особенность конечных полей. Многие задачи, которые вы хотите решить, можно перефразировать геометрически», — сказал Шустерман.

Чтобы понять, как в таком окружении появляется геометрия, представьте себе каждый многочлен в виде точки в пространстве. Коэффициенты многочлена служат координатами, определяющими его местоположение. Возвращаясь к нашему конечному полю из 1, 2 и 3, многочлен 2x + 3 расположится в точке (2, 3) двумерного пространства.

Но даже в простейшем конечном пространстве есть бесконечное множество многочленов. Можно создавать более сложные многочлены, увеличивая показатель самой большой экспоненты, или степень выражения. В нашем случае многочлен x 2 − 3x − 1 будет представлен точкой в трёхмерном пространстве. А многочлен 3x 7 + 2x 6 + 2x 5 − 2x 4 − 3x 3 + x 2 − 2x + 3 будет представлен точкой в восьмимерном пространстве.

В новой работе это геометрическое пространство представляет все многочлены заданной степени для заданного конечного поля. Вопрос превращается в следующий: есть ли способ изолировать все точки, обозначающие простые многочлены?

Стратегия Савина и Шустермана заключается в том, чтобы разделить пространство на две части. В одной части будут все точки, соответствующие многочленам с чётным количеством множителей. В другой – все точки, соответствующие многочленам с нечётным количеством множителей.

Это уже упрощает задачу. Гипотеза простых многочленов-близнецов для конечных полей относится только к многочленам с одним множителем (точно так же, как у простого числа есть один множитель, оно само). И поскольку число 1 нечётное, часть пространства, содержащего многочлены с чётным числом множителей, можно сразу выбросить.

Трюк состоит в использовании деления. В случае с двумерным объектом, например, поверхностью сферы, его разрезает пополам одномерная кривая – так, как экватор разрезает поверхность Земли. Объект с большим числом измерений всегда можно разрезать объектом с числом измерений, меньшим на единицу.

Кривые, нарисованные функцией Мёбиуса, гнутся и извиваются, как бешеные, пересекаясь сами с собою во многих местах. Эти места, называемые сингулярностями, особенно тяжело проанализировать (они соответствуют многочленам, раскладываемым на несколько одинаковых простых множителей).

Принципиальной инновацией Савина и Шустермана было то, что они нашли точный способ разрезать петли с меньшим числом измерений на более короткие отрезки. Эти отрезки было легче изучать, чем петли целиком.

Составив каталог многочленов с нечётным количеством простых множителей – а это было самое трудное — Савин и Шустерман столкнулись с задачей определения того, какие из них простые, и какие – близнецы. Для этого они применили несколько формул, используемых математиками для изучения простых чисел среди обычных.

Савин и Шустерман использовали свою технику, чтобы доказать два важных момента касательно простых многочленов на определённых конечных полях.

Во-первых, гипотеза простых чисел-близнецов на конечных полях верна: существует бесконечно много пар простых многочленов-близнецов, отличающихся на любую заданную величину.

Во-вторых, что более важно, эта работа обеспечивает точный подсчёт количества простых многочленов-близнецов, которые можно найти среди многочленов определённого порядка. Это аналогично знанию о том, сколько простых чисел-близнецов есть внутри любого достаточно длинного интервала на числовой прямой – и это просто мечта математиков.

«Это первая работа, дающая количественную аналогию того, что должно быть истинным для целых чисел, и это реально выдающийся результат, — сказал Зив Рудник из Тель-Авивского университета. – До сих пор ничего подобного не было».

Доказательство Савина и Шустермана показывает, как, спустя почти 80 лет после того, как Андре Вейль доказал гипотезу Римана для кривых над конечными полями, математики всё ещё с упорством движутся в эту сторону. Теперь математики, разбирающиеся с гипотезой простых чисел-близнецов, обратятся к работе Савина и Шустермана, и, возможно, она даст им глубокий источник вдохновения.

Источник

• ← во сне месила тесто руками к чему снится женщине
• Я много чего умею →