было 4 шара стало 6 шаров что произошло
Примеры моделей для решения задач
| Задача | Модель | Интерпретация модели |
| 1. Было 6 шаров, из них потеряно 4 шара. Сколько шаров осталось? | © н—о | Известно: начальное состояние объекта; направленность отношения между начальным и конечным состояниями объекта; числовое значение величины отношения между состояниями объекта. Определить: числовое значение величины конечного состояния объекта |
| 2. Было 4 шара, стало 6 шаров. Что произошло? | 171 »Гё1 | Известно: начальное состояние объекта; направленность отношения между ними. Определить: характер и числовое значение величины отношений между состояниями объекта. |
| 3. Имеется 6 шаров после того, как выиграно 4 шара. Сколько шаров было до выигрыша? | © п—-и | Известно: значение величины конечного состояния объекта, направленность отношений между состояниями объекта и числовое значение величины отношений между состояниями объекта. Определить: числовое значение величины начального состояния объекта |
| 4. Было 6 шаров, стало 4 шара. Что произошло? | н—-и | Известно: значение величины начального и конечного состояний объекта, направленность отношений между состояниями объекта. Определить: числовое значение величины отношения между состояниями объекта. |
01 J
| 5. В первой партии было выиграно 6 шаров, во второй партии было проиграно 4 шара. Что произошло в результате игры? | ®® О | Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта (начального, промежуточного и конечного). Определить: значение величины отношения между начальным и конечным состояниями объекта |
| 6. В первой партии было проиграно 6 шаров, во второй партии выиграно 4 шара. Что произошло в результате игры? | ® © —► —► | Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта. Определить: значение величины отношения между начальным и конечным состояниями объекта |
| 7. В первой партии было проиграно 4 шара. После того как была сыграна вторая партия, всего было потеряно 6 шаров. Что произошло во второй партии? | © О © | Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта. Определить: значение величины отношения между начальным и конечным состояниями объекта |
| 8. В первой партии было проиграно 6 шаров. После того как была сыграна вторая партия, всего было потеряно 4 шара. Что произошло во второй партии? | © О © | Известно: направленность отношений между состояниями объекта; значение величин отношений между начальным и промежуточным, между промежуточным и конечным состояниями объекта. Определить: отношения между промежуточным и конечным состояниями объекта |
Необходимо обратить внимание на то, что при построении моделей к задачам 5—8 значение величины начального
объекта не указывается ни в тексте задачи, ни на модели: оно не является искомым и его конкретная величина не имеет значения для решения задачи. Смысл анализа и решения этих задач заключается в определении характера и количественного выражения отношений между состояниями объекта («выигрыш — проигрыш»).
Таким образом, в моделях, создаваемых для анализа текста и решения задач Ж. Верньё, отображается прежде всего структура задачи, в которой фиксируются состояния объекта, характер и величина отношений между состояниями. Такого рода модели позволяют материализовать схему анализа содержания задачи, ее математический смысл, установить на основе структуры, что является известным, а что необходимо определить, и выстроить последовательность действий для решения задачи.
Использование тех же самых знаково-символических средств (окружность, вектор и др.) может не только приводить к созданию моделей, представляющих структурные компоненты задачи и их отношения, но и наглядно фиксировать последовательность действий в решении задачи. Это отличает их от описанных выше моделей Ж. Верньё, где действия и их последовательность выводятся из схемы отношений. Создание и фиксирование моделей достигается тем, что в язык символов вводятся специальные знаки известных и неизвестных компонентов задачи. Так, известные компоненты обозначаются сплошной линией, а неизвестные — пунктирной.
Один из таких наборов символов может быть представлен в следующем виде:
О— объект;
( )— искомое значение величины объекта;
а, в — значения величин объекта;
—>-— дано значение величины объекта;
—*-— не дано или задано опосредованно значение величины объекта;
/\— вид арифметического действия:
/1\— сложение;
/2\— вычитание;
/3\— умножение;
4\ — деление.
В зависимости от отношений между величинами объектов модели могут иметь разный вид.
03 \
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Текстовые задачи Моделирование и его роль в решении задач (стр. 3 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 |
Таким образом, в моделях Ж. Верньё, создаваемых для анализа текста и решения задач, отображается прежде всего структура задачи, в которой фиксируются состояния объекта, преобразование (трансформация) объекта, характер и величина отношений между состояниями. Такого рода модели позволяют материализовать схему анализа содержания задачи, её математический смысл, установить на основе структуры, что является известным, а что необходимо определить, и выстроить последовательность действий для решения задачи.
Использование знаково – символических средств (круг, квадрат, стрелка и др.) может приводить к созданию моделей, представляющих не только структурные компоненты задачи и их отношения, но и наглядно фиксировать последовательность действий по решению задачи.
В зависимости от отношений между величинами объектов модели могут иметь разный вид.
Известно: начальное состояние объекта; направленность отношения между начальным и конечным состоянием объекта; числовое значение величины отношения между состояниями объекта.
Необходимо определить числовое значение величины конечного состояния объекта.
Известно: начальное и конечное состояние объекта; направленность отношения между ними.
Необходимо определить характер и числовое значение величины отношений между состояниями объектов.
Известно: значение величины конечного состояния объекта, направленность отношений между состояниями объекта и числовое значение величины отношений между состояниями объектов.
Необходимо определить числовое значение величины начального состояния объекта.
Известно: значение величины начального и конечного состояния объекта, направленность отношений между состояниями объекта.
Необходимо определить числовое значение величины отношения между состояниями объектов.
Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта (начального, промежуточного и конечного).
Необходимо определить значение величины отношения между начальным и конечным состояниями объекта.
Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта.
Необходимо определить значение величины отношения между начальным и конечным состояниями объекта.
Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта.
Необходимо определить значение величины отношения между начальным и конечным состояниями объекта.
Известно: направленность отношений между состояниями объекта; значение величин отношений между начальным и промежуточным, между промежуточным и конечным состоянием объекта.
Необходимо определить отношения между промежуточным и конечным состояниями объекта.
ебенок, математика и реальность. Проблемы преподавания математики в начальной школе. Пер. с франц. – М.; Институт психологии РАН, 1998. Теория развивающего обучения. – М.; 1996. Знак и символ в обучении. – М.; 1988 Математика для педагогических училищ. Уч. пос. – М.: ИД «Форум» ИНФРА – 2017г. ЭБС
Опорный конспект к теме: «ТЕКСТОВЫЕ ЗАДАЧИ»
Примеры моделей для решения задачи
| Задача | Модель | Интерпретация модели |
| 1 | 2 | 3 |
| 1.Было 6 шаров, из них потеряно 4 шара. Сколько шаров осталось? |  | Известно: начальное состояние объекта; направленность отношения между начальным и конечным состояниями объекта; числовое значение величины отношения между состояниями объекта. Определить: числовое значение величины конечного состояния объекта |
| 2. Было 4 шара, стало 6 шаров. Что произошло7 | 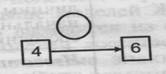 | Известно: начальное состояние объекта; направленность отношения между ними. Определить: характер и числовое значение величины отношений между состояниями объекта. |
| 3. Имеется 6 шаров после того, как выиграно 4 шара. Сколько шаров было до выигрыша? | 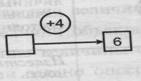 | Известно: значение величины конечного состояния объекта, направленность отношений между состояниями объекта и числовое значение величины отношений между состояниями объекта. Определить: числовое значение величины начального состояния объекта |
| 4.Было 6 шаров, стало 4 шара. Что произошло? |  | Известно: значение величины начального и конечного состояний объекта, направленность отношений между состояниями объекта. Определить: числовое значение величины отношения между состояниями объекта. |
| 5. В первой партии было выиграно 6 шаров, во второй партии было проиграно 4 шара. Что произошло в результате игры? | 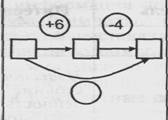 | Известно: направленное отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта (начального, промежуточного и конечного). Определить: значение личины отношения между начальным и конечным состояниями объекта |
| 6. В первое партии было проиграно 6 шаров. Во второй 4 шара. Что произошло в результате игры? |  | Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта. Определить: значение величины отношения между начальным и конечным состояниями объекта |
| 7. В первой партии было проиграно 4 шара. После того как была сыграна вторая партия, всего было потеряно 6 шаров. Что произошло во второй партии | 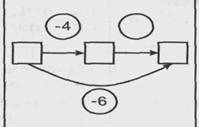 | Известно: направленно отношений между состояниями объекта; числовое значение величин отношений между состояниями, объекта. Определить: значение величины отношения между начальным и конечным состояниями объекта |
| 8. В перовой партии было проиграно 6 шаров. После того как была сыграна вторая партия, всего было потеряно 4 шара. Что произошло во второй партии? | 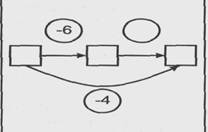 | Известно: направленность отношений между состояниями объекта; значение величин отношений между начальным и промежуточным, между промежуточным и конечным состояниями объекта. Определить: отношения между промежуточным и конечным состояниями объекта |
Необходимо обратить внимание на то, что при построении моделей к задачам 5-8 значение величины на имеет значения для решения задачи. Смысл анализа и решения этих задач заключается в определении характера и количественного выражения отношений между состояниями объекта («выигрыш — проигрыш»).
Таким образом, в моделях, создаваемых для анализа текста и решения задач Ж. Верньё, отображается прежде всего структура задачи, в которой фиксируются состояния объекта, характер и величина отношений между состояниями. Такого рода модели позволяют материализовать схему анализа содержания задачи, ее математический смысл, установить на основе структуры, что является известным, а что необходимо определить, и выстроить последовательность действий для решения задачи.
Использование тех же самых знаково-символических средств (окружность, вектор и др.) может не только приводить к созданию моделей, представляющих структурные компоненты задачи и их отношения, но и наглядно фиксировать последовательность действий в решении задачи. Это отличает их от описанных выше моделей Ж. Верньё, где действия и их последовательность выводятся из схемы отношений. Создание и фиксирование моделей достигается тем, что в язык символов вводятся специальные знаки известных и неизвестных компонентов задачи. Так, известные компоненты обозначаются сплошной линией, а неизвестные — пунктирной.
Один из таких наборов символов может быть представлен в следующем виде:
В зависимости от отношений между величинами объектов модели могут иметь разный вид.
Покажем это на примере так называемых косвенных, или инвертированных, задач, которые, как указывается в методической литературе, являются сложными для решения. Специфика таких задач состоит в том, что при их решении используется арифметическое действие, обратное тому, которое соответствует опорным словами текста задачи.
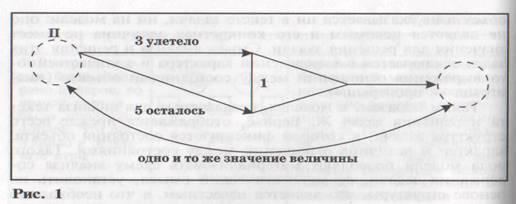
Типичной является задача: «На дереве сидели птички 3 птички улетели, осталось 5. Сколько птичек сидело на дереве?» Ошибкой многих учащихся начальной школы при решении таких задач является то, что они ориентируются на опорное слово «улетели» и поэтому используют вычитание (3 из 5), а не отношение между данными, которое привело бы их к правильному решению. Эти трудности могут быть снятья через построение моделей с использованием указанной выше* символики. Рассмотрим, например, модель на рисунке 1.
В данной задаче объект один — птички. Количество сидящих на дереве птиц (значение искомой величины) неизвестно. Оно представлено на модели двумя пунктирными окружностями: первая обозначает объект (искомое значения величины объекта), вторая — результат действия (тоже искомое значение величины объекта). Задача решается с помощью действия сложения, которое выбирается на основе восстановления сюжетной ситуации, описанной в тексте.
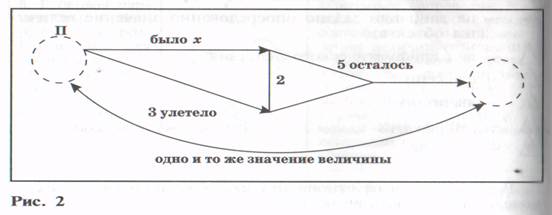
Эта задача может иметь такую модель (см. рис. 2).
В соответствии с этой моделью неизвестное будет находиться путем решения уравнения х — 3 = 5.
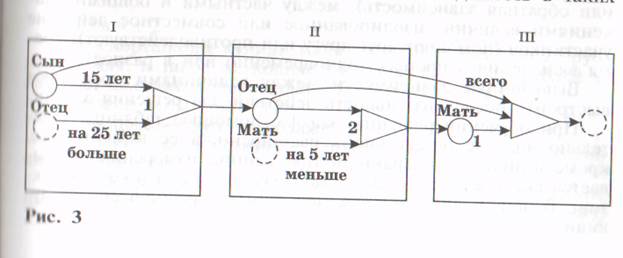
Выявление последовательности действий, необходимых для получения ответа на вопрос задачи, легче осуществлять с помощью рассматриваемых моделей. Например, модель задачи: «Сыну 15 лет. Отец на 25 лет старше сына. Мать на 5 лет младше отца. Сколько лет им вместе?» — будет выглядеть как на рисунке 3.
Второй блок включает данные о возрасте отца, определенном в результате первого действия, заданном возрасте матери (на 5 лет моложе отца) и способе его нахождения — вычитание: 40 — 5 = 35. Это второе действие.
Третий блок, помимо результата второго действия (возраст матери), включает данные первых двух блоков — возраст сына и отца и способ нахождения ответа.
Рассмотренные знаково-символические средства позволяют создавать модель структуры задачи, включающей объекты, характеризующие их величины, соответствующие им числовые значения (данные и искомые), и фиксировать или выводить действия, необходимые для ответа на вопрос задачи.
Таким образом, при переводе текста задачи на язык материки могут быть использованы схемы (модели) различной степени сложности: от простых с минимальным числом объектов и отношений до сложных. Необходимость в таких схемах выступает отчетливо, когда последовательность выполнения действий по решению задачи расходится с явной структурой задачи или эта структура сложна и открывает miJj гие и разные возможности решения.
Наряду с описанными выше способами в практике обучения широко используется табличный способ представление содержания задачи. Он чаще всего применяется для задач разнородными величинами, когда часть из них является переменными, связываемыми постоянной величиной. Это, как правило, задачи на «процессы».
При создании таблицы фактически реализуются те же этапы учебного моделирования, которые были указаны выше.
I. Анализ текста задачи.
1. Определение вида процесса: движение, работа, купля/продажа.
2. Выделение величин этого процесса и соответствующих им единиц измерения: движение — скорость, время, путь; работа — общий объем, время выполнения, объем работы за определенное время; купля/продажа — цена, стоимость, количество.
П. Составление таблицы.
1. В столбце фиксируются значения величин; количество величин определяет количество столбцов.
2. В строках фиксируются участники (объекты) и этапы процесса; количество строк определяется числом участников и этапов процесса (например, первая покупка, вторая покупка, периоды работы и т. п.).
3. Вычерчивание таблицы, в которой записывается название столбцов и строк.
III. Работа с таблицей.
На основе данных, представленных в таблице, выделяются функциональные отношения между величинами (прямая или обратная зависимость); между частными и общими значениями величин; изолированное или совместное действие участников (помогают друг другу или противодействуют); время включения в процесс (одновременно или в разное).
Выявленные зависимости между величинами позволяя выстроить последовательность действий для решения задачи
При обучении решению задач с помощью таблицы желательно вначале использовать расширенный ее вариант, где, кроме величин, их характеристик, единиц измерения, указывается вид процесса и дается обозначение участников (объектов). В общем виде таблица может быть представлена следующим образом (табл. 10):
Дата добавления: 2018-05-31 ; просмотров: 1117 ; Мы поможем в написании вашей работы!
15 убийственных вопросов на собеседовании в Google
Google предпочитает набирать работников среди выпускников восьми частных американских вузов («Лиги плюща»): Браунского университета, Гарварда, Принстона, Пенсильванского университета, Дартмутского колледжа, Йельского университета, Колумбийского университета, Корнельского университета.
Представители компании не скрывают, что им важны оценки, полученные во время обучения, даже если соискателю уже за тридцать. Ну и последнее: Google ищет людей, которые хотят изменить мир.
Ниже приводятся 15 вопросов, которые вы могли бы услышать, придя на собеседование в офис Google.
1. Сколько шариков для гольфа поместится в школьный автобус?
Позиция: менеджер по продукции
Это один из вопросов, которые задают в компании, чтобы посмотреть, каким образом соискатель ищет решение проблемы. Один из соискателей нашел хороший ответ: «Я представил стандартный школьный автобус шириной 8 футов, высотой 6 футов и длиной 20 футов: это примерные размеры, основанные на моих наблюдениях во время долгого стояния в пробках позади школьного автобуса. Это значит 960 кубических футов, 1728 кубических дюймов в кубическом футе, а это значит около 1,6 миллиона кубических дюймов. Я подсчитал, что объем мяча для гольфа около 2,5 кубического дюйма (4/3 * pi * 0.85), так как радиус мяча — 0,85 дюйма. Разделив 1,6 миллиона на 2,5 кубического дюйма, получится 660 тыс. шаров для гольфа. Однако, учитывая сиденья в автобусе и прочие вещи, занимающие свободное место, а также сферическую форма мяча, я предположил, что между ними будет достаточно много свободного места. И я округлил значение до 500 тыс. шаров».
2. За какую сумму денег вы помоете все окна в Сиэтле?
Позиция: менеджер по продукции
Это один из тех вопросов, где надо призвать на помощь смекалку и дать самый простой ответ. Мы бы ответили: «10$ за окно».
3. В стране, где люди хотят, чтобы у них были только дети-мальчики, каждая семья продолжает рожать детей до тех пор, пока не родится мальчик. Если у них рождается девочка, они заводят еще одного ребенка. Если мальчик, они останавливаются. Каково соотношение мальчиков и девочек в такой стране?
Позиция: менеджер по продукции
Ответ на этот вопрос вызвал оживленные дискуссии, в результате мы пришли к следующему решению. Представьте, что есть 10 семей, у которых 10 детей: 5 девочек, 5 мальчиков (всего – 10). Далее 5 пар, у которых девочки, родят еще пятерых детей. Половина (2,5) будут девочками, половина (2,5) — мальчиками. Добавляем 2,5 мальчика к уже рожденным 5 и 2,5 девочки к имеющимся 5 (всего детей 15, из которых 7,5 – мальчики и 7,5 – девочки). Теперь 2,5 парам, у которых девочки, надо родить 2,5 ребенка. Половина (1,25) будут мальчиками и половина (1,25) – девочками. Добавляем 1,25 мальчика к уже имеющимся 7,5 и 1,25 девочку к тем 7,5. (Всего детей 17,5, из которых мальчиков 8,75 и девочек – 8,75.) И так далее, придерживаясь принципа 50/50.
4. Сколько настройщиков пианино во всем мире?
Позиция: менеджер по продукции
Мы бы ответили: «Столько, сколько требуется рынком. Предположим, что пианино надо настраивать раз в неделю и это занимает один час, а настройщик работает 8 часов в день в течение 5 дней в неделю. Тогда получается, что 40 пианино требуют еженедельной настройки. Наш ответ: один для каждых 40 пианино».
5. Почему крышка люка круглая?
Позиция: разработчик ПО
Ответ. Чтобы она не могла упасть внутрь люка при ее монтаже или демонтаже (прямоугольная крышка легко входит в корпус люка по диагонали).
6. Разработайте план эвакуации для Сан-Франциско.
Позиция: менеджер по продукции
Ответ. Опять здесь смотрят, как соискатель подходит к решению проблемы. Мы бы начали свой ответ с вопроса: «А какое бедствие запланировано на сегодня?»
7. Сколько раз за сутки стрелки часов совпадают в одном положении?
Позиция: менеджер по продукции
Ответ. 22 раза. Из WikiAnswers: 00:00, 1:05, 2:11, 3:16, 4:22, 5:27, 6:33, 7:38, 8:44, 9:49, 10:55, 12:00, 13:05, 14:11, 15:16, 16:22, 17:27, 18:33,19:38, 20:44, 21:49, 22:55
8. Объясните значение выражения Dead beef (дословно: мертвое мясо)
Позиция: разработчик ПО
Ответ. DEADBEEF — шестнадцатиричное значение, которое использовалось для дебаггинга во времена больших мейнфреймов, потому что этот маркер было очень легко найти в шестнадцатиричных дампах. Большинство людей с компьютерным образованием должны были видеть это как минимум на уроках изучения ассемблера, вот почему в Google ожидают, что разработчик ПО знает об этом. 0xDEADBEAF (dead beef) использовался системами IBM RS/6000, Mac OS на 32-битном процессоре PowerPC и Commodore Amiga в качестве волшебного значения для дебага. На Solaris от Sun Microsystem это обозначало свободную память ядра. На OpenVMS, работающей на процессорах Alpha, DEAD_BEEF можно увидеть, нажав CTRL-T.
9. Человек направил свой автомобиль на отель, но потерпел неудачу. Что случилось?
Позиция: разработчик ПО
Ответ. Он застрял на бордюре. (Неприятно, правда?)
10. Вам надо проверить, правильно ли записан и записан ли вообще ваш телефон у вашего приятеля Боба. Но вы не можете его спросить об этом прямо. Вам надо написать вопрос на бумажке и отдать Еве, которая отнесет ее Бобу, а потом принесет обратно ответ от него. Что вы должны написать на бумажке (прямой вопрос нельзя) так, чтобы Боб смог понять сообщение, а Ева не смогла бы узнать ваш номер телефона?
Позиция: разработчик ПО
Ответ. Поскольку вы всего лишь проверяете, попросите его позвонить в определенное время. Если он не сделает этого, значит, у него нет вашего номера. Слишком просто? Еще один вариант ответа: «В этом случае надо использовать контрольную сумму. Пусть Боб сложит все числа вашего номера и напишет на листе результат, затем передаст вам обратно».
11. Вы — капитан пиратского судна, и ваша команда собирается голосовать, как разделить награбленное золото. Если с вами согласится меньше половины пиратов, вы умрете. Как вы поделите золото так, чтобы получить хорошую часть добычи, но все же остаться в живых?
Позиция: технический менеджер
Ответ. Надо разделить награбленное поровну между 51% всей команды.
12. У вас есть 8 шаров одинакового размера. 7 из них одинакового веса, а один весит чуть больше остальных. Найдите мяч, который тяжелее остальных, используя весы, показывающие баланс, и только два взвешивания?
Позиция: менеджер по продукции
Ответ. Возьмите 6 из 8 мячей и положите по 3 на каждую сторону весов. Если тяжелый мяч не в этой группе шаров, у вас есть еще 2, которые надо положить на весы и решить задачу. Если тяжелый шар в первой группе из 6 шаров, берите 3, которые перевесили во время первого взвешивания. Из этих трех два положите на чаши весов. Если один перевесит, то вы его нашли. Если же они весят одинаково, то значит ваш мяч — тот, который вы отложили.
13. У вас есть 2 яйца и есть доступ на 100-этажное здание. Яйца могут быть либо очень крепкими, либо очень хрупкими, а это значит, что они могут разбиться, если упадут с первого этажа, либо не разбиться, даже если их скинуть с 100-го этажа. Оба яйца абсолютно одинаковые. Вам нужно выяснить, какой этаж этого здания будет самый высокий для сохранения целости яиц при падении с него. Вопрос: сколько попыток вам надо сделать, чтобы выяснить самый высокий этаж? И при этом вы можете разбить только два яйца.
Позиция: менеджер по продукции
Ответ: Наибольшее количество попыток – 14 раз. Вместо того чтобы разбивать этажи по 10, надо начать с 14-го, затем подняться еще на 13 этажей, затем на 12, затем на 11, затем 10, 9, 8, 7, 6, 5, 4, до тех пор пока не дойдете до 99-го. Если бы яйцо разбилось на 100-м этаже, получилось бы 12 попыток (или 11, если вы предположите, что яйцо разобьется на 100-м этаже). Предположим, для примера, что мы выяснили, что 49-й — самый высокий этаж, где яйцо не разбилось, тогда наши попытки: 14-й, 27-й, 39-й, 50-й (яйцо разбилось на 50-м этаже) плюс 40, 41, 42, 43, 44, 45, 46, 47, 48 и 49 этаж — всего 14 попыток.
14. Объясните, что такое база данных в трех предложениях, чтобы понял ваш 8-летний племянник
Позиция: менеджер по продукции
Ответ. Основная цель этого вопроса заключается в оценке способности соискателя объяснить сложную идею простыми словами. Вот наша попытка: «База данных — это машина, которая запоминает большое количество информации о разных вещах. Люди используют ее, чтобы вспомнить эту информацию, когда им нужно. Пошли поиграем».
15. Вас уменьшили до размеров 5-центовой монеты, и ваша масса была пропорционально уменьшена в соответствии с вашей плотностью. Вас бросили в пустой стакан блендера. Ножи начнут движение через 60 секунд. Что делать?
Позиция: менеджер по продукции
Ответ. Этот вопрос оценивает креативность соискателя. Мы бы попробовали сломать электромотор.