булево значение что это
Булевский тип
Содержание
Реализация
Булевый тип данных может быть реализован с использованием только одного бита, но обычно используется минимальная адресуемая ячейка памяти (байт) или машинное слово, как эффективная единица работы с регистрами и оперативной памятью.
Доступные операции
К этому типу данных применимы следующие операции:
Так же могут использоваться и другие операции булевой алгебры. Большинство языков программирования позволяют использовать булевый тип и в арифметических операциях, приводя его к численному типу согласно принятым в языке правилам приведения типов.
Применение
Традиционным применением булевого типа данных являются значения «да»/«нет» в отношении результата более сложных операций.
Все операции сравнения двух величин (равно, больше, меньше), операции вхождения элемента в множество и проверка на пересечение множеств возвращают в качестве результата булевый тип.
Реализация в различных языках программирования
Algol
Algol 60 имеет тип данных boolean и соответствующие операторы, установленные в спецификации Algol 60. Тип данных был сокращён до bool в ALGOL 68.
В языке программирования C, который не предоставлял булевых значений в C89 (но вводит в C99) вместо значений true/false было установлено сравнение значения с нулём. Для примера, код на C
Это было честно для типа данных целочисленное (integer); тем не менее бинарные значения чисел с плавающей запятой (floating-point) были приближёнными к выводимым на экран десятичным значениям и это давало ошибки при сравнении. Традиционно, целое содержало одну (или более) булевую переменную (одну на каждый разряд целого).
Python
Для других объектов результат рассчитывается через метод __nonzero__, который в идеале должен возвращать значения True/False.
Булевый тип приводится к следующим типам данных:
К другим типам данных булевый тип не приводится.
Pascal
Описание переменных
Операции
Арифметических нет. Операций отношений нет. Допустимы следующие логические операции: Not, And, Or, Xor Допустимые функции: Ord,Pred,Succ
Полезное
Смотреть что такое «Булевский тип» в других словарях:
булевский тип — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN boolean type … Справочник технического переводчика
Перечисляемый тип — (сокращённо перечисление, англ. enumeration, enumerated type) в программировании тип данных, чьё множество значений представляет собой ограниченный список идентификаторов. Содержание 1 Описание и использование 2 … Википедия
Примитивный тип — Примитивный (встроенный, базовый) тип тип данных, предоставляемый языком программирования как базовая встроенная единица языка. В зависимости от языка и его реализации, набор таких типов может сильно различаться. Он определяется… … Википедия
C++ — У этого термина существуют и другие значения, см. C. См. также: Си (язык программирования) C++ Семантика: мультипарадигмальный: объектно ориентированное, обобщённое, процедурное, метапрограммирование Тип исполнения: компилируемый Появился в … Википедия
С++ — См. также: Си (язык программирования) C++ Семантика: мультипарадигмальный: объектно ориентированное, обобщённое, процедурное, метапрограммирование Тип исполнения: компилируемый Появился в: 1985 г. Автор(ы): Бьёрн Страуструп … Википедия
C— — (читается как Cи минус минус), название для нескольких независимо развитых языков программирования. Цель этих языков состоит в том, чтобы заменить язык программирования C другим портируемым языком, который ближе привязан к компьютерным апп … Википедия
Объектный Си — Objective C Класс языка: объектно ориентированный, мультипарадигмальный: рефлексивно ориентированный Появился в: 1986 г. Автор(ы): Типизация данных: строгая полиморфная, статическая Основные реализации: Apple gcc Испытал … Википедия
Список дворянских родов Минской губернии — Титульная страница Алфавитного списка дворянских родов Минской губернии за 1903 г. Список дворянски … Википедия
Логический тип
Логический, булев (англ. Boolean или logical data type) тип данных — примитивный тип данных в информатике, которые могут принимать два возможных значения, иногда называемых правдой (true) и ложью (false). Присутствует в подавляющем большинстве языков программирования как самостоятельная сущность или реализуется через численный тип. В подавляющем большинстве языков за истину полагается единица, за ложь — ноль.
Название Boolean получило своё название в честь английского математика и логика Джорджа Буля, среди прочего, занимавшегося вопросами математической логики в середине 19 века.
Содержание
Реализация
Булев тип данных может быть реализован с использованием только одного бита, но обычно используется минимальная адресуемая ячейка памяти (байт) или машинное слово, как эффективная единица работы с регистрами и оперативной памятью.
Доступные операции
К этому типу данных применимы следующие операции:
Так же могут использоваться и другие операции булевой алгебры. Большинство языков программирования позволяют использовать булев тип и в арифметических операциях, приводя его к численному типу согласно принятым в языке правилам приведения типов.
Применение
Традиционным применением булева типа данных являются значения «да»/«нет» в отношении результата более сложных операций.
Все операции сравнения двух величин (равно, больше, меньше), операции вхождения элемента в множество и проверка на пересечение множеств возвращают в качестве результата булев тип.
Реализация в различных языках программирования
Algol
Algol 60 имеет тип данных boolean и соответствующие операторы, установленные в спецификации Algol 60. Тип данных был сокращён до bool в ALGOL 68.
В языке программирования C, который не предоставлял булевых значений в C89 (но вводит в C99) вместо значений true/false было установлено сравнение значения с нулём. Для примера, код
Это было честно для целочисленного типа данных (integer); тем не менее, бинарные значения чисел с плавающей запятой (floating-point) были приближёнными к выводимым на экран десятичным значениям и это давало ошибки при сравнении. Традиционно, целое содержало одну (или более) булеву переменную (одну на каждый разряд целого).
Python
Для других объектов результат рассчитывается через метод __nonzero__, который в идеале должен возвращать значения True/False.
Булев тип приводится к следующим типам данных:
К другим типам данных булев тип не приводится.
В Python 2.6 есть интересная особенность — можно переопределить значение True на False и наоборот, написав всего-лишь
или, вариант для всей области видимости
что может привести к весьма неожиданному поведению интерпретатора или IDLE. В python 3 данная возможность была ликвидирована — True и False считаются зарезервированными, как и слово None.
Pascal
Арифметических операций нет, но допустимы логические операции: Not, And, Or, Xor, операции отношения =, <> и функции Ord, Pred, Succ.
См. также
Логический • Низший тип • Коллекция • Перечисляемый тип • Исключение • First-class function • Opaque data type • Recursive data type • Семафор • Поток • Высший тип • Type class • Unit type • Void
Абстрактный тип данных • Структура данных • Интерфейс • Kind (type theory) • Примитивный тип • Subtyping • Шаблоны C++ • Конструктор типа • Parametric polymorphism
Полезное
Смотреть что такое «Логический тип» в других словарях:
логический тип данных — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN logical data type … Справочник технического переводчика
РАЦИОНАЛЬНО-ЛОГИЧЕСКИЙ ТИП ЛИЧНОСТИ — РАЦИОНАЛЬНО ЛОГИЧЕСКИЙ (от лат. rationalis – разумно обоснованный, целесообразный) ТИП ЛИЧНОСТИ. Личность, для которой характерно предпочтение некоммуникативного способа изучения языка: учащиеся этого типа склонны к анализу языкового материала, к … Новый словарь методических терминов и понятий (теория и практика обучения языкам)
Тип данных — (встречается также термин вид данных) фундаментальное понятие теории программирования. Тип данных определяет множество значений, набор операций, которые можно применять к таким значениям и, возможно, способ реализации хранения значений и… … Википедия
ЛОГИЧЕСКИЙ МЕТОД ИССЛЕДОВАНИЯ — метод воспроизведения в мышлении сложного развивающегося (развивавшегося в прошлом) объекта (органического целого, системы) в форме историч. теории. Наряду с историч. методом, воспроизводящим тот же объект в виде истории системы, Л. м. и.… … Философская энциклопедия
Тип — (греч. отпечаток, модель). Проблема Т. и типизации не является специфической проблемой литературоведения. Она имеет место в науках разных областей знания. Вопрос о Т. и типизации в литературе характеризуется своими особенностями, к рые… … Литературная энциклопедия
логический закон — ЛОГИЧЕСКИЙ ЗАКОН общее название законов, образующих основу логической дедукции. Понятие о Л. з. восходит к древнегреч. понятию о логосе как о предпосылке объективной («природной») правильности рассуждений. Собственно логическое содержание … Энциклопедия эпистемологии и философии науки
тип — 2.2 тип: Лампы, имеющие одинаковые световые и электрические параметры, независимо от типа цоколя. Источник: ГОСТ Р МЭК 60968 99: Лампы со встроенными пускорегулирующими аппаратами для общего освещения. Требования безопасности … Словарь-справочник терминов нормативно-технической документации
тип данных — 2.35 тип данных (data type): Поименованная совокупность данных с общими статическими и динамическими свойствами, устанавливаемыми формализованными требованиями к данным рассматриваемого типа. Источник: ГОСТ Р ИСО/МЭК ТО 10032 2007: Эталонная… … Словарь-справочник терминов нормативно-технической документации
Тип Boolean, логические операторы и операторы сравнения
Логический тип Boolean в JavaScript представляет одно из двух значений: true (истина) или false (ложь).
Значения Boolean
В программировании очень часто бывают ситуации, когда требуется тип данных, который может принимать одно значение из двух, вроде
Именно для этих случаев в JavaScript существует логический тип данных Boolean, который может принимать только значение true (истина) или false (ложь).
Функция Boolean()
Чтобы определить, является ли выражение (или переменная) истиной (возвращает значение true), можно воспользоваться функцией Boolean():
Или можно сделать еще проще:
Все имеет «значение» True или False
Любое значение отличное от 0 имеет логическое значение true.
Логическое значение 0 (ноль) — false.
Логическое значение «» (пустая строка) — false.
Логическое значение undefined — false.
Логическое значение null — false.
Логическое значение false — false.
Логическое значение NaN — false.
Значения типа Boolean могут быть объектами
Обычно, логические значения типа Boolean определяются примитивными литералами:
Однако, в JavaScript при помощи ключевого слова new логические значения также можно определить и как объекты:
Тем не менее, не определяйте значения типа Boolean как объекты. Это замедляет скорость выполнения скрипта. Кроме этого, ключевое слово new в данном случае усложняет код и может привести к неожиданным результатам:
При использовании оператора сравнения ==, одинаковые значения типа Boolean равны:
Однако, при использовании оператора сравнения ===, одинаковые значения типа Boolean не будут равными, потому что оператор === ожидает совпадения как по значению, так и по типу.
Или еще хуже. Объекты не сравниваются:
Обратите внимание на разницу между (x==y) и (x===y).
Сравнение двух объектов JavaScript всегда возвращает ложь (false).
Логические операторы и операторы сравнения
Логические операторы и операторы сравнения используются для проверки выражений и переменных на соответствие какому-либо условию.
Значения типа Boolean лежат в основе всех сравнений и условий в JavaScript.
Операторы сравнения
Операторы сравнения используются в логических выражениях для определения совпадения или различия между переменными или значениями.
Предположим, что у нас есть x = 5. Следующая таблица объясняет операторы сравнения:
Условный (тернарный) оператор
В JavaScript есть особый условный оператор, который присваивает переменной значение в зависимости от заданного условия.
имя_переменной= (условие) ?значение1:значение2
В данном примере если в переменной age значение меньше 18, то переменной voteable будет присвоена строка «Слишком молод», в обратном случае переменной voteable будет присвоена строка «Возраст подходит».
Сравнение разных типов
Сравнение данных разного типа может привести к неожиданным результатам.
При сравнении строки и числа JavaScript будет преобразовывать строку в числовое значение. Пустая строка преобразуется в 0. Не числовая строка преобразуется в значение NaN, которое всегда равно false.
| Выражение | Значение |
|---|---|
| 2 «John» | false |
| 2 == «John» | false |
| «2» «12» | true |
| «2» == «12» | false |
При сравнении двух строк значение строки «2» будет больше значения строки «12», потому что в алфавитной последовательности 1 меньше 2.
Чтобы обезопасить результаты сравнения, переменные следует привести к надлежащему типу:
Булево выражение
В большинстве языков программирования среднего и высокого уровня определён набор встроенных операций сравнения позволяющих строить «простые» логические выражения. Самыми распространёнными являются:
В свою очередь, над логическими выражениями возможны операции результатом которых так же являются «истина» и «ложь» (см. логическая операция). Логические выражения построенные при помощи этих операций и содержащие несколько операций сравнения называются «сложными».
| Операция | Си | Паскаль |
|---|---|---|
| Или (дизъюнкция) | || | or |
| И (конъюнкция) | && | and |
| Отрицание | ! | not |
Примеры сложных логических выражений:
| Язык | Выражение | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| си | !A && (B || C) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| паскаль | not A and (B or C) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| си | A > 3 && B 3) and (B См. такжеПолезноеСмотреть что такое «Булево выражение» в других словарях:булево выражение — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Булево выражение Математическое выражение, в котором все переменные имеют значения либо 0 либо 1. [http://www.rfcmd.ru/glossword/1.8/index.php?a=index … Справочник технического переводчика булево выражение — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Булево выражение Математическое выражение, в котором все переменные имеют значения либо 0 либо 1. [http://www.rfcmd.ru/glossword/1.8/index.php?a=index … Справочник технического переводчика АЛГЕБРА ЛОГИКИ — система алгебраич. методов решения логич. задач, а также совокупность задач, решаемых такими методами. А. л. в узком смысле слова алгебраич. (табличное, матричное) построение классич. логики высказываний, в котором рассматриваются… … Философская энциклопедия Определение булевой функцииСодержаниеОсновные сведения [ править ]
Практически все булевы функции малых арностей ( [math]0, 1, 2[/math] и [math]3[/math] ) сложились исторически и имеют конкретные имена. Если значение функции не зависит от одной из переменных (то есть строго говоря для любых двух булевых векторов, отличающихся лишь в значении этой переменной, значение функции на них совпадает), то эта переменная называется фиктивной (англ. dummy variable). Нульарные функции [ править ]Унарные функции [ править ]Таблица значений булевых функций от одной переменной:
Названия булевых функций от одной переменной:
Бинарные функции [ править ]Таблица значений булевых функций от двух переменных:
Названия булевых функций от двух переменных:
Тернарные функции [ править ]
Названия булевых функций трех переменных:
Представление функции формулой [ править ]Тождественность и двойственность [ править ]
Тождественность функций f и g можно записать, например, так: Просмотрев таблицы истинности булевых функций, легко получить такие тождества:
А проверка таблиц, построенных для некоторых суперпозиций, даст следующие результаты:
[math]x \land (y\lor z)=(x \land y)\lor (x \land z)[/math] Если в булевом тождестве заменить каждую функцию на двойственную ей, снова получится верное тождество. В приведённых выше формулах легко найти двойственные друг другу пары. Суперпозиции [ править ]
Множество всех возможных не эквивалентных друг другу суперпозиций данного множества функций образует замыкание данного множества функций. Полнота системы, критерий Поста [ править ]
Американский математик Эмиль Пост [1] сформулировал необходимое и достаточное условие полноты системы булевых функций. Для этого он ввел в рассмотрение следующие замкнутые классы булевых функций: Представление булевых функций [ править ]Положительные ответы на эти и другие вопросы существенно увеличивают прикладное значение выбранной системы функций. Дизъюнктивная нормальная форма (ДНФ) [ править ]
Любая булева формула благодаря использованию закона двойного отрицания, закона де Моргана и закона дистрибутивности может быть записана в ДНФ. Конъюнктивная нормальная форма (КНФ) [ править ]
Любая булева формула с помощью использования закона двойного отрицания, закона де Моргана и закона дистрибутивности может быть записана в КНФ. [math]f(x,y,z) = (x \lor y) \land (y \lor \neg [math]f(x,y,z,t) = (x \lor t) \land (y \lor \neg [math]f(x,y,z,t,m) = (x \lor m \lor \neg Полином Жегалкина [ править ]Полином Жегалкина имеет следующий вид: [math]P = a_ <000\ldots000>\oplus a_ <100\ldots0>x_1 \oplus a_ <010\ldots0>x_2 \oplus \ldots \oplus a_ <00\ldots01>x_n \oplus a_ <110\ldots0>x_1 x_2 \oplus \ldots \oplus a_ <00\ldots011>x_ [math]f(x_1,x_2) = 1 \oplus x_1 \oplus x_1 x_2 [/math] [math]f(x_1,x_2,x_3) = x_1 \oplus x_1 x_2 \oplus x_2 x_3 [/math] [math]f(x_1,x_2,x_3,x_4) = 1 \oplus x_1 \oplus x_4 \oplus x_1 x_2 \oplus x_1 x_4 \oplus x_2 x_4 \oplus x_1 x_2 x_4 [/math] Тождественные функции. Выражение функций друг через друга [ править ]
Приведение тождественной функции есть выражение булевой функции через другие. Запись булевой функции в ДНФ, КНФ, а также выражение с помощью полинома Жегалкина — способы выражения одних булевых функций через другие. [math] x \oplus y = \left ( x \land \lnot y \right ) \lor \left ( \lnot x \land y \right ) = \left ( x \lor \lnot y \right ) \land \left ( \lnot x \lor y \right )[/math] [math] x \downarrow y = \lnot \left ( x \lor y \right) = \lnot x \land \lnot y[/math] [math]\langle x, y, z \rangle = \left ( x \land y \right ) \lor \left ( y \land z \right ) \lor \left ( x \land z \right ) = \left ( x \lor y \right ) \land \left ( y \lor z \right ) \land \left ( x \lor z \right )[/math] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Подстановка одной функции в другую [ править ]
Допускается также не только подстановка одной функции в другую, но и подстановка функции в саму себя.
Отождествление переменных [ править ]
| Пример: |
| [math] f(a,b) = a \vee b [/math] — исходная функция [math] h(a) = a \vee a [/math] — функция с отождествленными первым и вторым аргументами Очевидно, в данном примере мы получили функцию [math]P_<1>[/math] — проектор единственного аргумента. |
Схемы из функциональных элементов [ править ]
1. вершины, в которые не входят ребра, называются входами схемы, и каждая из них помечена некоторой переменной (разным вершинам соответствуют разные переменные);
Отождествление переменных осуществляется при помощи ветвления проводников.
Чтобы осуществить подстановку одной функции в другую нужно выход логического элемента, который реализует первую функцию, направить на вход логического элемента, который реализует вторую функцию.
Некоторые логические элементы:
| И | ИЛИ | НЕ | Штрих Шеффера | Стрелка Пирса |
|---|---|---|---|---|
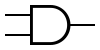 | 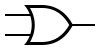 | 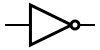 |  | 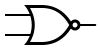 |
Стандартный базис [ править ]
[math] x \leftrightarrow y = \left ( x \rightarrow y \right ) \land \left ( y \rightarrow x \right ) [/math]
[math] x \rightarrow y = \lnot x \lor y [/math]
[math] 0 = x \land \lnot x [/math]
Функции [math] \mid \ и \downarrow[/math] являются отрицаниями функций [math] \land \ и \ \lor[/math] соответственно.
[math] x \mid y = \lnot \left ( x \land y \right )[/math]
[math] x \downarrow y = \lnot \left ( x \lor y \right )[/math]
Тождественность функций можно доказать с помощью таблицы истинности.
[math]x \leftarrow y = \lnot x \rightarrow \lnot y = x \lor \lnot y [/math]
Полнота стандартного базиса [ править ]
[math] x \land y = \lnot \left (\lnot x \lor \lnot y \right ) [/math]
[math] x \lor y = \lnot \left (\lnot x \land \lnot y \right ) [/math]
Следовательно, стандартный базис является избыточным, в то время как безызбыточными являются подмножества системы:
Теоремы о числе функций в базисе [ править ]
Значит, так как [math]X[/math] — безызбыточный базис, а система [math]\
Приведём примеры базисов для каждого [math]k[/math] :
[math]k = 1 \Rightarrow X = \< \downarrow \>[/math] ;
[math]k = 2 \Rightarrow X = \< \lnot, \land \>[/math] ;
Докажем, что последняя система является базисом: