булева алгебра для чего
Булева алгебра. Часть 1. Немного истории
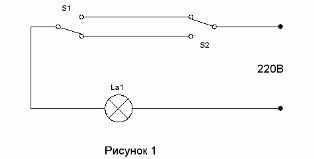
Схема, позволяющая двумя выключателями лампочку в коридоре включить при входе в коридор и выключить, войдя в комнату известна очень давно (cм. Коридорная схема управления освещением). Она показана на рисунке 1.
Задача №1. Более сложная. Составить схему, позволяющую включать и выключать свет в вашей комнате любым из 3 различных выключателей. Выключатели расположены у входа в комнату, над постелью и у письменного стола.
Задача № 2.
В спортивном комитете, например заводском, собралось 5 судей.
Каждый из них должен голосовать за принятие различных решений. Решение принимается большинством голосов, но только при том дополнительном условии, что за него голосует председатель комитета.
Задача №3. Практически такое маловероятно, но в качестве сложной учебной задачи вполне подойдет.
В большой шестиугольной комнате на каждой стене установлено по одному переключателю. Постройте такую схему, чтобы в любой момент можно было включать или выключать свет в комнате поворотом одного (любого) переключателя.
После того, как вы безрезультатно просидите над задачами три-четыре дня, отложите их временно в сторону. И займитесь алгеброй Буля. Именно алгебра Буля, или, как ее еще называют, булева алгебра, алгебра релейных схем, поможет вам решить составленные задачи.
Что же такое алгебра Буля?
Как ни странно, несмотря на то, что пять лет в школе изучают алгебру, многие ученики, а впоследствии и взрослые, не смогут ответить на вопрос, а что такое алгебра? Алгебра — это наука, которая изучает множества некоторых элементов и действия над ними.
В школьном курсе алгебры такими элементами являются числа. Числа можно обозначать не цифрами, а буквами, с этим все знакомы. На первых уроках алгебры это всегда затрудняет многих учеников. Вспомните, как трудно было вначале привыкнуть вместо цифр складывать буквы, решая ничего не говорящие уравнения.
Наверное, каждый из нас тогда задавал себе вопрос: «Для чего нужно вводить буквы вместо цифр и, нужно ли это вообще?». И только позднее вы убедились, какие преимущества при решении задач дает алгебра в сравнении с арифметикой.
Алгебра применяется во многих точных науках. Это физика, механика, сопромат, электричество. Закон Ома есть не что иное, как алгебраическое уравнение: достаточно вместо букв подставить их числовые значения, чтобы узнать какой ток будет протекать в нагрузке, или какое сопротивление имеет участок цепи.
Так вы познакомились с алгеброй чисел, или с элементарной алгеброй. Основная и почти единственная задача — получить ответ на вопрос: «Чему равняется X? Сколько?»
В старших классах школы изучают начала векторной алгебры. Эта алгебра принципиально отличается от элементарной алгебры. В ней совершено другая природа изучаемого множества и другие правила действий. Решая векторное уравнение, получаем в ответе вектор, который не является обычным числом, отвечающим на вопрос «Сколько?»
Формулы векторной алгебры во многом отличны от формул элементарной алгебры. Например, и в элементарной алгебре и в векторной имеется операция сложения. Но выполняется она совершенно по-разному. Сложение чисел выполняется совсем не так, как сложение векторов.
Существуют и другие алгебры: линейная алгебра, алгебра структур, алгебра колец, алгебра логики, или, что то же самое, алгебра Буля. На школьных уроках вы, наверное, не слышали имени Джорджа Буля — зато всем известно имя одной из его талантливых дочерей Этель Войнич (1864 – 1960). Она написала роман «Овод», где рассказывается о борьбе за свои права итальянских карбонариев.

Рассказывая ученикам о трудностях, с которыми ученые неизбежно сталкивались в поиске истины, учитель любил повторять одну восточную мудрость: даже персидский трон не может принести человеку столько наслаждений, как самое маленькое научное открытие. Буль никогда не терял надежды, что когда-нибудь и его ученики сделают настоящее открытие.
Диапазон научных интересов Буля был очень широк: в равной степени его интересовали математика и логика — наука о законах и формах мышления. В те времена логика считалась гуманитарной наукой, и многих, кто знал Джорджа Буля, удивляло, как в одном человеке могли уживаться точные методы познания, присущие математике, и чисто описательные методы логики.
Но ученому захотелось сделать науку о законах и формах мышления такой же строгой, как и любая из естественных наук, скажем математика и физика. Для этого Буль стал обозначать буквами не числа, как это делается в обычной алгебре, а высказывания и показал, что такими уравнениями, очень схожими с алгебраическими, можно решать вопросы об истинности и ложности высказываний, сделанных человеком. Так возникла алгебра Буля.
Но еще задолго до Джорджа Буля немецкий математик и философ Готфрид Лейбниц (1646—1716) впервые высказал идею о создании науки, которая обозначит все понятия обычной разговорной речи символами и установит некоторую новую алгебру для соединения этих символов.
После создания такой науки, по мнению Лейбница, ученые и философы перестанут спорить и перекрикивать друг друга, выясняя истину, а возьмут в руки карандаш и спокойно скажут: «Давайте-ка вычислять!»

Новым в алгебре Буля является то, что элементы множества, которые в ней изучаются, являются не числами, а высказываниями. Если при решении обычных алгебраических уравнений определяется, какому числу равняется неизвестное X, школьная алгебра ищет ответ на вопрос: «Сколько?»
Алгебра логики ищет ответ на вопрос: «Верно ли то или другое высказывание, обозначенное буквой X?»
Смысл и содержание высказывания здесь не играют никакой роли. Каждое высказывание может быть только или истинным, или ложным. Оно не может быть наполовину истинным и наполовину ложным. В качестве примера можно вспомнить метание жребия при помощи монеты.
Там рассматриваются только два состояния монеты — орел или решка. По договоренности сторон орел это ДА, а решка это НЕТ. Никакие другие промежуточные положения в теории вероятностей не учитываются, хотя они и возможны. Подброшенная монета может упасть на ребро, докатиться по полу до ножки стула или стола и так и остаться в вертикальном положении, а то и вообще провалиться в широкую щель в полу. (По аналогии с электрическими схемами две последних ситуации можно рассматривать как неисправность в виде обгоревшего контакта). Но в те далекие времена булева алгебра, увы, широкого распространения не получила.

С помощью алгебры Буля можно очень просто составить электрическую схему автомата, работающего на реле. Для этого, оказывается, нужно только точно знать, что должен делать автомат, то есть нужно иметь алгоритм его работы. Так была заложена основа теории цифровых машин, действующих по принципу ДА или НЕТ.
Такова вкратце история булевой алгебры. В следующих статьях мы рассмотрим ее основные законы, примеры контактных схем реализующие эти законы. Рассмотрим решение тех задач, которые были приведены в начале статьи.
Булевы алгебры и полукольца
Теория булевых алгебр является классическим разделом дискретной математики. Булевы алгебры возникли в трудах английского математика Дж. Буля в 50-х годах XIX века как аппарат логики. При этом элементы булевой алгебры трактовались как высказывания, а операциями являлись дизъюнкция, конъюнкция и отрицание.
Существуют различные подходы к определению булевой алгебры. Мы определим булеву алгебру как частный случай идемпотентного полукольца.
Определение 3.3. Полукольцо называют симметричным (или взаимным), если оно идемпотентно и в нем выполнены следующие тождества:
Запишем полностью все аксиомы (основные тождества) симметричного полукольца, объединяя двойственные аксиомы в пары (табл. 3.3).
Таким образом, справедлив принцип двойственности для симметричных полуколец: любое тождество в симметричном полукольце остается верным, если в нем операцию сложения заменить операцией умножения и наоборот, а единицу заменить нулем и наоборот.
Пример 3.8. а. Полукольцо (см. пример 3.2) симметричное.
в. Полукольцо (см. пример 3.3,б) симметрично в силу известных свойств операций пересечения и объединения множеств.
г. Полукольцо (см. пример 3.3,в) не является симметричным.
д. Полукольцо (см. пример З.З,г) симметрично.
Действительно, для любых двух натуральных чисел и верно представление
Свойства симметричного полукольца
Рассмотрим некоторые свойства симметричного полукольца, вытекающие из его аксиом.
Свойство 3.1. Для любых элементов симметричного полукольца выполняются равенства
Равенства, приведенные в формулировке свойства 3.1, называют тождествами поглощения.
Свойство 3.3. В симметричном полукольце произведение есть точная нижняя грань последовательности
Таким образом, в симметричном полукольце единица (1) является наибольшим элементом.
Запишем аксиомы булевой алгебры в виде табл. 3.4, объединяя «двойственные пары» (как это мы уже сделали, записывая аксиомы симметричного идемпотентного полукольца).
Свойства булевых алгебр
Свойство 3.5 (единственность дополнения). В булевой алгебре для любого его дополнение единственное.
С учетом свойств дополнения преобразуем последнее выражение следующим образом:
Свойство 3.6 («симметричность» операции дополнения). В булевой алгебре выполняется тождество
Свойство 3.7. В булевой алгебре верны следующие тождества:
В силу свойств 3.5 и 3.6 для доказательства первого закона достаточно показать, что
Преобразуя выражения в левых частях, получаем
Первое тождество доказано. Второе тождество следует из принципа двойственности.
Тождества (3.31) называют законами де Моргана для булевых алгебр.
Единственность дополнения означает, что в булевой алгебре возникает унарная операция — переход от элемента к его дополнению. Эту операцию можно ввести в сигнатуру алгебры, т.е. рассматривать булеву алгебру как алгебру вида
с двумя бинарными, одной унарной и двумя нульарными операциями, такую, что:
Дополнение в булевой алгебре называют булевым дополнением, а все операции булевой алгебры — булевыми операциями.
Примеры булевых алгебр
Рассмотрим теперь некоторые примеры булевых алгебр.
Итак, булевы операции над булевыми векторами выполняются покомпонетно — так же, как сложение векторов или умножение вектора на число в линейной алгебре. Отношение порядка здесь определено также покомпонентно, т.е. для произвольных
Пример 3.12. Полукольцо (см. пример 3.3.б) — булева алгебра, в которой все булевы операции суть не что иное, как обычные теоретико-множественные операции, т.е. булево объединение есть обычное объединение множеств, булево пересечение — пересечение множеств, булево дополнение — дополнение множества.
Теория булевых алгебр имеет многочисленные приложения: в математической логике, в теории вероятностей. Она позволяет, в частности, рассматривать с единой точки зрения операции над множествами, над высказываниями, над случайными событиями.
Булева алгебра
Что такое булева алгебра?
Булева алгебра – это раздел математики, который занимается операциями с логическими значениями и включает двоичные переменные. Булева алгебра берет свое начало в книге математика Джорджа Буля 1854 года.
Отличительной чертой булевой алгебры является то, что она занимается только изучением двоичных переменных. Чаще всего логические переменные представлены с возможными значениями 1 («истина») или 0 («ложь»). Переменные также могут иметь более сложные интерпретации, например, в теории множеств. Булева алгебра также известна как бинарная алгебра.
Ключевые выводы
Понимание булевой алгебры
Булева алгебра отличается от элементарной алгебры, поскольку последняя имеет дело с числовыми операциями, а первая имеет дело с логическими операциями. Элементарная алгебра выражается с помощью основных математических функций, таких как сложение, вычитание, умножение и деление, тогда как булева алгебра имеет дело с конъюнкцией, дизъюнкцией и отрицанием.
Понятие булевой алгебры было впервые введено Джорджем Булем в его книге «Математический анализ логики» и далее расширено в его книге «Исследование законов мысли». Поскольку ее концепция была подробно описана, булевская алгебра в основном использовалась в языках программирования. Его математические цели используются в теории множеств и статистике.
Булева алгебра в финансах
Булева алгебра находит применение в финансах посредством математического моделирования рыночной деятельности. Например, исследованию цен на опционы на акции может помочь использование бинарного дерева для представления диапазона возможных результатов для базовой ценной бумаги. В этой биномиальной модели ценообразования опционов, где есть только два возможных результата, логическая переменная представляет увеличение или уменьшение цены ценной бумаги.
Этот тип моделирования необходим, потому что для американских опционов, которые могут быть исполнены в любое время, траектория цены ценной бумаги так же важна, как и ее окончательная цена. Модель ценообразования биномиальных опционов требует, чтобы траектория цены ценной бумаги была разбита на серию дискретных временных диапазонов.
Таким образом, модель ценообразования биномиальных опционов позволяет инвестору или трейдеру отслеживать изменение цены актива от одного периода к другому. Это позволяет им оценивать вариант на основе решений, принятых на разных этапах. Поскольку опцион в США может быть исполнен в любое время, это позволяет трейдеру определить, следует ли ему исполнять опцион или удерживать его в течение более длительного периода. Анализ биномиального дерева позволит трейдеру заранее увидеть, следует ли исполнять опцион. Если есть положительное значение, то опцион должен быть исполнен, если значение отрицательное, то трейдер должен удерживать позицию.
БУЛЕВА АЛГЕБРА
Смотреть что такое «БУЛЕВА АЛГЕБРА» в других словарях:
БУЛЕВА АЛГЕБРА — БУЛЕВА АЛГЕБРА см. Алгебра логики. Новая философская энциклопедия: В 4 тт. М.: Мысль. Под редакцией В. С. Стёпина. 2001 … Философская энциклопедия
Булева алгебра — раздел математической логики, изучающий высказывания и операции над ними. Наиболее известными операциями булевой алгебры являются: конъюнкция, дизъюнкция, импликация, эквивалентность, отрицание. По английски: Boolean algebra См. также: Логические … Финансовый словарь
БУЛЕВА АЛГЕБРА — Boolean algebra От Дж.Буль английский математик 1815 1864 Раздел математической логики, изучающий высказывания и операции над ними. Наиболее известными операциями булевой алгебры являются: конъюнкция, дизъюнкция, импликация, эквивалентность,… … Словарь бизнес-терминов
Булева алгебра — Эта статья об алгебраической системе. О разделе математической логики, изучающем высказывания и операции над ними, см. Алгебра логики. Булевой алгеброй[1][2][3] называется непустое множество A с двумя бинарными операциями (аналог конъюнкции),… … Википедия
булева алгебра — Boolean algebra statusas T sritis automatika atitikmenys: angl. Boolean algebra vok. Boolesche Algebra, f rus. булева алгебра, f pranc. algèbre de Boole, f ryšiai: sinonimas – Bulio algebra … Automatikos terminų žodynas
БУЛЕВА АЛГЕБРА — булева решетк а, частично упорядоченное множество специального вида. Б. а. наз. дистрибутивная решетка (дистрибутивная структура), имеющая наибольший элемент 1 единицу Б. а., наименьший элемент 0 нуль Б. а. и содержащая вместе с каждым своим… … Математическая энциклопедия
Булева алгебра — алгебра, в которой каждая переменная может принимать одно из двух значений: «истина» или «ложь». Операции над переменными в булевой алгебре называются логическими операциями. Правила выполнения логических операций удобны для преобразования… … Начала современного естествознания
БУЛЕВА АЛГЕБРА — Названная по имени ее создателя, английского математика Джорджа Буля, система операций с символами, которая использует алгебраические процедуры, но независимо от определенных математических интерпретаций. Булева логика, или калькуляция (как она… … Толковый словарь по психологии
Булева алгебра — (араб.) – система алгебраических операций с символами, названная в честь Д. Буля, одного из её создателей. Также называется калькуляцией (лат. calсulatio – счёт, подсчёт). Интересно, что Д. Буль рассматривал свою работу как представление основных … Энциклопедический словарь по психологии и педагогике
Основные понятия булевой алгебры
ОСНОВНЫЕ ПОНЯТИЯ БУЛЕВОЙ АЛГЕБРЫ
Булевы функции. Способы задания булевых функций
Определение 1.1. Булевыми значениями (или булевыми константами) называются два заранее выбранных разных символа. Эти два значения могут быть обозначены как угодно, лишь бы по – разному. Самые распространенные варианты: 0 и 1, F и T, «false» и «true», «ложь» и «истина», Л и И, «да» и «нет». При изучении булевых функций по традиции используют символы 0 и 1 [12].
Определение 1.2. Булевыми переменными называются переменные, которые могут принимать булевы значения. Иногда булевой величиной называют величину, которая является булевой переменной или константой [11].
Область математики, которая изучает различные преобразования булевых величин, называется алгеброй логики или булевой алгеброй. На практике булева алгебра применяется в математических построениях, в повседневных рассуждениях, в вычислительной технике и других областях человеческой деятельности. В случая использования булевых функций в логических построениях в математике булевы величины принимают значения «ложь» и «истина». Они определяют истинность или ложность некоторого высказывания, представленного математическим выражением. При повседневных рассуждениях булевы значения «ложь» и «истина» представляют оценку истинности или ложности высказывания, понимая под высказываниями фразы естественного языка, которые удовлетворяют строго определенному списку свойств. При применении булевых функций в вычислительной технике используют булевы значения 0 и 1. Они представляют собой состояние ячейки памяти объемом в 1 бит или наличие или отсутствие напряжения в электрической схеме. Алгебра логики позволяет строить сложные электронные узлы, элементы которых работают согласно этой математической теории. Для того чтобы некоторую величину можно было обозначать булевой переменной, должны выполняться следующие ограничения:
1. Величина должна принимать только два возможных состояния.
2. В любой момент времени величина не может принимать оба состояния одновременно.
3. В любой момент времени величина не может принимать ни одного состояния.
4. Если рассматриваются несколько таких величин, то допускается, чтобы каждая из них принимала одно из двух состояний независимо.
5. Не допускается применять одну пару состояний для одной величины, а для другой – другую [13].
Определение 1.3. Функция от n аргументов
называется булевой функцией, если каждому набору из множества всех наборов она ставит в соответствие число из множества <0,1>[14].
Задать функцию означает установить правило (закон), с помощью которого по данным значениям независимой переменной следует находить соответствующие им значения функции [24].
Способы задания булевых функций не отличаются от способов задания обычных функций анализа. К таковым способам задания стандартно относятся:
1) табличный, 2) графический, 3) аналитический, 4)словесный.
Довольно распространен, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством [2].
При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции [18].
Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента [4].
Определение 1.4. Графиком функции называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению [20].
Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами – наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом [24].
Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции [4].
Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.
Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью.
Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений [5].
Этот способ состоит в том, что функциональная зависимость выражается словами. Основными недостатками словесного способа задания функции являются невозможность вычисления значений функции при произвольном значении аргумента и отсутствие наглядности. Главное преимущество же заключается в возможности задания тех функций, которые не удается выразить аналитически [6].
1.2. Элементарные булевы функции
Среди булевых функций встречаются функции от одной и от двух переменных. Функции от одной переменой называются элементарными, а от двух переменных называются соответственно конъюнкцией, дизъюнкцией, суммой по модулю два, импликацией, эквивалентностью.
Определение 1.6. Дизъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции).
Правило вычисления: результат равен 0, если все операнды равны 0; во всех остальных случаях результат равен 1. Формула: [9].
Схемы из функциональных элементов
Определение 1.11. Схема из функциональных элементов в базисе <&,˅, ─>– есть помеченный ориентированный граф без контуров, удовлетворяющий следующим условиям.
Все вершины этого графа разбиваются на три непересекающихся подмножества так, что:
а) объединение непересекающихся подмножеств;
б) в каждую вершину из не входит ни одной дуги;
в) в каждую вершину из входит по одной дуге;
г) в каждую вершину из входят по две дуги.
2) Каждой вершине из приписана некоторая переменная причем разным вершинам приписаны разные переменные.
3) Каждой вершине из приписан символ – (отрицание функции х).
4) Каждой вершине из приписан один из символов
Выделенные вершины из называются выходами схемы.
Вершины из (в которые не входят дуги) называются входами схемы. Каждая вершина из (с приписанным ей символом ⌐) называется ивертором. Каждая вершина из с приписанным ей символом & называется конъюнктором, а каждая вершина из с приписанным ей символом ˅ называется дизъюнктором. Каждая вершина из или называется функциональным элементом [18: 48 – 49].
Конъюнктор выглядит следующим образом:
Дизъюнктор выглядит так:
Инвертор же выглядит следующим образом:
В схемах могут быть неисправности различных типов: константные и инверсные. Неисправности каждого из типов могут предполагаться либо на входах схемы, либо на входах элементов схемы. Константная неисправность типа (где или 1) на входе элемента означает, что на этот вход подается константа а (соответственно, значение на входе этого элемента всегда равно ). В общем случае значение а может быть своим у каждого неисправного элемента. В случае однотипных константных неисправностей значение предполагается одним и тем же у всех неисправных элементов [19].
В данной работе будут рассмотрены инверсные неисправности.
Инверсная неисправность на входе элемента означает, что на этот неисправный вход подается значение, противоположное значению, подаваемому на исправный вход.
Инверсная неисправность на выходе элемента означает, что значение на выходе неисправного элемента противоположно значению, полученному на выходе исправного элемента.
Рис.6
т.е. вид схемы S не меняется, а меняются лишь входы.
Для того чтобы выяснить реализует ли схема верную функцию или нет, используют проверяющие тесты.
Определение 1.12. Проверяющий тест – это множество наборов, на которых можно определить, исправна схема или нет. Если в схеме имеется одна неисправность, то такой тест называется единичным проверяющим тестом, если же в схеме присутствуют k – неисправностей, то тест называется полным проверяющим тестом [5].
Для того чтобы выяснить какую именно функцию неисправности реализует схема используют диагностические тесты.
Определение 1.13. Диагностический тест – это множество наборов, на которых можно определить, исправна схема или нет и какая именно функция неисправности реализуется на выходе неисправной схемы. Если в схеме имеется одна неисправность, то такой тест называется единичным диагностическим тестом, если же в схеме имеется более одной неисправности, применяется полный диагностический тест [26].
Во второй главе квалификационной работы были рассмотрены инверсные неисправности на входах схем. Для функции была получена одна функция неисправности. На множестве A = <(0,0,…,0)>и B = = <(0,0,…,0), (1,1,…,1)>полученная функция неисправности отлична от самой функции. Следовательно получены следующие выводы: множество А – минимальный единичный проверяющий тест, состоящий из одного набора, а множество В – единичный диагностический тест, содержащий не более двух наборов. Для подробного анализа рассмотрели нетривиальные функции:,